北京时间10月8日下午5点45分左右,2024年诺贝尔物理学奖颁奖,授予John J. Hopfield 和 Geoffrey E. Hinton,以表彰他们“通过人工神经网络实现机器学习的基础性发现和发明”。这是复杂系统、统计物理中的经典模型“伊辛模型”(Ising Model)及其扩展引发的又一次诺奖。文末附带集智俱乐部关于统计物理、神经网络、人工智能等方向的读书会、科普百科和文章等资料。
John Hopfield @The Nobel Prize in Physics 2024
John Hopfield 1954 年在斯沃斯莫尔学院获得学士学位,1958 年在康奈尔大学获得物理学博士学位。他在贝尔实验室理论组工作了两年,随后在加州大学伯克利分校(物理学)、普林斯顿大学(物理学)、加州理工学院(化学和生物学)任教。John Hopfield 1969 年获美国物理学会奥利弗・巴克利奖,1973 年当选美国国家科学院院士,2001 年获国际理论物理中心(ICTP)狄拉克奖章。
Geoffrey E. Hinton@The Nobel Prize in Physics 2024
Geoffrey Hinton,2018年图灵奖得主,被誉为”深度学习之父”。他在神经网络和机器学习领域的开创性工作,为人工智能的革命性进展奠定了基础。Hinton的反向传播算法和对比散度算法等贡献,极大地推动了深度学习技术的发展和应用,对语音识别、图像处理等领域产生了深远影响。他的研究不仅在学术界受到高度评价,也对工业界产生了重大影响,推动了谷歌、苹果等公司的技术进步。Hinton对AI伦理和潜在风险的深刻洞察,为确保技术负责任的发展提供了重要指导。他的持续研究和对教育的重视,不断激励着新一代研究者,推动着人工智能技术的创新和进步。
类Ising模型再获诺奖:
从Ising模型到人工神经网络
张江 | 作者
这次的诺贝尔物理学奖和复杂科学的关系十分密切,这主要体现在 Hopfield 提出的神经网络模型可以看作是复杂系统、统计物理中的经典模型——“伊辛模型”(Ising Model)的一种推广。伊辛模型很好地体现了复杂系统中普遍存在的有序与无序竞争。二维的伊辛模型可以看作是展现有序-无序临界相变现象(也称作混沌与秩序的边缘)的最小模型。
伊辛模型的一个通俗版本就是观点动力学模型:假设有一个村落,大家开始选村长,是张三还是李四?假设每个村民都会受周围四个邻居的影响,邻居选张三多,则该村民也倾向于投票张三。当然,每个村民也存在一定的个性,也就是说它可能会以一定的倾向不去顾及周围邻居的选择,而完全按照自己的意愿来投票。就这样,每一周期,每个村民就去看看周围邻居的选择,然后决定自己的投票。这样演化下去,村民的投票选择就会形成一定的动态。调整独立选择倾向性参数,会得到不同的动态结果。如果倾向性高,则系统演化会非常随机;如果倾向性低,则系统会演化到所有村民都只选择某一个选择上;存在一个临界的倾向性,系统展现出高度的复杂性:每个村民会对到底选张三还是李四而犹豫不决,反复改变。
图1. 二维的伊辛模型,每个小箭头就代表一名村民,向上代表选择张三,向下选择李四。每个村民受到上下左右四个邻居,以及是否倾向于自己的意愿选择的影响。
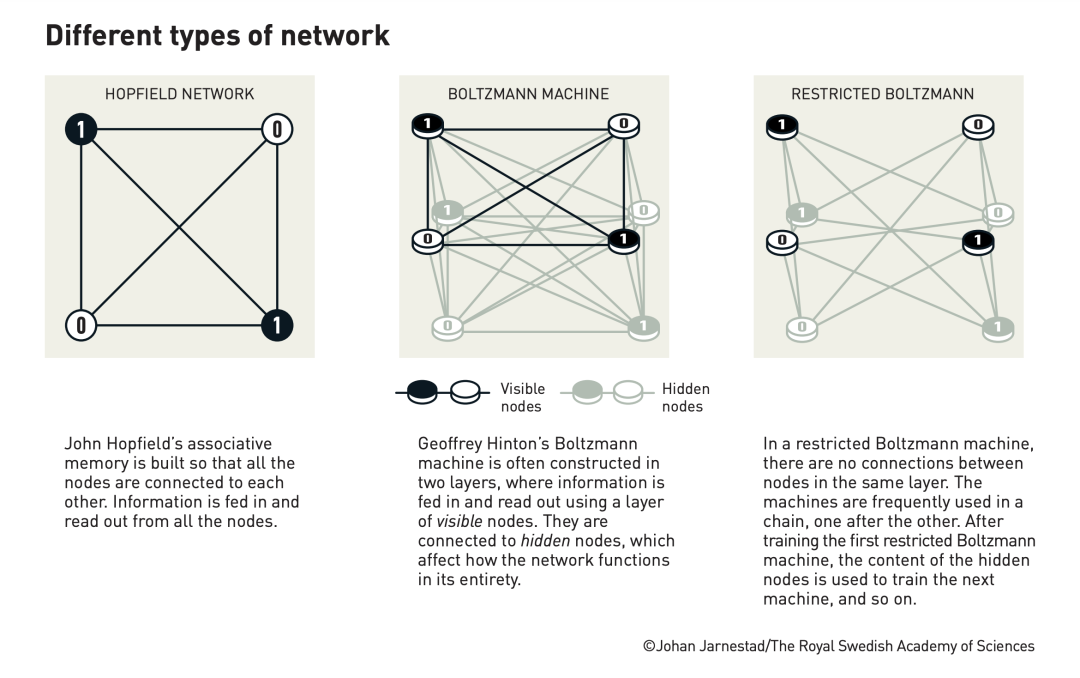
Hopfield 网络是对伊辛模型的扩展。首先,每个神经元就是一个村民,其次他们生活在高度发达的网络社会,因此每个神经元之间的链接是一个全连接的网络。
其次,村民之间的链接不再是一成不变的,而是会随着神经网络的训练过程而发生演变。训练的最终目标就是要让整个网络上各个神经元经过类似村民投票规则的演化所形成的最终状态能够满足一定的要求的分布形式,如上图左边黄色,右边绿色的分布,从而让网络具备一定的记忆能力。
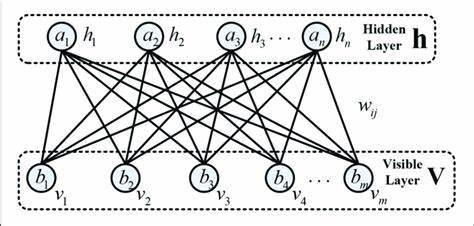
当然,这种网络还和今天常见的前馈类型的神经网络相差太远,于是,Hinton 就在 Hopfield 模型基础上做了扩展,得到一种能够区分输入和输出的二分网络,其中一部分接收输入数据,另一部分则起到记忆作用,这种网络称为“受限的玻尔兹曼机”(Restricted Boltzmann machine)。将多种这样的网络串联起来,还可以形成深度的网络,这也构成了第一个可以被称为“深度神经网络”的架构。
https://wiki.swarma.org/index.php/伊辛模型
-
从 Ising 模型到 Boltzmann 机,还有一篇很好的科普:
https://leovan.me/cn/2018/01/ising-hopfield-and-rbm/#:~:text=%E8%BF%9E%E7%BB%AD%E5%9E%8B%20Hopfie
今年的两位诺贝尔物理学奖获得者是 John Hopfield 和 Geoffrey Hinton,他们基于物理学工具提出的方法为机器学习的强大能力奠定了基础。John Hopfield 提出的联想记忆(associative memory),可以存储和重建数据(包括图像和其他类型的数据)中的模式。Geoffrey Hinton 发明了可以自主发现数据属性的方法,从而执行诸如识别图片中特定元素等任务。
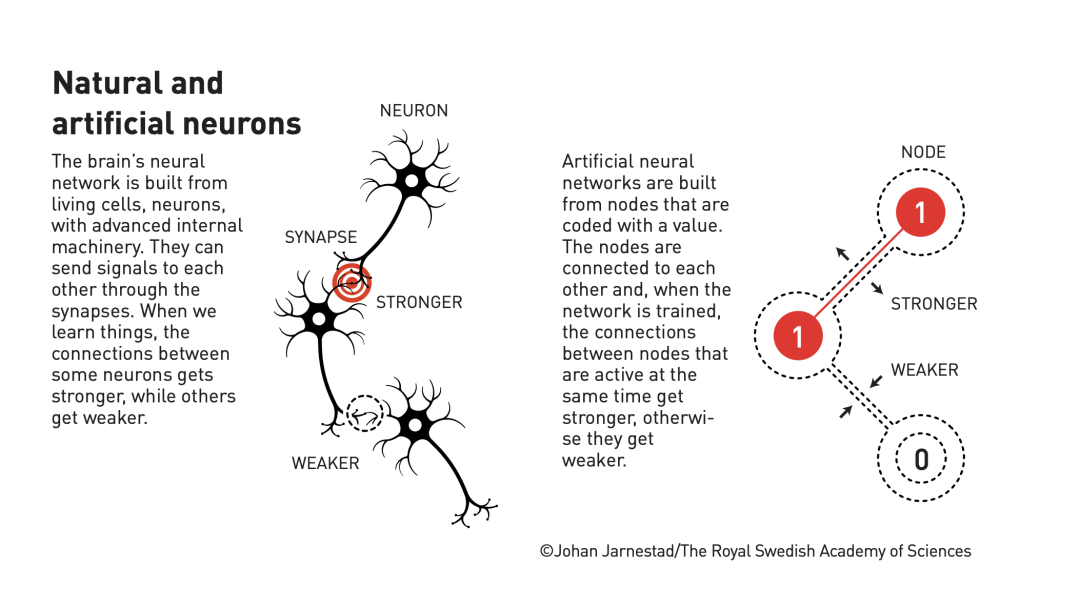
当我们谈论人工智能时,通常指的是使用人工神经网络的机器学习。这项技术最初受大脑结构的启发。在人工神经网络中,大脑的神经元由具有不同数值的节点表示。节点之间通过类似突触的连接相互影响,影响可以增强或减弱。通过对同时具有高数据的节点之间的连接进行加强等方式,可以对人工神经网络进行训练。今年的获奖者自上世纪80年代以来在人工神经网络领域开展了重要工作。
人工神经网络最初是受大脑神经元的启发
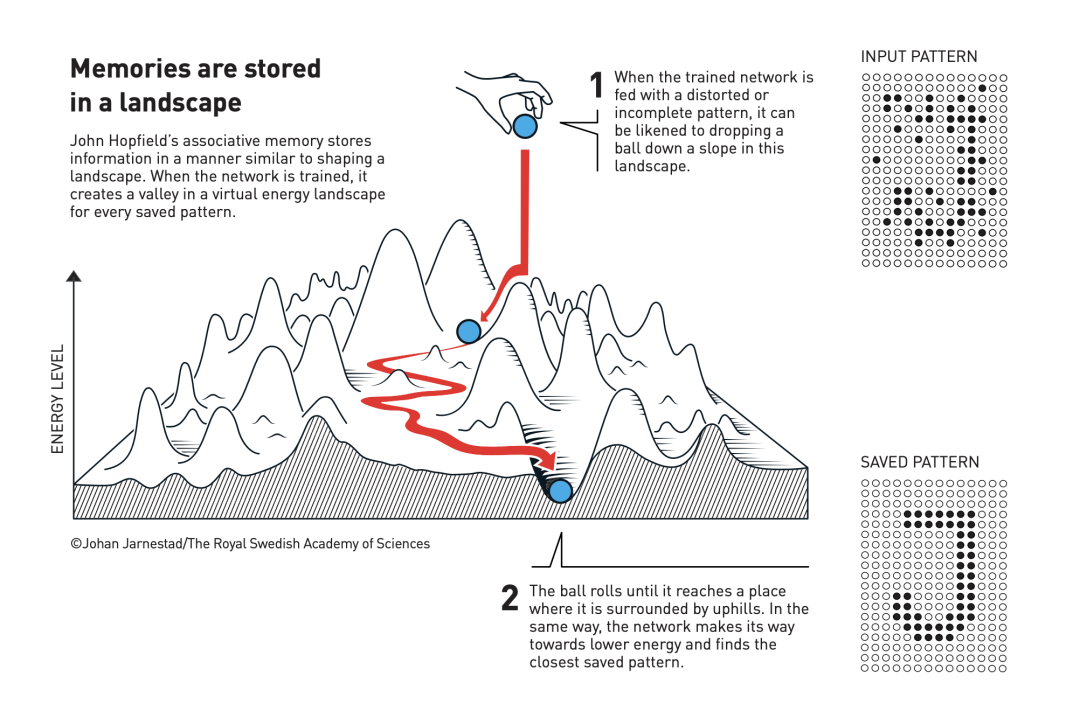
John Hopfield 发明的 Hopfield 网络,专门用于存储和重建模式。我们可以将节点想象为像素,整个 Hopfield 网络就对应一副图像。Hopfield 网络利用了物理学中描述材料特性的自旋方法(自旋是使每个原子成为微小磁铁的属性)。借鉴物理学中描述自旋系统能量的方式,可以对 Hopfield 网络作为一个整体进行描述,并通过寻找节点之间的连接值进行训练,从而保存具有较低能量的图像。当 Hopfield 网络接收到失真或不完整的图像时,它会按照一定的策略遍历节点并更新其值,从而降低网络的能量。这样,Hopfield 网络就能逐步从存储的图像中找到与输入图像最相似的图像。
John Hopfield 提出的联想记忆(associative memory)可以存储和重建数据中的模式。
Geoffrey Hinton 以 Hopfield 网络为基础发明了一种新的网络——玻尔兹曼机(Boltzmann machine)。玻尔兹曼机能够通过学习识别给定数据类型中具有特征的元素。Hinton 借助统计物理的工具——统计物理主要研究由大量粒子组成的系统的整体行为和性质——通过输入在运行过程中可能出现的示例对玻尔兹曼机进行训练。训练好的玻尔兹曼机可以用来对图像分类,或生成与训练示例的模式类似的新图像,Hinton 在此基础上进一步发展,开启了当前机器学习的爆炸性发展。
诺贝尔物理学委员会主席 Ellen Moons 表示:“获奖者的工作已经带来了巨大的益处。在物理学中,我们在开发具有特定属性的新材料等广泛的领域使用人工神经网络。”
相关资源推荐:
统计物理学不仅能解释热学现象,还能帮助我们理解从微观粒子到宏观宇宙的各个层级如何联系起来,复杂现象如何涌现。它通过研究大量粒子的集体行为,成功地将微观世界的随机性与宏观世界的确定性联系起来,为我们理解自然界提供了强大的工具,也为机器学习和人工智能领域的发展提供了重要推动力。
集智俱乐部联合纽约州立大学石溪分校教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学助理教授唐乾元,共同发起「非平衡统计物理」读书会,关注非平衡统计物理的前沿理论进展、生命和热力学、统计物理与机器学习交叉三个大的主题方向,涵盖热机优化问题、涨落相关的热力学、反常热力学现象、信息视角下的热力学、生命系统的景观和流理论、活性物质、生命系统、种群动力学、机器学习和人工智能等前沿话题。读书会计划从11月19日开始,每周二晚19:00-21:00进行。我们诚挚邀请相关领域的研究者分享的工作,也欢迎大家一起参与讨论交流!
统计物理方法是一座架起微观作用到宏观涌现的桥梁,2021年诺贝尔物理学奖得主帕里西在无序系统方面作出开创之举,他提出复本对称破缺方法解决自旋玻璃问题,这一方法也对神经网络等交叉学科产生深厚影响,激发未来对人工智能和人脑等复杂系统的进一步研究。本节课程介绍什么是自旋玻璃、自旋玻璃应用的几个经典例子、为什么需要空腔方法、空腔方法的基本思想和具体推导以及消息传递算法等内容,搭建从统计物理到神经网络重要的桥梁,帮助大家更好理解神经网络的基本原理。
![]()
课程详情:黄海平:神经网络的统计力学课程
集智学园最新AI课程,
张江教授亲授:第三代人工智能技术基础
——从可微分编程到因果推理
自1956年“人工智能”诞生于达特茅斯会议以来,已经经历了从早期的以符号推理为主体的第一代人工智能,和以深度神经网络、机器学习为主体的第二代人工智能。ChatGPT的横空出世、生成式AI的普及、AI for Science等新领域的突破,标志着第三代人工智能的呼之欲出。可微分编程、神经微分方程、自监督学习、生成式模型、Transformer、基于图网络的学习与推理、因果表征与因果推断,基于世界模型的强化学习……,所有这些脱胎于前两代人工智能的技术要素很有可能将构成第三代人工智能的理论与技术的基础。
本课程试图系统梳理从机器学习到大语言模型,从图神经网络到因果推理等一系列可能成为第三代人工智能基础的技术要素,为研究者或学生在生成式AI、大模型、AI for Science等相关领域的学习和研究工作奠定基础。
点击“阅读原文”,报名读书会