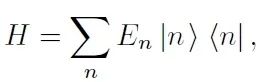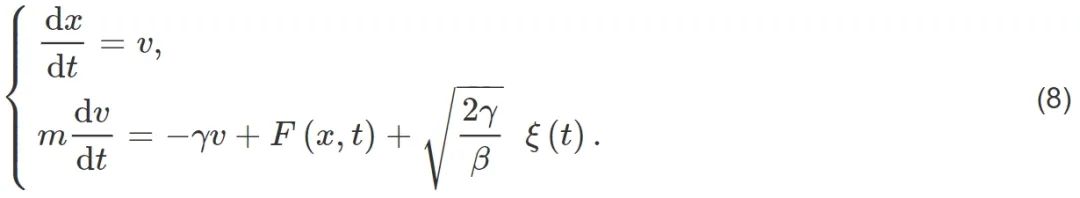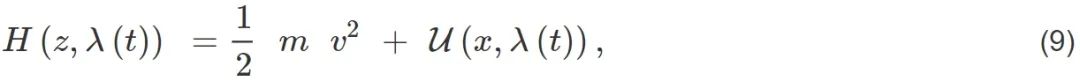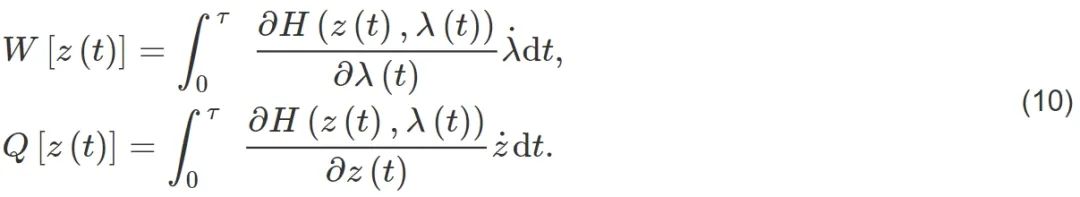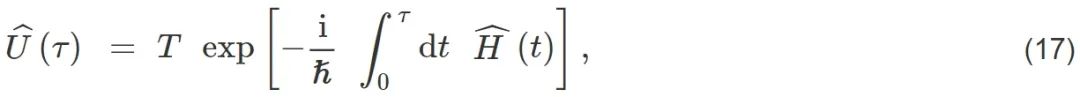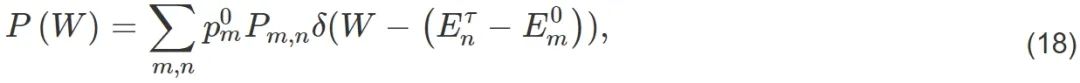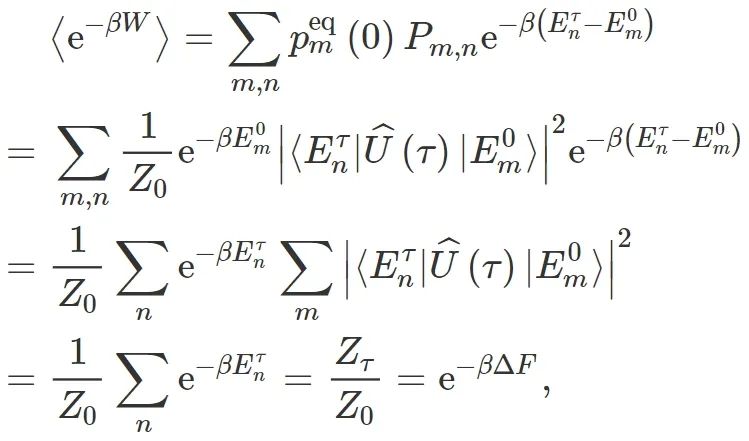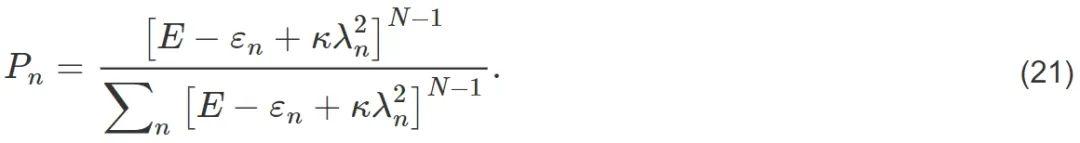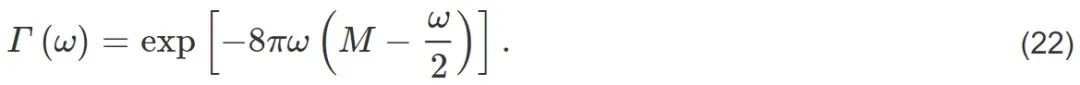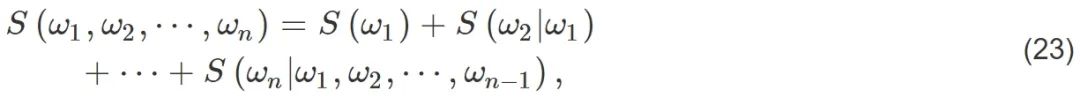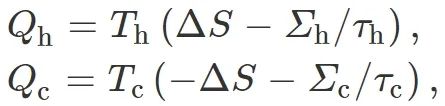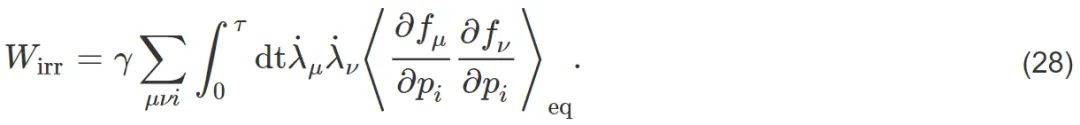对于只有有限自由度的介观小系统,传统的热力学定律是否成立?温度、熵、做功、传热、等温过程、Carnot 循环这些概念还是否有效?是否需要对原来适用于宏观系统的传统热力学理论进行修改或扩充、以适用于这样的小系统?在过去近20年里,我们深入研究了在介观小系统和量子系统中热力学基本概念的推广(例如什么是量子等温过程)以及基本热力学定律的适用性问题。研究表明,在系综平均意义上热力学定律仍然适用于小系统;考虑了Maxwell妖的信息擦除功耗后,热力学第二定律不会被违反;“小系统”的统计热力学具有一些新的特性,由于系统和环境之间的耦合不可忽略,有限系统的平衡态分布偏离正则系综,这可以描述诸如黑洞等小系统的辐射关联及其信息丢失现象;在任意远离平衡的情况下,热力学量的涨落变得十分显著,并且热力学量的分布函数满足一些严格成立的恒等式。这些恒等式定义了所谓的涨落定理,由此通过测量非平衡过程的物理量(如功分布)可以获得平衡过程的物理量相对值(如自由能差等)。此外,尽管量子属性和信息论的考虑为统计热力学带来一些有别于经典和传统的特性,有助于理解 Gibbs 佯谬和 Maxwell 妖等基本问题,但需要指出的是,量子热机和信息辅助热机的效率并没有超越经典热机。随着在小系统中引入运动方程,热力学和力学之间的联系变得更加紧密,能够从第一性原理出发研究非平衡过程的能量耗散和热机的功率、效率优化及其最优调控微分几何化等问题。在对具体热循环过程熵产生问题的研究中,对得到的功率-效率约束关系进行了系统性的实验检验。
为了深入探索统计物理前沿进展,集智俱乐部联合西湖大学理学院及交叉科学中心讲席教授汤雷翰、纽约州立大学石溪分校化学和物理学系教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学物理系助理教授唐乾元,以及多位国内外知名学者共同发起「非平衡统计物理」读书会。读书会旨在探讨统计物理学的最新理论突破,统计物理在复杂系统和生命科学中的应用,以及与机器学习等前沿领域的交叉研究。读书会从12月12日开始,每周四晚20:00-22:00进行,持续时间预计12周。我们诚挚邀请各位朋友参与讨论交流,一起探索爱因斯坦眼中的普适理论!
关键词:随机热力学,有限时间热力学,量子热力学,非正则热化
全海涛(北京大学物理学院),董辉(中国工程物理研究院研究生院),孙昌璞(北京大学物理学院、中国工程物理研究院研究生院) | 作者
物理学报 | 来源
众所周知,传统热力学和统计物理是关于宏观系统 (通常包含1023个以上粒子) 的理论。然而,当系统有限、偏离热力学极限时,传统的热力学和统计物理理论是否依然成立?量子效应是否影响系统的热力学性质?或者统计物理和热力学理论需要做哪些修改或补充?学界对这些基本问题并没有进行充分的研究,对许多困惑也没有形成共识。
在过去的近20年里,随着介观物理、纳米技术和量子信息领域的不断发展,统计热力学的研究经常面临只包含少数粒子,甚至只有几个粒子的体系的挑战。在这种远远偏离热力学极限的系统,原本适用于宏观系统的热力学和统计物理理论是否依然成立,这已经成为亟待解决的基础科学问题,并且在许多实际应用中具有迫切的需求 (如核电池的循环和人工光合作用等领域)。当考虑到极低温情况时,量子效应也不能被忽略。因此,对于介观的小系统,比如Szilard单分子热机,人们必须重新审视热力学和统计物理理论。特别对于不能忽略量子效应的小系统,统计热力学研究已经成为近20年来的研究热点之一。在过去的近20年里,我们在介观小系统的统计热力学及其应用方面开展了一系列的研究,这些研究在国际学术界引起了较大的反响,实质性地推动了这一新兴领域的发展。本文将对该领域的发展,以及我们相关的工作和未来展望方面进行简要介绍。
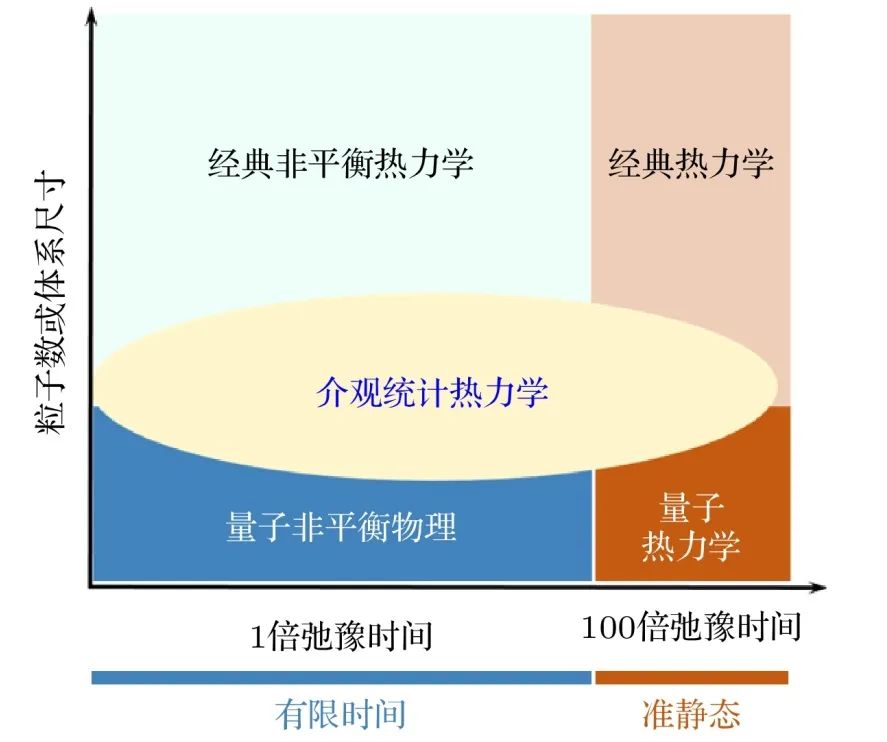
对于小系统,我们用粒子数和过程时间两个尺度刻画其介观特性。一方面,研究对象从宏观到介观和微观,伴随着所研究的物理系统的粒子数或尺寸变小,热涨落和量子涨落变得至关重要,这导致了如小系统非平衡统计物理或者纳米热力学等新兴学科方向的产生,特别是小系统中量子相干性和热库-系统量子纠缠推动了关于统计物理基础理论的前沿研究;另一方面,我们所研究的物理系统的动力学过程时间尺度变短,体系偏离平衡态,这催生出了有限时间热力学等研究方向。其中,动力学控制对热力学过程影响也已成为近些年的热点研究方向。图1总结了统计热力学向介观小系统发展的这一新趋势和前沿方向。
本综述是在笔者及合作者们多年在介观统计热力学领域的研究基础上的总结,同时也反映了国际上热力学发展的趋势:在空间尺度上从宏观尺度走向介观微观量子的尺度;在时间尺度上从平衡态走向有限时间的非平衡过程。需要指出的是,受自身学识的局限和偏好的影响,本文并未试图、也不可能对整个领域进行全面的、或者包罗万象的介绍,只选择了笔者比较熟悉的方面进行阐述。希望能为相关研究者提供一些有价值的参考和借鉴。
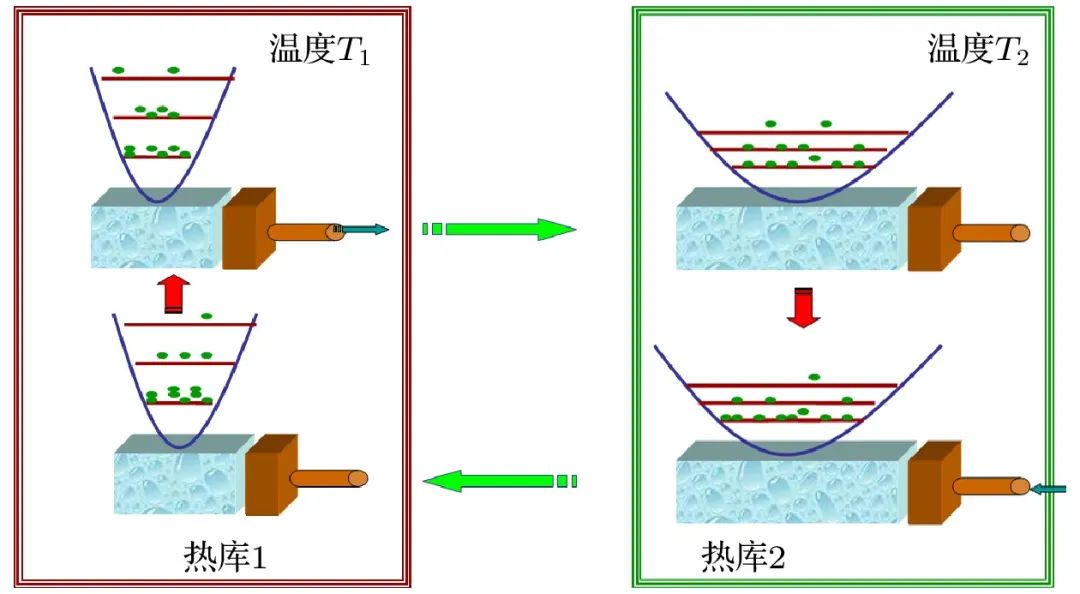
近20年来,受到量子信息发展的带动以及实验技术进步的影响,量子力学和统计物理学的一些基本问题重新受到物理学家的关注。量子热机 (见图2) 为研究这些问题提供了一个很好的平台。顾名思义,量子热机[1-3]是以“量子物质”为工作物质并且把吸热转化为对外做功的机器。由于工作物质的量子属性,量子热机具有很多不同于经典热机的非凡特质。量子热机工作物质的量子性成为一个备受关注的新研究热点[4]。人们试图通过实验发现一些有别于传统热力学理论的新现象和新效应。在理论研究方面,一些超越人们传统观念的新奇结论陆续被发现。比如,在一定条件下,量子热机在每个循环过程中的对外做功量可以超过对应的经典热机[5,6],而且量子热机的效率似乎可以超越经典热机的效率上限——经典Carnot热机的效率[7]。量子热机不仅有助于研究量子力学和热力学的关系,还有助于理解量子测量和量子退相干问题。此外,它还能很好地体现量子和经典热力学系统的差异,帮助我们理解热力学过程中的量子-经典过渡的问题[8]。
然而,在2007年之前,关于单量子系统的热力学研究比较缺乏,有关量子热力学过程和量子热力学循环的概念较为混乱。考虑到这一状况,2007年,笔者及合作者[9]系统地研究了量子系统的热力学过程和热力学循环,澄清了包括量子等温过程,量子等容过程,量子Carnot循环,以及量子Otto循环等量子热力学的基本概念。这方面的相关工作在量子热力学领域产生了较大的国际影响。下文将简述笔者团队在这一领域的研究成果,其中主要包括将做功、传热、等温过程、Carnot热机、Otto热机等概念推广到小量子系统。
平衡态统计热力学建立于经典力学基础之上。然而,微观粒子遵循更基本的量子力学规律,而经典力学只是量子力学的经典近似。因此,如何将统计热力学理论推广到量子系统,尤其是只有少数自由度的小量子系统,是一个值得研究的问题。比如,如何把“做功”和“传热”等经典热力学概念推广到单量子系统,如何在单量子系统中表述热力学第一定律,另外还有一些与此关联的问题,如何描述有限时间内的热力学过程 (即非准静态或非平衡态过程),以及如何刻画小尺度 (非热力学极限) 系统的热力学性质。这些都是长期以来一直被忽视,但又十分重要的问题。由此已经催生出一个专门的领域,被称为量子热力学[10]。下面我们就以具有离散能级的单量子系统为例,将经典热力学的一些概念做量子推广,并介绍一些量子热力学的基本概念,以及我们在本领域的一些工作。首先介绍如何在单量子系统表述“做功”和“传热”。
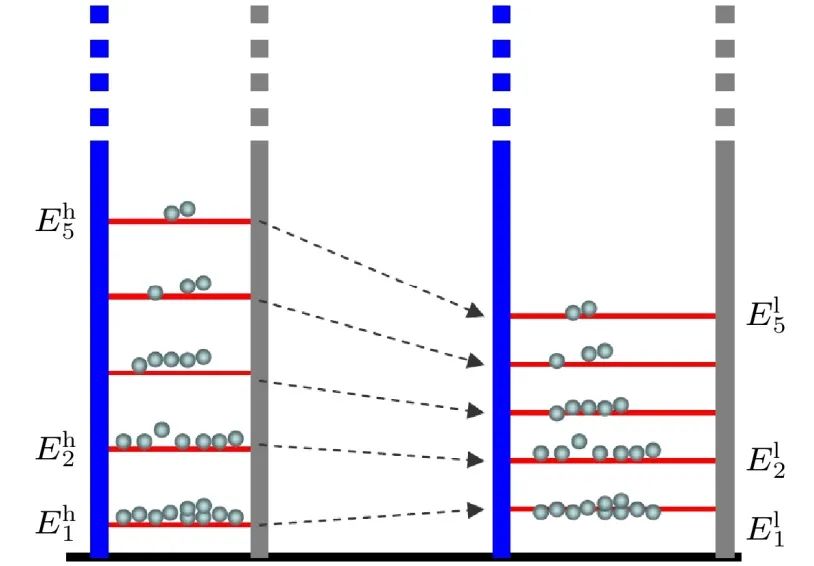
考虑一个任意多能级单量子系统 (见图3)。为了简单起见,考虑的系统只包含离散能级结构,并且只含有有限个本征能级。当然,也可以更一般地考虑具有无穷多个能级的系统。
图3 作为量子热机工作物质的多能级量子系统,这里展示一个量子绝热过程
式中|n⟩是系统的第n个本征态,En是其第n个本征能量。对于这个系统,如果已知其在各个能级上的布居数Pn,那么其内能U可以表示为
为了将一些基本的热力学过程推广到单量子系统,也就是定义单量子系统的等温过程和等容过程,需要先找到传热δQ和做功δW在单量子系统的表述。从方程(2)可以得到:
其中δQ =TdS,δW =∑iYi dyi [11];T 和S分别是温度和熵;yi 是广义坐标,Yi 是与yi 共轭的广义力。考虑到von Neumann熵S和各个本征能级En上的布居数Pn的关系 (kB是Boltzmann常数) :
可以定义单量子系统的热传递和做功[12-14]如下:
方程(6) 意味着“做功”相应于本征能级En的改变。这一点与另一个常识性的结论一致,即做功必然伴随着系统的广义坐标的改变。而在单量子系统中,广义坐标的改变又导致了系统本征能量的改变。因此,通过方程(6)和(7)关于做功和热传递在单量子系统的表述,热力学第一定律在单量子系统的表述dU =δQ +δW就可以从方程(4)得到。需要强调的是,基于方程(6)和方程(7)关于做功和传热的定义,可以建立一套自洽的统计热力学理论。在这个理论体系里面,压强p和体积V不再是基本的,也不再是必需的参数。而{En}和{Pn}才是建立统计热力学理论所必需的元素。可以在某些无法定义压强和体积的系统,比如一个谐振子或者一个二能级系统利用方程(6)和方程(7)建立自洽的统计热力学理论。当然,对于可以明确定义压强和体积的系统,比如活塞中的气体,方程(6)和方程(7)给出的做功和传热的定义与δQ =TdS, δW =−pdV一致。由此可见方程(6)和方程(7)是更一般的、比δQ =TdS, δW =−pdV适用范围更广的关于做功和传热的定义。此外,还需要强调,经典系统的热传递表达式δQ =TdS, δW = ∑iYi dyi 仅仅适用于准静态过程。与之一致的是,量子系统的做功和传热的方程(6)和方程(7)也只适用于准静态过程。在2007年之前的文献[7,15]中,关于量子热机 (比如量子Carnot热机和量子Otto热机) 的定义并不一致,有的甚至互相矛盾。因此量子Carnot热机和量子Otto热机的性质难以清晰阐明。这种情况促使我们为各种量子热机循环提出普适的定义。任何一个量子热机的循环都是由若干基本的量子热力学过程组成的。有了单量子系统做功和传热的定义,就可以研究单量子系统的热机循环。下文将描述 (由这些量子热力学过程构成的) 平衡态热力学循环的性质,同时将量子热机的性质与经典热机的性质进行比较。
经典Carnot热机是一种非常典型的热机,其每个循环的4个冲程的热力学性质都非常清晰,而且它代表了一类普适的可逆热机的物理机制。目前,关于量子热机的研究大多集中在对经典Carnot热机的量子力学推广方面,也就是对量子Carnot热机有关方面的研究。
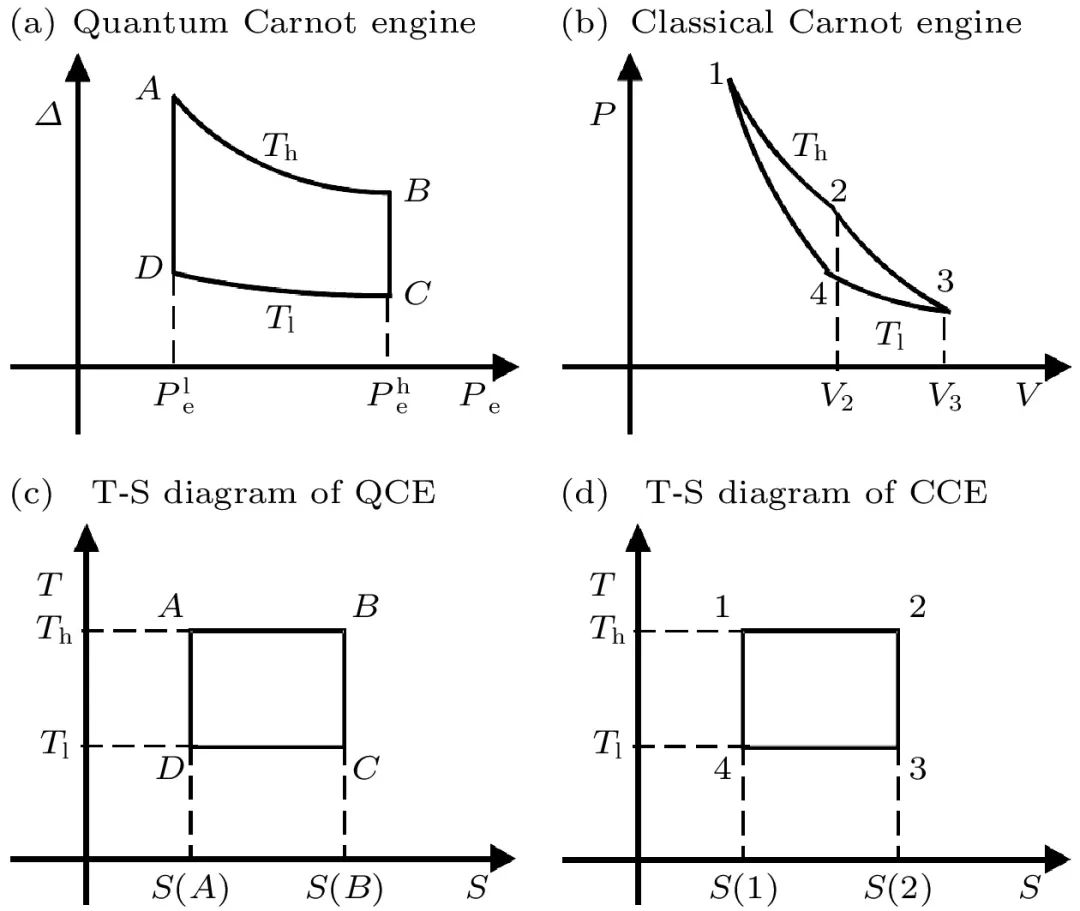
量子Carnot热机 (一个基于二能级系统的量子Carnot热机循环的示意图见图4),如同与其对应的经典Carnot热机一样,由两个(量子)等温过程A→B及 C→D和两个 (量子) 绝热过程B→C及D→A构成。在等温膨胀过程A→B中,工作物质,即被束缚在势阱中的一个粒子始终与一个温度为Th的热源相接触。工作物质的能级改变的速度比系统的弛豫速度慢得多,以至于这个粒子一直与热库保持在热平衡状态。
图4 一个基于二能级量子系统的量子Carnot热机循环,Th和Tl分别代表高温和低温热库的温度,Δ和Pe代表二能级系统的能级差和激发态上的布居数,P和V代表经典理想气体的压强和体积
要使量子热机对外做正功,热机的两个热库必须满足条件Th>Tl。这个对量子Carnot热机的限制也就是所谓的量子Carnot热机的“正功条件”,和经典Carnot热机的“正功条件”是一样的。此外,为了说明定义的量子Carnot热机是经典Carnot热机的量子力学对应,在图4(c),(d)中给出了量子和经典Carnot热机循环的温度-熵循环 (T–S) 图。从图中可以看到,经典和量子的Carnot循环的T–S图具有完全相同的形式。基于上述理由,可推断本文给出的量子 Carnot 热机循环是经典 Carnot 热机循环的量子力学对应。
量子Otto热机循环是另一类很重要的量子热机循环,其也引起了很多关注。与Carnot循环类似,经典Otto循环的量子力学对应也有很多研究[9]。实际上,汽车的内燃机所进行的循环就是经典Otto循环 (而非经典Carnot循环)。Otto循环由两个经典的等容过程和两个经典的绝热过程构成。量子Otto循环由两个量子等容过程和两个量子绝热过程组成。需要指出的是,文献[1]中提到的第1个量子热机模型事实上是一个量子Otto热机模型。因为它的热机效率和正功条件分别是1−Δ1/Δ0和Th>(Δ0/Δ1)Tl,其中Δ1及Δ0分别是工作物质的两个能级差,Th和Tl分别是两个热库的温度。
从研究结果可以看出,尽管量子属性会带来一些有别于经典的特征,但是基于单量子系统的量子热机的性能并没有超越经典热机。而在量子信息领域,量子信息处理相比于经典信息处理具有显著的优势,两者形成了鲜明的对比。
1860年左右,Clausius和Kelvin独立提出了热力学第二定律。之后不少物理学家曾一度对其普适性持有怀疑态度。一些研究者提出各种“反例”,试图说明热力学第二定律可能违反概率性。其中一个重要的例子是物理学家Maxwell在1871年提出来的一个思想实验。后来这个思想实验中的假想智慧生命被开尔文命名为Maxwell妖,并且引起了很多物理学家的兴趣。多位物理学家前赴后继投入大量精力去研究这个思想实验,以及其与热力学第二定律可能矛盾的方面[16]。对Maxwell妖的研究持续了一百多年。直到1982年,这个困扰物理学界一个多世纪的难题才最终被物理学家Bennett利用Landauer原理 (Landauer在研究计算能耗时提出的) 解决。下文将简述这段热力学发展史上著名的思想实验,并介绍我们在这个领域的一些工作。
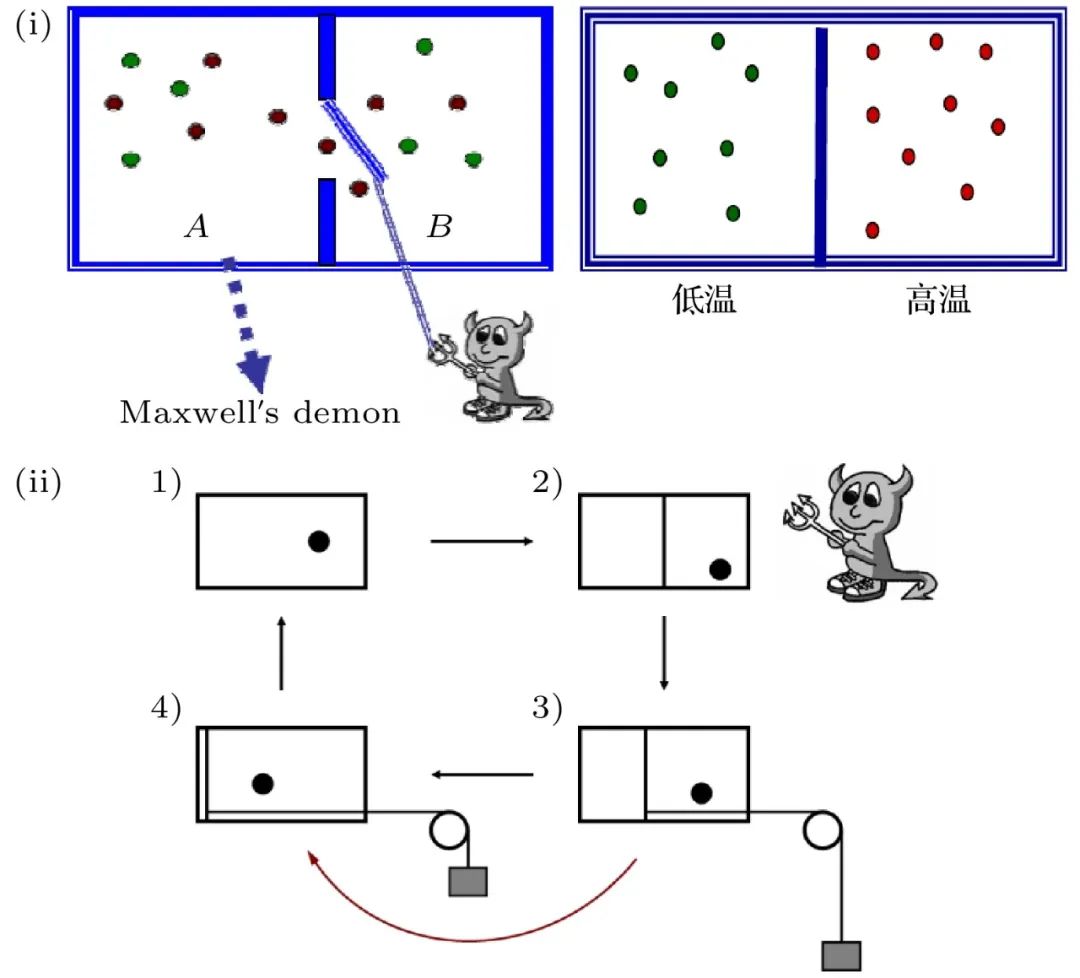
Maxwell妖是一种能够区分单个气体分子速度的假想物 (见图5(i)),它能够让一个容器内运动快 (“热”) 的分子和运动慢 (“冷”) 的分子分别占据不同的区域,从而使容器中不同区域的温度不同[16]。这个结论似乎与热力学第二定律相违背:当把高温和低温分子集合当成两个热源,在它们之间放置的热机,能够利用温差对外做功。整体来看,Maxwell妖的引进,使得“从单一热源吸热完全转化为对外做功”成为可能,从而出现了违反热力学第二定律的第二类永动机。这就是“Maxwell妖佯谬”。在相当长的时间内,物理学家们没有能够对“Maxwell妖佯谬”给出一个很满意的解释。这个问题的一个重要的进展是1929年物理学家Szilard[17]引入的单分子热机模型 (见图5(ii))。在这个简化了的Maxwell妖热机模型中,Szilard首次将信息的概念引入到热力学循环中。他直观地认为,Maxwell妖测量分子处于左边还是右边是一个获取信息的过程,可能会消耗能量,从而导致整体的熵增大。如果把这个消耗包含到热力学循环中来,就不违反热力学第二定律,Maxwell妖佯谬也就迎刃而解。
图5 Maxwell妖和Szilard单分子热机模型
可是Szilard[17]的解释并没有被最终接受,在随后的几十年内,对这个问题的争论一直没有停止。直到1961年,有关Maxwell妖佯谬的研究有了一个革命性的突破。在研究计算过程的热力学本质时,物理学家 Landauer[18]发现了一个著名定理:每擦除1 bit的信息将会导致kBTln2—10−21 J热量的耗散。这就是本文所述的Landauer原理,其将信息理论和物理学的基本问题联系在一起。这个原理提出后不久,Landauer的同事Bennett[19]意识到信息擦除与Maxwell妖佯谬问题有极其密切的关系,并在1982年利用Landauer原理从原理上解决了Maxwell妖佯谬[16]。Landauer原理的实验验证由Bérut 等[20]于2012年完成。过去15年左右,产生了一个与Maxwell妖相关的前沿研究领域——信息热力学[21],其是Maxwell妖相关研究与随机热力学相结合的产物。
2006年,笔者和合作者研究了如何利用超导量子比特实现包含Maxwell妖的热力学循环[22,9,23],研究动机是如果在量子领域存在Maxwell妖,是否会从本质上改善量子热机的效率?研究中量子测量被处理成一个产生系统和测量仪器之间的理想量子纠缠的相互作用动力学过程,避免了使用在基本观念上备受争议的波包塌缩假设。因此,从根本上改进了原来的包含Maxwell妖的量子热机模型,让一个充当热机介质的二能级系统S首先与温度为TS的热库接触,而另一个充当Maxwell妖的二能级系统D被置于温度为TD的热库当中。开始时二者均处于热平衡态,然后脱离热库。用D测量S所处的态,并根据测量结果对S进行反馈控制 (采用可控的CNOT门),如果S处在激发态上,D就将其翻转到基态上;如果S处在基态上,D就让其保持不变。最后让它们分别与各自的热库充分接触,在达到热平衡态后,完成一个热力学循环。计算表明,这样热机的效率形式上为η=1−ςΔD/ΔS,其中ΔD和ΔS是两个二能级系统的能级差。ς是一个与D和S初始分布有关的物理量。通过分析发现在特定的条件下,比如TD足够低时,这个热机等价于一般的量子Otto热机。详情见文献[22]。总体而言,包含Maxwell妖的热机没有违背热力学第二定律的现象。另外,我们还提出了基于超导量子电路的Maxwell妖量子热机的物理实现及其量子操控方案。
作为Maxwell佯谬的一个重要模型,Szilard单粒子热机引入信息控制的概念,突显了信息在有限系统热力学中的作用。当时热力学中的一个重要问题是如何体现Maxwell妖在参与量子热机的热力学循环中的具体作用。我们构造了一个全量子的Szilard单粒子热力学循环[24]:热机主要是由束缚在一维无限深势阱中的单粒子以及一个可以移动的壁构成,Maxwell 妖则是由一个二能级系统构成。让Maxwell 妖处在与热机不同的温度上,实际上我们构造了一个在不同温度之间工作的热机。在这种有Maxwell 妖辅助的系统中,量子相干性确实有助于提高热力学循环的工作效率。通过证明热机的工作效率低于理想的Carnot热机,说明Maxwell 妖的存在实际上并不会破坏热力学第二定律。基于类似的循环,在全同多粒子体系的Szilard循环中也得出了同样的结论[25],并发现全同统计性质对循环效率的影响。
1982年Bennett[19]的开创性工作虽然说明Maxwell妖不会对热力学第二定律构成威胁,即擦除其存储单元的信息,保证热力学第二定律不会被违反,但是他的假想实验似乎仍然没有完全摆脱“智慧精灵”这个假设。有“智慧精灵”参与的 (非自动化的) 信息热机模型不可能在实验室实现,因为世界上不存在这样的“智慧精灵”。那么,是否有可能设计一个完全自动化的Maxwell热机或Maxwell制冷机?即没有任何“智慧精灵”的参与,这个机器能够实现Maxwell最初的设想,并且得到和Landauer原理预言相一致的结果。如果能够构造出一个自动化的信息热机模型,将有希望在实验室中真正制造出一个信息热机或信息擦除器,从而实现Maxwell最初的设想。这个装置不仅可以帮助理解信息、熵、热、功这些物理学基本概念,还具有很重要的应用前景。2013年Mandal等[26]考虑了一个自动化的信息制冷机模型。与信息热机类似,这个自动化的模型通过消费输入的存储单元利用热涨落将热量从低温热库输送到高温热库,或者相反通过消费高温热库的热量,实现对存储单元上信息的 (部分) 擦除。这个模型真正体现了Maxwell在1871年提出的思想实验的内涵。有关这个模型的更详细的情况请参阅文献[26]。
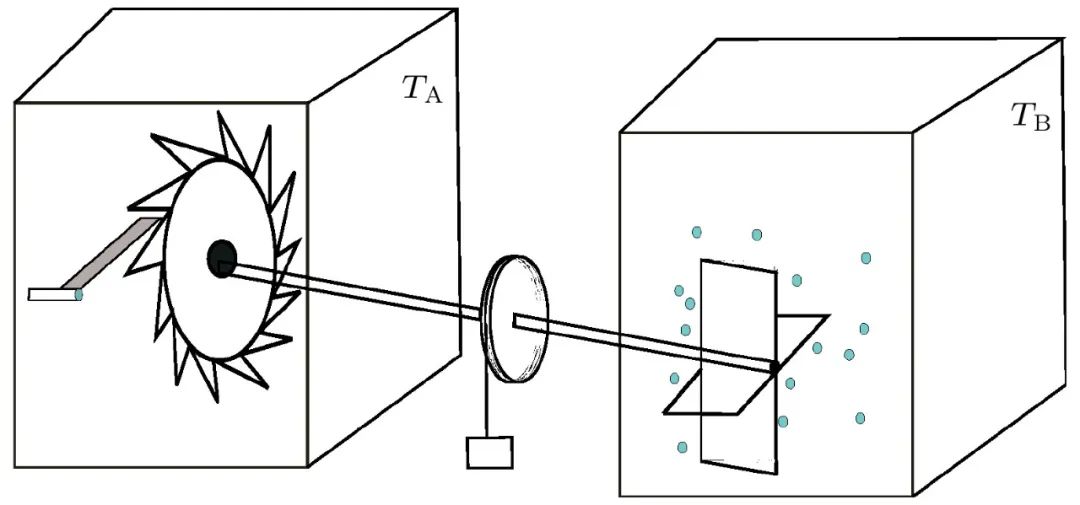
当系统偏离热力学极限时,小系统的热力学量的平均值不足以描述系统的全部行为,此时涨落变得至关重要。事实上,热力学量的涨落蕴含了丰富的非平衡过程的信息,对热力学量涨落的研究深化了对热力学第二定律的理解。1961年Feynman提出一个思想实验,即Feynman棘轮的装置 (见图6)。如果只考虑热力学量的平均行为,而不考虑涨落,就无法理解Feynman棘轮的工作原理。考察这一系统的能量转化时,传统功和热的定义已然失效。1997年,Sekimoto[27]在研究Feynman棘轮系统时首次将功和热定义在了单条随机轨道之上 (几乎在同时,Jarzynski[28]独立引入了轨道功的概念,与Sekimoto引入的轨道功定义一致),直接催生了随机热力学这个领域。
图6 Feynman棘轮,TA和TB代表两个热库的温度,有关Feynman棘轮的介绍可参考文献[27]
随机热力学在随机轨道意义上定义热力学量并重新表述热力学第一定律和第二定律。下面我们用一个具体的例子阐释随机热力学的主要定义和内容。考虑这样一个过程,系统与温度为T 的热库接触,系统受一个随时间改变的外部参量λ(t)控制,比如活塞系统的长度、谐振子系统的频率等等。λ(t)改变的同时便是外部对系统做功,所以λ(t)也被称为功参量[29]。初始时刻t=0时系统处于一个态,t=τ为终止时刻,系统处于另一状态,只要λ(t)改变得不是无穷缓慢 (即准静态过程),那么过程中每一时刻 (包括末态) 都是非平衡态,整个过程便是非平衡过程。以一维胶体粒子系统为例,粒子满足朗之万方程:
(8)式是描述布朗粒子在相空间(x,v)的随机轨道随时间t的演化方程,其中x为位置,v为速度。(8)式中m为粒子的质量,γ为Stokes黏滞系数,β =kBT −1为温度倒数,F(x,t)代表势场力F(x,t) =−∂U(x,λ(t))/∂x,其中U(x,λ(t))代表势场。(8)式中速度方程的最后一项代表随机力,其中ξ(t)是归一化的白噪声,满足⟨ξ(t)⟩= 0,⟨ξ(t)ξ(t′)⟩=δ(t−t′),其中尖括号代表平均的含义。
不同于传统热力学,微观系统中的做功和传热需要重新定义,它们都是随机轨道 [z(t)] 的泛函。1997 年,轨道功W和轨道热Q的定义由物理学家 Jarzynski[28,30]和Sekimoto[27,31]分别独立给出 (这里指外界对系统所做的功W和系统从外界吸的热Q) :
由朗之万方程(8)可知,轨道热是阻尼力和随机力的贡献,正好可以表示成系统哈密顿量因为相空间坐标的改变而产生变化;那么剩余部分,即系统哈密顿量因为功参量λ(t)的改变而产生变化,便被定义为功。这样的定义保证了热力学第一定律,即能量守恒:
有了功、热和熵产生的定义,热力学第二定律也可以被重新表述。在小系统中,由于有涨落的存在,热力学第二定律将只会在统计平均的意义上成立[29,32]:
其中ΔF为过程前后系统的自由能差。(11)式和(12)式的具体证明会在下一节涨落定理中给出。
除了以上轨道功、热、熵产生的定义之外,随机热力学中引入的其他热力学量还包括更加细致的 housekeeping 热、excess 热[33,34]、环流[32,35,36]等概念。这些是近些年Esposito等[37-39]工作的基础。
对于小系统的非平衡过程,物理学家从1993年开始陆续发现了很多对于任意原理平衡过程都严格成立的恒等式,统称为涨落定理。而热力学第二定律作为推论从涨落定理导出。涨落定理有很多,其中最著名的结果便是 Jarzynski 恒等式,由 Jarzynski [28,30]于 1997 年提出:
Jarzynski 恒等式成立的条件是初态为热平衡态。对 Jarzynski 恒等式利用一次Jensen不等式⟨ex⟩⩾e⟨x⟩,便很容易得到(12)式,即热力学第二定律。另外可以看到在小系统热力学第二定律会有一定的概率被“违反”。其概率由公式P[W<ΔF−ζ]⩽e−βζ给出[40]。当系统的自由度足够少,ΔF和W只有kBT量级时,这种“违反”具有明显的可观测效应。但是随着系统自由度增加,这种“违反”热力学第二定律的概率呈指数级降低,在宏观系统变得不可能。Jarzynski 恒等式最大的意义在于将一般非平衡过程中热力学量满足的不等式关系改写成了恒等式,这是非平衡热力学领域具有里程碑意义的创新。另外,Jarzynski 恒等式指出,平衡态自由能差值可以通过任意非平衡过程来进行测量,即平衡态的信息可以从非平衡过程得到[29],这在分子的自由能实验测量领域,尤其是纳米尺度的实验中得到了广泛的应用[41,42]。值得指出的是,Jarzynski 因为他的这项开创性的研究,被美国物理学会授予2019年度 Las Onsager 奖。而用来验证 Jarzynski 恒等式的工具——光镊技术的发明人 A. Ashkin 被授予2018年度诺贝尔物理学奖。
理论上,Jarzynski 恒等式可以经由多种途径推导出来[30]。另外,它的正确性和普适性 (任意系统、任意温度、任意速度) 通过了很多数值模拟研究的检验和实验验证[30]。作为最早被发现和至今仅有的几个描述任意远离平衡过程的热力学恒等式 (另外还有Crooks涨落定理[43]等) 之一,它为研究远离平衡过程的热力学打开了一扇窗。
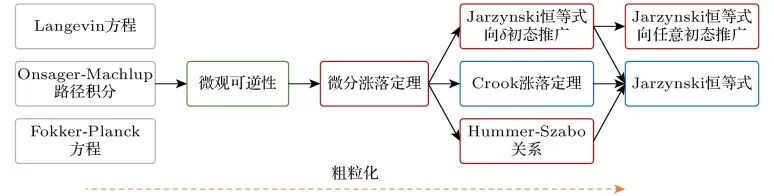
Jarzynski 恒等式的发现是热力学研究历史上的一座里程碑。它首次建立了远离平衡过程的恒等式。在那之后研究人员陆续发现了一些比Jarzynski恒等式更加细致的涨落定理,比如Crooks涨落定理[43]、Hummer-Szabo涨落定理[44]和微分涨落定理[45,46]。这些涨落定理构成了一个“家族”。文献[47]整理了这些涨落定理之间的逻辑关系,参见图7。
图7 涨落定理家族,这些涨落定理并不互相等价,箭头代表“可以推导出”,详情见文献[47]
不难看出“微分涨落定理”在整个领域占据着特别重要的地位。其他涨落定理都可以从这个最基本的涨落定理推导出来。虽然Jarzynski恒等式等粗粒化的涨落定理早在2002—2005年前后就已经在多种实验系统中 (比如单个RNA 分子链和水溶液中的胶体粒子) 得以验证,但是“微分涨落定理”的实验验证却一直是一项巨大的挑战,因为测量胶体粒子的瞬时速度对实验技术提出了极高的要求。2017 年,本文作者之一和美国普渡大学的李统藏教授研究组[47]合作,借助他们发展出来的超高时空分辨的光力系统实验平台,测量了束缚在空气中的纳米小球在激光驱动时位置和瞬时速度随时间的演化。通过获取大量轨道数据,第一次在实验上验证了这个被称为涨落定理之母的“微分涨落定理”。这项工作将随机热力学实验研究从过阻尼情形拓展到了欠阻尼情形,并且把这个最基本的涨落定理乃至所有其他的有关非平衡功的涨落定理都建立在了坚实的实验基础之上。
值得指出的是,在这些涨落定理中,越粗粒化的发现得越早,越精粒化的发现得越晚。考虑到涨落定理是对热力学第二定律的不同形式的推广,不难得到如下结论:物理学家对热力学第二定律的认识也是循序渐进,逐步深入的。这一点与物理学家对原子结构的认识过程非常相似。
除了与功有关的涨落定理,还有一个有关热交换的涨落定理[48],它描述的是一个初始时处于温度βs的系统跟一个处于温度β的热库在接触过程中热交换满足如下的恒等式[48]:
其中Q是系统从热库吸热。利用Jensen不等式,可以得到
(15)式为Clausius不等式,只能从相对的高温热源吸收热量。如果把有关做功和热交换的涨落定理合并起来考虑,可以得到一个多热库时的,关于功和热的联合分布的涨落定理[49]:
式中βν是第ν个热库的温度;ΔF是系统的自由能之差。这个多热库的涨落定理可以分别回到Jarzynski恒等式,或者有关热交换的涨落定理。因此,可认为这个不等式是有关做功和热交换的涨落定理的最一般的形式,它将所有关于非平衡做功和传热的涨落定理统一在一个公式里。有关详细内容见文献[49]。
以上关于功和热的涨落定理都是在细致平衡条件成立时的结果。当细致平衡条件不成立时,还有其他一些涨落定理:比较知名的有Evans-Searles涨落定理[50,51]和Gallavotti-Cohen涨落定理[52,53]。从这些细致平衡条件被破坏的涨落定理出发,还可以推导出所谓的热力学不确定性关系[54,55]。由于篇幅所限,对这些内容不再详述。
研究人员最初对有关随机热力学和涨落定理的研究主要聚焦于经典系统,此后开始思考将热力学的理论框架和涨落定理推广到量子系统。向量子力学的推广并不是非常直接的,因为量子系统的微观状态用Hilbert空间的矢量表示,而经典系统的微观状态用相空间的一个点代表。另外,量子系统里的测量、波函数塌缩、量子轨道等概念与经典系统具有明显的区别。经典粒子在相空间有很好定义的轨道,从而可以定义轨道功、轨道热等概念,但由于量子不确定性原理,对量子系统不能很好地定义轨道。这些区别给量子随机热力学和量子涨落定理的研究带来了挑战。下面简要介绍把随机热力学和涨落定理向量子系统的推广。
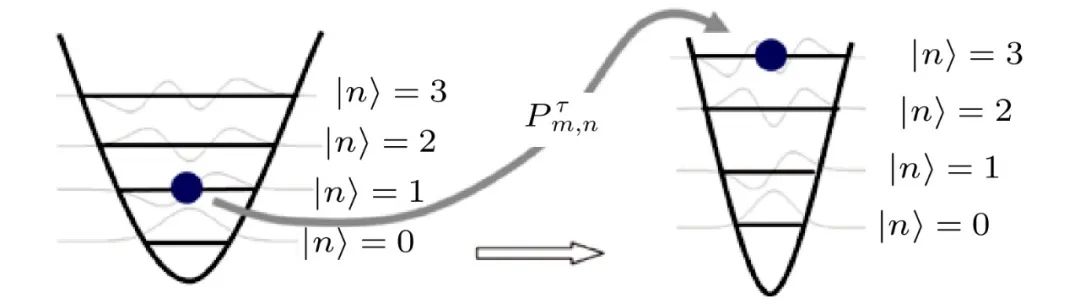
量子孤立系统是指在驱动过程中,系统不与外界热库发生相互作用,所以没有热交换。在量子孤立系统中,系统的幺正演化算符为
其中T是编时算符。在整个驱动过程中,外界对系统会做功W。由于是量子孤立系统,过程中并没有与热库的热交换,那么做功值便是演化前后的能量差。标准的量子功的定义是基于两次能量投影测量 (two-projective energy measurement,TPM) W :=Enτ−Em0,2000年由Kurchan[56]和 Tasaki[57]分别独立提出。即在初始时刻时先做一次能量投影测量,譬如系统的态塌缩到了初态哈密顿量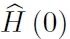 的第m个能量本征态,然后从这个能量本征态开始演化,在终止时刻时再进行一次能量投影测量,这时系统的态可能塌缩到了末态哈密顿量
的第m个能量本征态,然后从这个能量本征态开始演化,在终止时刻时再进行一次能量投影测量,这时系统的态可能塌缩到了末态哈密顿量 的第n个能量本征态,整个过程称为一次实验。在这次实验中,能量差W便被定义为量子功。当然可以重复很多次实验,每次得到的功的值都可能不一样,最后便有一个功分布P(W)。整个过程的示意图见图8。
图8 基于两次投影定义的轨道功。这里显示了一次实验的结果,从第2个本征态跳到第4个瞬时本征态
功分布不仅与初态的概率分布pm0有关,还与跃迁矩阵元Pm,n有关:
式中pm0为第一次测量得到第m个本征态的概率,即为
的第n个能量本征态,整个过程称为一次实验。在这次实验中,能量差W便被定义为量子功。当然可以重复很多次实验,每次得到的功的值都可能不一样,最后便有一个功分布P(W)。整个过程的示意图见图8。
图8 基于两次投影定义的轨道功。这里显示了一次实验的结果,从第2个本征态跳到第4个瞬时本征态
功分布不仅与初态的概率分布pm0有关,还与跃迁矩阵元Pm,n有关:
式中pm0为第一次测量得到第m个本征态的概率,即为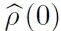 的第m个对角元。Pm,n为跃迁矩阵元,表示从初始时刻的第m个本征态跃迁到终止时刻的第n个本征态的概率:
基于 TPM 的量子功的定义最大的好处是满足量子 Jarzynski恒等式[56-58],形式与经典情形下的 Jarzynski 恒等式(13)式完全一致,成立条件仍需要初态为热平衡态:
的第m个对角元。Pm,n为跃迁矩阵元,表示从初始时刻的第m个本征态跃迁到终止时刻的第n个本征态的概率:
基于 TPM 的量子功的定义最大的好处是满足量子 Jarzynski恒等式[56-58],形式与经典情形下的 Jarzynski 恒等式(13)式完全一致,成立条件仍需要初态为热平衡态: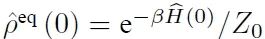 ,其中Z0为初始时刻的配分函数
,其中Z0为初始时刻的配分函数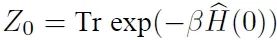 。量子Jarzynski恒等式的简单证明如下[56,57]:
其中用到了幺正演化算符
。量子Jarzynski恒等式的简单证明如下[56,57]:
其中用到了幺正演化算符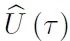 的幺正性质。
2013年两个研究组[59,60]提出间接验证量子Jarzynski恒等式的方案——将功分布的傅里叶变换映射为一个量子开放系统的退相干因子。通过测量这个退相干因子间接获得功分布的信息。这个方案最终在2014年被实验验证[61]。量子Jarzynski恒等式的直接实验验证由本文作者之一与清华大学金奇奂教授[62]合作完成。通过发展一种适用于单离子的声子投影测量技术,最终实现了对量子力学系统做功的测量,并成功验证了量子Jarzynski恒等式。这个工作在非平衡统计物理领域产生了一定的国际影响。
在经典力学和经典热力学中,功的定义非常清楚,但相应的量子力学的做功一直困扰着物理学家。2000年,Jarzynski刚提出他的恒等式不久,法国物理学家Kurchan[56]和日本物理学家Tasaki[57]就很快将Jarzynski恒等式推广到了量子力学系统。不过,他们为了得到这个量子Jarzynski恒等式,引入了一个非常反直观的基于两次投影定义的量子轨道功的概念,而量子投影意味着波包塌缩假设,这在量子力学中是有争议的。从2000-2015年,量子轨道功的定义和内涵一直是研究的焦点,但几乎没有任何进展。
2015年,本文作者之一和合作者[63]对这个非平衡统计物理的重要问题——量子力学轨道功的定义和内涵进行了深入研究,利用半经典力学的办法,第一次严格解析证明了量子轨道功满足量子力学“对应原理”,并第一次揭示了量子力学的轨道功和经典力学的轨道功的联系。这为基于两次投影方法定义的量子轨道功找到了一个佐证,从而在一定程度上证明了基于两次投影定义的量子轨道功的合理性。2018年本文作者之一和合作者Ken Funo[64]又进一步把上述工作向前推进。首次将路径积分方法引入到量子开系统的热力学研究中。具体说来,该项研究引入了一种全新的办法 (定义单条费曼路径上的轨道功),从而可以更好地阐明量子轨道功和经典轨道功之间深刻的内在联系,而且可以很方便地把功分布的对应原理从原来的孤立系统推广到量子开放系统。
在平衡态统计物理中,统计配分函数包含了热平衡态的重要信息。因此发展各种解析和数值方法计算一个物理系统的配分函数成为平衡态统计物理研究的重要内容。与之类似,对于一个非平衡驱动过程,它的功分布函数和热分布函数包含了有关非平衡过程的重要信息。发展各种方法计算非平衡过程的功分布和热分布函数称为非平衡统计物理研究的重要内容。笔者团队在这个方面也进行了一些探索。我们计算了活塞中单个布朗粒子在等温过程的功分布[65],腔量子电动力学系统[66]及有相互作用的量子多体系统[67]在绝热过程的功分布。此外,还用路径积分方法研究了量子开系统的轨道热满足的涨落定理[68,69],以及具有对偶关系的一维玻色系统与一维费米系统的做功的全同性[70],这种对偶性也会体现在以这些量子多体作为工作物质的量子热机的效率[71]。这些研究显著拓展了对量子系统做功的理解。
的幺正性质。
2013年两个研究组[59,60]提出间接验证量子Jarzynski恒等式的方案——将功分布的傅里叶变换映射为一个量子开放系统的退相干因子。通过测量这个退相干因子间接获得功分布的信息。这个方案最终在2014年被实验验证[61]。量子Jarzynski恒等式的直接实验验证由本文作者之一与清华大学金奇奂教授[62]合作完成。通过发展一种适用于单离子的声子投影测量技术,最终实现了对量子力学系统做功的测量,并成功验证了量子Jarzynski恒等式。这个工作在非平衡统计物理领域产生了一定的国际影响。
在经典力学和经典热力学中,功的定义非常清楚,但相应的量子力学的做功一直困扰着物理学家。2000年,Jarzynski刚提出他的恒等式不久,法国物理学家Kurchan[56]和日本物理学家Tasaki[57]就很快将Jarzynski恒等式推广到了量子力学系统。不过,他们为了得到这个量子Jarzynski恒等式,引入了一个非常反直观的基于两次投影定义的量子轨道功的概念,而量子投影意味着波包塌缩假设,这在量子力学中是有争议的。从2000-2015年,量子轨道功的定义和内涵一直是研究的焦点,但几乎没有任何进展。
2015年,本文作者之一和合作者[63]对这个非平衡统计物理的重要问题——量子力学轨道功的定义和内涵进行了深入研究,利用半经典力学的办法,第一次严格解析证明了量子轨道功满足量子力学“对应原理”,并第一次揭示了量子力学的轨道功和经典力学的轨道功的联系。这为基于两次投影方法定义的量子轨道功找到了一个佐证,从而在一定程度上证明了基于两次投影定义的量子轨道功的合理性。2018年本文作者之一和合作者Ken Funo[64]又进一步把上述工作向前推进。首次将路径积分方法引入到量子开系统的热力学研究中。具体说来,该项研究引入了一种全新的办法 (定义单条费曼路径上的轨道功),从而可以更好地阐明量子轨道功和经典轨道功之间深刻的内在联系,而且可以很方便地把功分布的对应原理从原来的孤立系统推广到量子开放系统。
在平衡态统计物理中,统计配分函数包含了热平衡态的重要信息。因此发展各种解析和数值方法计算一个物理系统的配分函数成为平衡态统计物理研究的重要内容。与之类似,对于一个非平衡驱动过程,它的功分布函数和热分布函数包含了有关非平衡过程的重要信息。发展各种方法计算非平衡过程的功分布和热分布函数称为非平衡统计物理研究的重要内容。笔者团队在这个方面也进行了一些探索。我们计算了活塞中单个布朗粒子在等温过程的功分布[65],腔量子电动力学系统[66]及有相互作用的量子多体系统[67]在绝热过程的功分布。此外,还用路径积分方法研究了量子开系统的轨道热满足的涨落定理[68,69],以及具有对偶关系的一维玻色系统与一维费米系统的做功的全同性[70],这种对偶性也会体现在以这些量子多体作为工作物质的量子热机的效率[71]。这些研究显著拓展了对量子系统做功的理解。
近些年来,量子信息的发展使得人们对量子纠缠有了更加深入的理解,从新的角度开展了统计物理理论基础的创新研究。统计物理学的一个基本假设是等概率假设,并由此发展出基于微正则系综、正则系综以及巨正则系综的统计热力学理论。通常的教科书从热库加系统构成的微正则系综假设出发,推导出系统的正则系综 (吉布斯) 分布。近些年这方面的研究表明,可以不基于上述等概率基本假设,而直接利用量子纠缠的观念,建立正则系综 (吉布斯) 分布[72-74]。
我们把系统之外的部分统称为环境,以区别于通常有温度的热库。整个系统 (系统加环境) 的波函数通常是一个纠缠态。在我们的模型中[75],系统是一个个多能级的系统,其基矢量|n⟩对应能级为εn(n = 1,2,···);环境由N个模式频率为{ωj}的谐振子构成(aj是j模式的消灭算子)。二者之间的“最小”相互作用为HI=∑λn|n⟩⟨n|(gjaj+h.c.),系统的本征能量为E(n,{nj})=εn−κλn2+∑njωj。对于环境和系统组成的整体系统,其能量被限制在一个变形能壳上,如图9所示。
图9 能壳变形图,其中红色是无相互作用的能壳,蓝色为有相互作用的修正
系统的状态可以通过整体能壳上纯态|ψ⟩=∑Cn,{nj}|n,{nj}⟩约化掉环境自由度得到,即ρS=TrB[|ψ⟩⟨ψ|]=∑Pn|n⟩⟨m|+∑Fnm|n⟩⟨m|。可以证明Fnm具有因子化结构,并且在环境自由度足够大的时候趋近于零,即Fnm→0。根据概率论中的大数定律,可以证明对角项Pn=∑∣Cn,{nj}∣2的平均值为Pn=Ω(E−εn,δ)/Ω(E,δ),其中Ω(E−εn,δ)是环境在能壳[E−εn,E−εn+δ]上的状态数。对于谐振子环境,可以得到
该分布在环境维数足够大的时候近似于正则吉布斯分布,其中温度为β=(N−1)[E−εn+κλn2]N−1/∑n[E−εn+κλn2]N−1。
上述模型说明,在系统加环境的波函数集合中,绝大多数纯态波函数给出的系统约化密度矩阵在热力学极限下都满足正则分布。其实,对于宇宙中一个足够小的子系统,当整个宇宙处于任意一个纯态时 (不必是等概率分布的混态),这个子系统几乎都近似地处于热平衡态。这种现象被称为“广义正则原理” (general canonical principle) 或“正则典型性” (canonical typicality)。这样就可以将量子统计力学完全建立在量子力学的基础之上。
在广义正则热化研究中,系统和环境之间的纠缠会扮演重要的角色。如果系统和环境处于简单的直积态上,约化后的系统状态不会是正则系综的Gibbs分布。因此,满足广义热化的状态一定是系统和环境之间的纠缠态。文献[72-74]研究的系统和环境之间无相互作用,而笔者团队的工作证明相互作用的出现使得等能壳层变形。在变形的等能壳层内,对环境取平均得到的系统约化密度矩阵不再是正则的,变形会使得在小系统的热化态上产生一个灰度因子[75],影响约化系统的温度。
广义正则热化的一个重要应用是解释黑洞非热辐射谱和黑洞信息丢失之谜。2000 年Parikh 和 Wilczek[76]利用隧穿理论得到小质量Schwarzschild黑洞的非平衡辐射谱。质量为M的黑洞辐射能量为ω的粒子后,质量M改变为M–ω会影响辐射后的时空度规,并直接影响再辐射的概率分布,导致非正则热态:
则辐射分布不仅与黑洞质量有关,还与辐射粒子本身的能量有关。后来蔡庆宇等[77,78]发现,这种非热分布实际上包含了辐射粒子之间的关联信息,可以用来解释黑洞信息丢失之谜。他们计算了能量分别为ω1和ω2的两次辐射之间的关联熵S(ω1:ω2)=8πω1ω2,其中单次辐射熵S(ω)=−lnΓ(ω)。这意味着从黑洞视界先后辐射出的粒子之间存在关联,关联大小正比于两个粒子的能量。在此基础上可以得到黑洞辐射的级联公式:
其中S(ω2|ω1)是条件辐射熵。可以证明,当黑洞完全辐射掉 (∑ωi = M) 时,辐射的关联熵就是原初的黑洞熵,S(ω1,ω2,⋯,ωn)=4πM2。因此,基于上述关联信息可以解决黑洞辐射中的信息丢失问题,即黑洞辐射丢失的信息完全转化为辐射粒子间的关联。
仔细分析蔡庆宇等[77]的开创性工作,本文两位作者意识到如此复杂的黑洞度规给出的辐射粒子之间关联方式居然都相同,平衡情况辐射的非正则形式一定与黑洞的时空几何无关。基于非正则热化的工作,他们与蔡庆宇合作,从黑洞的“一毛”定理出发,两次级联辐射 (先后能量为ω1和ω2) 和一次能量为ω1+ω2单辐射的等价性,一般地推导出了黑洞辐射的非正则分布Γ(ω)[78]。研究分析还把黑洞的自由度B和时空其他部分O考虑成为热化环境。假设整个宇宙处在一个纯态:
黑洞的状态即是ρB=TrO[|Ψ ⟩⟨Ψ |],根据前面广义热化的讨论可以知道黑洞的状态近似为一个热态。再把辐射本身当作研究热力学系统,根据广义正则热化的思想,就能一般地得到黑洞辐射能谱的非热分布[79]。这一研究表明,辐射-黑洞关联导致的黑洞非热辐射谱是有限系统统计的必然结果。
需要指出的是,系统加环境的整个态空间中,还存在一部分不满足正则典型性的状态。近些年来,关于本征态热化假说 (eigenstate thermalization hypothesis) 的研究[80,81] 探讨了系统如何从这部分不满足正则典型性的少数状态演化到满足正则典型性的状态,为有限系统热化问题的研究提供了崭新的思路。
热力学发展的另一个维度是时间变得有限。在传统的热力学的研究中,很少关注时间维度。例如,传统热力学循环中的等温过程通常是准静态过程、无法包含演化过程,传统教科书通常也不会提及等温过程中时变参数是按照如何的方式进行变化的。热力学循环既是热力学研究的开端,又是热力学的一个重要应用。热力学循环通过周期性过程从高温热源提取热能并将其部分转化为可以使用的能源,如机械能。以热力学循环为基础的热机引起了第一次工业革命。围绕热力学循环的研究,总结出了热力学三大定律。其中最为重要的热力学第二定律表明,热力学循环能量转化效率是有上限的,即Carnot效率,它是通过理想Carnot循环来实现的。
理想Carnot循环给出了所有热力学循环效率的基本限制,杜绝了一大类永动机的尝试,是热力学发展的里程碑。Carnot循环是建立在一组准静态过程基础上的热力学循环,其中在两个分别与高、低温热源接触的等温过程中,要无穷缓慢地操控气体体积,Carnot循环需要的时间原则上是无穷长,这使得理想Carnot循环的在单位时间内输出为零,即功率为零。然而,在实际的应用中,通常最大的需求是热力学过程有较大的输出功率,例如我国最新装机的石岛核电站的一个关键指标是装机功率。针对这一类问题,有限时间热力学应运而生,其核心目标是弥合理想的传统热力学理论和实际应用之间的鸿沟,并推动非平衡热力学的发展,对近平衡过程给出定量的结果。
有限时间热力学的发展肇始于核电能源的发展。在20世纪50年代,Yvon[82]针对核电循环得到了最大功率输出时的效率。1975年,针对有限时间的Carnot循环,Curzon和Ahlborn[83]利用恒定热力学流的假设,得到了后来广为人知的CA效率,ηCA=1−√(Tc/Th)。值得注意的是该效率不依赖于循环中物质的特性,具有相当的普适性,因而得到了广泛的关注,并在20世纪七八十年代引发了有限时间热力学研究的热潮[84,85]。
有限时间热力学过程通常伴随着额外熵 (即不可逆熵) 产生,时间越长额外熵产生越少。在近些年发展的低耗散模型[86]中,工作物质在两个有限时间等温过程中吸收的热量表达成如下:
其中ΔS是系统从高温热源吸收热量带来的可逆熵变化,而Σh/τh和Σc/τc代表不可逆的熵产生。额外熵产生这种最简单的1/τ标度关系,通常被称为低耗散假设。值得注意的是,后来的很多模型采用这种标度假设,例如有限时间量子Carnot循环。基于低耗散模型,有限时间Carnot循环中功率输出为P=(Qh+Qc)/(τh+τc)。在功率最大 (∂P/∂τh=∂P/∂τc=0)时,该循环效率存在一个上限ηEMP=ηC/(2−ηC),即最大功率效率,它不依赖做功物质性质。值得强调的是,这个最大功率效率可以在Σh≫Σc时得到。
对于任意给定的输出功率P,有限时间Carnot循环的效率不仅存在上限,而且还存在下限。我们[87]推导出一般得到效率和功率约束关系:
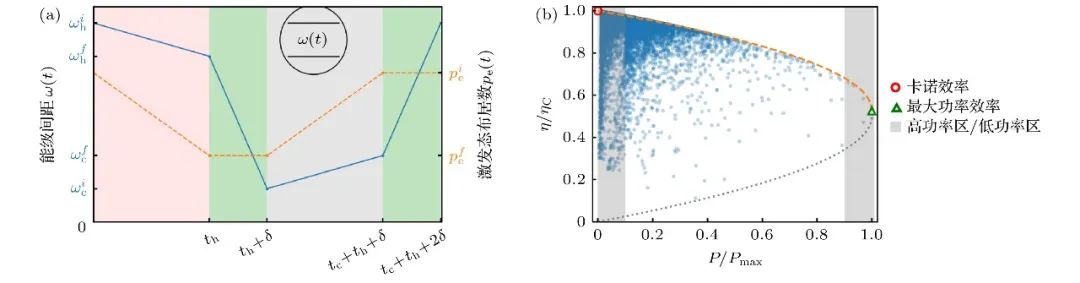
其中η̃=η/ηC和P̃=P/Pmax分别是以ηC和Pmax为单位的约化效率和功率。这个功率效率约束关系是一个不依赖于工作物质的普适关系,对任意情况成立。此前 Ryabov和Holubec[88,89]给出的近似的约束关系仅仅对P̃≈0和P̃≈1范围成立。图10展示了上述约束关系,其中蓝点代表以二能级原子为工作物质的热力学循环的功率和效率,红线和灰线分别代表了约束关系的上限和下限。图10说明利用低耗散1/τ假设得到的约束关系对于量子热力学循环同样适用。
图10 有限时间Carnot循环的功率效率约束关系 (a)基于二能级系统的有限时间量子Carnot循环;(b)量子Carnot循环中功率-效率和一般约束关系的对比,其中图中的棕色虚线和灰色点线是由(25)式给出,绿色三角代表最大功率的位置
在传统的准静态热力学循环中Carnot循环的效率最高,但在有限时间热力学过程中该结论不再成立。可以证明,在二者都在最大功率条件下,Otto循环的效率在一些参数区间内会明显优于Carnot循环。特别在温差较小的情况下,通过Otto热力学循环更容易获得更高的效率[90,91]。
低耗散模型之所以能在近些年掀起有限时间热力学研究的新潮流,是因为此模型能够把外界的控制方式和动力学演化纳入热力学研究的框架中[92]。在有限时间等温过程中,与不可逆熵产生关联的参数Σh和Σc与控制的过程直接相关。对于二能级量子系统,参数Σh=Θξ,其中Θ=βh2(ωhf−ωhi)2/8与系统初末状态参数以及环境温度有关,ξ=⟨v2⟩/⟨v⟩2与参数控制速度v的涨落相关。此后,有更多的研究将热力学过程控制纳入有限时间热力学的研究中,其中蕴含了后文提及的热力学长度等概念。
有限时间热力学的研究取得了大量的研究成果,它们在很大程度上使用了前述的低耗散模型假设,即不可逆熵的1/τ标度关系。在物理上,低耗散模型和热力学系统线性相应理论是等价的,因此1/τ标度关系是长时近似的结果[93]。有限时间热力学的理论和实验必须关注该标度关系在多大范围内适用。其实近期理论上有很多的研究从运动方程出发,给出了标度关系的成立区间,但是在实验上却鲜有这方面的研究成果,究其原因是实验平台的缺乏。最近,在一些微观实验的平台上[20],已有少数实验开始关注有限时间热力学。
3年前,我们[94]基于理想气体搭建了一个有限时间热力学实验平台。实验装置中的工作物质是干燥空气,其状态由理想气体状态方程描述。有限时间热力学过程通过步进电机进行精确控制。对于理想气体而言,一旦获得气体的压强P和体积V,就可以计算出气体的温度T,进而获得气体的内能变化。
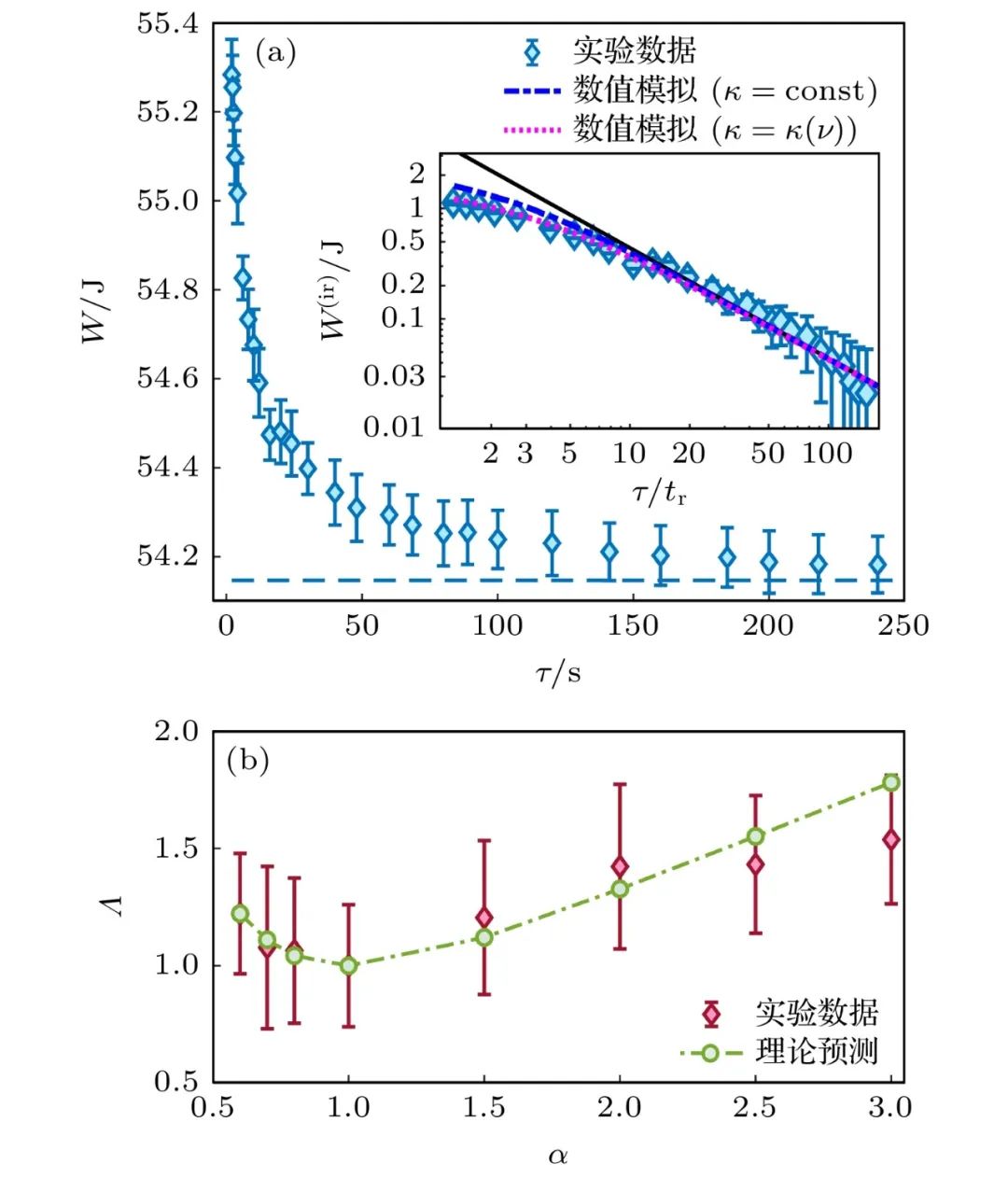
通常可以用不可逆做功来度量有限时间过程的不可逆性,Wirr(τ)=W(τ)−ΔF,其中ΔF是系统的自由能的变化。当操控速度V˙/V远大于气体的弛豫速率,即 (γ−1)trV˙/V≪1,不可逆做功也具有1/τ关系。其中γ是气体的绝热系数,tr是气体的热弛豫的特征时间。图11展示了在温度为50 ℃下压缩理想气体做功随过程时间τ的变化关系,实验数据证实,长时间可逆做功随时间按照1/τ标度关系衰减;不可逆熵做功可以通过压缩空气的方式来改变,在时间一定的情况下,匀速地压缩过程中不可逆做功明显低于以多项式方式压缩气体的做功。这个结果表明,有限时间热力学过程的操纵方式对于调节热力学过程十分重要。因此,这个研究工作为优化热能源转化过程提供了新思路。
图11 有限时间热力学1/τ关系的实验验证 (a) 温度50 ℃下做功的1/τ标度关系;(b) 标度关系的系数对操控方式的依赖关系L(t)=L0∝tα,能量损耗最优操控是匀速控制α=1
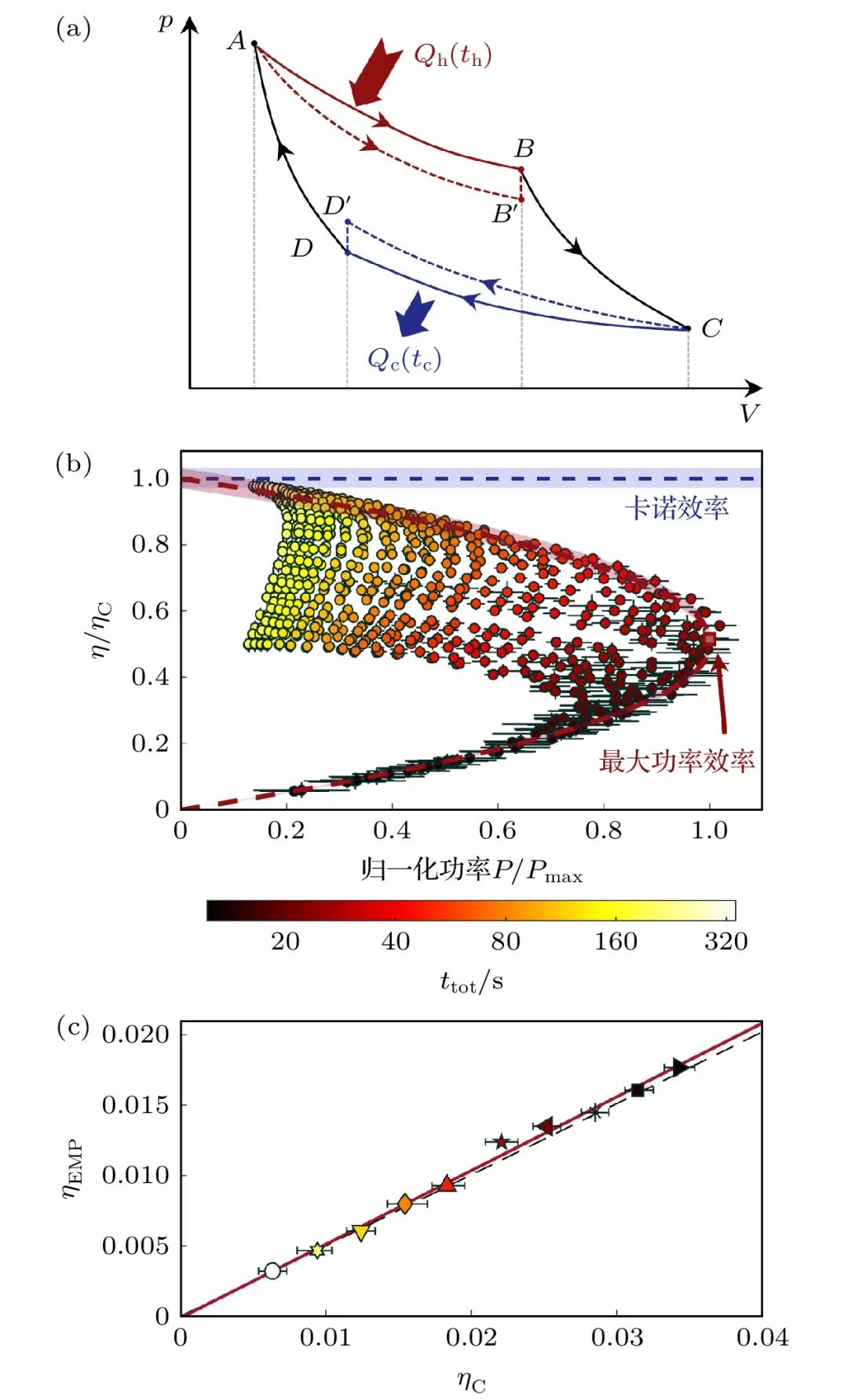
近些年热力学实验的一个重要方向[95-97]是验证有限时间热力学循环过程的功率和效率约束关系。基于搭建的理想气体的有限时间热力学平台,我们[98]设计完整的有限时间Carnot循环,并定量地验证了功率-效率约束关系。循环中两个等温过程分别在不同的温度的热浴中完成,在测得相应的做功和吸放热的同时,保证了等温过程的末态和另一个等温过程的初态通过一个绝热过程连接起来,实现了有限时间Carnot循环。图12展示了有限时间Carnot循环的过程和热力学循环的功率-效率约束关系。评估有限时间Carnot循环的关键量是最大功率效率。我们提取了实验中所有温度组合的最大功率效率,并在图12(c)中展示其与Carnot效率的关系。获得的最大效率 (带有误差棒的标记) 遵循一个简单的关系ηEMP = (0.524 ± 0.034)ηC。它与各种有限时间循环模型的最大功率效率在Carnot效率ηC的一阶项上很好地符合。例如,在CA模型中ηCA和低耗散模型[86]的ηC/(2−ηC)中,系数1/2是一个独立于特定特征的线性响应区域的普遍值[99]。我们的实验数据精确地确认了1/2系数的存在。
图12 有限时间Carnot循环 (a)有限时间Carnot循环的工作示意图;(b)循环中功率-效率约束关系;(c)最大功率效率对Carnot效率的依赖关系ηEMP = (0.524 ± 0.034)ηC
如前文所述,在有限时间热力学过程中,产生的不可逆性是评估热力学过程非平衡的一个重要指标。通常可以使用不可逆熵产生来衡量,例如在一个热化的过程中,不可逆的熵产生随时间单调递增。低耗散模型假设在热交换过程中不可逆熵的变化满足1/τ标度关系。对于直接可测量物理量,不可逆做功也存在1/τ标度关系。传统热力学和统计物理的研究表明,非准静态过程对体系做功会超过体系的自由能变化,即W⩾ΔF。近年有限时间热力学研究把此不等式替换成一个定量的关系W =ΔF+C/τ,其中C⩾0是与系统初末态以及操控方式有关的参数[32]。
事实上,上述定量的关系在有限时间热力学过程研究中至关重要,它牵涉到一个控制过程中时间和能量损耗的制约关系,必然涉及二者之间的优化匹配问题。给定控制时间τ,我们关心的是在多大程度上能够减小能量损耗,以及相关的理论极限问题。这个问题研究可以追溯到早期关于平衡态热力学距离问题,即非平衡过程的能量损耗极小值怎么受限于平衡态空间的几何属性。对于缓慢调控 (但非准静态) 的等温过程,系统在演化过程中的每一个瞬间都接近于热平衡态,它可以近似地由一组系统的平衡态参数描述,比如系统的压强和温度。在这样近平衡区域的近似下,不可逆程度将普适地反比于调控时间,可以通过几何的语言描述,这就导致了热力学长度的概念[100]。在几何上[101,102],热力学“距离”有明确的物理意义:在近平衡的缓慢驱动下,初末态间的热力学长度给出了在有限时间内完成等温过程所消耗的不可逆功下限[103-106]。
为简单起见,以理想气体为例,说明平衡态空间距离和非平衡过程不可逆性之间有特定的约束关系。束缚在一个体积为V的理想气体的相空间分布满足Maxwell分布。对于体积不同 (Vi和Vf) 的两个分布,通过Fisher信息度规gVV定义两个分布之间的距离:
再考虑温度为Te的环境中理想气体,从Vi变到Vf,在慢速控制下的不可逆功为
其中CV是等容比热,γ是热传导系数。利用变分原理可以得到在V˙/V=Const时,不可逆做功达到最小值,即Wirr,min∝D2。从这个简单的例子看出,最小不可逆做功和平衡态分布的距离有关,以下将对一类热力学过程[107]精确给出这种联系。
为了评估平衡热力学系统中特定控制参数的影响,要保证系统在参数调控完成之后仍然处在平衡状态上。这个过程是一个等温过程,在理论和实际应用中都至关重要。然而,实现等温过程的传统方案是准静态过程,因此需要无限长的驱动时间。当评估的时间小于系统弛豫时间,传统调控弛豫的方案无法使用。因此加速系统演化并保证系统参数调控完成之后达到平衡态是有限时间热力学中的挑战性问题。接下来一个非常自然而又与应用紧密相关的问题是:是否能够构造一种方案,加速实现等温过程,在有限时间内将系统从一个平衡态快速转换到另一个等温平衡态?等温捷径 (shortcuts to isothermality) 的方法就是一种加速等温过程的手段,实现等温平衡态之间的有限速率转换[108]。
考虑一个物理系统,其哈密顿量为 Ho(x,p,λ)=∑ipi2/2+Uo(x,p,λ)。我们希望施加辅助控制Ha(x,p,t)=λ˙⋅f(x,p,λ),使得在给定的时间τ,把参数λ从λi调控到λf下,并保持系统始终处在热平衡态上。此时系统拓展为由新哈密顿量H0+Ha描述的新系统。在起始和末了时刻,将辅助势场Ha(t)撤除,Ha(0)=Ha(τ)=0。这样使得扩展系统的哈密顿量 H0+Ha结束时恰好回到原来的哈密顿量H0。同时在初始和末了时刻,系统分布函数恰好就是相应哈密顿量对应的平衡态。在这个过程中,不可逆做功写成严格的二次型形式:
此时定义描述不可逆做功的度规为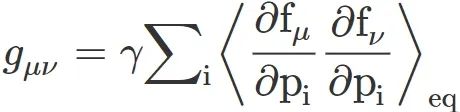 ,可以证明该度规是正定的。根据Cauchy-Schwarz不等式,最小不可逆功是
,可以证明该度规是正定的。根据Cauchy-Schwarz不等式,最小不可逆功是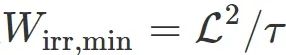 ,其中
,其中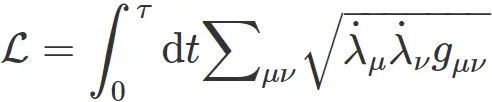 是两平衡态间的距离,即热力学长度。
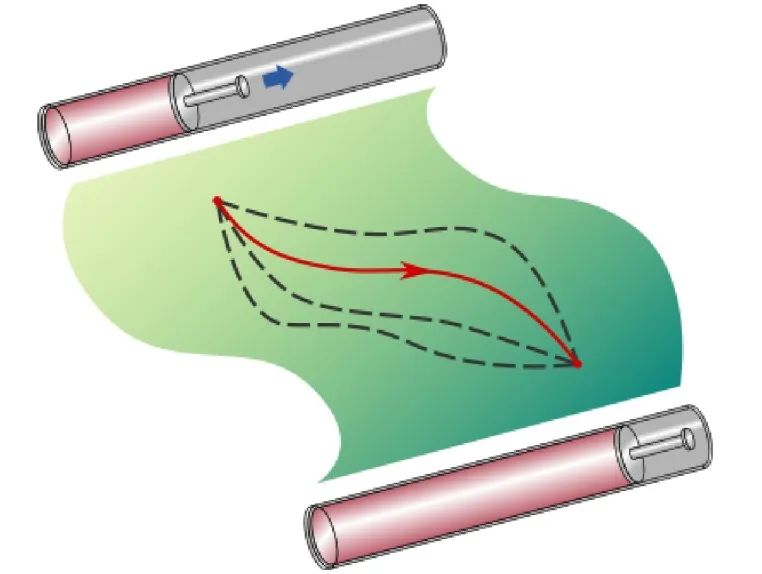
值得指出的是,热力学长度包含了一些动力学的参数,但与动力学过程无关,不依赖于参数的具体控制方式。在这一数学框架下,寻找能量消耗最小的优化控制方案等价于求解黎曼几何空间中的测地线方程 (如图13所示)。于是,就可以利用微分几何学的方法求解热力学中的最优控制问题,比如,利用捷径方法优化布朗热机的功率[109]。需要提及的是,最近也有一些研究中定义了依赖于时间的“度规”,当然不具有严格的空间几何属性[110]。
建立热力学长度和非平衡过程不可逆性之间的联系,是有限时间热力学中近些年的一个重要进展,它把传统热力学的做功和自由能关系W⩾ΔF拓展为W⩾ΔF+L2/τ,使得人们能够通过热力学长度找到能量损耗的下限,通过寻找几何测地线则能找到达到下限的操控方式。目前,研究热力学的几何方法已经被用来设计优化能量使用的具体方案[111-115],如用热力学几何构造信息擦除[111-113]和膜分离气体[114,115]的最小能量损耗方案。
是两平衡态间的距离,即热力学长度。
值得指出的是,热力学长度包含了一些动力学的参数,但与动力学过程无关,不依赖于参数的具体控制方式。在这一数学框架下,寻找能量消耗最小的优化控制方案等价于求解黎曼几何空间中的测地线方程 (如图13所示)。于是,就可以利用微分几何学的方法求解热力学中的最优控制问题,比如,利用捷径方法优化布朗热机的功率[109]。需要提及的是,最近也有一些研究中定义了依赖于时间的“度规”,当然不具有严格的空间几何属性[110]。
建立热力学长度和非平衡过程不可逆性之间的联系,是有限时间热力学中近些年的一个重要进展,它把传统热力学的做功和自由能关系W⩾ΔF拓展为W⩾ΔF+L2/τ,使得人们能够通过热力学长度找到能量损耗的下限,通过寻找几何测地线则能找到达到下限的操控方式。目前,研究热力学的几何方法已经被用来设计优化能量使用的具体方案[111-115],如用热力学几何构造信息擦除[111-113]和膜分离气体[114,115]的最小能量损耗方案。
总而言之,时空尺度有限的小系统统计物理和热力学研究已经成当代物理发展的重要前沿领域,它整体上可以用本文介绍的介观统计热力学进行概括和总结。其中,作为热力学第二定律的“升级版”,涨落定理 (由此可以推导出热力学第二定律) 是研究各种问题的关键,而有限系统的非正则平衡分布则内置了二阶涨落。
介观统计热力学与量子物理,能源物理以及信息科学结合,催生了一些重要的研究分支。这方面研究结果不仅丰富了统计热力学的内涵,而且为建立一般性的远离平衡的统计热力学理论框架带来了新的启示。这方面研究结果还可以应用到能源的产生与转化以及光合作用的应用领域。我们相信,未来介观统计热力学的发展将会在一些重大科学问题上取得突破,逐步走向实验和实际应用。
[1] Scovil H E D, Schulz-DuBois E O 1959 Phys. Rev. Lett. 2 262
[2] Geusic J E, Schulz-DuBios E O, Scovil H E D 1967 Phys. Rev. 156 343
[3] Alicki R 1979 J. Phys. A: Math. Gen. 12 L103
[4] Kosloff R 2013 Entropy 15 2100
[5] Kieu T D 2004 Phys. Rev. Lett. 93 140403
[6] Kieu T D 2006 Eur. Phys. J. D 39 115
[7] Scully M O 2003 Science 299 862
[8] Quan H T, Zhang P, Sun C P 2006 Phys. Rev. E 73 036122
[9] Quan H T, Liu Y xi, Sun C P, Nori F 2007 Phys. Rev. E 76 031105
[10] Binder F, Correa L A, Gogolin C, Anders J, Adesso G 2018 Thermodynamics in the Quantum Regime: Fundamental Aspects and New Directions (Cham: Springer International Publishing)
[11] Callen H B 1985 Thermodynamics and An Introduction to Thermostatistics (2nd Ed.) (New York: J. Wiley & Sons)
[12] Schrödinger E 1989 Statistical Thermodynamics (New York: Dover Publications)
[13] Reif F 2009 Fundamentals of Statistical and Thermal Physics (Waveland Press)
[14] Hill T L 2013 Thermodynamics of Small Systems (New York: Dover Publications, Inc)
[15] Allahverdyan A E, Serral Gracià R, Nieuwenhuizen Th M 2005 Phys. Rev. E 71 046106
[16] Leff H S, Rex A F 2003 Maxwell’s Demon 2: Entropy, Classical and Quantum Information, Computing (Philadelphia: Institute of Physics)
[17] Szilard L 1929 Z. Physik 53 840
[18] Landauer R 1961 IBM J. Res. Dev. 5 183
[19] Bennett C H 1982 Int. J. Theor. Phys. 21 905
[20] Bérut A, Arakelyan A, Petrosyan A, Ciliberto S, Dillenschneider R, Lutz E 2012 Nature 483 187
[21] Parrondo J M R, Horowitz J M, Sagawa T 2015 Nat. Phys. 11 131
[22] Quan H T, Wang Y D, Liu Y xi, Sun C P, Nori F 2006 Phys. Rev. Lett. 97 180402
[23] Sun C P, Quan H T 2013 Physics 42 756 (in Chinese) [孙昌璞, 全海涛 2013 物理 42 756]
[24] Dong H, Xu D Z, Cai C Y, Sun C P 2011 Phys. Rev. E 83 061108
[25] Cai C Y, Dong H, Sun C P 2012 Phys. Rev. E 85 031114
[26] Mandal D, Quan H T, Jarzynski C 2013 Phys. Rev. Lett. 111 030602
[27] Sekimoto K 1997 J. Phys. Soc. Jpn. 66 1234
[28] Jarzynski C 1997 Phys. Rev. Lett. 78 2690
[29] Jarzynski C 2011 Annu. Rev. Condens. Matter Phys. 2 329
[30] Jarzynski C 1997 Phys. Rev. E 56 5018
[31] Sekimoto K 1998 Prog. Theor. Phys. Suppl. 130 17
[32] Seifert U 2012 Rep. Prog. Phys. 75 126001
[33] Oono Y, Paniconi M 1998 Prog. Theor. Phys. Suppl. 130 29
[34] Hatano T, Sasa S ichi 2001 Phys. Rev. Lett. 86 3463
[35] Sekimoto K 2010 Stochastic Energetics (Berlin Heidelberg: Springer)
[36] Jiang D Q, Qian M, Qian M P 2004 Mathematical Theory of Nonequilibrium Steady States: On the Frontier of Probability and Dynamical Systems (Berlin: Springer)
[37] Esposito M, van den Broeck C 2010 Phys. Rev. Lett. 104 090601
[38] Kim K H, Qian H 2004 Phys. Rev. Lett. 93 120602
[39] Ge J 2014 Adv. Math. 43 161 (in Chinese) [葛颢 2014 数学进展 43 161]
[40] Jarzynskia C 2008 Eur. Phys. J. B 64 331
[41] Liphardt J, Dumont S, Smith S B, Tinoco I, Bustamante C 2002 Science 296 1832
[42] Collin D, Ritort F, Jarzynski C, Smith S B, Tinoco I, Bustamante C 2005 Nature 437 231
[43] Crooks G E 1999 Phys. Rev. E 60 2721
[44] Hummer G, Szabo A 2001 Proc. Natl. Acad. Sci. USA 98 3658
[45] Jarzynski C 2000 J. Stat. Phys. 98 77
[46] Maragakis P, Spichty M, Karplus M 2008 J. Phys. Chem. B 112 6168
[47] Hoang T M, Pan R, Ahn J, Bang J, Quan H T, Li T 2018 Phys. Rev. Lett. 120 080602
[48] Jarzynski C, Wójcik D K 2004 Phys. Rev. Lett. 92 230602
[49] Chen J F, Quan H T 2023 Phys. Rev. E 107 024135
[50] Evans D J, Cohen E G D, Morriss G P 1993 Phys. Rev. Lett. 71 2401
[51] Evans D J, Searles D J 1994 Phys. Rev. E 50 1645
[52] Gallavotti G, Cohen E G D 1995 Phys. Rev. Lett. 74 2694
[53] Gallavotti G, Cohen E G D 1995 J. Stat. Phys. 80 931
[54] Barato A C, Seifert U 2015 Phys. Rev. Lett. 114 158101
[55] Timpanaro A M, Guarnieri G, Goold J, Landi G T 2019 Phys. Rev. Lett. 123 090604
[56] Kurchan J 2000 A Quantum Fluctuation Theorem (arXiv:cond-mat/0007360)
[57] Tasaki H 2000 Jarzynski Relations for Quantum Systems and Some Applications (arXiv: cond-mat/0009244)
[58] Talkner P, Lutz E, Hänggi P 2007 Phys. Rev. E 75 050102
[59] Dorner R, Clark S R, Heaney L, Fazio R, Goold J, Vedral V 2013 Phys. Rev. Lett. 110 230601
[60] Mazzola L, De Chiara G, Paternostro M 2013 Phys. Rev. Lett. 110 230602
[61] Batalhão T B, Souza A M, Mazzola L, Auccaise R, Sarthour R S, Oliveira I S, Goold J, De Chiara G, Paternostro M, Serra R M 2014 Phys. Rev. Lett. 113 140601
[62] An S, Zhang J N, Um M, Lv D, Lu Y, Zhang J, Yin Z Q, Quan H T, Kim K 2015 Nat. Phys. 11 193
[63] Jarzynski C, Quan H T, Rahav S 2015 Phys. Rev. X 5 031038
[64] Funo K, Quan H T 2018 Phys. Rev. Lett. 121 040602
[65] Gong Z, Lan Y, Quan H T 2016 Phys. Rev. Lett. 117 180603
[66] Fei Z, Zhang J, Pan R, Qiu T, Quan H T 2019 Phys. Rev. A 99 052508
[67] Fei Z, Quan H T 2020 Phys. Rev. Lett. 124 240603
[68] Funo K, Quan H T 2018 Phys. Rev. E 98 012113
[69] Chen J F, Qiu T, Quan H T 2021 Entropy 23 1602
[70] Wang B, Zhang J, Quan H T 2018 Phys. Rev. E 97 052136
[71] Chen J, Dong H, Sun C P 2018 Phys. Rev. E 98 062119
[72] Tasaki H 1998 Phys. Rev. Lett. 80 1373
[73] Goldstein S, Lebowitz J L, Tumulka R, Zanghì N 2006 Phys. Rev. Lett. 96 050403
[74] Popescu S, Short A J, Winter A 2006 Nat. Phys. 2 754
[75] Dong H, Yang S, Liu X F, Sun C P 2007 Phys. Rev. A 76 044104
[76] Parikh M K, Wilczek F 2000 Phys. Rev. Lett. 85 5042
[77] Zhang B, Cai Q Y, You L, Zhan M S 2009 Phys. Lett. B 675 98
[78] Dong H, Cai Q Y, Liu X F, Sun C P 2014 Commun. Theor. Phys. 61 289
[79] Ma Y H, Cai Q Y, Dong H, Sun C P 2018 EPL 122 30001
[80] Srednicki M 1994 Phys. Rev. E 50 888
[81] D’Alessio L, Kafri Y, Polkovnikov A, Rigol M 2016 Adv. Phys. 65 239
[82] Yvon J 1955 Proceedings of the International Conference on the Peaceful Uses of Atomic Energy Geneva, Switzerland, August 8—20, 1955
[83] Curzon F L, Ahlborn B 1975 Am. J. Phys. 43 22
[84] Andresen B, Salamon P, Berry R S 1984 Phys. Today 37 62
[85] Chen J C, Su S H, Su G Z 2023 Reflection and Exploration on Hot Issues in Thermodynamics and Statistical Physics (2nd Ed.) (Beijing: Science Press) (in Chinese)[陈金灿, 苏山河, 苏国珍 2023 热力学与统计物理学热点问题思考与探索(第二版)(北京: 科学出版社)
[86] Esposito M, Kawai R, Lindenberg K, Van den Broeck C 2010 Phys. Rev. Lett. 105 150603
[87] Ma Y H, Xu D, Dong H, Sun C P 2018 Phys. Rev. E 98 042112
[88] Ryabov A, Holubec V 2016 Phys. Rev. E 93 050101
[89] Long R, Liu W 2016 Phys. Rev. E 94 052114
[90] Chen J F, Sun C P, Dong H 2019 Phys. Rev. E 100 062140
[91] Chen J F, Sun C P, Dong H 2019 Phys. Rev. E 100 032144
[92] Ma Y H, Xu D, Dong H, Sun C P 2018 Phys. Rev. E 98 022133
[93] Cavina V, Mari A, Giovannetti V 2017 Phys. Rev. Lett. 119 050601
[94] Ma Y H, Zhai R X, Chen J, Sun C P, Dong H 2020 Phys. Rev. Lett. 125 210601
[95] Blickle V, Bechinger C 2012 Nat. Phys. 8 143
[96] Roßnagel J, Dawkins S T, Tolazzi K N, Abah O, Lutz E, Schmidt-Kaler F, Singer K 2016 Science 352 325
[97] Martínez I A, Roldán É, Dinis L, Petrov D, Parrondo J M R, Rica R A 2016 Nat. Phys. 12 67
[98] Zhai R X, Cui F M, Ma Y H, Sun C P, Dong H 2023 Phys. Rev. E 107 L042101
[99] Tu Z C 2021 Front. Phys. 16 33202
[100] Salamon P, Berry R S 1983 Phys. Rev. Lett. 51 1127
[101] Weinhold F 1975 J. Chem. Phys. 63 2479
[102] Ruppeiner G 1979 Phys. Rev. A 20 1608
[103] Crooks G E 2007 Phys. Rev. Lett. 99 100602
[104] Scandi M, Perarnau-Llobet M 2019 Quantum 3 197
[105] Abiuso P, Miller H J D, Perarnau-Llobet M, Scandi M 2020 Entropy 22 1076
[106] Chen J F, Sun C P, Dong H 2021 Phys. Rev. E 104 034117
[107] Li G, Chen J F, Sun C P, Dong H 2022 Phys. Rev. Lett. 128 230603
[108] Li G, Quan H T, Tu Z C 2017 Phys. Rev. E 96 012144
[109] Chen J F 2022 Phys. Rev. E 106 054108
[110] Van Vu T, Hasegawa Y 2021 Phys. Rev. Lett. 126 010601
[111] Dago S, Pereda J, Barros N, Ciliberto S, Bellon L 2021 Phys. Rev. Lett. 126 170601
[112] Zhen Y Z, Egloff D, Modi K, Dahlsten O 2021 Phys. Rev. Lett. 127 190602
[113] Ma Y H, Chen J F, Sun C P, Dong H 2022 Phys. Rev. E 106 034112
[114] Tsirlin A M, Kazakov V, Zubov D V 2002 J. Phys. Chem. A 106 10926
[115] Chen J F, Zhai R X, Sun C P, Dong H 2023 PRX Energy 2 033003
2024年诺贝尔物理学奖授予人工神经网络,这是一场统计物理引发的机器学习革命。统计物理学不仅能解释热学现象,还能帮助我们理解从微观粒子到宏观宇宙的各个层级如何联系起来,复杂现象如何涌现。它通过研究大量粒子的集体行为,成功地将微观世界的随机性与宏观世界的确定性联系起来,为我们理解自然界提供了强大的工具,也为机器学习和人工智能领域的发展提供了重要推动力。
为了深入探索统计物理前沿进展,集智俱乐部联合西湖大学理学院及交叉科学中心讲席教授汤雷翰、纽约州立大学石溪分校化学和物理学系教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学物理系助理教授唐乾元,以及多位国内外知名学者共同发起「非平衡统计物理」读书会。读书会旨在探讨统计物理学的最新理论突破,统计物理在复杂系统和生命科学中的应用,以及与机器学习等前沿领域的交叉研究。读书会从12月12日开始,每周四晚20:00-22:00进行,持续时间预计12周。我们诚挚邀请各位朋友参与讨论交流,一起探索爱因斯坦眼中的普适理论!
详情请见:从热力学、生命到人工智能的统计物理之路:非平衡统计物理读书会启动!
推荐阅读
9. 加入集智,一起复杂!
点击“阅读原文”,报名读书会