导语


内在维度（Intrinsic Dimension）是表征学习中用于表示一个系统或一个状态时所需要的最小维度。在力学语境下描述运动时，这一概念与物理系统的自由度（degree of freedom）类似，可以用于表征一个系统时所需要的最小坐标维度。当坐标系处于表征该物理系统的最小表示维度时，其数学模型往往是简洁且意义清晰的。近日，清华大学地球系统科学系黄小猛教授课题组发表于人工智能顶级会议 KDD 2024 上的一项研究，探究了如何计算用于表征物理动力演化的算子在潜空间下的内在维度，并揭示了在内在维度下神经网络结构能更准确地建模物理动力。根据这一理论，该研究提出了一种名为神经流形算子（Neural Manifold Operators）的模型，能够精确建模受多种方程控制的物理动力和真实世界的物理动力。由于对物理系统进行内在维度表征，该模型在实现高精度建模的同时，也实现了轻量化和物理一致性等优点。


关键词：计算物理，流形学习，神经算子，表征学习

熊巍 | 作者



论文题目：Neural Manifold Operators for Learning the Evolution of Physical Dynamics

论文链接：https://dl.acm.org/doi/10.1145/3637528.3671779

代码链接：https://github.com/AI4EarthLab/Neural-Manifold-Operators





前言




对物理动力学演化的准确建模是研究和预测物理系统的基础，在科学和工程中是一项普遍的挑战。在以往的科学发展历史中，物理学家试图从第一性原理出发而推导出物理动力学的解析模型来研究物理系统的演化，使得建模的物理系统具备了可预测性。通过解析或数值方法，对这一数学模型求解来获得对该系统未来状态的预测，这种方法孕育了许多实际应用，例‍如数值天气预报等。然而，在现实场景中极高的自由度和复杂性使得物理模型的建立和求解依赖更多的近似假设条件和更高的计算成本。基于神经算子的物理动力建模方法孕育而生。


在数学中，描述 Banach 空间中映射的算子具有无‍限维的特性，因此，算子的维度表示成为算子学习建模物理动力演化的关键问题。‍‍以大气模型为例，在数值求解天气模型时连续的大气控制方程被精细的网格离散成数以万计个格点（若空间分辨率为10km级），则这一离散的大气系统的自由度就趋于1011，而这一自由度将随着分辨率的提高指数级增大。我们是否能够准确计算该系统的最‍优表示维‍度，并以此为基础设计神经网络结构来对其进行表征？近日发表于KDD 20‍24 的‍ Neural Manifold Operators（NMO）模型通过计算物理系统的内在维度，来实现对物理系统演化的最优表征。





什么是内在维度（Intrinsic Dimension）？




内在维度是描述数据或系统在低维空间中最本质表示的一种度量。它表示在不丢失信息的前提下，能够用来表征数据或系统的最小独立变量的数量。从神经网络视角下，内在维度可以看作是描述物理系统下的最小表示参数或维度；从动力系统视角下，内在维度可以类比成描述运动的最小自由度。


在冗余空间中，如果存在一个更低维的子流形（例如，在三维空间中的曲面或二维空间中的曲线），则可以通过其内在维度空间下的坐标去表示。这样构建的解析模型通常更为简洁，并且从拟合的视角看，需要被遍历的状态也更少。因此，如何准确估计未知系统的内在维度，是NMO 模型要解决的核心问题。





物理系统的内在维度如何计算？




NMO 模型通过构建自编码器和时间演化算子来模拟物理系统的动力学演化。该模型通过对物理系统在时间维度上的采样来驱动自编码器的训练，从而建立物理空间到高维冗余潜在空间的坐标映射。随后，通过极大似然估计来计算潜空间中用于表示潜在算子的最优子流形的内在维度。假设通过编解码器构建的潜空间是冗余的，目标的低维子流形在低维空间存在一个未知分布且其映射光滑，并满足局部密度假设，则可以通过最近邻算法计算这一维度



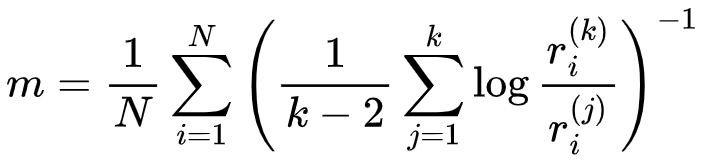
这一维度m被视为该系统在这一潜空间下的内在维度，用于确定 NMO 模型中时间演化算子模块的维度，从而学习物理系统的动力学演化。


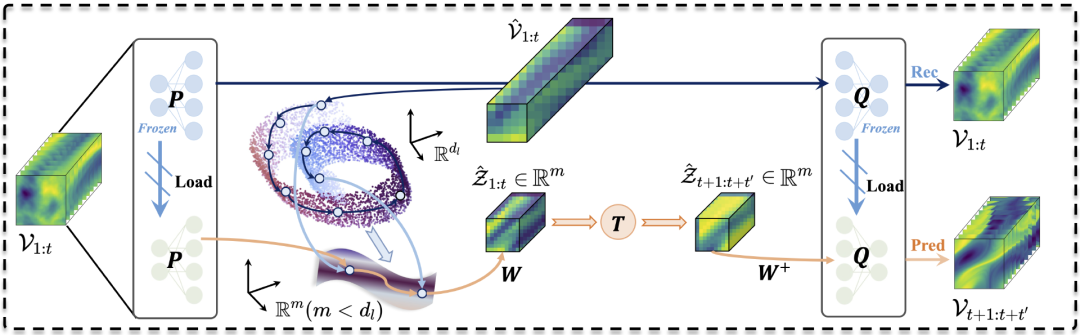
图1 NMO模型的结构示意图





使用内在维度学习目标算子的优势是什么？




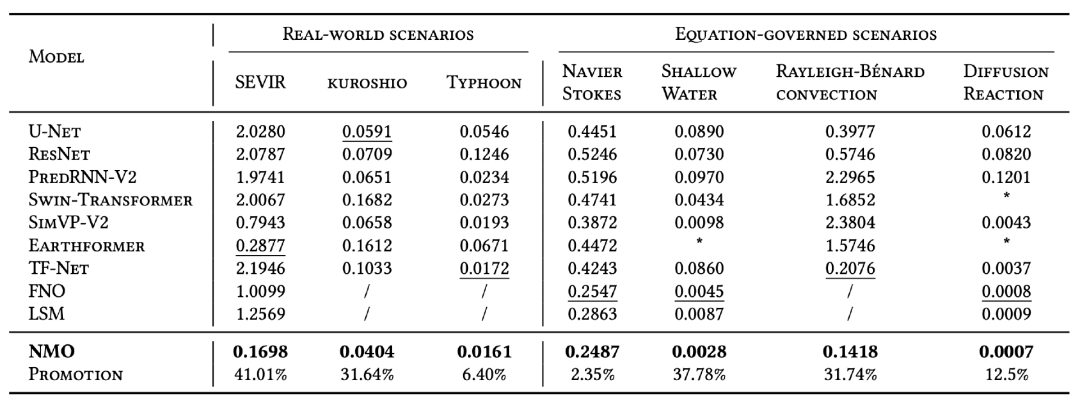
计算得到的内在维度m，在理论上应独立于模型的实现结构。为了验证模型在不同结构下的有效性，NMO模型分别尝试了基于全连接神经网络、卷积神经网络和Transformer架构实现的时间演化算子模块，由下表所示，在黑潮（一种海洋西边界洋流）和Navier-Stokes 系统下，各类结构均在内在维度m时呈现出最优效果。


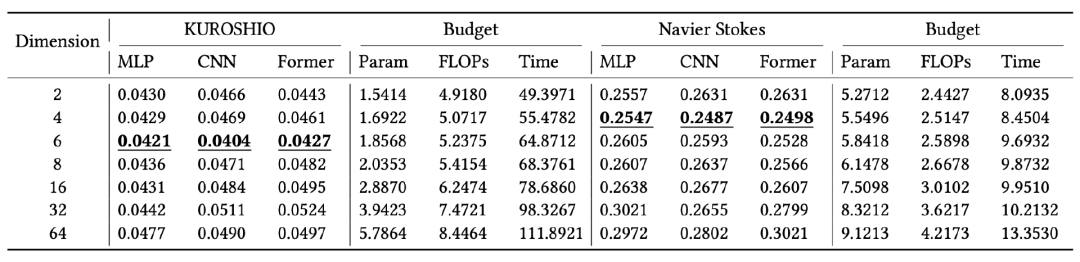
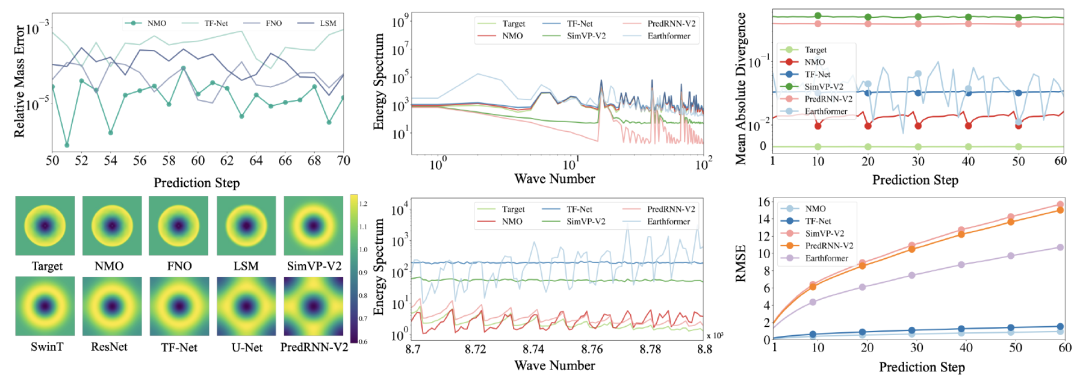
图2 对时间演化算子维度的研究，评估三种实现方式：多层感知机（MLP）、卷积神经网络（CNN）和Transformer结构（Former）。下划线标注了每种实现方式中准确率最高的情况，而加粗字体则表示各场景中的内在维度（ID）。Budget栏展示了各场景下的最优模型参数量（PARAM）、浮点运算量（FLOPs）和训练时间（TIME）。


经研究，使用内在维度表示的时间演化算子来学习目标物理系统的动力演化，主要具备以下优势（1）由于消除冗余维度后，模型结构更加轻量化，显著降低了计算时间和成本（见图 3）；（2）在未增加物理约束的情况下，该方法能够有效避免过拟合，并准确学习物理系统中的特定物理性质，如质量守恒等（见图4）；（3）与同类模型相比，无论是在真实世界场景还是在偏微分方程控制的场景下，该方法均实现了最优的建模效果（见图5）。


图3 各模型在SEVIR和Navier-Stokes方程场景下的训练时间及RMSE性能排名。


图4 左图：浅水方程场景中每个时间步的相对质量误差及各模型预测结果的可视化。中图：Rayleigh-Bénard对流场景中的湍流能谱。右图：Rayleigh-Bénard对流场景中每个时间步的平均绝对散度对流以及各模型预测步对应的RMSE。


图5 在所有场景中与9个Baseline模型进行性能比较。使用RMSE作为模型评估指标，RMSE值越小表示精度越高。由于FNO仅针对单变量预测设计，因此我们仅在单变量场景下评估这些模型，以确保基线模型的最佳性能。下划线表示基线模型中最准确的结果，加粗字体表示所有模型中最准确的结果。星号（*）表示GPU内存溢出（超过40GB），斜杠（/）表示原始模型仅设计用于单变量预测。


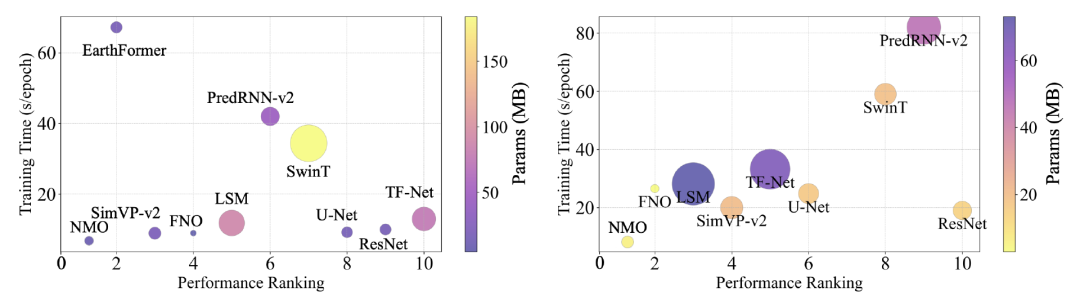
综上，NMO 模型从数学和实验的角度，尝试回答神经算子在学习潜在算子时，如何利用有限维参数空间对无限维算子进行参数化表示的问题，并为神经算子维度的选择提供了有效依据。



相关文献

[1] Wu H, Weng K, Zhou S, Huang X, Xiong W. Neural Manifold Operators for Learning the Evolution of Physical Dynamics. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining 2024 Aug 25 (pp. 3356-3366).

[2] Levina E, Bickel P. Maximum likelihood estimation of intrinsic dimension. Advances in neural information processing systems. 2004;17.



集智学园最新课程：

Koopman分析在非线性动力学中的应用


非线性动力学是复杂系统研究中重要的理论基础和研究工具，它有助于理解系统的本质特性，通过构建和分析系统的粗粒化程度不同的数学模型来解决实际问题。尽管低维非线性系统的理论已经相当完备，但如何将其用到高维非线性体系中，获取系统的关键动力学信息是一个长期困扰研究者的挑战。

好的理论和工具会大大加快科研进展，Koopman算符有望成为分析和预测动态系统的标准理论。集智学园邀请北京邮电大学兰岳恒教授开设「Koopman分析在非线性动力学中的应用」系列课程，面向致力于学习和发展Koopman算符理论的社区朋友，在6节课程时间中，通过细致的讲解，深入的互动，形成苏格拉底式课堂氛围，共同进步。欢迎感兴趣的朋友加入课程！


推荐阅读

1. 傅立叶神经算子：傅立叶变换应用于深度学习，顽强求解偏微分方程
2. 前沿进展：Koopman神经算子求解偏微分方程
3. Nat.Rev.Phys.观点：超越传统神经网络，神经算子加速科学仿真与设计
4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程
5. 龙年大运起，学习正当时！解锁集智全站内容，开启新年学习计划

6. 加入集智，一起复杂！



点击“阅读原文”，报名课程