一分钟数学:范畴论
导语
范畴论为在复杂的科学领域中表述和解决问题提供了一种形式化的抽象语言,来描述对象之间的相互作用。除了数学,范畴论的应用遍及神经科学、化学、生物学、集成电路、计算机科学甚至宇宙学。
研究领域:范畴论

Rachel | 作者
陈昊 | 译者
J-CAT | 审校
邓一雪 | 编辑
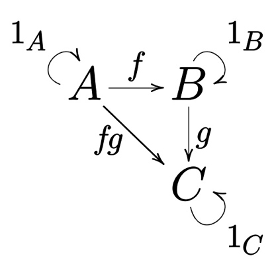
1. 必须存在一个恒等态射可以将一个对象映射到其自身,如图1所示范畴中的映射1A:A→A
2. 态射可以组合。如果存在两个态射f和g,f可以将A映射为B,g可以将B映射为C,则一定存在映射fg可以将A映射为C。
3. 恒等态射和一般态射的组合必须要满足单位律(unit law axiom),即如果有
4. 态射需要满足结合律,即(hg)f=h(gf)。
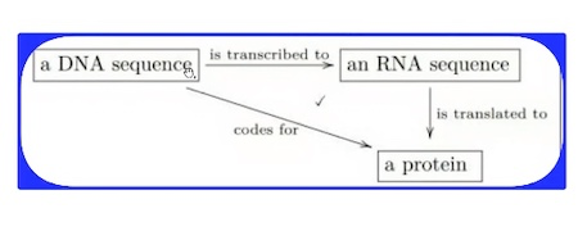
宇宙学中的范畴论
宇宙学中的范畴论
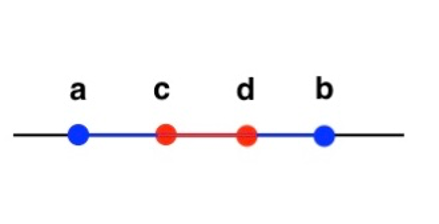
图3. 区间域的示例。实线上所有闭区间的集合,其顺序由逆集包含(reverse set inclusion)确定。例如,对于图中的闭区间[a,b]在区间域中的排序在闭区间[c,d]之前,因为[c,d]包含于[a,b]。
范畴论第二季报名中
范畴论是一个研究结构的理论,提供了一种系统、精确、抽象的跨领域科学方法论,可直接付诸于各领域考察的问题,寻求跨领域的解决之道。这种数学语言与复杂性科学有众多相似之处,加之其本身作为数学工具的严密性,后续可能能为解决复杂性科学问题提供一把钥匙。
为了让大家了解范畴论这样一门现代数学语言,克服传统学习范畴论抽象和对前置知识的障碍,集智学园特邀一位正在尝试教中学生范畴论的J-CAT猫圈老师开课,筹划了“集智范畴论入门系列课程”。第二季课程正式推出,在第一季习得的范畴论思维方式基础上,本季课程将站在新的起点上,更多关注范畴论内在的问题,而不用过于关注具体的问题背景。例如在范畴论中,可以直接抽象地讨论一个作为函子的箭头如何运动到另一个函子箭头,这样需要理解函子范畴和自然变换的概念。通过掌握这些越来越抽象的思维工具,学员将逐渐感受到范畴论的强大抽象简化能力,感受到为何不同领域的研究前沿不约而同地应用这些工具。
人人可学的范畴论第一季——跨领域的科学方法论 | 精品入门系列课
推荐阅读
点击“阅读原文”,追踪复杂科学顶刊论文