什么是香农信源编码定理 | 集智百科

本词条由集智俱乐部众包生产,难免存在纰漏和问题,欢迎大家留言反馈或者前往对应的百科词条页面进行修改,一经修改,可以获得对应的积分奖励噢!
目录

在信息论中,香农信源编码定理 Shannon’s source coding theorem(或无噪声编码定理)建立了可能的数据压缩 data compression 的极限,以及香农熵 Shannon entropy的操作意义。
以克劳德·香农 Claude Shannon命名的信源编码定理表明,(在极限情况下,当独立的均匀分布的随机变量(i.i.d.)数据流的长度趋于无穷大时)不可能压缩数据使编码率(每个符号的平均比特数)小于信源的香农熵,而事实上又不能确定信息会丢失。然而,可以任意地使码率接近香农熵,损失的概率可以忽略不计。
符号码的信源编码定理根据输入单词(被视为一个随机变量)熵和目标字母表大小将最小可能期望码字长度作为一个函数,并设置了一个上下界。
说明
信源编码是从信源符号序列到字母符号序列(通常是比特)的映射,使信源符号能够准确地从二进制比特位(无损源编码)恢复或在某种失真(有损源编码)范围内恢复。这就是数据压缩的概念。
信源编码定理
在信息论中,信源编码定理(Shannon,1948)):
N i.i.d.每个随机变量都有熵 H(X)可以压缩成超过N H(X)。随着N → ∞,位的信息丢失风险可以忽略不计;但反过来说,如果它们被压缩成少于N H(X) 位,则信息肯定将丢失。
符号码的源码定理
令Σ1,Σ2表示两个有限字母,并让Σ1*和Σ2*分别表示这些字母中所有有限词的集合。
假设X是一个随机变量,取值在Σ1,让 f 是一个唯一可解码代码,从Σ1*到Σ2*,其中|Σ2|=a。让S表示由码字 f (X)的长度给出的随机变量。
如果 f 是最优的,因为它具有X的最小预期字长,则(Shannon 1948): X
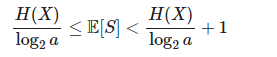
其中Ε表示期望值运算符。
证明:源代码定理
给定X是一个iid源,它的时间序列X1, …,Xn是 iid ,在离散值情况下熵H(X)和在连续值情况下微分熵。源编码定理指出,对于任何ε > 0,即对于大于源熵的任何速率H(X) + ε,有足够大的n和一个编码器,该编码器采用源的niid 重复,X1:n,并将其映射到n(H(X) + ε)个二进制位,使得源符号X1:n可以至少1 − ε.的概率从二进制位中恢复。
可实现性证明。修正一些ε > 0,让
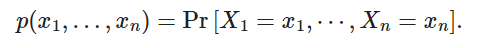
典型集,Anε 定义如下:
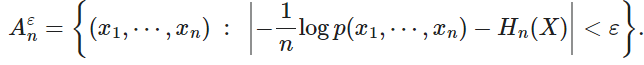
该渐近均分割性(AEP)示出了对于足够大n,使得由源在于典型的集合生成的序列的概率,Anε ,如定义接近一。特别是,对于足够大的n,P(X1,X2,,,,,Xn)∈Anε )可以任意接近 1,具体来说,大于1 − ε(有关证明,请参阅 AEP)。
典型集合的定义意味着那些位于典型集合中的序列满足:
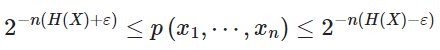
概率:
-
序列的概率(X1 ,X2,,,,,Xn)从A中抽取nε 大于1 − ε
-
|Anε |<=2n(H(X)+ε)从左侧(下限)得出p(x1,x2,,,xn)
-
|Anε |>=(1 − ε)2n(H(X)-ε),从上界得出p(x1,x2,,,xn)以及整个集合A的总概率的下界nε
编码算法:编码器检查输入序列是否在典型集合内;如果是,则输出输入序列在典型集合中的索引;如果不是,则编码器输出任意n(H(X) + ε)位数字。只要输入序列位于典型集合内(概率至少为 1 − ε), 位数字。只要输入序列位于典型集合内概率至少为ε为界。
Converse的证明:反过来证明,任何小于A的集合nε 在指数的意义上)将涵盖一组远离1的概率。
证明:符号代码的源编码定理
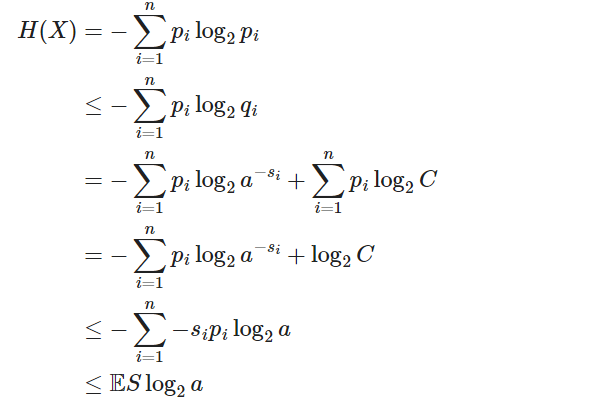

对于第二个不等式,我们可以设置
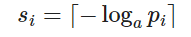
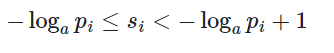

和
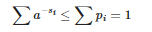
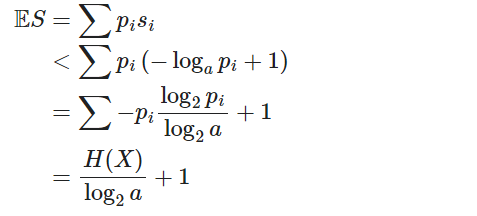
非平稳独立源的扩展
离散时间非平稳独立源的固定速率无损源编码
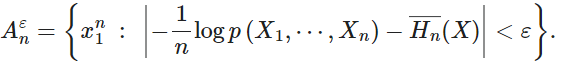
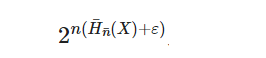

编者推荐

集智文章推荐
计算美学前沿速递:用信息论“重新发现”风景画艺术史
Science前沿:用信息论解释动植物间的军备竞赛
百科项目志愿者招募



在这里从复杂性知识出发与伙伴同行,同时我们希望有更多志愿者加入这个团队,使百科词条内容得到扩充,并为每位志愿者提供相应奖励与资源,建立个人主页与贡献记录,使其能够继续探索复杂世界。
如果你有意参与更加系统精细的分工,扫描二维码填写报名表,我们期待你的加入!

来源:集智百科
编辑:王建萍
-
热力学第二定律中的悖论 | 集智百科 -
什么是临界点 | 集智百科 -
什么是蒙特卡罗模拟 | 集智百科 -
什么是自组织临界控制 | 集智百科 -
《张江·复杂科学前沿27讲》完整上线! -
成为集智VIP,解锁全站课程/读书会
点击“阅读原文”,阅读词条香农信源编码定理原文与参考文献










