复杂性科学的机遇:2021年诺贝尔物理学奖解读

导语
2021年诺贝尔物理学奖授予三位科学家(图1),以表彰他们“对我们理解复杂物理系统的开创性贡献”。美籍日裔科学家真锅淑郎(Syukuro Manabe)、德国科学家克劳斯·哈塞尔曼(Klaus Hasselmann)因为“地球气候的物理建模,量化可变性并可靠地预测全球变暖”的研究共享了诺贝尔物理学奖的一半奖金;意大利科学家乔治·帕里西(Giorgio Parisi)因为“发现了从原子尺度到行星尺度物理系统中的无序和涨落的相互作用”而获得了诺贝尔物理学奖的另一半奖金。今年诺贝尔物理学奖授予复杂性科学领域,既说明该领域的研究已经获得学术界的重视,同时也为复杂系统研究的发展带来了新机遇。
关键词 诺贝尔物理学奖,气候变化,地球系统科学,无序系统,自旋玻璃

陈晓松 樊京芳(北京师范大学系统科学学院) | 作者
2022年第1期 | 来源
1. 复杂系统与复杂性科学
1. 复杂系统与复杂性科学

2. 地球气候复杂系统
2. 地球气候复杂系统
地球气候系统是一个典型的复杂自适应系统,从组成结构上来看主要包括:大气圈、水圈、冰冻圈、岩石圈和生物圈5大圈层。同时各个圈层之间和内部具有高度的非线性物理、化学、生物过程和反馈回路[4]。图2展示了一个地球气候复杂系统的示意图。当前研究地球气候系统主要有两种技术手段:(1)基于观测数据;(2)基于气候模式(climate models)。观测数据通常是指通过仪器(包括气象站或卫星)获得的数据、再分析(包括ECMWF、NCEP-NCAR和JRA)数据以及代理数据(包括珊瑚记录、树木年轮和冰芯记录等)。气候模式是试图模拟产生气候的5大圈层之间的物理、化学和生物过程,目前是理解和预测这些过程和相互作用的基本方法,被广泛应用于天气预报、理解气候、预测气候变化等方面。一般的气候模式建立包含复杂的动力及热力学过程和物理化学过程的数学模型,并基于历史或当前观测数据来模拟和预测气候系统的演化,不仅可以用来分析和理解一些气候现象及整个地球气候系统的物理学机制,还可以模拟和预测在气候变化背景下,气候系统的演化方向等。气候模式的开发通常依赖于经典物理学、计算数学、计算机和大气动力学的逐步发展和持续积累。真锅淑郎(Syukuro Manabe)和克劳斯·哈塞尔曼(Klaus Hasselmann)就是因“对地球气候的物理建模、量化可变性和可靠地预测全球变暖”而共同获得2021年诺贝尔物理学奖金的一半(图1)。
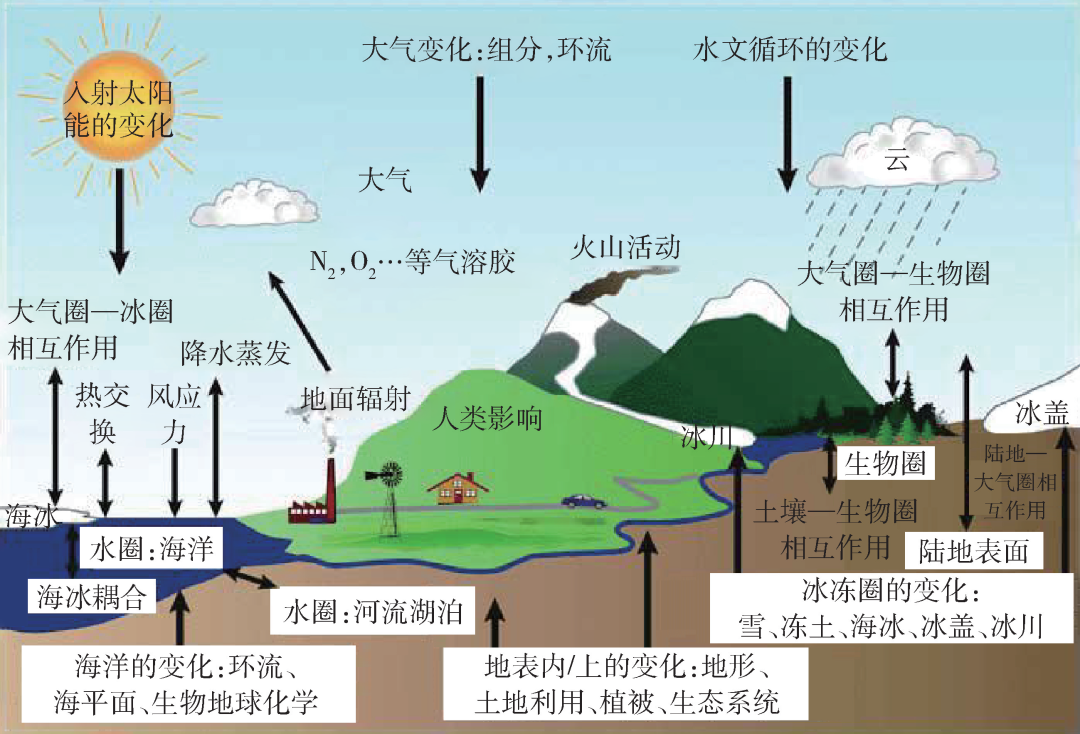
图2 地球复杂系统最基本的组成元素以及相互作用过程。图片来自于政府间气候变化专门委员会(IPCC)第四次评估报告[4]
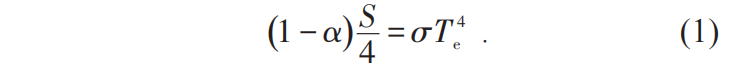
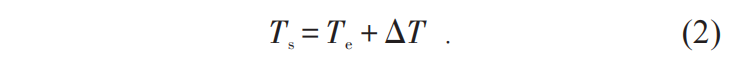
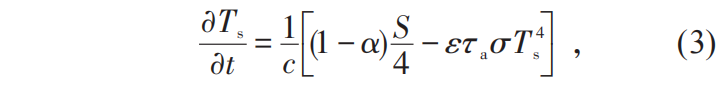
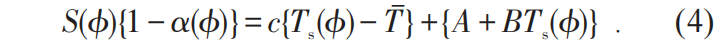
 代表的是全球平均地表温度;A和B是控制长波辐射损耗的参数(A=204.0 W·m-2,B=2.17 W·m-2·℃-1)。值得注意的是,在一些更为复杂的能量平衡模型中还会考虑大气和海洋之间的能量转移。
代表的是全球平均地表温度;A和B是控制长波辐射损耗的参数(A=204.0 W·m-2,B=2.17 W·m-2·℃-1)。值得注意的是,在一些更为复杂的能量平衡模型中还会考虑大气和海洋之间的能量转移。
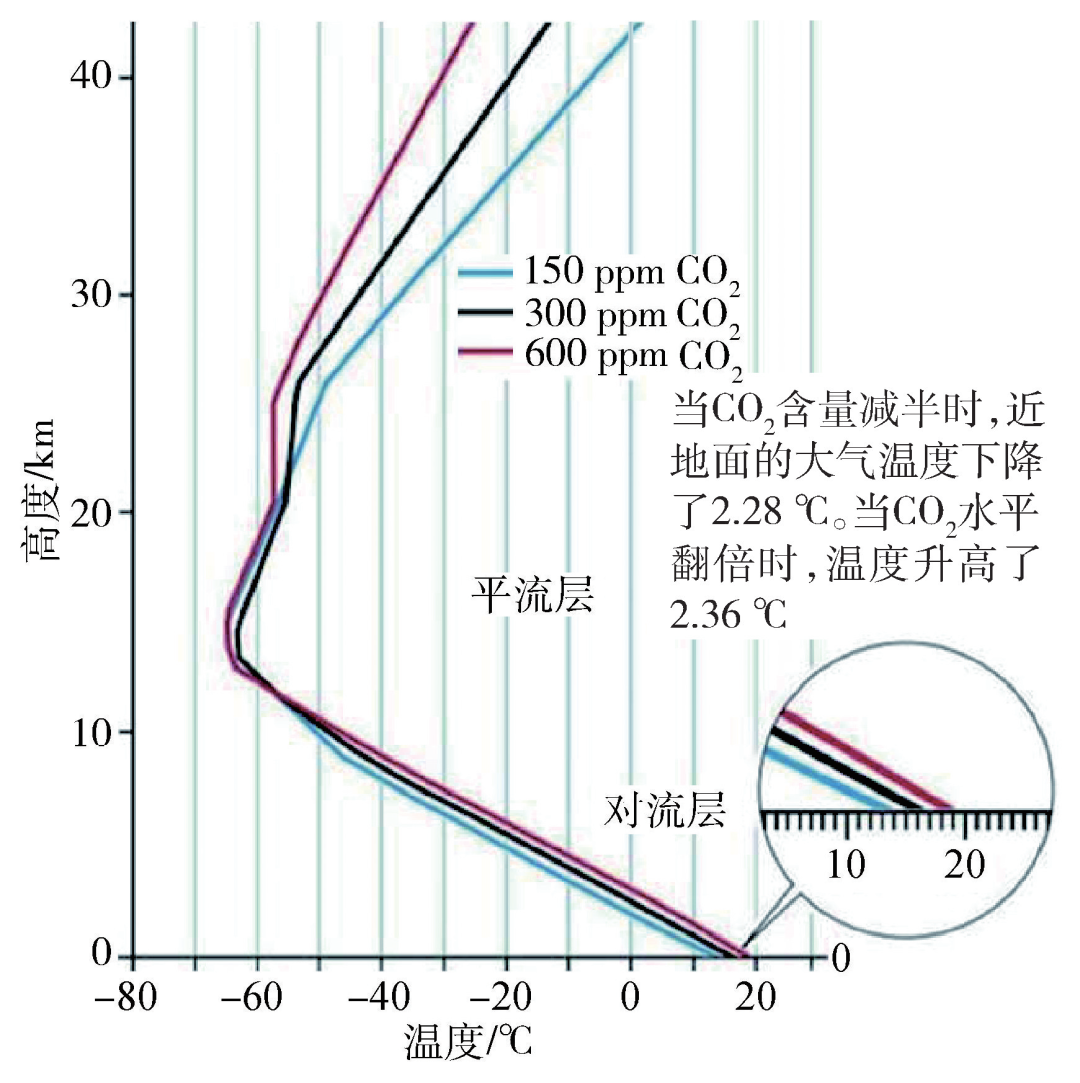
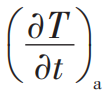 。在满足对流层质量守恒条件和地表热量平衡条件下,可以得到垂直温度廓线。
。在满足对流层质量守恒条件和地表热量平衡条件下,可以得到垂直温度廓线。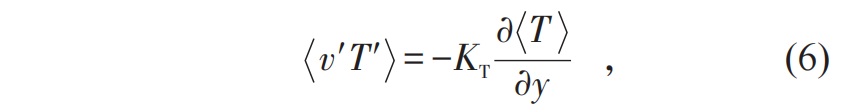
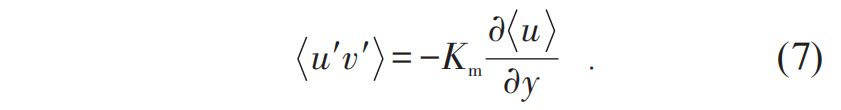
 表示。
表示。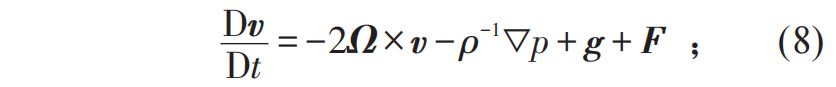
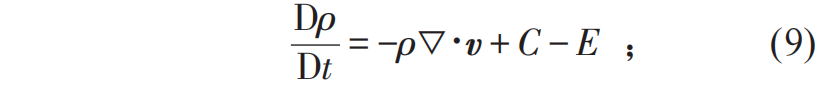

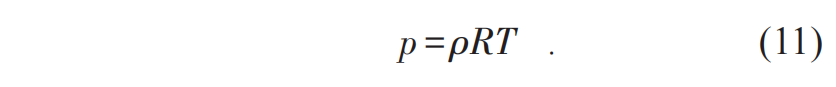
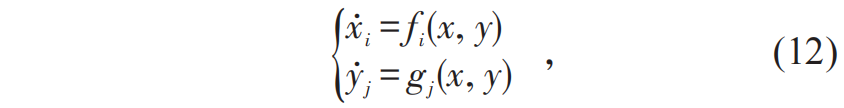
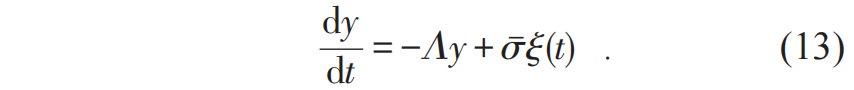
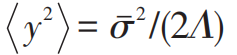 ,即涨落耗散关系。这意味着我们可以通过天气的噪声强度计算出宏观气候的涨落。
,即涨落耗散关系。这意味着我们可以通过天气的噪声强度计算出宏观气候的涨落。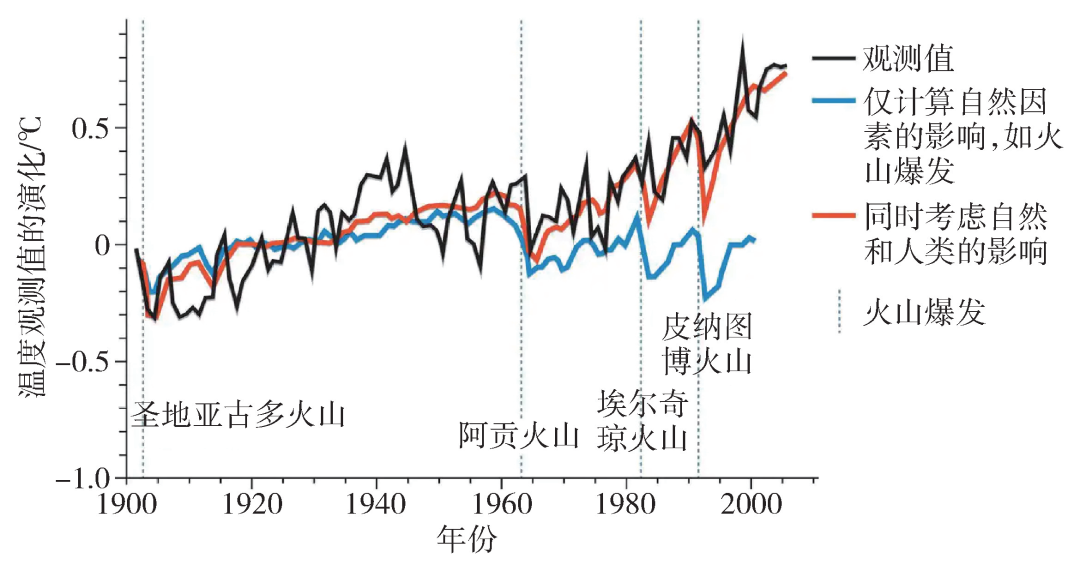
图4 哈塞尔曼开发出了可以用来识别气候变化中人类活动的指纹[24]
3. 无序系统
3. 无序系统
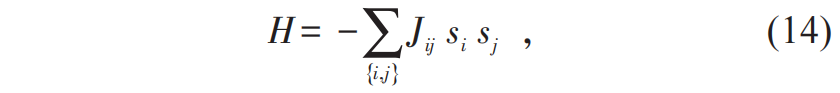

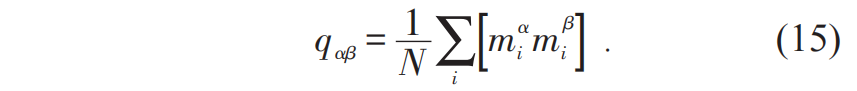
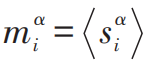 表示第α个复本中第i 个自旋的局域磁化强度。如果α=β,(15)式就给出了Edwards—Anderson序参量qEA[23]。
表示第α个复本中第i 个自旋的局域磁化强度。如果α=β,(15)式就给出了Edwards—Anderson序参量qEA[23]。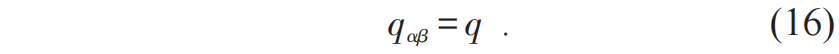
4. 结语与展望
4. 结语与展望
参考文献
(参考文献可上下滑动查看)
复杂科学最新论文
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅:

推荐阅读
-
Physics Reports重磅综述:统计物理和复杂系统理论在地球系统中的探索 -
重整化群:从微观到宏观,不同尺度的现象如何联系起来? -
网络科学前沿:既能造成极端天气,又能引发雾霾的“行星波” -
《张江·复杂科学前沿27讲》完整上线! -
成为集智VIP,解锁全站课程/读书会 -
加入集智,一起复杂!
点击“阅读原文”,查看论文原文










