导语


神经细胞网络在面对类似渗流的扰动时，会做出积极响应以缓解系统功能退化。近日，Nature Communications发表的一项研究提出了一个复杂网络中“扰动-响应”过程的数学理论框架，解释了局部守恒如何维持整个系统的全局连通性。结果表明，拥有稳态响应机制的结构更具韧性。


研究领域：生物网络，渗流效应

胡一冰 | 作者

邓一雪 | 编辑



论文标题：

Percolation in networks with local homeostatic plasticity

论文地址：
https://www.nature.com/articles/s41467-021-27736-0




1. 共识：优化边权以缓解渗流效应




复杂网络最吸引人的特征之一是它能承受扰动和攻击。当网络的边具有相同性质时，可以借助渗流理论的数学框架来研究系统韧性。在渗流过程中边以一定的概率被删除，通过跟踪最大连通片（the largest connected component, LCC）的规模和这个概率的关系来研究网络的连通性。最大连通片的大小表明网络在受到扰动后的连接比例，在交通或者是通信网络中可象征系统效率。研究渗流有助于理解网络结构对其韧性的影响，已有大量的研究专注于最大连通片规模的一阶、二阶相变。
 
优化边权的分配来获得更高的网络韧性是个老问题：在流行病学中这被称为“有针对性的免疫”，在电气工程领域设计高效电网，城市规划提升路网交通流量时均有运用。除此之外，一些生物复杂系统也会通过局部调节边权重来为网络整体效能带来积极影响。大脑网络和食物网络都被认为是通过一种自我调节机制来实现边权优化的，而这种机制是在受到扰动时才会触发。在这样的系统中，类似于“过滤”的过程伴随着主动响应以缓解由于删除网络边后带来的损失。例如神经元可以在扰动情况下，通过调整其突触强度以保障整体的神经活动。
 



2. 模型：稳态响应机制提升韧性




这篇文章给出了复杂网络中扰动响应过程的数学理论推导，该理论解释了如何保持节点的总入（出）权值局部守恒，反映了系统的全局连通性。研究通过“过滤”阶段的若干次迭代来对自适应网络退化建模，然后根据“稳态可塑性”原则（homeostatic plasticity principle）更新剩余边的权值，即每个节点的所有权值总和守恒。这一原理是受神经元中总突触强度守恒的启发。研究表明，这个能调整边权的简单、局部自我调节机制类似于神经元中突触的缩放，可以显著扩大网络的连通规模、维持网络效能，即使会损失一部分连边。
 

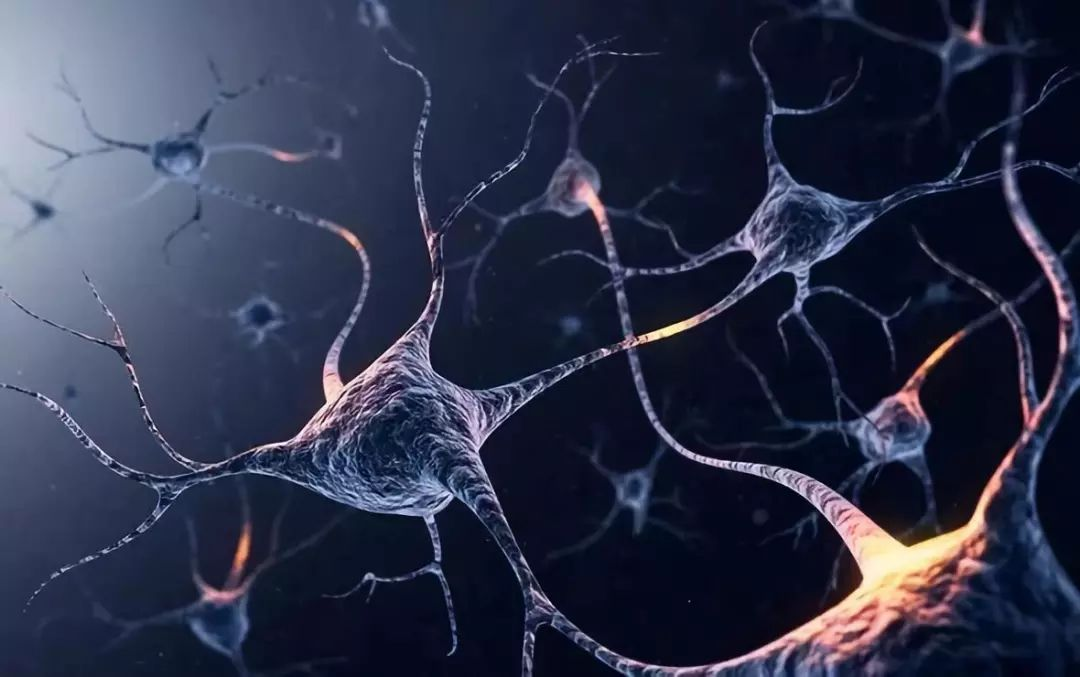
图1. 稳态可塑性：当神经元的兴奋性处于持续改变状态时，神经元会主动启动程序化的分子和细胞反应，对突触功能进行调节以对抗神经活性的持续性改变，从而使得突触传递和神经兴奋性维持在相对稳定的水平，维持正常的神经功能。

 
下面对模型基本参数进行简要说明—— 

  • 有向网络有任意度-权分布fk(x)：代表随机选择有向边权值在[x, x+dx]范围内且终止于度为k的节点的概率。
  • 联合概率fk(x)=lkwk(x)：lk代表网络的余度分布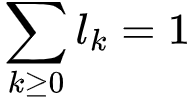，是随机选择一条边终止于度为k的节点的概率。wk(x)满足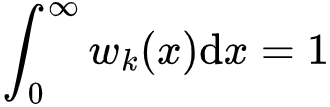，它是随机选择一条边终止于度为k的节点的概率密度函数，。
  • “扰动-响应”中作用于度-权分布的算子A：满足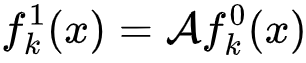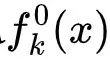，和 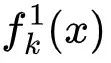分别表示边移除前、后的分布。
  • 解耦后算子A的卷积形式：Dk, y和Rk, y分别代表扰动和响应。


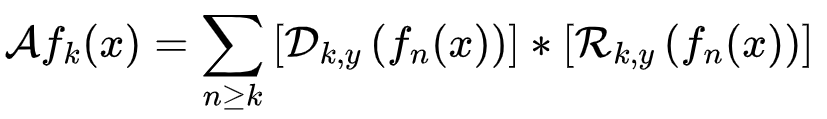 （式1）


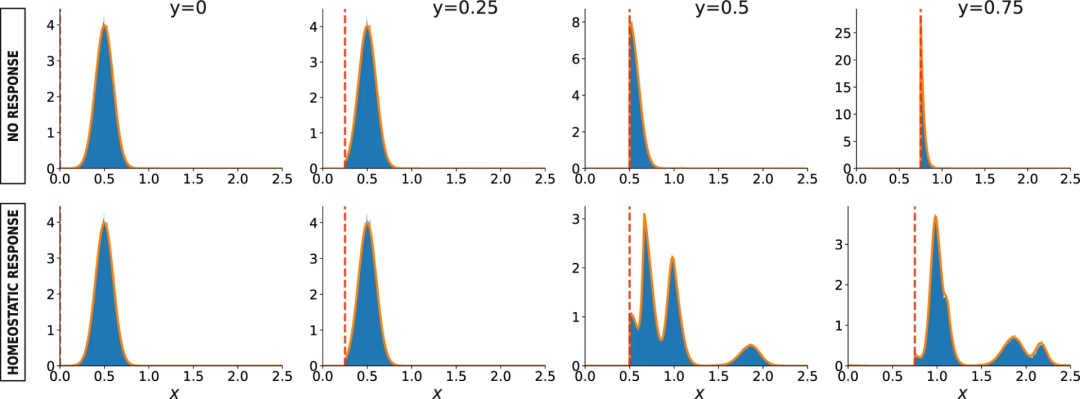
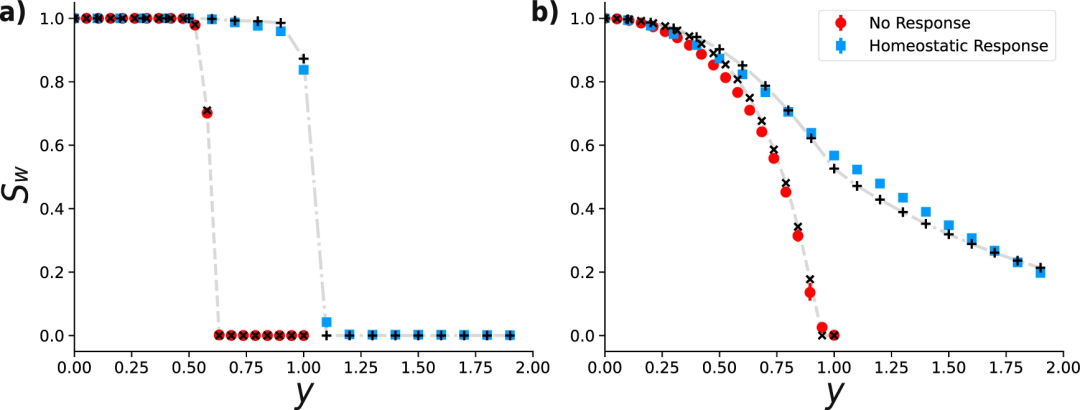
算子A为研究自适应退化现象提供了一个通用框架。现在来考虑“扰动-响应”机制的一个特定实例——前者由“过滤”表示，去除权重低于给定阈值y的所有边。后者则按照如下规则重新分配，m是满足边权重xi>y的边总数，是所有被移除边的权重之和。上面关于xi权重在分配的原则类似于神经元的稳态反应，是守恒的。


   （式2）


图2. 简单“过滤”与具有稳态响应的“过滤”
 
图2反映了上述的“扰动-响应”过程。子图a表示在扰动情况下，x2被移除后它的权重w2被平均分配到了另外两条边上，以保持网络的局部韧性。子图b上下两行反映了一般简单“过滤”与具有稳态响应的“过滤”的区别。网络下方的数轴表示随阈值y（红线）提升，部分边被移除后的边权分布（黑色）情况。可以看出，具有稳态响应机制的情况下，网络边权重总能保持在较为恒定的水平。
 
研究者利用式1来量化逐步“瓦解”过程中的网络的度-权分布，如图3所示，该研究在一个节点数N=5×104、边权呈正态分布的大型随机正则图上记录无响应（第一行）、有响应（第二行）情况下的总权分布w(x)演化情况。在每个图中显示了随机模拟的经验权重分布（蓝色）和模型预测结果（橙色），垂直虚线代表阈值。预测与随机模拟结果验证表明，该研究提出的模型能准确预测复杂模式。

图3. 稳态响应对边权分布的影响
 
从结构上看，整个网络的连通性由其中最大弱连通片（the largest weakly connected component）表征——巨片内部中的点相互连通，无关方向。研究者通过随不同阈值y下的度分布来量化对最大弱联通片规模Sw。结果表明，在存在稳态响应机制的情况下，最大弱联通片的“瓦解”被明显推迟。

图3分别展示了在随机图和经验脑网络中，由于内稳态响应机制，渗透效应均被显著延迟。彩色标记表示蒙特卡罗模拟结果，分别考虑了20个连续的无响应的渗透过程（红圈）和有稳态响应的渗透过程（蓝色方块），黑色标记表示模型中每个y值的相应估计值。

图4. 体内平衡反应延迟了巨片瓦解。
 
文章关于扰动对网络平均度和平均权重的量化进行了单独推导，在此不过多介绍。经验证，平均度和平均权重的分析预测与随机模拟之间具有良好的一致性。如图5所示，在四个不同结构的网络中红色标记为平均度，对应左侧坐标，蓝色标记为平均权重，对应右侧坐标。从图中可以看出，不同的网络结构极大地影响着变量之间的相关性。

图5. 扰动-响应过程中的平均度和平均权重。




3. 总结：稳态可塑性应用仍待拓展




渗流是一种通过使边或节点失效而降低网络连通性的过程，如疾病传播网络、交通网络等都具有渗流相变的特点。一些生物系统，如神经细胞网络，会对类似渗流的扰动做出积极响应，使得网络结构在退化时仍能保持其功能。
 
该研究结合稳态可塑性原理，自然地将经典渗流框架扩展到一个更复杂的维度。可以表明，与一般无响应的情况相比，稳态响应机制可以显著提高整个网络的效能。该文章为研究复杂网络中局部稳态可塑性规则及其对全局功能性影响之间的联系提供了一个数学框架，该理论框架揭示了局部缩放策略在生物网络中的作用，研究者们也表示希望此类设计能同样让基础设施网络更具韧性。
 

复杂科学最新论文


集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：



推荐阅读



点击“阅读原文”，追踪复杂科学顶刊论文