复杂系统的数据驱动建模：储备池计算教程

导语

对天气、湍流和股票市场等混沌系统，即使初始条件下有微小的不确定性，也会导致误差指数增长，从而限制了对此类系统的任何预测。虽然当前技术倾向于使用噪声和部分的测量信息来约束物理模型，但控制这些系统的方程通常是未知的。因此，使用机器学习等数据驱动方法来预测此类系统非常重要。储备池计算（Reservoir Computing）是一种简化的循环神经网络结构，在预测复杂系统的动力学方面已经显示出优越的性能。本文以洛伦兹吸引子为例，简要介绍了储备池计算在训练、预测和优化方面所需的代码，并讨论了优化以找到正确参数的重要性。

研究领域：混沌系统，洛伦兹吸引子，储备池计算，循环神经网络

Jason Platt | 作者

刘志航 | 译者

梁金 | 审校

邓一雪 | 编辑

确定性混沌这个几乎自相矛盾的概念描述的是这样的系统，它们对初始条件十分敏感以至于无法进行长期预测。因此，尽管动力学方程没有随机性，但即使是计算中最轻微的误差，例如计算机的数值精度误差，也会导致未来的预测谬以千里。

混沌系统的应用范围包括天气预报、流体中的湍流、等离子体动力学、化学反应、群体动力学、天体运动和股票市场等等。虽然当前技术倾向于使用充满噪声和部分的测量信息来约束物理模型（如卡尔曼滤波），但通常控制这些系统的方程是未知的。因此，能够使用机器学习 (ML) 等数据驱动方法来预测此类系统非常重要。

1. 洛伦兹“蝴蝶”吸引子

爱德华·洛伦兹（Edward Lorenz）在1963年开创了理解和洞察混沌动力学的新时代。洛伦兹对地球低层大气的对流进行简化，将确定性的、非周期性的行为以及“蝴蝶效应”（蝴蝶扇动翅膀就能改变天气）概念大众化。他的经典例子被称为“洛伦兹吸引子”（Lorenz Attractor）。该系统是三维的（3D），涉及从下方均匀加热并在上方冷却的稀薄流体的特性。下图绘制的是与对流速率和垂直温度变化相关的两个变量。洛伦兹吸引子是动力系统预测中的一个标准问题。

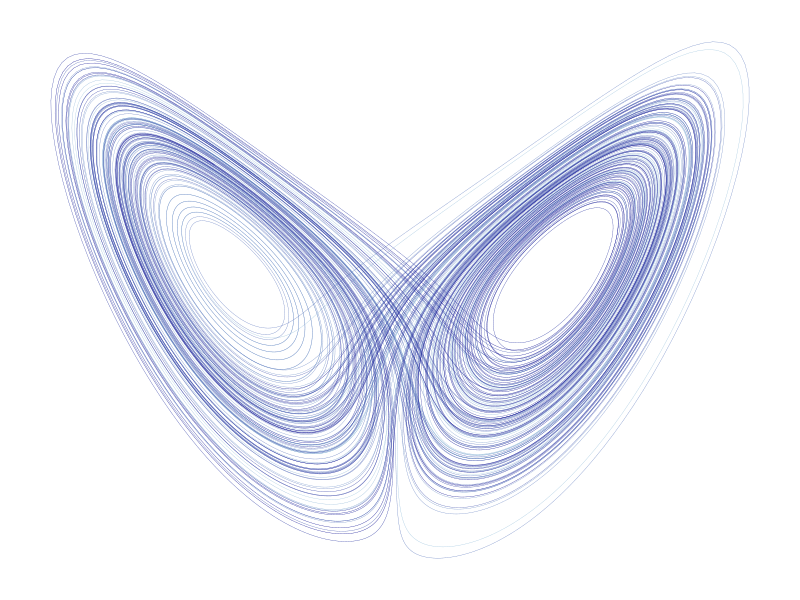
图1. 这里的几何对象被称为具有分形维数的“奇异吸引子”。准确地说，吸引子的维数是 2.06。| 图片来自作者

此处的三维数据 u(t) 来自一组常微分方程，一个动力系统。在此，我们深入谈一谈动力系统理论，“蝴蝶效应”可以由一组称为李亚普诺夫指数（Lyapunov Exponents，LE）的量来描述。李亚普诺夫指数是描述动力系统中扰动平均增长率的基本特征。

李普诺夫指数描述了最初相隔一段距离 δx₀=|x₁-x₂| 的两点 x₁ 和 x₂ 相对于彼此如何在时间上演化。更具体地说：

其中λ₁是最大的李亚普诺夫指数。因此，如果λ₁为正数，随着时间推移，最初仅相差很小的两个初始条件将在线性化体系中以指数级的速度快速偏离彼此，这就是混沌的定义和预测困难的原因。

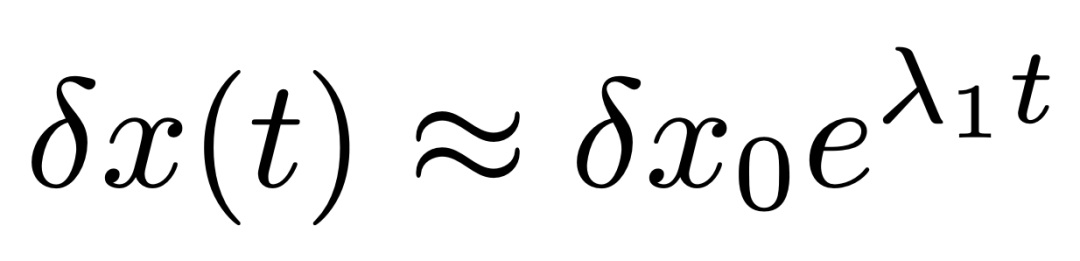
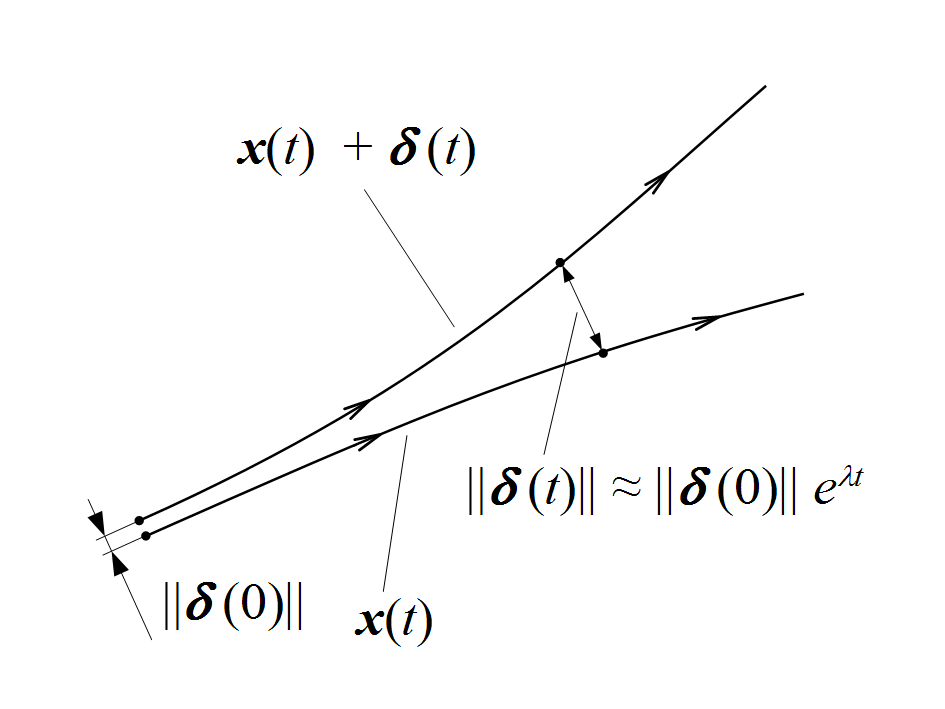
图2. 由正李亚普诺夫指数引起的扰动增长。| 图片来源：Yapparina 制作

李亚普诺夫指数可以直接与吸引子的维度和几何形状相关，吸引子是变量空间（称为相空间）中数据驻留的几何对象。λ₁ 也是误差指数增长的以时间的逆为单位的常数，因此李亚普诺夫时间 λ₁*t 给出了一个无量纲时间，可用于判断预测的质量。

2. 储备池计算

在机器学习中，有许多预测复杂系统的方法，然而最近有一种方法在性能、理解和训练的简单性以及基础动力学的再现方面脱颖而出，这就是储备池计算（Reservoir Computing）。储备池计算是循环神经网络（RNN）的一种简化形式。循环神经网络是一种具有自激励反馈连接的网络，其内部状态显式地依赖于先前的内部或“隐藏”状态和外部驱动信号。因此，数据有一个自然的排序，比如时序，这明确地允许将循环神经网络作为一个动力系统来处理。相比之下，其他形式的人工神经网络，如多层感知器不对数据进行排序，因此它们的自然数学描述是一个函数。

储备池计算的优点是避免了直接训练储备池本身的权重，它们是根据控制连接图属性的少量参数进行设置，这些整体参数是储备池计算方法的优势所在。设置这些参数可以看作是指定类似于气体的整体温度或压强，不需要跟踪单独每个粒子的位置和速度，大大降低了问题的复杂性。因此，训练仅限于在输出端解决线性回归问题，从而大大减少了训练时间。

图3. 储备池计算中的信息流。输入u(t) 通过输入层将信号投射到高维储备池中，使我们能够用线性读出层来逼近非线性动力学。然后，读出层预测 u(t+1)。接着将 u(t+1) 反馈到输入层，得到我们的预测。| 图片由作者提供

3. 储备池计算的结构

储备池计算的结构包括一个固定的（未经训练的）高维“储备池”和一个单一的训练输出层。储备池的固定性质减少了训练参数空间的大小，只需设置少数几个控制全局属性的参数，然后解决线性回归问题。这种对可搜索参数空间大小的减少，使人们能够轻松地绕过由于使用反向传播方法产生的梯度爆炸/梯度消失问题，并将循环神经网络的训练时间加快几个数量级。

表1：控制储备池整体性质的参数以及循环神经网络方程的更新

储备池计算由三层组成：输入层 Win，即储备池本身，以及输出层 Wout。储备池由N个节点组成，这些节点一般用简单的非线性元素（如 tanh 激活函数）进行作用。网络中的节点通过一个 N×N 邻接矩阵 A 连接，A 是随机选择的，其连接密度为 ρ_A，非零元素在 [-1, 1] 之间均匀选择，重新标度使得 A 的最大特征值表示谱半径（ρ_SR）。

通过以下代码我们可以尝试在 Julia 中初始化储备池计算，它被实现为一个对象，表1中的输入参数作为初始化参数。函数“get_connection_matrix”产生 N×N 的储备池，并标度最大特征值。

using Random
using SparseArrays
using Arpack

struct rc
“””Structure holding the reservoir computer

Args:
D::Int : Input system Dimension
N::Int : Reservoir Dimension
SR::Float : Spectral Radius
ρA::Float : Density of A
α::Float : Leak Rate
σ::Float : Input Strength
random_state::Int : Random seed
σb::Float : Bias
β::Float : Tikhonov regularization
“””
D::Int # Input System Dimension
N::Int # Reservoir Dimension
ρSR::Float64 # Spectral Radius of A
ρA::Float64 # Density of A
α::Float64 # Leak Rate
σ::Float64 # Input Strength
σb::Float64 # Input Bias
β::Float64 # Tikhonov Regularization
A::SparseMatrixCSC{Float64, Int64} # Adjacency Matrix
Win::Array{Float64,2} # Input Matrix
Wout::Array{Float64,2} # Output Matrix
rng::MersenneTwister # Random Number Generator

# Constructor Function
function rc(D, N, ρSR , ρA, α, σ, σb, β; random_state=111111)
rng = MersenneTwister(random_state)
A, Win, Wout = initialize_weights(D, N, ρSR, ρA, σ, rng)
new(D, N, ρSR , ρA, α, σ, σb, β, A, Win, Wout, rng)
end
end

function initialize_weights(D, N, SR, ρA, σ, rng)
A = get_connection_matrix(N, ρA, ρSR, rng)
Win = rand(rng, Uniform(-σ, σ), N, D)
Wout = Array{Float64}(undef, (D, N))
return A, Win, Wout
end

function get_connection_matrix(N, ρA, ρSR, rng)
# Define that numbers selected between [-1, 1]
rf(rng, N) = rand(rng, Uniform(-1.0, 1.0), N)

# NxN sparse random matrix
A = sprand(rng, N, N, ρA, rf)

# calculate eigenvalues and rescale
eig, _ = eigs(A, nev=1)
maxeig = abs(eig[1])
A = A.*(ρSR/maxeig)
return A
end

注：储备池计算采用表1中所示的参数。我们看到邻接矩阵A被实现为稀疏矩阵，因为已经证明，连接度非常低的储备池实际上预测效果最好（ρ_A~0.02）。此外，稀疏矩阵的矢量乘法也非常高效。然后，A 被其最大特征值重新标度。Win 在 [-σ, σ] 之间随机产生。Wout 的内存在初始化中被分配，但储备池计算还没有被训练。

输入层 Win 是一个 N×D 维矩阵，将输入信号 u(t) 从D维映射到N维储备池空间。Win的元素是在[-σ, σ]之间均匀选择。

4. 训练储备池计算

调用循环神经网络/储备池的隐藏状态 r(t)。更新规则是

在这里我们看到，下一个储备池隐藏状态 r(t+1) 取决于前一个状态 r(t) 和输入数据 u(t)。α 是“泄漏率”（leak rate），决定在下一个状态中有多少来自前一个状态的直接混合。节点上的非线性元素由 tanh 函数给出，在这种情况下效果很好，因为它以0为中心。

训练包括用数据 u(t) 驱动储备池计算，并生成一系列与数据相匹配的储备池状态 r(t)。然后我们通过优化损失来确定 u(t) 和 r(t) 之间的线性映射 Wout

其中r是包含r(t)的矩阵，u是包含训练数据集中所有t的u(t)的矩阵，β是 Tikhonov-Miller 正则化超参数。这也被称为“岭回归”（ridge regression）。其解是

其中I是N×N的单位矩阵。因此，训练是一个简单的矩阵乘法问题。我们可以看看这在代码中是怎样的：

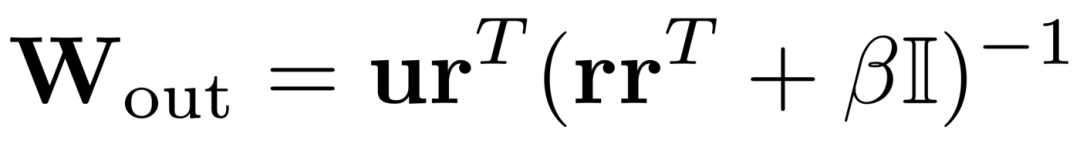
function train_RC(rc::rc, u; spinup = 100, readout = false)
“””Train the rc
This function sets the matrix rc.Wout
u ∈ D×T
r ∈ N×T
Args:
rc : reservoir struct
u : Array of data of shape D×Time
spinup : Amount of data to use for spinup
Returns:
if readout=true: Wout*r, the readout of the rc training data
else: return the last state of r, can be used to predict
forward from the training data
“””
r = generate(rc, u)
compute_Wout(rc, r[:, 1+spinup:end], u[:, 1+spinup:end])
if readout == true return rc.Wout*r end
return r[:, end]
end

function driven_rc!(rtp1, rc::rc, rt, ut)
“””Drive the rc with data

Args:
rtp1 : r(t+1)
rc : reservoir computer
rt : r(t)
ut : u(t)
“””
rtp1[:] .= rc.α.*tanh.(rc.A*rt .+ rc.Win*ut .+ rc.σb).+(1 .- rc.α).*rt
end

function generate(rc::rc, u)
T = size(u)[2]
r = Array{Float64}(undef, (rc.N, T))
r[:, 1] = zeros(rc.N)
for t in 2:T
driven_esn!(r[:, t], rc, r[:, t-1], u[:, t-1])
end
return r
end

function compute_Wout(rc::rc, r, u)
rc.Wout[:, :] .= (Symmetric(r*r’+esn.β*I)(r*u’))’
end

注：训练储备池计算需要输入一个数据序列 u(t)。我们生成对应于输入u(t)的隐藏状态r(t)，从那里可以计算出输出矩阵。

储备池计算还需要一些步骤来与数据同步。我们把这称为“旋转”（spinning up）。

5. 预测

现在进行预测。我们用 Wout*r(t) 代替 u(t)，把被动的储备池计算变成一个自主（只取决于r(t)的）系统

这为我们提供了“预测机器”，只要我们想，就可以简单地在时间上向前迭代。代码如下，注意 “auto_rc”函数与“driven_rc”函数相同，但 u->Wout*r。

function forecast_RC(rc::rc, nsteps; uspin=nothing, r0 = nothing)
“””Forecast nsteps forward in time from the end of uspin or from rc state r0
Make sure to train the RC before forecasting. Requires either uspin or r0.
If both are provided will use uspin to set r0.
“””
if !isnothing(uspin)
rspin = generate(rc, uspin)
r0 = rspin[:, end]
end
@assert !isnothing(r0)

# Initialize array of hidden states and set r(0)=r0
rfc = Array{Float64}(undef, (rc.N, nsteps))
rfc[:, 1] = r0

# Now iterate the autonomous RC nsteps times for the forecast
for t in 1:nsteps-1
auto_esn!(rfc[:, t+1], rc, rfc[:, t])
end
return esn.Wout*rfc
end

function auto_rc!(rtp1, rc::rc, rt)
“””Autonomous RC update rule”””
rtp1[:] .= rc.α.*tanh.(rc.A*rt .+ rc.Win*rc.Wout*rt .+ rc.σb).+(1 .- rc.α).*rt
end

注：预测可以从一小片数据 uspin 或一个储备池状态 r(0) 开始。然后函数会预测 n 步之后的状态。

6. 洛伦兹吸引子示例

这里我们从洛伦兹系统中创建一些训练和测试数据。BasicReservoirComputing 是具有上述储备池计算代码的模块。系统的大小为D=3，而储备池有N=200个节点。参数如下 σ=0.084；α=0.6；SR=0.8；ρA=0.02；β=8.5e-8；σb=1.6，这是通过下一节描述的优化程序找到的。我没有定义 make_lor63 和 plot_prediction，但它们可以在 github repo 中找到。整个过程只需要几秒钟。

using BasicReservoirComputing
using Plots

function L63_ex()
# make the training and testing data (not defined here)
utrain, utest = make_lor63(train_time = 100, test_time = 20, n_test = 100)

#define the RC
D=3; N=200; σ=0.084; α=0.6; SR=0.8; ρA=0.02; β=8.5e-8; σb=1.6; Δt=0.01
reservoir = rc(D, N, ρA, Δt, SR, α, σ, σb, β))

# Training
nspin = 100
train_RC(reservoir, utrain, spinup=nspin)

# Forecast and compare to truth
utrue = utest[:, nspin:end]
nsteps = size(utrue)[2]
upred = forecast_RC(rc, nsteps, uspin = utest[:, 1:nspin])

# now plot results (not defined here)
t = collect(0:nsteps-1)*Δt
p = plot_prediction(t, upred, utrue)
display(p)
end
L63_ex()

在下面的例子中，我们看到了储备池计算的关键优势之一。不仅预测结果非常好，这里达到了~9个李亚普诺夫时间，而且当预测最终发散时（由于“蝴蝶效应”必须如此），储备池计算保持在吸引子上，并给出“物理预测”，预测具有与实际数据相同的统计特征。

我们可以计算出储备池计算的D个最大的李亚普诺夫指数，并与输入数据的李亚普诺夫指数进行比较。当两者匹配时，我们就会得到这样的特征，即未来的预测与数据“气候学上相似”。这意味着预测具有与输入数据相同的统计属性（平均值、标准差、相关性、误差增长……）。

复现正确的误差增长统计（李亚普诺夫指数）的属性不仅对预测的稳定性很重要，而且对将循环神经网络纳入当前最先进的预测方法，如集成卡尔曼滤波或其他形式的数据同化也很重要。这些方法使用贝叶斯推断，将稀疏和嘈杂的观测数据纳入系统的模型（数据驱动或物理）。推理需要模型的扰动集合再现物理上真实的扰动预测，因此这一特性非常重要。

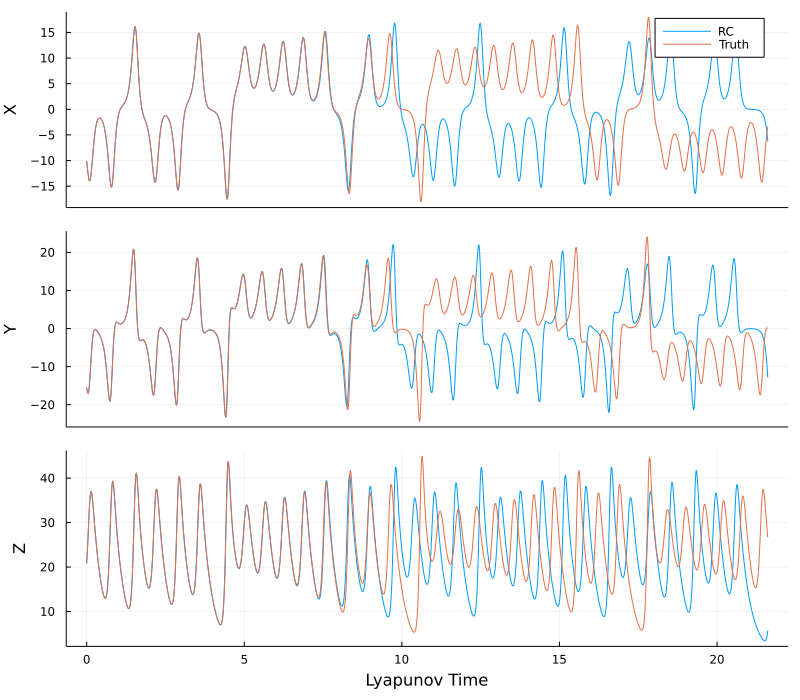
图4. 从t=0开始对X、Y和Z进行预测。注意良好的短期预测以及长期统计的再现。图片由作者提供。

7. 测试储备池计算

一个常见的时间序列预测的机器学习基准是单步预测的均方误差。事实上，这正是我们训练Wout 以获得 u(t)→r(t)→u(t+1) 的线性映射方法。然而，作为一种测试方法，单步预测并不是一个合适的指标；它过分强调了数据中的高频模式，而牺牲了储备池计算预测的长期稳定性。

我们预测时间的标准指标是有效预测时间 (valid prediction time，VPT)。VPT 是预测准确度超过给定阈值的时间 t。例如，

其中D是系统维度，σ是时间序列的长期标准差，ε是一个任意的阈值，uᶠ是储备池计算预测。

我们可以通过下面的直方图看到不同初始条件下预测的统计系综的重要性。这个系综是通过训练一个储备池计算，然后在洛伦兹吸引子的不同点上对大量的初始条件进行测试而产生的。预测时间的变化部分是由于动力系统运动的不稳定性的变化造成。洛伦兹吸引子在中间有一个不稳定的鞍点，在那里，极难预测状态会在“蝴蝶”的哪一边翅膀上结束，而两个翅膀的中心则相当稳定。

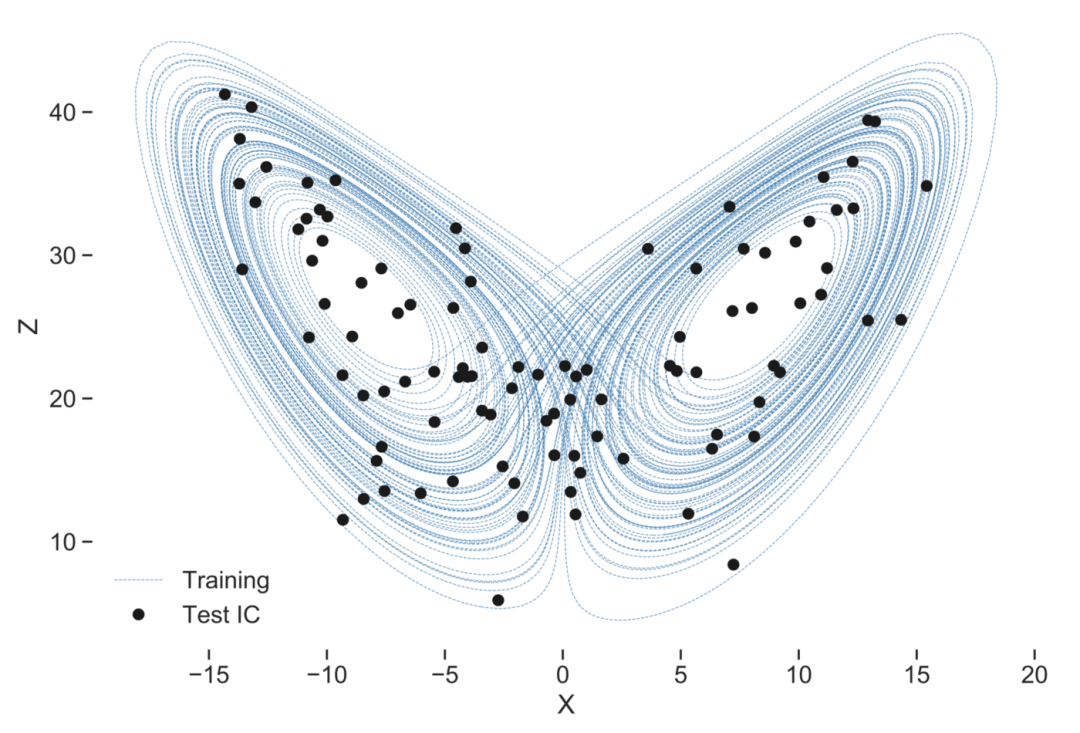
图5. 测试储备池计算的初始条件。这些预测的有效预测时间（VPT）显示在下面的直方图中。从吸引子的中心开始预测未来的行为要比从叶片开始预测难得多。图片由作者提供。

图6. 直方图显示上述100个初始条件下的预测时间分布。图片由作者提供。

8. 如何找到正确的参数

为储备池计算找到正确的参数是使用该技术的主要挑战之一。正如我们在下面看到的，预测能力对我们选择的参数值相当敏感，使得这是一个有点困难的多维非线性优化问题。值得庆幸的是，有许多算法专门处理此类问题，例如 CMAES，但任何全局优化算法都可以。

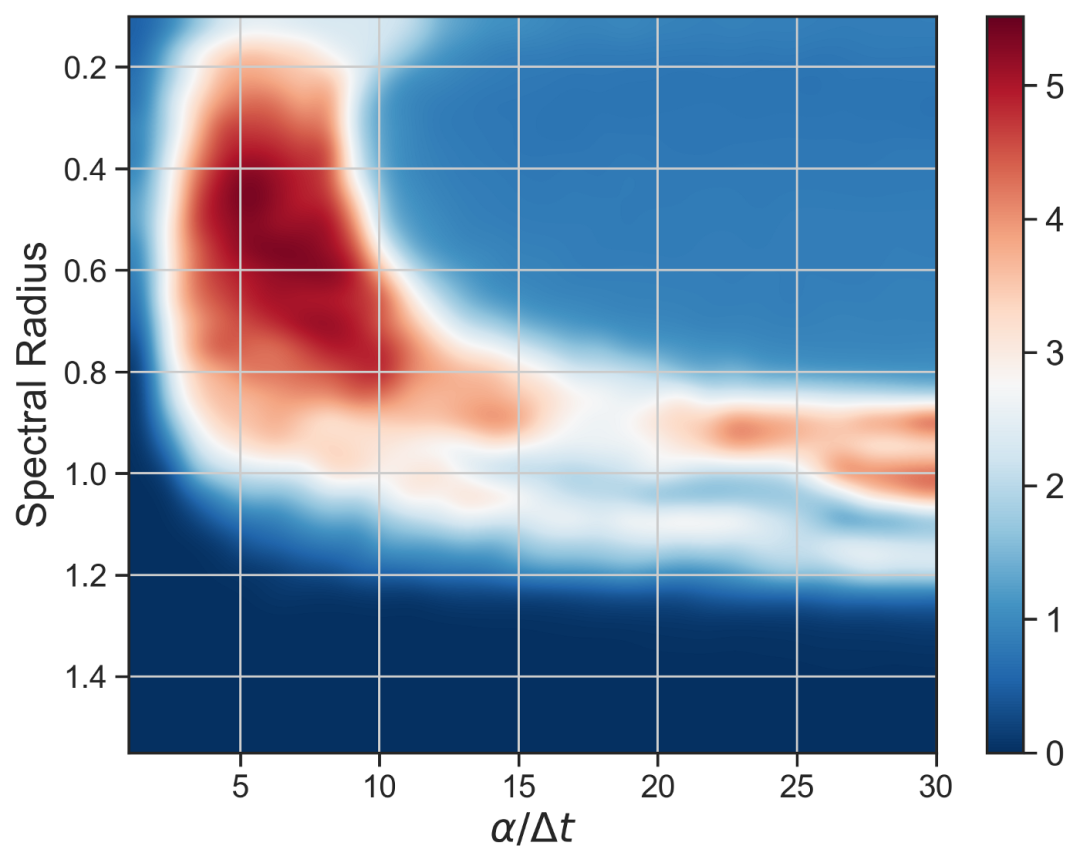
图7. 预测对储备池计算参数变化的敏感度。红色表示平均VPT高的区域，蓝色表示VPT低的区域。在整个参数空间中进行搜索是一个不简单的问题。图片由作者提供。

我将采用一个三步优化方法。该程序是

1、固定参数

2、通过线性回归训练Wout

3、通过一系列长期预测评估损失函数

我用来评估数据拟合的损失函数是：

其中 M 是用于比较的预测数目。uᶠ是预测值，u是数据。指数项是为了抵消预期误差在时间上的指数式增长。

增加 M 可以平滑损失函数，并能够更好地收敛到全局最小值。然而，妥协是必要的，因为增加 M 将大大增加计算复杂性。我们凭经验发现，对于简单模型而言，使用 15~20 个左右的预测通常就足够了，只要这些预测是在统计上独立的点（彼此相距超过几个李亚普诺夫时间尺度）进行的。理想情况下，数据会很好地对输入系统吸引子进行采样，但实际上并非总是如此。

下面我们看到要最小化的目标函数和单次未来预测的损失函数的定义。该代码依赖于一个包含非优化参数和训练数据的对象f（此处未显示）。然后，我们使用全局优化程序来优化不同的参数。

function Loss(data, spinup_steps, rc::esn)
“””Loss function for an individual forecast”””
uspin = data[:, 1:spinup_steps]
utrue = data[:, spinup_steps:end]
Ttrue = size(utrue)[2]
upred = forecast_RC(rc, Ttrue; uspin=uspin)

err = upred.-utrue
weight = exp.(-(1:Ttrue)./Ttrue)
return norm(err.*weight’)
end

function obj(θ)
“””The objective function to minimize over the optimization

Args:
θ : Array of parameters

Returns:
objective value
“””
SR, α, logσ, σb, logβ = θ
D, _ = size(f.train_data)

# build the RC
rc = esn(D, f.N, SR, f.ρA, α, exp(logσ), σb, exp(logβ))

# Train the RC
train_RC(rc, f.train_data)

# Compute loss over n_valid forecasts
n_valid = length(f.valid_data_list)
loss = zeros(n_valid)
for i in 1:n_valid
loss[i] = Loss(f.valid_data_list[i], f.spinup_steps, rc)
end

# Objective is sum of loss functions
return sum(loss)
end

9. 总结

我们简要介绍了储备池计算，以及训练、预测和优化储备池计算以预测复杂系统所需的代码。讨论了优化以找到正确参数的重要性，以及储备池计算复现输入数据的长期统计数据的能力。虽然我们仅以洛伦兹系统为例，但储备池计算有许多更复杂的应用。

可以在以下位置找到代码和示例：

https://github.com/japlatt/BasicReservoirComputing

关于储备池计算背后理论的更多信息，以及对设计选择的更深入的讨论，可以在以下论文中找到。如果你觉得这些信息有用，请引用它们。

1. Jason A. Platt et al. “Robust forecasting using predictive generalized synchronization in reservoir computing”. In: Chaos 31 (2021), p. 123118. URL: https://doi.org/10.1063/5.0066013

2. Platt, J. A., Penny, S. G., Smith, T. A., Chen, T.-C., & Abarbanel, H. D. I. (2022). A Systematic Exploration of Reservoir Computing for Forecasting Complex Spatiotemporal Dynamics. arXiv http://arxiv.org/abs/2201.08910

关于将循环神经网络整合到数据同化算法中，以处理稀疏/噪声/不完整数据的信息：

Penny, S. G., Smith, T. A., Chen, T.-C., Platt, J. A., Lin, H.-Y., Goodliff, M., & Abarbanel, H. D. I. (2021). Integrating Recurrent Neural Networks with Data Assimilation for Scalable Data-Driven State Estimation. arXiv [cs.LG]. Opgehaal van http://arxiv.org/abs/2109.12269

这篇文章的最初灵感来自于 Lu 等人2018年的工作：

Zhixin Lu, Brian R. Hunt, and Edward Ott. “Attractor reconstruction by machine learning”. In: Chaos: An Interdisciplinary Journal of Nonlinear Science 28.6 (2018), p. 061104. DOI: 10.1063/1.5039508

本文翻译自：Towards Data Science

原文题目：

Data Driven Modeling of Complex Systems: A Reservoir Computing Tutorial

原文链接：

https://towardsdatascience.com/data-driven-modeling-of-complex-systems-8a96dc92abf9

复杂科学最新论文

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：

推荐阅读

点击“阅读原文”，追踪复杂科学顶刊论文