代谢可塑性可增强生态系统对全球变暖的反应 | 复杂性科学顶刊精选7篇
集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。
扫描下方二维码，关注“集智斑图”服务号，即可订阅Complexity Express： 
Complexity Express 一周论文精选
目录：
1、代谢可塑性可增强生态系统对全球变暖的反应
2、并行机器学习在复杂网络动力学预测中的应用
3、湍流中物质环的统计几何学
4、基于知识提取的通信高效联邦学习
5、二分网络模型设计急性髓系白血病联合治疗方案
6、神经网络中的 Gell-Mann–Low 临界性
7、生成模型学习的神经编码框架
1. 代谢可塑性
可增强生态系统对全球变暖的反应
论文题目：Metabolic plasticity can amplify ecosystem responses to global warming 论文来源：Nature Communications 论文链接：https://www.nature.com/articles/s41467-022-29808-1
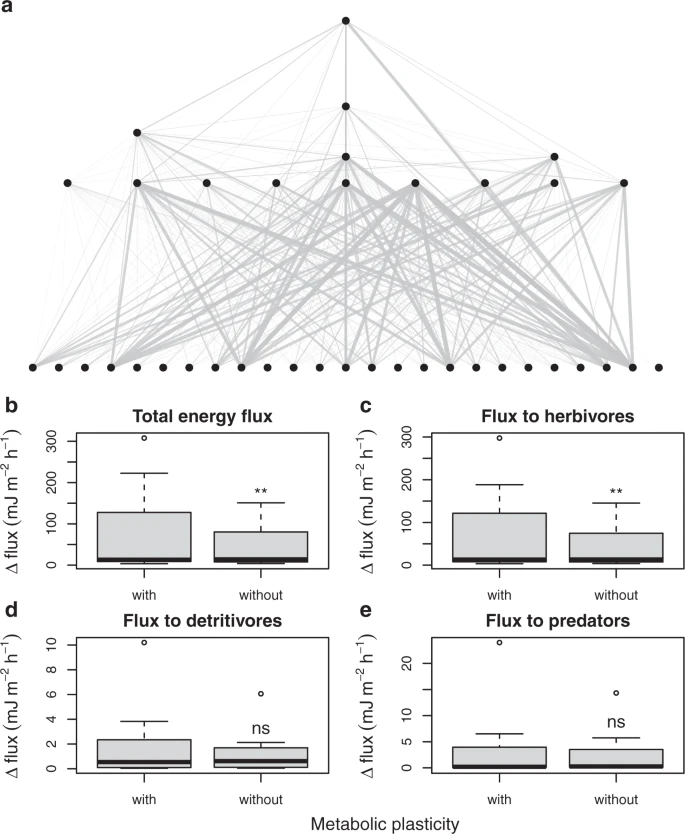
图：（a）在模拟+2 °C变暖后，通过研究系统中食物网模拟的能量通量变化的可视化。物种种群（节点）之间较粗的线（营养联系）表明，与没有代谢可塑性的模型相比，使用具有代谢可塑性的模型预测的能量通量增加更大。（b）使用来自我们 14 个研究地点的经验数据，具有代谢可塑性的模型预测，在 +2 °C 变暖后，通过网络的总能量通量比没有代谢可塑性的模型显着增加。这种增加是由（c）向草食动物的通量驱动的，而对（d）食腐生物或（e）捕食者的通量增加没有显著贡献。图中显示了Tukey箱线图和盒须图，粗黑线为中位数，界限为第1和第3个四分位数，外横线为四分位间距的1.5 倍，异常值为单个点。
2. 并行机器学习
在复杂网络动力学预测中的应用
论文题目：Parallel Machine Learning for Forecasting the Dynamics of Complex Networks
论文来源：Physical Review Letters
论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.164101
利用过往的时序数据预测大型复杂稀疏网络的动力学特征， 在广泛的应用背景下很重要 。在这里，我们提出一个机器学习方案，使用一个模拟相关网络拓扑结构的并行架构来完成这一任务。通过在一个混沌网络振荡器上的储备池计算案例，我们展示了该方法的实用性和可扩展性。我们考虑了两种情况的先验知识：(i) 网络链接是已知的；(ii) 网络链接是未知的，需要通过数据驱动的方法推断，以便于近似优化预测。
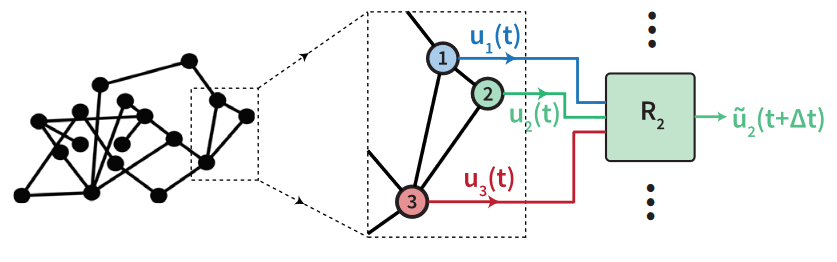
图：并行网络机器学习架构的示意图。这里我们展示了储备池2（R2），它接收来自其指定节点（节点2）的输入，加上与节点2相连的节点（即节点1和3）的输入。然后，R2被训练以预测其分配的节点（节点2）。这个过程对网络中的每个节点都是一样的，这样，储备池之间的连接就模仿了要预测的网络。
3. 湍流中物质环的统计几何学
论文题目：The statistical geometry of material loops in turbulence
论文来源：Nature Communications
论文链接：https://www.nature.com/articles/s41467-022-29422-1
随着时间的推移，混沌流（chaotic flow）倾向于将材料的元素折叠、扭动和褶皱成近似无限复杂的状态。一个基本的问题是，这个动荡的过程是否具有任何长期持续存在的可预测特征。回答这个问题可以深入了解发生在整个系统中的混合过程，从染料扩散到水中、浮游生物群落在海洋表面的扩散，到超新星热核爆炸中的爆炸传播。在这些过程中，材料的元素——呈现为被动、非扩散标记的曲线、曲面或体积，为我们提供了一个内在的几何学视角，以了解混沌流的复杂动力学。
在本文中，研究人员揭示了湍流环境中物质环的稳健统计性质。本文采取的方法结合了 Navier-Stokes 湍流的高精度直接数值模拟、随机模型以及动力系统方法，以揭示这些复杂物体可预测的普遍特征。研究人员在本文中表明，环的曲率统计性质在通过高曲率褶皱动态形成过程后变得稳定，导致了统计分布具有幂律尾部，且其指数由流动的有限时间 Lyapunov 指数的大偏差统计确定。这一预测适用于广泛混沌流中的平流物质线。为了补充这一动态图景，研究用精确的 Fokker-Planck 方法在可解析的 Kraichnan 模型中确认了理论。
图：最初的圆环（颜色对应于初始角度）在 27τη 内的湍流场平流，其中 τη 是 Kolmogorov 时间。 湍流的扭曲和折叠作用产生了复杂的环几何形状，而环的长度平均呈指数增长。 所示的循环是一个比较极端的情况。经过较长时间后，湍流较小区域中的环路会形成扩展且复杂的结构。插图为导致曲率峰值的材料折叠。
4. 基于知识提取的
通信高效联邦学习
论文题目：Communication-efficient federated learning via knowledge distillation
论文来源：Nature Communications
论文链接：https://www.nature.com/articles/s41467-022-29763-x
联邦学习是一种保护隐私的机器学习技术，用于从分散的数据中训练AI模型，在模型训练的每一次迭代中，联邦学习算法会利用收到的局部数据更新模型，而不是全局数据，从而实现对隐私数据的利用和保护。然而，如果模型更新包含大量的参数，那么模型的更新数据可能会非常大，而且模型训练也需要很多轮的通信。联邦学习中巨大的通信成本导致了客户端的开销过大和高环境负担。在这里，我们提出了一种名为FedKD的联邦学习方法，基于自适应互相知识提取和动态梯度压缩技术，既可以节省通信成本又能有效训练模型。在三个不同的需要隐私保护的场景上对FedKD进行了验证，结果表明，FedKD最多能降低94.89%的通信开销，取得了与集中式人工智能模型学习相媲美的结果。FedKD提供了在许多场景中高效部署隐私保护智能系统的潜力，例如智能医疗保健和个性化学习。
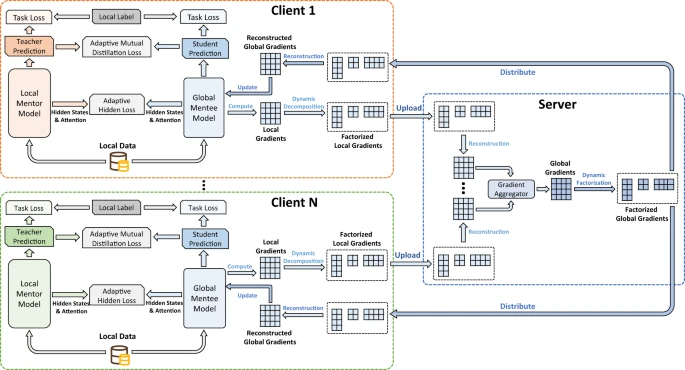
图：FedKD 框架，利用本地数据对 local mentor 模型和 global mentee 模型进行训练。两种模型都是从局部标记数据以及预测结果和隐藏结果中学习。本地梯度在上传到服务器之前进行分解，然后在服务器上重新构建以进行聚合。聚合的全局梯度进一步分解并分发给客户端以进行本地更新。
5. 二分网络模型
设计急性髓系白血病联合治疗方案
论文题目：Bipartite network models to design combination therapies in acute myeloid leukaemia
论文来源：Nature Communications
论文链接：https://www.nature.com/articles/s41467-022-29793-5
对癌症联合治疗的疗效和安全性优于单一靶点治疗。然而，确定有效的药物组合需要时间和资源。我们提出了一种通过对患者相关药物反应数据，特别是Beat AML数据集，使用二分网络建模来识别潜药物组合的方法。该方法利用细胞活力中位数作为药效测量指标，构建加权二分网络，建立药物-生物样品相互作用模型，并在两个投影网络中寻找节点簇。然后，利用聚类结果发现有效的多靶点药物组合，这也得到了更多来自GDSC和ALMANAC数据库的证据的支持。选择药物组合的效力和协同作用水平，在三种急性髓系白血病细胞系的体外单一治疗中得到证实。在这项研究中，我们介绍了一种数据挖掘方法，以通过组合疗法改善急性髓系白血病的治疗。
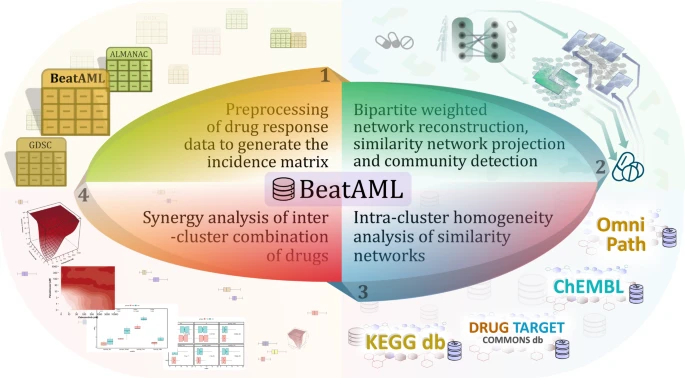
图：数据收集和预处理从Beat AML药物反应数据集开始，然后是关联矩阵提取、加权二分网络重建、网络投影和社区发现。使用ChEMBL、Omnipath、DrugTargetCommons和KEGG数据库，根据现有的基因表达谱、药物-靶点相互作用、蛋白质-蛋白质相互作用和生物路径，利用所有集群的药物和病人/细胞成员的相似性进行集群内同质性分析。 此外，额外的药物反应数据集GDSC和ALMANAC分别用于集群内同质性分析和集群间药物组合策略步骤，以检查所提出的工作流程是否独立于数据集。
6. 神经网络中的
Gell-Mann-Low临界性
论文题目：Gell-Mann–Low Criticality in Neural Networks
论文来源：Physical Review Letters
论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.168301
临界性与最佳计算能力有着深刻的联系。然而，到目前为止，由于缺乏大脑临界动力学的重整化理论，对这种形式的生物信息处理的理解仅限于平均场结果。这些方法忽略了临界系统的一个关键特征：跨越所有长度尺度的自由度之间存在相互作用，这是复杂的非线性计算所需要的。我们提出了一个典型的神经场理论的重整化理论，即随机的威尔逊-考恩模型（Wilson-Cowan model ）。我们计算了耦合流，它在不断增加的长度尺度上参数化相互作用。尽管与 Kardar-Parisi-Zhang 模型有相似之处，但该理论属于 Gell-Mann-Low 类型，是可重整化量子场论的典型形式。在这里，非线性耦合消失，流向高斯固定点，但对数缓慢，因此在大多数尺度上仍然有效。我们展示了这种临界的相互作用结构，以实现信息存储的最佳线性和计算所需的非线性之间的理想权衡。
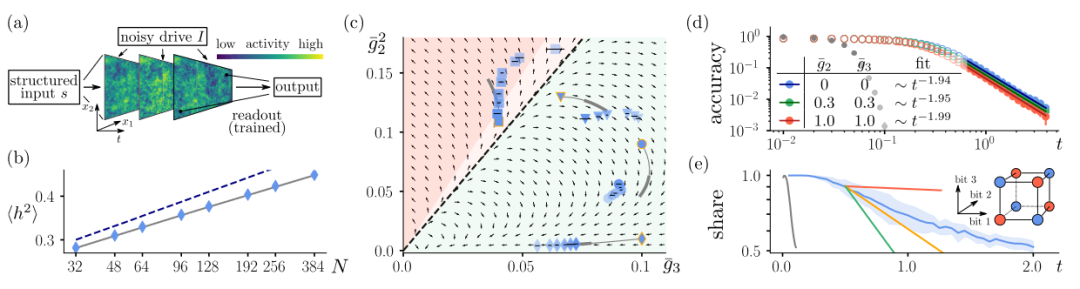
图：（a）一个线性读数被训练成从神经活动中提取所需的输入-输出映射。集体非线性相互作用是实现复杂映射的基础。因此，我们需要超越平均场方法，在逐渐增加的长度尺度上跟踪非线性相互作用。(b) 方差，蓝色钻石：模拟；深蓝色虚线：线性系统；灰色实线：重整化理论。（c）耦合流，过渡线（黑色虚线）将收敛区（绿色）和发散区（红色）分开。（d）记忆，对于不同强度的非线性，高斯输入随时间的重建精度（0：完全遗忘；1：完美重建）。（e）分类，正确分配给3位字符串的奇偶性份额（蓝色曲线）和重复训练的标准偏差（阴影区）。读出时最慢（红色）、中间（橙色）和最快（绿色）模式的衰减时间尺度。
7. 生成模型学习的神经编码框架
论文题目：The neural coding framework for learning generative models
论文来源：Nature Communications
论文链接：https://www.nature.com/articles/s41467-022-29632-7
神经生成模型可以用于从数据中学习复杂概率分布（complex probability distribution），采样并估计概率密度函数。受大脑预测处理理论（predictive processing theory）启发，我们提出一种神经生成模型的计算框架。根据该理论，大脑中某一层的神经元会对另一层传来的感官输入做出预测，并根据预测与观测信号的差别调整模型参数。类似地，在我们提出的生成模型中，人工神经元也会预测相邻神经元的行为，并根据预测的准确性调参。我们所提出框架下的神经生成模型在几个基准测试数据集和衡量标准下表现良好，可以媲美或远超其他功能相似的生成模型，如变分自编码器（variational auto-encoder）。
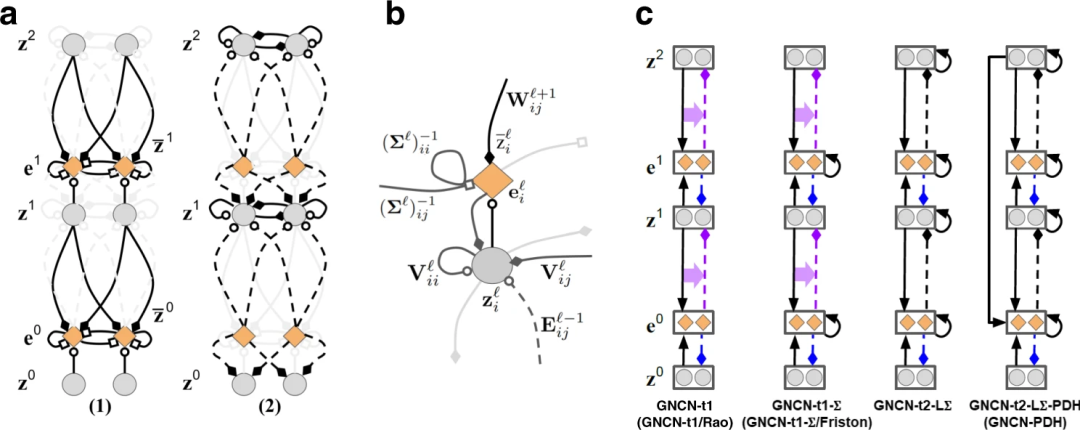
图：神经生成编码、计算和环路。（a）神经生成编码中两个重要计算步骤：（1）预测和侧向错误计算；（2）神经状态的误差-纠正。图中绘制了一个3层的简单网络，每层由2个状态神经元组成（灰色圆），在T步里迭代更新。其中两层神经元与误差神经元（橙色钻石形）连接，误差神经元计算在整个系统中传播的误差信息。底层z0接收感官输入（一张图片）。（b）神经生成编码中基本神经元计算单元，在l层里由一个状态神经元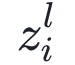
，一个误差神经元
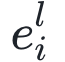组成。在这个环路中，一个状态神经元不仅接收误差神经元的信息（由
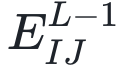传递），还接收一个自激发信号（由
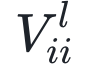传递）和侧向连接神经元传来的抑制信号（由
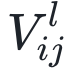传递）。误差神经元接收从侧向连接神经元传来的增益信号（由
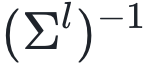传递）。（c） 该研究中采用的不同神经生成编码结构。黑色实箭头代表生成权重，黑色虚箭头代表误差权重，淡粉色虚箭头代表临时（虚拟）反向传播误差通路，这是一个生成权重的函数，即误差权重的转置（粉色水平实箭头代表哪个前向权重被用于制作反向通路权重）
2. 并行机器学习
在复杂网络动力学预测中的应用
论文题目：Parallel Machine Learning for Forecasting the Dynamics of Complex Networks 论文来源：Physical Review Letters 论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.164101
图：并行网络机器学习架构的示意图。这里我们展示了储备池2（R2），它接收来自其指定节点（节点2）的输入，加上与节点2相连的节点（即节点1和3）的输入。然后，R2被训练以预测其分配的节点（节点2）。这个过程对网络中的每个节点都是一样的，这样，储备池之间的连接就模仿了要预测的网络。
3. 湍流中物质环的统计几何学
论文题目：The statistical geometry of material loops in turbulence 论文来源：Nature Communications 论文链接：https://www.nature.com/articles/s41467-022-29422-1
图：最初的圆环（颜色对应于初始角度）在 27τη 内的湍流场平流，其中 τη 是 Kolmogorov 时间。 湍流的扭曲和折叠作用产生了复杂的环几何形状，而环的长度平均呈指数增长。 所示的循环是一个比较极端的情况。经过较长时间后，湍流较小区域中的环路会形成扩展且复杂的结构。插图为导致曲率峰值的材料折叠。
4. 基于知识提取的
通信高效联邦学习
论文题目：Communication-efficient federated learning via knowledge distillation 论文来源：Nature Communications 论文链接：https://www.nature.com/articles/s41467-022-29763-x
图：FedKD 框架，利用本地数据对 local mentor 模型和 global mentee 模型进行训练。两种模型都是从局部标记数据以及预测结果和隐藏结果中学习。本地梯度在上传到服务器之前进行分解，然后在服务器上重新构建以进行聚合。聚合的全局梯度进一步分解并分发给客户端以进行本地更新。
5. 二分网络模型
设计急性髓系白血病联合治疗方案
论文题目：Bipartite network models to design combination therapies in acute myeloid leukaemia 论文来源：Nature Communications 论文链接：https://www.nature.com/articles/s41467-022-29793-5
图：数据收集和预处理从Beat AML药物反应数据集开始，然后是关联矩阵提取、加权二分网络重建、网络投影和社区发现。使用ChEMBL、Omnipath、DrugTargetCommons和KEGG数据库，根据现有的基因表达谱、药物-靶点相互作用、蛋白质-蛋白质相互作用和生物路径，利用所有集群的药物和病人/细胞成员的相似性进行集群内同质性分析。 此外，额外的药物反应数据集GDSC和ALMANAC分别用于集群内同质性分析和集群间药物组合策略步骤，以检查所提出的工作流程是否独立于数据集。
6. 神经网络中的
Gell-Mann-Low临界性
论文题目：Gell-Mann–Low Criticality in Neural Networks
论文来源：Physical Review Letters
论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.168301
临界性与最佳计算能力有着深刻的联系。然而，到目前为止，由于缺乏大脑临界动力学的重整化理论，对这种形式的生物信息处理的理解仅限于平均场结果。这些方法忽略了临界系统的一个关键特征：跨越所有长度尺度的自由度之间存在相互作用，这是复杂的非线性计算所需要的。我们提出了一个典型的神经场理论的重整化理论，即随机的威尔逊-考恩模型（Wilson-Cowan model ）。我们计算了耦合流，它在不断增加的长度尺度上参数化相互作用。尽管与 Kardar-Parisi-Zhang 模型有相似之处，但该理论属于 Gell-Mann-Low 类型，是可重整化量子场论的典型形式。在这里，非线性耦合消失，流向高斯固定点，但对数缓慢，因此在大多数尺度上仍然有效。我们展示了这种临界的相互作用结构，以实现信息存储的最佳线性和计算所需的非线性之间的理想权衡。
图：（a）一个线性读数被训练成从神经活动中提取所需的输入-输出映射。集体非线性相互作用是实现复杂映射的基础。因此，我们需要超越平均场方法，在逐渐增加的长度尺度上跟踪非线性相互作用。(b) 方差，蓝色钻石：模拟；深蓝色虚线：线性系统；灰色实线：重整化理论。（c）耦合流，过渡线（黑色虚线）将收敛区（绿色）和发散区（红色）分开。（d）记忆，对于不同强度的非线性，高斯输入随时间的重建精度（0：完全遗忘；1：完美重建）。（e）分类，正确分配给3位字符串的奇偶性份额（蓝色曲线）和重复训练的标准偏差（阴影区）。读出时最慢（红色）、中间（橙色）和最快（绿色）模式的衰减时间尺度。
论文题目：Gell-Mann–Low Criticality in Neural Networks 论文来源：Physical Review Letters 论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.168301
图：（a）一个线性读数被训练成从神经活动中提取所需的输入-输出映射。集体非线性相互作用是实现复杂映射的基础。因此，我们需要超越平均场方法，在逐渐增加的长度尺度上跟踪非线性相互作用。(b) 方差，蓝色钻石：模拟；深蓝色虚线：线性系统；灰色实线：重整化理论。（c）耦合流，过渡线（黑色虚线）将收敛区（绿色）和发散区（红色）分开。（d）记忆，对于不同强度的非线性，高斯输入随时间的重建精度（0：完全遗忘；1：完美重建）。（e）分类，正确分配给3位字符串的奇偶性份额（蓝色曲线）和重复训练的标准偏差（阴影区）。读出时最慢（红色）、中间（橙色）和最快（绿色）模式的衰减时间尺度。
7. 生成模型学习的神经编码框架
论文题目：The neural coding framework for learning generative models 论文来源：Nature Communications 论文链接：https://www.nature.com/articles/s41467-022-29632-7
图：神经生成编码、计算和环路。（a）神经生成编码中两个重要计算步骤：（1）预测和侧向错误计算；（2）神经状态的误差-纠正。图中绘制了一个3层的简单网络，每层由2个状态神经元组成（灰色圆），在T步里迭代更新。其中两层神经元与误差神经元（橙色钻石形）连接，误差神经元计算在整个系统中传播的误差信息。底层z0接收感官输入（一张图片）。（b）神经生成编码中基本神经元计算单元，在l层里由一个状态神经元，一个误差神经元组成。在这个环路中，一个状态神经元不仅接收误差神经元的信息（由传递），还接收一个自激发信号（由传递）和侧向连接神经元传来的抑制信号（由传递）。误差神经元接收从侧向连接神经元传来的增益信号（由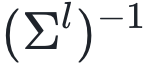传递）。（c） 该研究中采用的不同神经生成编码结构。黑色实箭头代表生成权重，黑色虚箭头代表误差权重，淡粉色虚箭头代表临时（虚拟）反向传播误差通路，这是一个生成权重的函数，即误差权重的转置（粉色水平实箭头代表哪个前向权重被用于制作反向通路权重）
关于Complexity Express
Complex World, Simple Rules. 复杂世界，简单规则。
为了让大家能及时把握复杂系统领域重要的研究进展，我们隆重推出「Complexity Express」服务，汇总复杂系统相关的最新顶刊论文。
Complexity Express 是什么？
Complexity Express 为谁服务？
-
如果你是复杂系统领域的研究者，可获得重要论文上线通知，每周获取最新顶刊论文汇总。
-
如果你是复杂系统领域的学习者，可了解学界关注的前沿问题，把握专业发展脉络。
-
如果你是传统的生命科学、社会科学等学科中的研究者/学习者，可以从复杂科学和跨学科研究中获得灵感启发。
-
如果你是关注前沿研究发现的知识猎手，可获得复杂系统研究对自然和人类世界的最新洞见。
Complexity Express 论文从哪里来？
-
Nature
-
Science
-
PNAS
-
Nature Communications
-
Science Advances
-
Physics Reports
-
Physical Review Letters
-
Physical Review X
-
Nature Physics
-
Nature Human Behaviour
-
Nature Machine Intelligence
-
Review of Modern Physics -
Nature Review Physics -
Nature Computational Science -
National Science Review -
更多期刊持续增补中，欢迎推荐你认为重要的期刊！
Complexity Express 追踪哪些领域？
-
复杂系统基本理论 -
复杂网络方法及应用 -
图网络与深度学习 -
计算机建模与仿真 -
统计物理与复杂系统 -
量子计算与量子信息 -
生态系统、进化、生物物理等 -
系统生物学与合成生物学 -
计算神经科学与认知神经科学 -
计算社会科学与社会经济复杂系统 -
城市科学与人类行为 -
科学学 -
计算流行病学 -
以及一些领域小众，但有趣的工作
更多论文
点击“阅读原文”，追踪复杂科学顶刊论文
微信扫一扫,分享到朋友圈
