导语


罗伯特·梅的稳定性理论一直是理论生态学的核心范式。该理论指出：大的生态系统能够在达到特定临界复杂度前保持稳定，这是生态系统中的物种数量及物种间相互作用强度的产物。也就是说，为了保持稳定，高度多样化的生态系统一定减少了复杂性。然而，到目前为止验证这一假设仍然十分困难。因为这涉及到如何重建庞大的生态相互作用网络，并测量其复杂性。最新发表在 Nature Ecology & Evolution 的一篇文章介绍了一个计算框架，该方法并没有直接测量生物之间的互动关系，而是试图通过对比许多生态系统的剖面（snapshot），计算生态系统的平均复杂度。作者通过计算微生物群落的复杂性，为罗伯特·梅的经典理论提供了的证据，即只要具有较低的复杂性和较弱的相互作用，具有较高多样性的微生物群落就会保持稳定。


研究领域：生态网络，复杂性，系统稳定性，理论生态学

‍‍

Akshit Goyal | 作者

郭瑞东 | 译者

刘志航 | 审校

邓一雪 | 编辑



论文题目：

Complexity–stability trade-off in empirical microbial ecosystems

论文链接：
https://www.nature.com/articles/s41559-022-01745-8

 




1. 多样性的生态系统

通过降低复杂性保持稳定？




当我们漫步于森林之中，或在礁石周围潜水时，会惊讶于生活在我们周围生物群落的惊人多样性。尽管存在对食物、阳光和其他资源的竞争，但包含数百个物种的生态系统仍然可以保持惊人的稳定。为了让生态系统的稳定共存成为普遍现象，理论生物学家罗伯特·梅（Robert May）认为，高度多样化的生态系统一定减少了复杂性——也就是说，更少或更弱的物种间相互作用[1]。
 
虽然这是该领域的核心原则，但通过实证检验生态系统是否遵守这一约束一直很困难，部分原因在于，衡量一个生态系统中的所有相互作用是一项艰巨的任务。由于缺少实证证据支持，同时还存在各种各样替代的理论，该领域对罗伯特·梅所描述的约束的有效性产生了很多争论。在Nature Ecology & Evolution 发表的论文中 ，Yonatan等人[2] 使用计算手段直接测量一个生态系统的整体复杂性，而不必知道底层相互作用结构。论文指出，生态系统可能真的像罗伯特·梅的理论描述的那样运转：更多样化的生态系统通过更少的复杂性来保持稳定。
 




2. 如何衡量生态系统复杂性？




迄今为止，生态学家衡量生态系统的复杂性时，考虑的是食物网，即对生态系统中某种生物以另一种生物为食的关系汇总。但基于食物网的定性信息，很难转换为罗伯特·梅的理论中可直接测量的、对复杂性的量化评价[3-6]。此外，测试复杂性是否随着多样性的减少而减少，需要比较不同的食物网，这可能是存在问题，因为这些食物网来自不同的实地研究，并且是用不同方法重建的。
 
Yonatan等人[2]采取了一种不同的、相当有创意的计算方法，在以前的方法基础上分析了生态系统的动力学[7]。该方法并没有直接测量生物之间的互动关系，而是试图通过对比许多生态系统的剖面（snapshot），计算生态系统的平均复杂度。这类似于比较巨大森林中的两片区域。
 

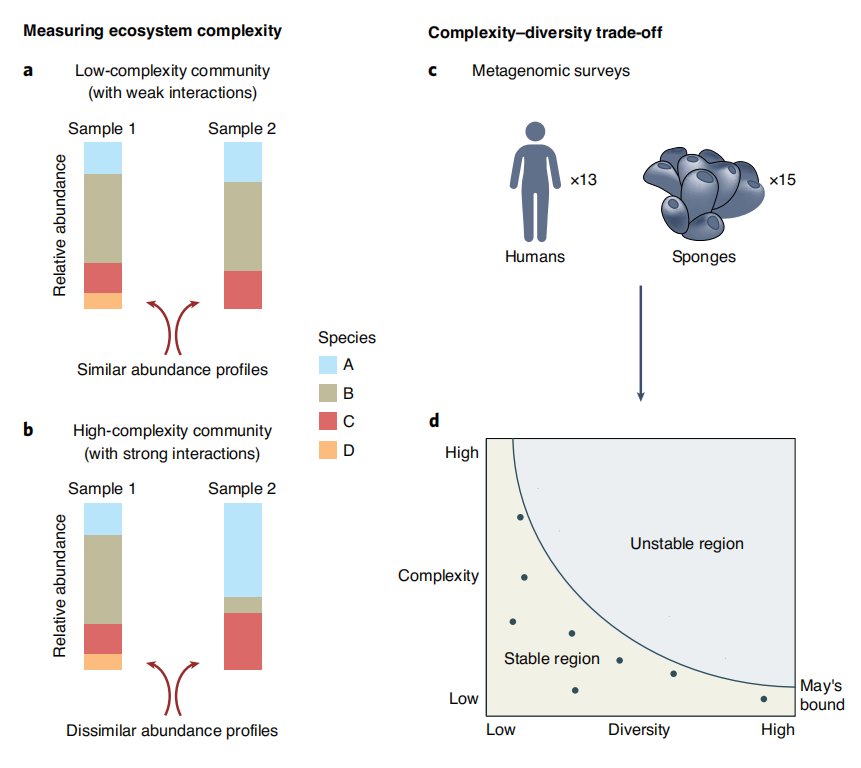
图1. 更大的生态系统，复杂度更低。漫画说明了Yonatan等人衡量生态系统复杂性的想法。作者对比具有相似物种集合的生态系统的两个剖面（物种丰度的堆积柱状图，A-D为四个物种）。（a）如同比较两个生态系统的剖面，发现一个生态系统中缺少黄色的标记为D的物种，在其他物种丰度上相似，那么这样的生态系统存在较少的相互作用，复杂度更低。（b）如果生态系统的两个剖面看起来不相似，那么黄色的物种很有可能和其他物种存在强相互作用，生态系统的复杂度高。因此，生态系统的复杂度，可以通过对多组生态系统剖面对比的平均来衡量。（c）作者使用已发表的人体不同位置的微生物群落数据，以及海洋里海绵的微生物群落，来衡量微生物群落的复杂性和多样性。（d）复杂性和多样性的散点图，其中每个点代表从相似环境中采样的生态系统。作者发现复杂性和多样性之间存在负相关：更多样的系统，复杂度更低。这一结论和罗伯特·梅关于生态系统稳定性的理论是一致的，该理论推断这样的负相关使得多样性更高的生态系统能够保持稳定。

 
该研究的关键方法学亮点，是用平均值度量复杂度，这使得研究者不必测量生态系统中所有的相互作用，类似于你不需要知道一个房间里每个气体分子的速度也可以估计气温。在罗伯特·梅的理论中，低复杂度的生态系统是指，任何物种的存在或消失都不会对生态系统其他部分的物种丰度产生重大影响，因为物种间的相互作用通常很弱（图1a）。相比之下，在一个高复杂度的生态系统中，增加或减少一个物种通常会改变生态系统的整体面貌，因为每个物种都与其他物种有强烈的相互作用（图1b）。这表明一种估计复杂性的直观方法：把它们分成几乎共享所有物种的一对（除了少数），然后比较每对之间的平均相似度。平均相似度高的生态系统可能不太复杂，而相似度低的生态系统可能高度复杂。
 
 



3. 微生物群落提供丰富数据




初看起来，对生态系统进行多次剖面观测，其中出现的物种存在差异，是一个比对食物网进行记录更为困难的工作。在这里，Yonatan等人[2]将他们的注意力转向了微生物群落，相比森林或珊瑚礁，微生物群落也存在惊人的多样性，包含数百个物种。此外，微生物体积小，意味着存在众多版本（例如不同人的肠道微生物）。目前已有很多公开的微生物测序数据库，例如人类微生物组计划[8]和海绵微生物组计划[9]，且都已转换为物种丰度信息。
 
在这个想法的激励下，作者收集了已发表的关于数十个微生物群落的宏基因组数据，范围从人体的不同部位到海洋中的海绵（图1c）。在每一个群落中，研究者使用他们新提出的计算方法估计其复杂度。结果发现在复杂度和物种个数之间存在负相关，生态系统越多样，复杂度越低（图1d）。作者们由此得出结论，这些生态系统的确满足罗伯特 · 梅理论描述的约束。
 
理论生态学的研究，一直围绕1972年罗伯特·梅提出的假设。其中一个受到质疑的假设是物种间的相互作用是随机的，而有些研究指出，结构化的相互作用会带来更稳定而非更不稳定的生态系统[10]。还有人认为，物种之间的相互作用要比罗伯特·梅假设的成对相互作用复杂得多。事实上，在生态系统的三元组中出现高阶互动，会使生态系统变得更加稳定[11]。尽管这一争论远未解决，Yonatan等人的方法完全规避了量化物种间相互作用的问题，进入了检验罗伯特·梅理论的核心，而不是提出替代方案。他们对生态系统复杂度的测量，凸显了罗伯特·梅简单而优雅的理论可能已经足够。真实的生态系统可能确实受限于稳定性约束。
 
 

论文 Abstract

May’s stability theory, which holds that large ecosystems can be stable  up to a critical level of complexity, a product of the number of  resident species and the intensity of their interactions, has been a  central paradigm in theoretical ecology. So far, however, empirically  demonstrating this theory in real ecological systems has been a  long-standing challenge with inconsistent results. Especially, it is  unknown whether this theory is pertinent in the rich and complex  communities of natural microbiomes, mainly due to the challenge of  reliably reconstructing such large ecological interaction networks. Here  we introduce a computational framework for estimating an ecosystem’s  complexity without relying on a priori knowledge of its underlying  interaction network. By applying this method to human-associated  microbial communities from different body sites and sponge-associated  microbial communities from different geographical locations, we found  that in both cases the communities display a pronounced trade-off between the number of species and their effective connectance. These results suggest that natural microbiomes are shaped by stability constraints, which limit their complexity.

  

参考文献

  1. May, R. M. Will a large complex system be stable? Nature238, 413–414 (1972).
  2. Yonatan, Y., Amit, G., Friedman, J. et al. Complexity–stability trade-off in empirical microbial ecosystems.Nat Ecol Evol  (2022).
  3. Yodzis, P. The stability of real ecosystems. Nature289, 674–676 (1981).
  4. Winemiller, K. O. Must connectance decrease with species richness? Am. Naturalist134, 960–968 (1989).
  5. James, A. et al. Constructing random matrices to represent real ecosystems. Am. Nat.185, 680–692 (2015).
  6. Schmid-Araya, J. M. et al. Connectance in stream food webs. J. Anim. Ecol.71, 1056–1062 (2002).
  7. Bashan, A. et al. Universality of human microbial dynamics. Nature534, 259–262 (2016).
  8. Huttenhower, C. et al. Structure, function and diversity of the healthy human microbiome. Nature486, 207 (2012).
  9. Moitinho-Silva, L. et al. The sponge microbiome project. Gigascience6, gix077 (2017).
  10. Dunne, Jennifer A., Richard J. Williams, and Neo D. Martinez. “Food-web  structure and network theory: the role of connectance and size.” Proceedings of the National Academy of Sciences 99.20,12917-12922 (2002).
  11. Grilli, J., Barabás, G., Michalska-Smith, M. J. & Allesina, S.  Higher-order interactions stabilize dynamics in competitive network  models. Nature548, 210–213 (2017).
 
本文翻译自  Nature Ecology & Evolution
原文题目：How diverse ecosystems remain stable
原文链接：https://www.nature.com/articles/s41559-022-01758-3


复杂科学最新论文


集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：



推荐阅读



点击“阅读原文”，追踪复杂科学顶刊论文