什么是多稳态 | 集智百科

“集智百科精选”是一个长期专栏,持续为大家推送复杂性科学相关的基本概念和资源信息。作为集智俱乐部的开源科学项目,集智百科希望打造复杂性科学领域最全面的百科全书,欢迎对复杂性科学感兴趣、热爱知识整理和分享的朋友加入!
本文是对集智百科中“多稳态”词条的摘录,参考资料及相关词条请参阅百科词条原文。
本词条由集智俱乐部众包生产,难免存在纰漏和问题,欢迎大家留言反馈或者前往对应的百科词条页面进行修改,一经修改,可以获得对应的积分奖励噢!

双稳态
在势能方面,一个双稳态系统有两个局部势能极小值,它们之间有一个局部极大值。一个双稳态的机械设备的例子是灯的开关,开关要么“开”要么“关”,但不会在二者之间停留。
在保守力场中,双稳态基于势能有三个平衡点的事实,其中两个极小,一个极大。通过数学讨论可知,极大值一定在两个极小值之间。一个处于基态的粒子位于两个平衡点中的一个,因为这对应着能量最小值。最大值可以被看作它们之间的一道屏障。
如果一个系统获得足够的活化能来穿过屏障(在化学例子中对比活化能与阿伦尼乌斯公式),那么它就可以从一个能量最小态过渡到另一个能量最小态。达到界限后,系统会在松弛时间后进入另一个能量最小态。
双稳态在数字电子设备中被广泛用于存储二进制数据。一个双稳态设备以一种状态代表“0”,另一种状态代表“1”的形式储存1比特的二进制数据。它同样被应用于张弛振荡器、多谐振荡器及施密特触发器。视觉双稳态是一些特定的视觉设备的分布,根据输入,这些设备中有两个稳定的共振的传送状态。双稳态也可以出现在生物化学系统中,它从持续的化学浓度和化学反应中产生数字式、开关式的输出。在这些系统中双稳态通常与滞后现象有关。


初始不稳定性
在经济学和社会科学中,路径依赖导致了发展方向上的分歧。一些路径的依赖过程可以通过多稳态来充分描述:在到达稳态之前,对输入的初始状态很敏感,比如最初市场份额不稳定,随后可能会演变成多个可能的供应商之一的稳定垄断。
多稳态知觉
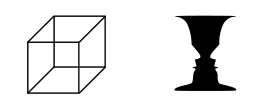
编者推荐
动力系统稳定性初步
百科项目志愿者招募
作为集智百科项目团队的成员,本文内容由舒寒参与编译,思无涯咿呀咿呀编辑。我们也为每位作者和志愿者准备了专属简介和个人集智百科主页,更多信息可以访问其集智百科个人主页。



如果你有意参与更加系统精细的分工,扫描二维码填写报名表,我们期待你的加入!

集智百科平台底层维护人员招募
为了对复杂科学做一个全面且系统的梳理,提供全面、科学、客观的基础知识,诞生了集智百科。集智俱乐部组织志愿者生产复杂科学领域的知识内容,打造复杂性科学领域的百科全书。从2013年诞生至今,百科的使命依旧继续,永不完结。
为了更好的组织协调集智俱乐部社区的力量,集智百科现开放百科平台底层维护系统。
工作职责:
-
负责集智百科的业务运维工作(e.g. 权限管理,账户管理,故障排查)
-
负责集智百科的用户体验持续提升解决方案的设计和落地(e.g. 词条编辑器体验优化,系统升级)
-
负责集智百科的服务连续性解决方案设计和落地(e.g. 容灾、监控、备份与恢复)
-
负责核心系统的代码编写、系统优化以及技术架构持续改进
-
参与开发和运维规范制定,编写相关技术文档
期望:
-
能投入一定的时间和精力参与系统维护或组内讨论(>每周1小时)
-
能积极主动地深入学习系统研发与运维相关知识
-
有一定的软件研发、运维实践经验(不论技术栈)
-
Nice to have: 有以下技术实践经验:PHP, Docker, MediaWiki, 阿里云
你可以获得:
-
投身于构建良好的学术交流氛围,改善国内科研环境,进而促进国家科技革新的伟大事业中
-
享受集智俱乐部VIP待遇(参与一年期的维护工作)
-
以练促学,践行行业最佳实践(IT行业>9年经验的前辈带)
有意向者请将个人简历发送至:avecsally@163.com
邮件抬头请写:集智百科平台底层维护人员招募
来源:集智百科
编辑:王建萍
-
什么是生态位 | 集智百科 -
量子信息与量子计算预读班:追踪量子信息革命交叉前沿 -
什么是组合博弈论 | 集智百科 -
反馈:复杂系统的自我调节机制 | 集智百科 -
动力系统中的稳定性理论 | 集智百科 -
《张江·复杂科学前沿27讲》完整上线! -
成为集智VIP,解锁全站课程/读书会
点击“阅读原文”,阅读词条多稳态原文与参考文献










