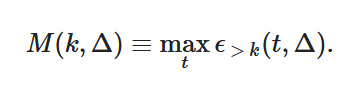识别复杂网络的隐藏组织原则和相关结构是理解其特性的根本。为此,揭开涉及网络中突出节点的结构是一种有效的方法。在时效网络中,连接的同时性是产生时间稳定结构的关键。在这里,最新发表于 Nature Physics 上的一项研究提出了一个新的衡量标准,以定量研究连接良好的节点在时效网络中形成同时性和稳定性结构的趋势。这种趋势被称为时效富人俱乐部(temporal rich club, TRC)现象。这项工作提供了一个新的程序来检测时效网络中的动态结构模式,使我们能够从一个新的定量角度来分析经济社会甚至是神经网络等不同领域的动态模式。
研究领域:复杂网络,统计物理,时效网络,动态结构

论文题目:
The temporal rich club club phenomenon
https://www.nature.com/articles/s41567-022-01634-8
通讯系统、交通基础设施、生态系统以及社会互动等各种自然和社会系统都可以被表示为复杂网络的形式,而其中的关键节点我们称之为枢纽(hub)或者是核心(core)。k-core 分解可以将网络分解为连接度越来越高的子图,在网络传播过程中的影响力也越来越大,而富人俱乐部系数则量化了枢纽是否倾向于形成更紧密的互连团体。
所谓富人俱乐部(rich club)是指网络中度值高的节点之间的连接,这些节点之间往往表现出比度值低的节点连接更加紧密的趋势,正如现实中朋友多的人往往也与朋友多的人交往更紧密。通过 k-core 分解或计算富人俱乐部系数等成熟方法都可以发现这种网络结构。但是,现实世界的大部分网络往往是动态演变的,以上基于静态网络计算的方法无法发现网络结构演变特征,产生的仅仅是时效网络的聚合表示。因此需要开发基于时效网络(temporal networks)的网络结构分析方法。
发表于 Nature Physics 的这篇文章,开发了一种针对时效网络的时效富人俱乐部系数(temporal rich club,TRC)计算方法。这种方法考虑到了网络结构形成的时效性和同时性,并能计算网络结构存在的时间跨度。给定一个时效网络,时效富人俱乐部系数量化那些与越来越多的其他节点互动的节点是否倾向于同时以稳定的方式彼此互动。
如图1 所示,考虑时间间隔 [1, T] 上的离散时效网络,表示为每个时间戳网络的一系列瞬时切片(图1a),并且 [1, T] 的时间内会聚合产生一个静态网络 G =(V, E),其中包含一组节点 V 和一组在特定时间内形成的时效边 E(图1b)。其中在两个节点 i 和 j 之间绘制一条边如果它们至少有一个共享的时效边,则权重 wij 由 i 和 j 之间的时间边的数量给出。 G 中一个节点的度数 k 是它与之交互至少一次的不同其他节点的数量,它的强度 s 是它参与的时效边的总数。
图1. 时效富人俱乐部概念图。(a)时效网络的示意图,表示为一系列瞬时切片。(b)时间聚合图,度数大于3的节点的集合 S>3 被阴影区域所突出。(c)实线表示形成 E>3的边,红色虚线表示在 t0+ Δ – 1 时活跃但在 t0 + Δ 不活跃的连边。(d)固定 k = 350 和 k = 410 时,针对美国航空运输时效网络的计算。(e)时间序列 ϵ>k(t, Δ) 与 t 的关系实例,即热力图的水平切割。
时效富人俱乐部分析目的是找到网络 G 中度数增加的节点是否倾向于在一定时间内同时连接而不是偶然连接。对于静态网络,富人俱乐部系数被定义为度数大于 k 的 N>k 个节点的子集 S>k 中的边密度。密度越大表明度数越大的节点倾向于形成连接越来越多的节点组。
对于具有时效性的动态网络,论文作者也定义了类似于静态密度的 ϵ>k值,表示在时间 [t, t + Δ] 期间内保持稳定的连接 E>k(S>k 的节点之间)的数量。然后,作者将时效富人俱乐部系数定义为以稳定的方式在 ϵ>k 值的节点中观察到的持续时间 Δ 的最大时效边密度 M(k, Δ) 。
M(k, Δ) 不仅量化了静态网络富人俱乐部模式是否对应于某个瞬间实际存在的结构,还能分析这种结构的密度以及稳定性如何。M(k, Δ) 随着 k 的增加而增加,表示在至少在 Δ 的时间内,连接最多的节点倾向于以同时的方式越来越多地相互连接,即使一个稳定的枢纽在统计上倾向于促进这种连接性。
事实上,M(k, Δ) 关注的是中心点之间的联系。此外,ϵ>k 值的时间演变表明子集 S>k的最高同时连通性时刻,以及这种连通性是稳定的还是波动的。在固定k 值的情况下,ϵ>k 值随时间 t 和持续时间 Δ 改变而改变(图1d),表现出稳定(图1e上)和波动(图1e下)的特性。
从本质上来说,时效富人俱乐部系数定义为在至少一个持续时间 Δ 内,聚合度至少为 k 的节点之间稳定的连边密度的最大值。因此,该系数衡量了动态网络的富人俱乐部结构数量的多寡以及这种结构的持续性动态。
论文作者首先将上述指标应用于描述美国航空运输基础设施,一个从2012年到2020年,时间分辨率为1个月,共105个切片的时效网络。
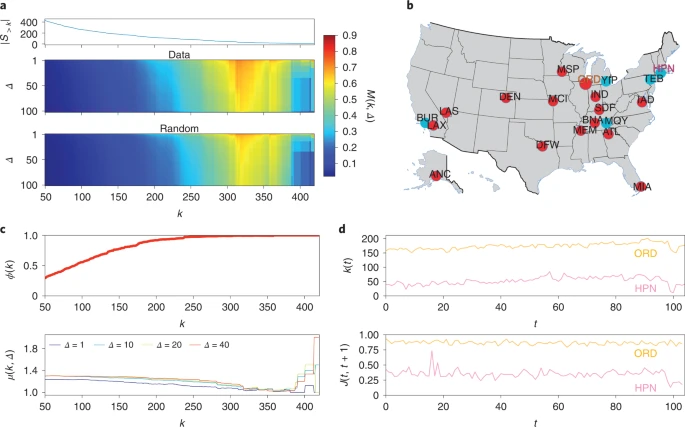
M(k, Δ) 在 k ~ 315 左右达到非常大的数值(图2a),这表明一个稳定的、非常有凝聚力的结构。事实上,在 S>135 的 31 个机场中,大部分都是美国航空运输系统的枢纽,这些机场基本上都是相互连接的,而且连接非常稳定。
但是,一些度数大于 380 的机场比其他度数为 315<k<380 的机场有更不稳定的连接,即使它们的瞬时度数保持稳定(图2d)。这种度数非常高的机场节点的反直觉行为(显示出比度数稍低的节点更不稳定的连接,也见于图1d,e),是无法从静态富人俱乐部系数的简单增加行为中推导出来的(图2c)。为什么会出现这种情况呢?
图2. (a)上图:总度数大于 k 的节点的子网络的大小 ∣S>k∣ 与 k 的函数关系;下图:其中Random 为随机的时效网络,用来与航空网络进行对比。(b)20个度最大的机场节点的地理位置(S>350)。(c)上图:节点度数的与静态富人俱乐部系数的关系;下图:节点度数的与动态态富人俱乐部系数的关系。(d)奥黑尔国际机场(ORD,橙色线)和威彻斯特县机场(HPN,紫色线)在时间 t 和 t+1 之间的节点邻域的瞬时度。这两个机场都在总度数的前20个节点中,但 ORD 有一个稳定的邻域,而 HPN 的邻域则波动较大。
图2b 显示了那些具有最大度数的20个机场节点。虽然这些红色节点是著名的枢纽,但也包括伯班克-好莱坞机场(BUR)或威彻斯特县机场(HPN)等作为作为洛杉矶(LAX)和纽约(JFK)等枢纽机场的缓解机场。它们在航空网络中的连接非常好,但根据相邻枢纽的需要,它们的连接是波动的。
图2d 强调了两种类型的节点,即“真正的”枢纽机场和缓解机场之间的差异。一方面,枢纽和缓解者的瞬时度 k(t) 都有相当稳定的值。但另一方面,HPN 机场尽管有最大的度值,但从一个月到下一个月,其邻域的变化高达80%(图2d)。
因此,时效富人俱乐部发现的模式并不能简单地从静态富人俱乐部的系数中推断出来,也不能从它们的瞬时度数的波动中推断出来。总的来说,在动态演化视角下对美国航空运输网络的分析揭示了连接良好的节点的不同作用,强调了网络结构的时效性。
第二个网络是法国一所小学的 232 名学生和 10 名教师之间面对面互动的时效网络。两个节点之间的每条时间边都对应着两个相应个体之间的面对面互动,由可穿戴传感器检测。数据的时间分辨率为20秒。
图3a 显示,网络中度数较高的节点倾向于更紧密地相互连接,而且是以一种更稳定的方式,拥有更多的联系人多样性的儿童往往更多的相互联系,并且这些节点之间的稳定结构实际上是以一种同时的方式发生的。
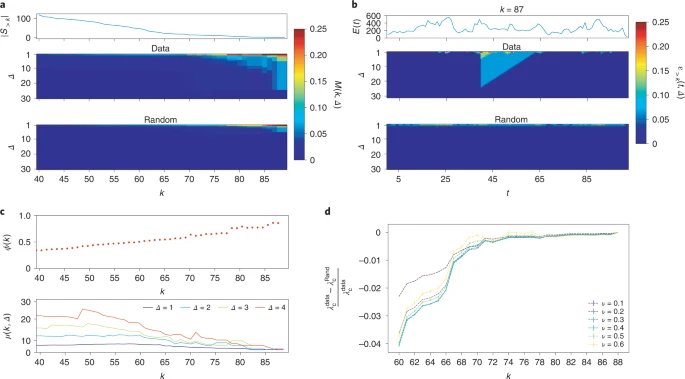
图3. 小学时间网络。(a)含义与图2a 相同。(b)上图:每个时间步的时效边的数量;中图:ϵ>87 相对于 t 和 Δ 热力图;下图:随机化数据的相同内聚力的颜色图。(c)含义与图2c 相同。(d)对原始数据集计算的传染阈值时效富人俱乐部和随机时效网络之间的相对差异。
然而,在瞬时静态富人俱乐部系数中看到的表面稳定性模式不一定对应于网络结构的真正稳定性。图3b 显示,高度数节点之间的连接结构是部分存在的,也就是说这些学生之间的凝聚结构只以稳定的方式出现一次,即在午餐时。
那么这种时效富人俱乐部结构是否会有利于信息或是传染病的传播呢?论文作者使用 SIS 和SIR 传染病模型。通过给定恢复概率 ν 时的传染阈值λc( SIS 和 SIR 模型的阈值是一致的40)来量化时效网络和传播之间的相互作用。当个传染概率大于阈值时,传染病将在所有个体中传播。通过与随机时效网络进行对比发现(图3d),时效富人俱乐部结构更有利于传播过程,也就是说,与随机时效网络相比,连接的同时性更强。因此,TRC 分析揭示了影响传播动力学的突出节点的内聚同时性结构,类似于枢纽或其他结构的波动或稳定性。
作者最后研究了麻醉大鼠的内皮层和海马中 N=67 个神经元的时间分辨功能连接的时效富人俱乐部模式。节点代表神经元,时效边对应于10 秒中成对神经元放电模式之间的信息交流(图4a)。连续的时间窗口移位1 秒,就是网络的时间分辨率,持续了2284秒。
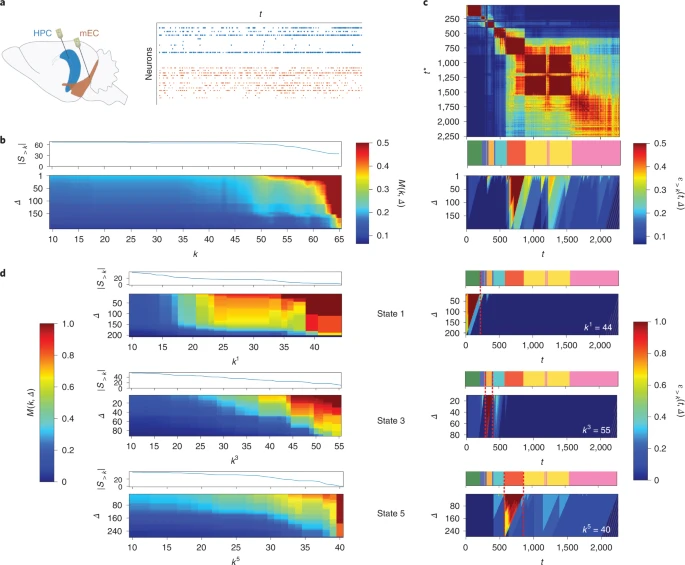
图 4. 信息交流神经元的时效网络。(a)脑区简图。(b)时效富人俱乐部系数 M(k, Δ) 随 k 和 Δ 的变化而变化。(c)时效网络相似性矩阵,是由时效网络的瞬时切片之间的相似性给出。对角线周围的红色块表示网络与自身保持相似的时期,也就是网络的“状态”。这些状态的时间线在矩阵下方显示为彩色条码(每种颜色代表不同的状态)。(d)对于三个不同的状态(状态1、3和5),度大于k的节点的子网络的大小 ∣S>k∣ 和 M(k, Δ) 的关系热力图。
考虑到时间性,就会发现一个更有趣的情况。图4b显示,对于每个持续时间 Δ,时效富人俱乐部系数 M(k, Δ) 随着 k 的增加而增加,并且 k 增加的节点组在越来越长的时间内同时相互连接。度数最大的 8 个神经元组以同时和稳定的方式非常强烈地相互连接(M(k, Δ)≥0.5)直到Δ=150。也就是说,在静态聚集图中看到的这8个神经元的完全连接链接结构确实在某个时间以同时的方式发生。
对应于整个时效网络上计算的时效富人俱乐部,神经元功能连接经历了几个“状态”。这些状态由网络相似性矩阵的分层聚类确定(图4c)。“状态”是指相似度值较大的时期(图 4c 中沿对角线的红色块,下面是连续状态的时间轴)。即使时效富人俱乐部分析本身并不能揭示不同网络状态的确切含义,但其结果至少表明,神经元网络中存在一个稳定期,并且在特定的时间段具有明显的动态。这种状态的发现,不仅仅有助于识别神经信息处理的关键过程,如突触可塑性,还能确定受到神经元相互作用时间的关键影响。
在一个细胞集合体中,许多神经元必须在一定时间内保持强烈的功能连接,以使集合体被检测到。这种放电协调(在空间上的分布和时间上的持续)只能被普通的方法部分地捕捉到,这些方法要么寻求瞬时同步,要么寻求顺序放电。而时效富人俱乐部概念抓住了将一组共时的神经元定性为一个集合体所需的两个标准。
因此,时效富人俱乐部指标能够加入网络神经科学的工具箱,用于研究动态功能连接模式。总之,这项工作提供了一个新的程序来检测时效网络中的相关时间和结构模式,使我们能够从一个新的定量角度来看待来自非常不同领域的数据集的时间模式。
随着对现实世界的探索不断深入,人们发现在许多真实的复杂系统中,组成系统的个体之间不仅存在二元交互关系,也广泛存在多个体同时(或以特定顺序)进行交互,即高阶交互现象。为此,研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型,为复杂网络分析和研究提供了新的思路。为了促进此领域的交流与合作,我们发起了【高阶网络读书会】。
集智俱乐部读书会是面向广大科研工作者的系列论文研读活动,其目的是共同深入学习探讨某个科学议题,激发科研灵感,促进科研合作。【高阶网络读书会】由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学(北京)管青老师联合发起,第一期分享从 6月 28日(周二)20:00 开始,后续每周分享时间为每周四 19:00-21:00 进行,预计持续 10-12 周。这其间,我们将围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨,本次读书会分享会按照「基础理论」+「深入理论」+「案例研讨」的模式展开。