数字货币市场为何快速更迭?生态系统理论争相解答

导语
自2008年第一种数字加密货币比特币推出以来,加密货币市场在市值和货币数量方面都出现惊人增长,这一成功引起了经济学家的强烈兴趣。研究者们提出一种视角,将加密货币市场视为一个生态系统。2022年4月发表于 Royal Society Open Science 的最新研究进一步在加密货币市场和生态系统之间建立类比,利用宏观生态理论以更好地阐明加密货币市场的群落结构,考察加密货币之间的相互依赖性和相关性。这些分析将为理解加密货币市场带来新见解。
集智俱乐部正在组织复杂经济学读书会第二季,由北京师范大学李红刚、王有贵、张江、陈清华老师以及中山大学袁先智老师联合发起。从7月11日起,每周一晚举办研讨分享,预计持续 10-12 周。我们将围绕复杂经济学的内涵、基本方法、普适规律、应用场景四个方面进行探讨,并计划组织三次圆桌讨论,与国内外学者进行深入探讨。欢迎感兴趣的朋友报名参与,详情见文末。
研究领域:加密货币市场,宏观生态理论,市场生态学

Edgardo Brigatti, Estevan Augusto Amazonas Mendes | 作者
夏鑫雨 | 译者
梁金 | 审校
邓一雪 | 编辑

论文题目:
Testing macroecological theories in cryptocurrency market: neutral models cannot describe diversity patterns and their variation
论文链接: https://royalsocietypublishing.org/doi/10.1098/rsos.212005
1. 引言
1. 引言
2. 数据
2. 数据
3. 方法
3. 方法
 ,如果选择变量log(x),则等效于正态分布。这种分布在生态学文献中有着悠久的使用传统[25],它是SAD的合理和简洁的零假设[26],可以从基于中心极限定理[27]的纯统计非生物学论证中获得,也可以由种群模型中物种之间的生态位或种群统计差异产生[28]。总而言之,用Fisher分布来描述SAD将支持中性动力学的想法。相比之下,对数正态分布表明存在其他类型的种群动力学或纯统计机制。
,如果选择变量log(x),则等效于正态分布。这种分布在生态学文献中有着悠久的使用传统[25],它是SAD的合理和简洁的零假设[26],可以从基于中心极限定理[27]的纯统计非生物学论证中获得,也可以由种群模型中物种之间的生态位或种群统计差异产生[28]。总而言之,用Fisher分布来描述SAD将支持中性动力学的想法。相比之下,对数正态分布表明存在其他类型的种群动力学或纯统计机制。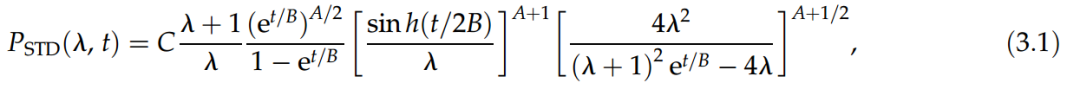
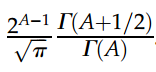 。
。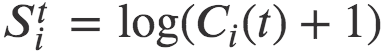 (为了避免0对数而添加1),其中t是给定的月份。请注意,对于可以用对数正态分布粗略描述的量,对数变换是一种自然方法。下一步是估计对数变换数据的皮尔逊相关性:
(为了避免0对数而添加1),其中t是给定的月份。请注意,对于可以用对数正态分布粗略描述的量,对数变换是一种自然方法。下一步是估计对数变换数据的皮尔逊相关性: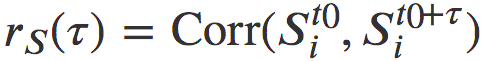 ,其中相关性是在指标i上计算的。这种方法是众所周知的[32,33],并且很容易支持显著性检验:0表示完全随机性,并且是显著性检验的零假设。总而言之,我们通过观察rS的时间衰减的功能形式来表征群落相似性演化模式,它描述了从完全相关结构到完全不相关结构的转变。
,其中相关性是在指标i上计算的。这种方法是众所周知的[32,33],并且很容易支持显著性检验:0表示完全随机性,并且是显著性检验的零假设。总而言之,我们通过观察rS的时间衰减的功能形式来表征群落相似性演化模式,它描述了从完全相关结构到完全不相关结构的转变。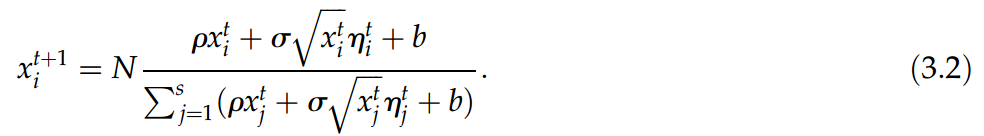
4. 结果
4. 结果
-
在2014年6月1日之前,数量辐射(mass radiation)阶段,其特征在于由非常多的物种形成事件引起的加密货币数量的惊人增加。这一阶段的特点是波动很大。 -
在2014年11月2日至2017年4月30日之间,我们可以突出显示一个平稳阶段(stationary),具有可比的物种形成和灭绝率。 -
从2017年5月7日开始,正向趋势(positive trend)是新阶段的特征,加密货币的数量以渐进和规律的方式略有增长。此外,这一阶段呈现出物种形成率相对于灭绝率更高。
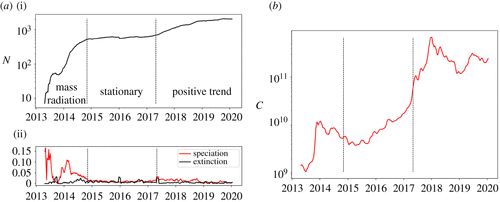
图1.(a)活跃加密货币交易量(i),给定一周内的物种形成和灭绝率,使用四周的滚动平均值(ii)。虚线垂直线表示静止阶段的开始(2014年11月2日)及其结束(2017年4月30日)。(b)市值的四周滚动平均值。
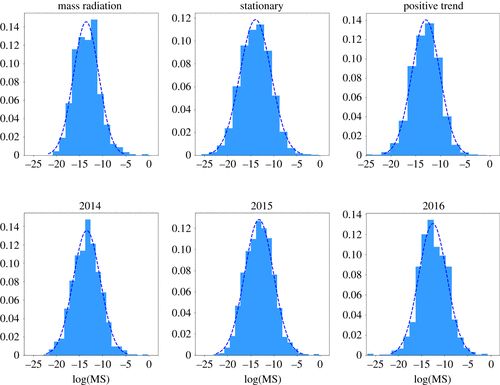
图2. 物种丰度分布对不同时期的经验数据进行采样。上图:在数量辐射期、平稳期和正趋势期采样的数据。对于表示652、1291和2825个元素的数据集,Kolmogorov–Smirnov 检验的 p 值为 0.584、0.626、0.245。下图:从2011年11月开始的平稳期收集的数据,以及1年采样的数据。对于呈现840、866和1170个元素的数据集,Kolmogorov-Smirnov 检验的 p 值为 0.996、0.715、0.253。
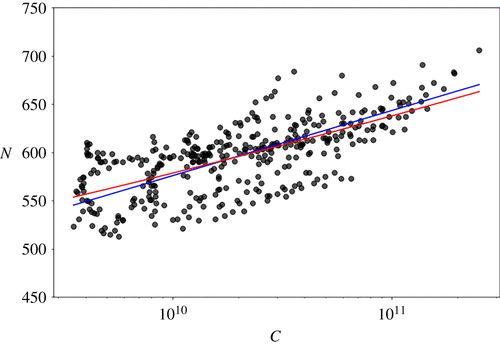
图3. 市值与物种数量的对数线性图。红线是根据关系式 αlog(1 + (x/α)) 获得的最优拟合,蓝线是根据幂律获得的最优拟合。
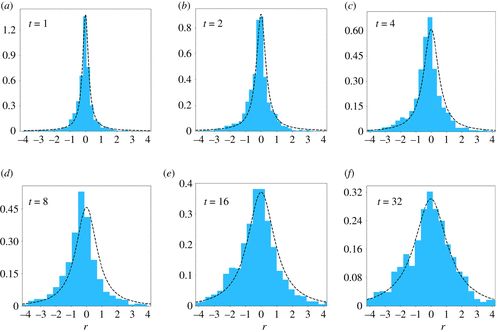
图4. 考虑到加密货币的市场份额,评估了物种更替分布。我们固定 t=1,2,4,8,16,32 周。我们考虑变量 r=log(λ) 并绘制分布 P′(r) =PSTD(er, t),其中 PSTD(er, t) 由等式(3.1)给出。最优拟合由虚线表示。
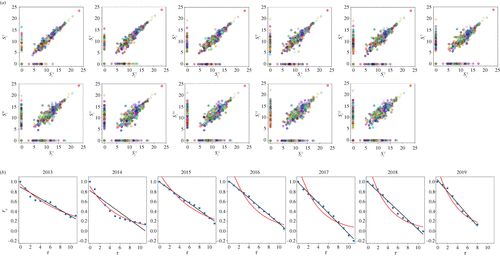
图5. (a) 初始群落中对数丰度与以下特定时间丰度(以月为单位)的散点图。显示从 2015 年 4 月 28 日到 2016 年 4 月 28 日期间的数据。结果,最初稀有或不存在的物种出现在x轴附近,稀有或灭绝的物种出现在y轴附近。请注意,许多加密货币是如何消失的。不同的颜色对应不同的货币。(b) 群落结构指数 rS 在1年内的演化。数据从2013年4月28日开始。连续黑线是最佳拟合的线性函数;红线表示指数拟合。请注意,通常,相关性表示正值。无论如何,可以达到负值,作为物种围绕x轴和y轴的最终积累的产物。
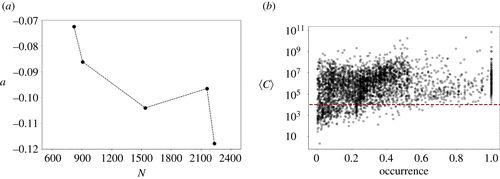
图6. (a) 2015 年至 2019 年图 5 中考虑的五个时间区间内,最优拟合线性函数(a)与活跃加密货币数量(物种丰度)的回归斜率。第一个量是时间β多样性(物种更替,即物种构成的时间变化)的度量,第二个量是α多样性的度量。(b)特定加密货币的发生与平均市值的散点图。评估数据时考虑了从静止周期开始到数据集结束的间隔。
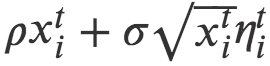 取零值时,将计入这些事件。从这些人工数据中,我们可以得到 rS 值。我们对 N, ρ 的不同值和
取零值时,将计入这些事件。从这些人工数据中,我们可以得到 rS 值。我们对 N, ρ 的不同值和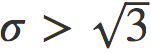 进行了大量模拟。对于此范围的参数值,模型仅生成指数衰减。图7显示了特定参数的典型示例。
进行了大量模拟。对于此范围的参数值,模型仅生成指数衰减。图7显示了特定参数的典型示例。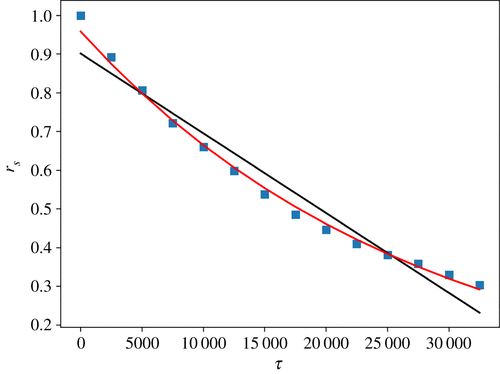
图7. 典型的 rS 从中性方程模型(3.2)生成的人工数据中获得的衰减。在这种情况下,模型参数为:N = 107, ρ = 3.5 ,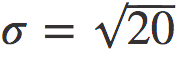 ,b = 1, s = 1500;τ 以模拟时间表示。连续黑线是线性拟合,红线是指数拟合。
,b = 1, s = 1500;τ 以模拟时间表示。连续黑线是线性拟合,红线是指数拟合。

图8. 上图:所有考虑的加密货币(左图)和前25种(右图)的相关矩阵图。加密货币从最小到最大市值填充矩阵(考虑的市值是平稳期的总市值)。请注意,高市值的加密货币对(由红色方块突出显示)通常如何呈现更高的相关性。下图:左侧的蓝色是所有考虑的加密货币(a)和前25种(b)货币对的相关性分布。红色表示从随机序列获得的相同分布。在右边,τ = 1的时间自相关是加密货币平稳期内聚合市值的函数。虚线表示在 10 个不同实现中估计的随机化数据自相关分布的 1/99 百分位。
5. 讨论
5. 讨论
数据获取路径 本文中使用的所有数据都可以从Coin Market Cap下载。下载过程可从以下位置访问: https://coinmarketcap.com/all/views/all/
参考文献
(参考文献可上下滑动查看)
复杂经济学读书会第二季招募中
经济学理论的发展与社会环境变化密切相关。一方面,伴随计算机的发展,相应的研究技术日渐成熟,例如非线性动力学、复杂网络、ABM等,为研究者提供了更强大的分析工具;另一个方面,对“均衡”的经济学的研究,不能够解释实际的经济现象,例如金融危机、创新产生的新的发展模式等,研究者开始重视经济学的“非均衡”现象,把经济系统看做复杂系统,并力图做出更能反映现实的研究。经济学内慢慢出现了一种基于更加现实的假设的研究进路,复杂经济学一个新的经济学框架正在形成。为了促进此领域的交流与合作,我们发起了复杂经济学读书会。
复杂经济学读书会第二季由北京师范大学李红刚、王有贵、张江、陈清华老师以及中山大学袁先智老师联合发起,从7月11日起每周一 19:00-21:00 进行,预计持续 10-12 周。我们将围绕复杂经济学的内涵、基本方法、普适规律、应用场景四个方面进行探讨,并计划组织三次圆桌讨论,与国内外学者进行深入探讨。热诚欢迎对复杂系统研究和经济学感兴趣的学生和学者加入这个读书会,一起探索和探讨经济复杂系统的真谛!

推荐阅读
-
Brian Arthur长文综述:复杂经济学的基础 -
AI 经济学家:从税收公平到新冠政策 -
社会物理学:探索社会经济复杂系统的百年历程 -
《张江·复杂科学前沿27讲》完整上线! -
成为集智VIP,解锁全站课程/读书会 -
加入集智,一起复杂!










