摘要


耦合振子同步进程中一级相变的涌现为理解众多复杂系统功能的转换与突变提供了重要的理论视角。近日发表在Physical Review Research上的一篇快报，揭示了耦合相振子系统一级相变的动力学起源。作者给出了异质性耦合系统一级相变产生的一般判据并解析给出各类平衡态的本征谱结构。这为进一步理解真实网络中结构扰动与功能突变的内在联系提供了重要理论启示。


研究领域：复杂系统，同步，耦合振子

徐灿 | 作者

邓一雪 | 编辑


 

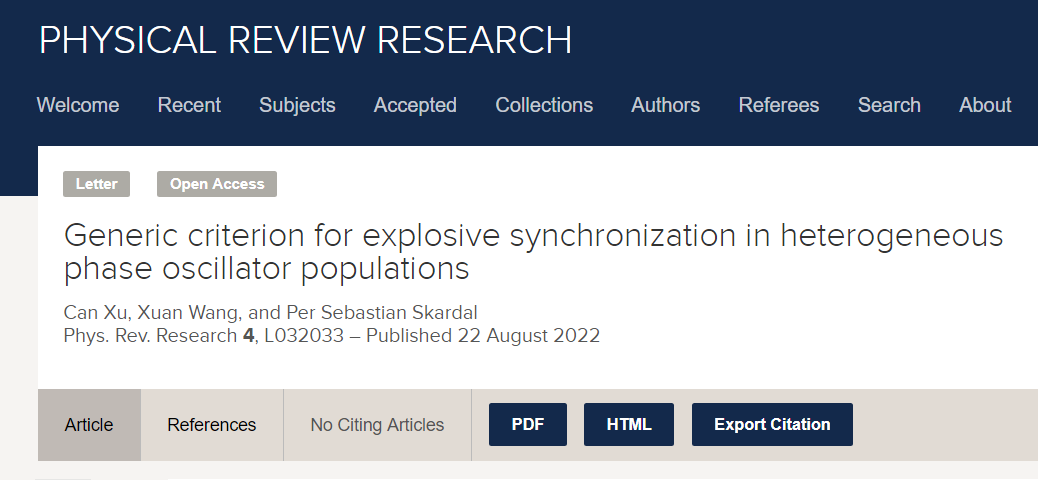
论文题目：

Generic criterion for explosive synchronization in heterogeneous phase oscillator populations
论文链接：
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.4.L032033


复杂系统不同的功能可抽象成有序和无序两类状态，从大脑中的活跃（active）-静息（rest）态到电网的运转与崩溃。深刻理解这些功能之间突变以及涌现的内在机制是复杂性科学的一个重要课题。从耦合振子的视角，这些功能的转换与突变可由同步进程中一级相变的涌现刻画。即当改变外界控制参量（如耦合强度）时，系统会经历有序到无序的突变（非连续）并伴有磁滞。双（多）稳态在磁滞区内共存，各个吸引子在相空间的吸引域由它们之间的非稳态分隔。

基于一类广义异质性耦合相振子系统，通过引入耦合与自然频率（振子内禀动力学）一般关联，研究者系统揭示了一级相变的动力学本质。解析给出了各类平衡态基于Ott-Antonsen扰动流形的本征谱结构，严格证明无序态局域分岔方向，从而建立一级相变涌现的精确判据。

根据同步研究的经典范例（Kuramoto模型）研究者将振子间的均匀耦合强度推广至自然频率的一般函数（异质性）。首先，利用平均场方法构造平衡态特征函数并结合其几何特征解析给出系统相变的临界点。对特征函数做逐级微扰展开，并利用自洽方程平衡条件定量确定序参量的标度和局域分岔特性。其次，基于平衡态Ott-Antonsen不变流形的一般形式，推导连续性方程线性演化的本征谱自洽方程，解析给出各类平衡态本征谱（包括连续谱和离散谱）结构。最后，将有序平衡态失稳条件（最大非零本征值穿越虚轴）与特征函数几何性质构建联系，得到系统一级相变（序参量亚临界分岔）产生的精确判据。


这一研究表明，一级相变的涌现要求振子频率分布与关联函数在临界点处呈负相关。如图所示，当固定频率分布时，通过改变关联函数在临界点处的二阶导数，可实现系统由二级到混合再到一级相变的转变。在网络分析中，频率关联函数可以表征动力学节点的度，这就从理论上解释了先前广泛报道的频度关联诱导一级相变。在实际应用中，这一结论为预防和控制电网崩溃的方案设计提供了理论借鉴。

如何将这一理论判据推广至真实网络，并超越平均场框架，系统揭示一级相变涌现的一般条件有待进一步探索。这些研究也将会为进一步理解和揭示复杂系统结构扰动与功能突变之间的内在联系提供重要的理论指引。

同步涌现作为一类极具代表性的自组织协同行为，是该领域的一个重要研究方向，而高阶交互耦合在同步涌现中起到关键的作用，振子间表征多对多关系的高阶交互也在物理、工程、生物等网络被揭示。同步是理解许多复杂系统宏观自组织行为的理论基础。我们讨论的主题不同于传统的连续二级相变，非连续一级相变是众多复杂系统实现其功能突变的基础，这也为进一步研究电网的级联崩溃、流行病的爆发以及癫痫病的发作等突发事件提供新的理论视野。


高阶网络读书会启动


随着对现实世界探索的不断深入，人们发现在许多真实的复杂系统中，组成系统的个体之间不仅存在二元交互关系，也广泛存在多个体同时（或以特定顺序）进行交互，即高阶交互现象。为此，研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型，为复杂网络分析和研究提供了新的思路。为了促进此领域的交流与合作，我们发起了【高阶网络读书会】。


集智俱乐部读书会是面向广大科研工作者的系列论文研读活动，其目的是共同深入学习探讨某个科学议题，激发科研灵感，促进科研合作。【高阶网络读书会】由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学（北京）管青老师联合发起，每周分享时间为每周四 19:30-21:30 进行，预计持续 10-12 周。这其间，我们将围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨，本次读书会分享会按照「基础理论」+「深入理论」+「案例研讨」的模式展开。



详情请见：

探索复杂系统高阶交互的奥秘 | 高阶网络读书会启动



推荐阅读



点击“阅读原文”，报名读书会