前沿进展:宏观麦克斯韦妖背后的热力学几何原理
导语
热力学强烈限制了静态宏观热扩散系统中的热流动方向,使用时空调制系统能够克服这种限制。近日,科学家提出了时空驱动热扩散的一般理论,揭示了宏观驱动热扩散中潜在的由冷到热的几何热泵效应以及实现热非互易性的限制条件,并实验观测到了理论所预测的几何热效应。该项研究展示了时空调制下热作用的约束定理并且能够指导驱动方式的优化。相关成果以“Geometric heat pump and no-go restrictions of nonreciprocity in modulated thermal diffusion”为题作为Letter发表于统计物理学重要期刊Physical Review E。
研究领域:统计物理,几何热泵效应,非互易性,热扩散

陈江芷 | 作者
邓一雪 | 编辑

论文题目:
Geometric heat pump and no-go restrictions of nonreciprocity in modulated thermal diffusion
论文链接:
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.106.L032102
1. 热力学定律与麦克斯韦妖
1. 热力学定律与麦克斯韦妖
热力学第二定律指出,在无外界环境影响的情况下,热流总是从高温区域自主流向低温区域,导致系统的熵增加。这一定律不难理解,比如我们将一杯热水和一杯冷水紧贴在一起,忽略外界环境的影响,一段时间后冷水的温度升高,热水的温度降低。热力学第二定律同时也适用于其它性质的流,例如在稳态下,粒子沿着浓度下降的方向流动。
很长一段时间以来,科学家们都在试图突破热力学第二定律的限制,制造出所谓的“永动机”。1871年,著名的数学物理学家麦克斯韦提出了一个新奇的热力学模型——麦克斯韦妖。简单来说,这个模型置于一个完全封闭且绝热的容器当中,这个容器从中间被隔热材料分成两半,而“妖”负责在中间位置进行管理。只要“妖”认为可以通过的粒子才能通过中间闸门进入另一半,于是冷、热分子被完全分隔在两边,从而形成巨大的温差,而人们可以利用这种温差来做功。“妖”的存在被视为是无限渺小的,中间闸门的质量也近似为零,于是“妖”开关闸门所做的功也近似为零。
2. 时间驱动系统
2. 时间驱动系统
尽管麦克斯韦妖的模型设想很难在实践上进行验证,但是对于放松热力学第二定律的限制,人们并不是无计可施。科学家们发现,通过打破系统平衡和非平衡稳态(non-equilibrium steady state, NESS)条件,可以打破热力学第二定律对热力学偏压下两端流动方向的限制。这可以通过驱动与时间相关的参数来轻松实现。
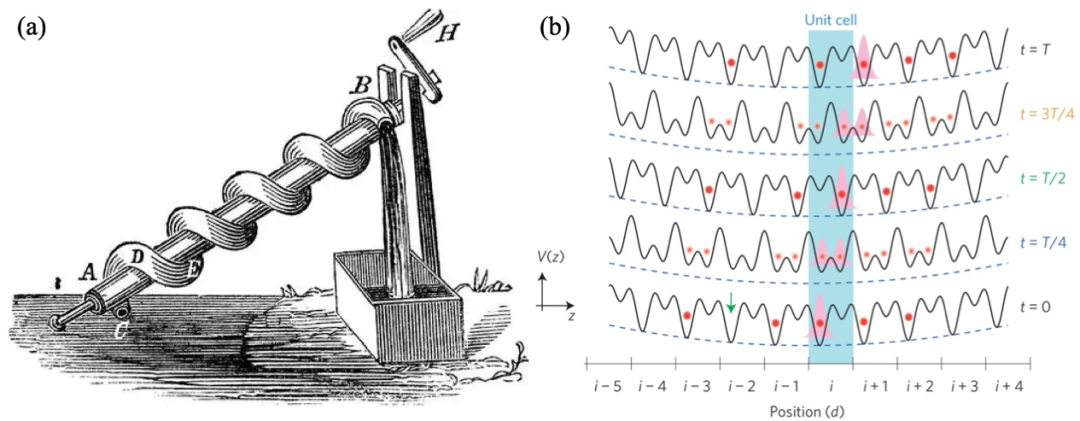
早在古希腊时期,阿基米德发明了阿基米德泵(图1a),当泵轴转动时,液体一方面随着螺杆绕轴线旋转,另一方面又沿衬套内表面滚动。螺杆每转一周,密封腔内的液体向前推进一个螺距,随着螺杆的连续转动,液体从一个密封腔被压向另一个密封腔,最后挤出泵体。因此,阿基米德泵能够实现将水从低处运往高处。
近些年来,随着纳米制造和精确控制手段的成熟,人们的研究逐渐集中到了非平衡的小系统中。时间驱动被广泛应用在量子系统和热系统中,从而产生一些新的效果,比如棘轮热流 [1]、非互易热超材料[2]、非绝热泵浦[3]等。如果不依靠时间驱动,经典的准静态过程虽然一般可以保证能量转换效率最高, 但它的长时间功率却趋向无穷小,因而很难被实际利用。与静态框架相比,受到时间驱动的系统具有更大的可调空间,它们所发挥的功能和品质参数可以通过设计特有的驱动方案得到便捷的调节。但是,时间驱动系统的研究难度也更大,特别是在对系统品质参数进行优化时,往往需要较大的计算量。因而关于受驱动系统的普遍性概念和一般理论就尤为重要。
3. 热力学几何
3. 热力学几何
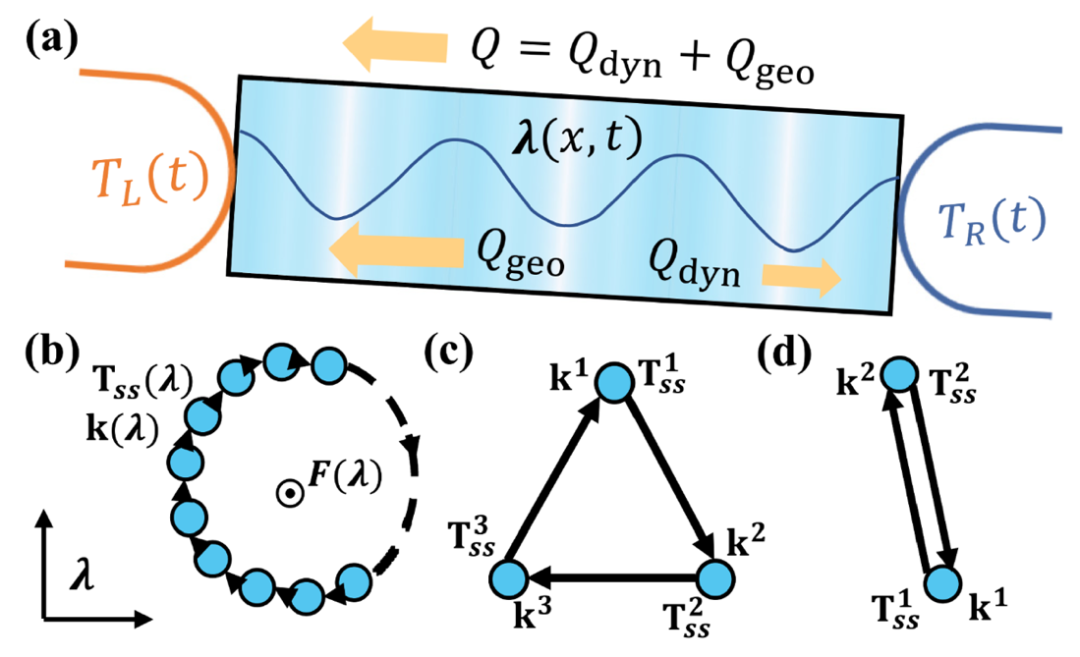
热力学几何为人们设计时间驱动系统提供了崭新的思路。几何是物理系统的一种重要内禀性质。几何相位(Berry相位)的深刻思想,引发了一场旨在定义规范不变几何可观测值并阐明其在时间驱动系统中的作用的研究热潮,其中最重要的例子之一是Thouless泵[4,5](图1b)。Thouless泵可以直观地被理解为阿基米德泵的量子版本,它在几何表达式中描述了沿一个绝热驱动周期积分的线性响应电子跃迁,当系统处于非平凡零温绝缘相时,该线性响应电流是拓扑量子化的。除了研究粒子流,这一范式也被推广到研究周期驱动中热流等能流的输运情况。基于随机热力学的研究方法,科学家借用Thouless泵和几何相位的思想,提出了量子分子结的声子热输运中,驱动热库温度等参数可产生几何相热流的热泵[6]。随后,几何相热流也在经典布朗系统[7],自旋-玻色系统[8,9],量子光力系统[10]等大量系统中得到了广泛研究。与周期驱动系统热输运和热力学几何相关的更多内容,感兴趣的读者可以参考相关的综述文章[11,12]。
然而之前的研究中,几何热泵效应的理论只被定义在量子纳米级和微观随机系统中,且尚未被实验观察到。因此,鉴于在宏观尺度上人们对非互易时空热装置的广泛兴趣,自然产生了如下基本问题:几何热泵效应是否普遍存在于受驱动的宏观热扩散中?几何热泵和热非互易性限制的一般理论是什么?如何从宏观上通过实验观察该热力学几何的效应?
4. 宏观热扩散中的几何热泵效应
4. 宏观热扩散中的几何热泵效应
为了解决上述问题,同济大学声子学中心的科学家任捷课题组[13]提出了时空驱动热扩散的一般理论,揭示了驱动宏观扩散系统中的一种新机制。通过考虑系统参数空间的内禀几何结构,研究人员挖掘出了除了传统的热-到-冷动力学热流之外,如何涌现出“反常”的从冷-到-热的“几何”热流。这种框架看起来就像是宏观的“麦克斯韦妖”。
对于经典的热扩散,中间系统温度的态矢量为Tc,热库的温度的态矢量为Tb,根据傅立叶定理和连续性方程,系统温度的态矢量演化遵循: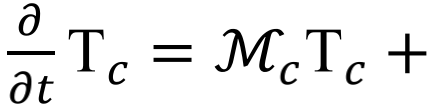
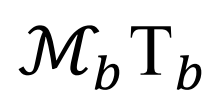 ,其中
,其中 ,C是热容矩阵,D是负散度矩阵,Kc和Kb分别是中间系统自身以及和两边热库耦合的热导矩阵。对于非绝热且周期驱动的系统来说,研究者们提出一个驱动周期τp内所积累的热量由动力学项和几何项两部分组成(图2a),并给出表达式:
,C是热容矩阵,D是负散度矩阵,Kc和Kb分别是中间系统自身以及和两边热库耦合的热导矩阵。对于非绝热且周期驱动的系统来说,研究者们提出一个驱动周期τp内所积累的热量由动力学项和几何项两部分组成(图2a),并给出表达式:
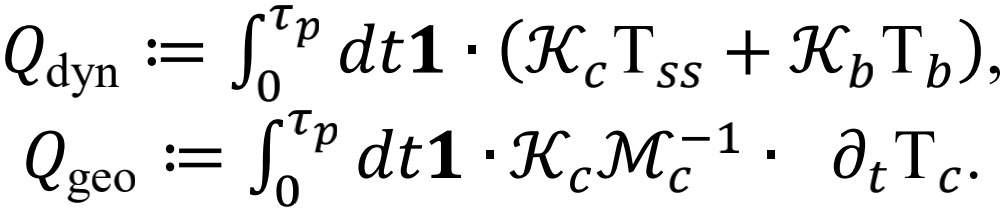
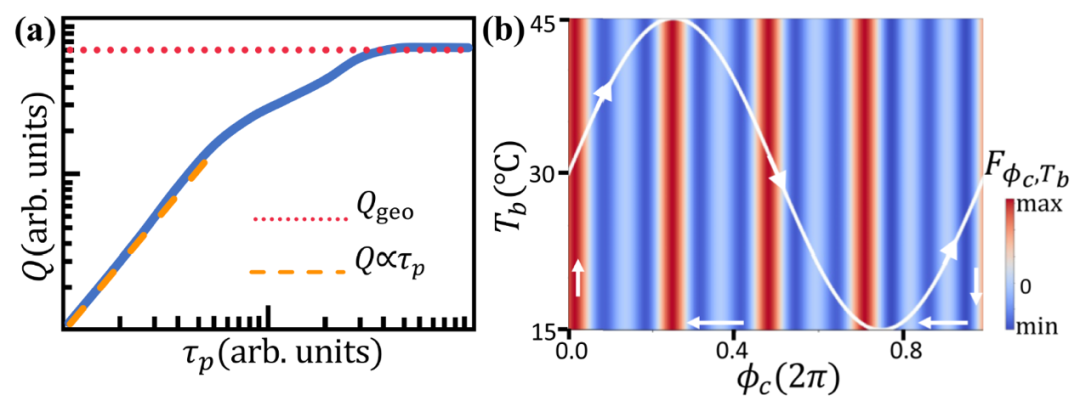
这里Tss是系统的瞬时稳态温度,1是将热流投影到感兴趣的分量上的恒定矢量。研究者们证明在有限频率极限附近的快速驱动模式下,几何项Qgeo消失,动力学项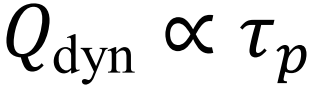 保留(图3a)。在慢驱动模式下,中间系统温度Tc达到瞬时稳态Tss,几何项Qgeo与驱动周期τp无关,该几何热可以表达为一个纯粹的几何曲率的积分:
保留(图3a)。在慢驱动模式下,中间系统温度Tc达到瞬时稳态Tss,几何项Qgeo与驱动周期τp无关,该几何热可以表达为一个纯粹的几何曲率的积分:
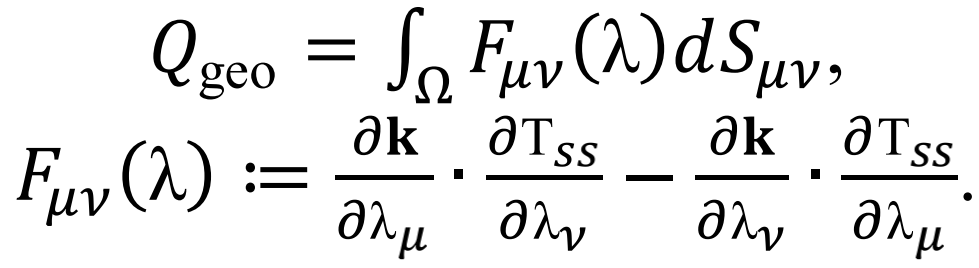
其中λ是组成闭合路径∂Ω的驱动参数,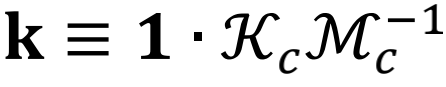 。非对称张量Fμν(λ)=-Fνμ(λ)显然具有几何曲率的含义(图2b),该区域Ω由闭合路径∂Ω包围,dSμν是表面元素。当驱动周期足够大时,几何热达到饱和值(图3a)。如图3b所示,几何热由箭头轮廓包围区域的非平凡几何曲率Fμν得出。
。非对称张量Fμν(λ)=-Fνμ(λ)显然具有几何曲率的含义(图2b),该区域Ω由闭合路径∂Ω包围,dSμν是表面元素。当驱动周期足够大时,几何热达到饱和值(图3a)。如图3b所示,几何热由箭头轮廓包围区域的非平凡几何曲率Fμν得出。
5. 泵浦“不可行”理论对热非互易的限制
5. 泵浦“不可行”理论对热非互易的限制
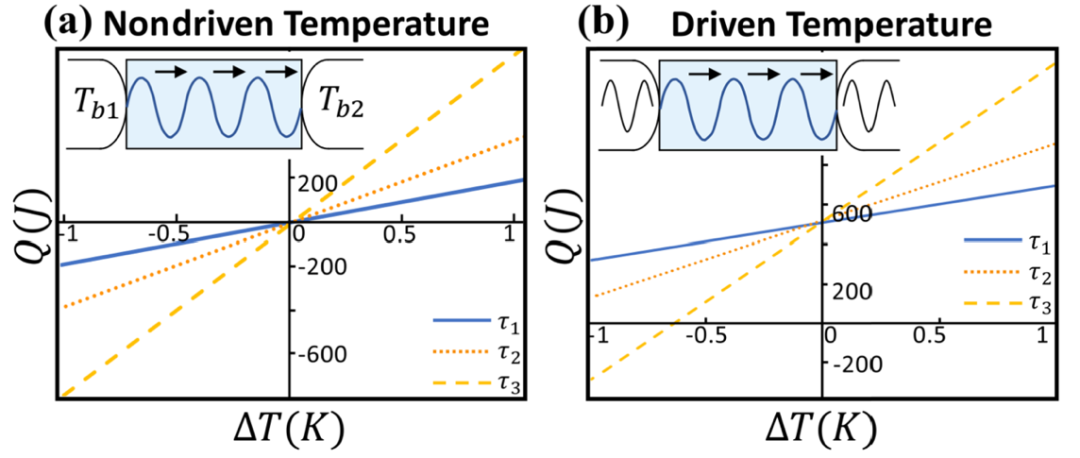
基于上述给出的几何理论,研究者们进一步推导了几何热泵效应的“不可行”限制条件。结果表明,同时调制热导和热库温度,或另外调制热容时,才能产生非平凡的几何曲率Fμν,从而产生几何热。如图4a所示,仅驱动热导并不能产生几何热泵,且这种情况下热输运是互易的。反之如图4b,同时驱动热导和热库温度变化能产生几何热泵和非互易热输运,说明非零几何热是产生热非互易性的天然资源。注意这与热力学第二定律并不矛盾,因为动力学部分和几何部分产生的总熵增总是非负的。
6. 通过实验观测宏观几何热泵效应
6. 通过实验观测宏观几何热泵效应
研究者们设计了一个离散极限条件下的实验来观察宏观热扩散系统中的几何热泵。如图5所示,周期性驱动两端热库的温度变化并保证两端热库温度始终保持一致(这样两边温差为零),同时通过记忆合金驱动中间系统与两端热库之间的耦合热导周期性变化。经过一个稳定周期后,可以测量出一个周期内的累积热量。实验结果数值上与理论提出的热量表达式基本吻合,且明显表现出在慢驱动极限下,一个周期内的累积热量为几何热饱和值,很好地验证了本文第4小节中的几何热泵一般理论。

7. 总结与展望
7. 总结与展望
通过建立时空驱动的宏观热扩散的内禀几何理论,科学家们提出了确定几何热泵浦的方法,并基于此设计构造非互易性热传输。通过设计动态调控系统,几何热可以作为生成定向热流、利用热能和生成热非互易性等方面的可靠资源。最后值得强调的是,该工作提出的理论不仅适用于热扩散,还扩展到其它丰富的宏观扩散系统,例如由Fick定律描述的粒子扩散以及多物理场耦合的扩散动力学过程。这些结果为设计和实现时空调制下的非互易和拓扑扩散系统提供了新的思路和方法。
参考文献
(参考文献可上下滑动查看)
复杂科学最新论文

推荐阅读
-
从麦克斯韦妖到量子生物学,生命物质中是否潜藏着新物理学? -
困扰热力学的三个妖精 -
什么是麦克斯韦妖 | 集智百科 -
《张江·复杂科学前沿27讲》完整上线! -
成为集智VIP,解锁全站课程/读书会 -
加入集智,一起复杂!










