经济生产组织于供应链网络中,因此供应链的韧性对强劲的经济增长至关重要。各国政府均在讨论关于提高供应链韧性的政策,包括将部分供应链迁回本国,以减少对外国供应商的依赖。而根据最近发表于 PNAS 的最新研究,通过这样的政策限制买方-供应商之间的联系会减少产量,增加经济波动,同时这种经济的不稳定性也会通过网络的适应性放大。
研究领域:供应链,复杂经济学,马尔可夫链

论文题目:
Aggregate fluctuations in adaptive production networks
https://www.pnas.org/doi/10.1073/pnas.2203730119
为了抵消例如全球大流行等冲击对经济的不利影响,各国政府都在考虑减少对外国供应商的依赖程度,以提高供应链的抗冲击力,也即韧性(resilience)。
这篇文章中,作者发展并量化了一个自适应生产网络模型,来研究网络模型的韧性以及供应链回流的后果。在模型中,企业会因为外生冲击或者通过网络传播的冲击而退出,同时企业也可以替换因退出而失去的供应商,这取决于转换成本。作者将模型应用到一个大型国际公司的生产数据集,发现通过政策限制买方和供应商之间的联系,会减少产出,增加波动性(volatility),而波动性可以通过网络的适应性放大。
在经历了一系列不利的全球冲击——大流行病、半导体的持续短缺,世界已经敏锐地意识到了全球供应链的脆弱性[2]。因此,多个政府已经开始对本国关键部门的供应链进行系统性审查,以提高供应链的“韧性”。其中将供应链的部分环节迁回本国,减少对外国供应链的依赖是最主要的政策。
目前对于迁回供应链政策对缓解全球冲击的影响的早期分析,并没有显示出有系统性的好处。现有使用的模型中,外生网络模型并没有包含这样的概念:生产网络本身会在不利事件影响之后进行调整,迁回供应链也会对这些调整产生影响。进而这些模型提供的和网络韧性相关的图像是不完整的。
作者发展并量化了一个自适应网络模型,用来研究网络韧性以及迁回供应链的影响。作者考虑一大批以投入-产出为关系的企业[2]。企业的生产方式可以用一组投入和产出特征进行描述。只有当卖方的产出特征和买方的投入特征相匹配时,投入-产出的联系才会形成[3-5]。企业之间会互相配合,经历各种各样的冲击。一个企业会失去一个供应商或一个客户,这样情况下,企业可以寻找其它供应商或者客户,同时企业也会因冲击而退出市场[14-17]。这些冲击是会通过网络传播的,企业影响他的客户,导致他们的退出。
作者通过随机微分方程(SDEs)的形式对企业数量、客户分布、企业寿命分布的时间演化进行了表征。作者说明了企业的寿命是指数分布的,度分布是一个幂律分布,这两点观察结果都和数据保持一致。之后,作者使用一个大型的公司级数据集估计模型的关键参数。它包含多个生产网络之间的信息(不同行业和国家的6万家企业)。
作者主要研究的是迁回供应链对总波动率的影响,并模拟了三个大型经济体之间发生供应中断的情景(美国,东亚,欧盟),之后计算这些经济体新的总波动率。当供应链被切断时,所有三个经济体的国内网络都会进行自我重组(企业会用国内供应商取代国外供应商),显示出了自我调整的能力。冲击在这种供应网络中的传播分析与信息动力学,和社会网络中的流行病传播理论有关。有文献确定了一个阈值,低于该阈值的信息或者流行病无法广泛传播。这些阈值通常和网络的拓扑特性有关[18,19]。可是,这期间若是忽略网络的内生性,会导致结果的鲁棒性和适用性大打折扣。最后作者指出,网络中内生的自适应调整能力得到的重新布线后的结构是一种紧密连接的集群,在这种集群中,冲击是更容易传播的。虽然重新连接是来自于对失去的供应商的补充,对单个企业的生存概率产生积极的局部影响,但整体的网络拓扑结构会导致总体波动放大。
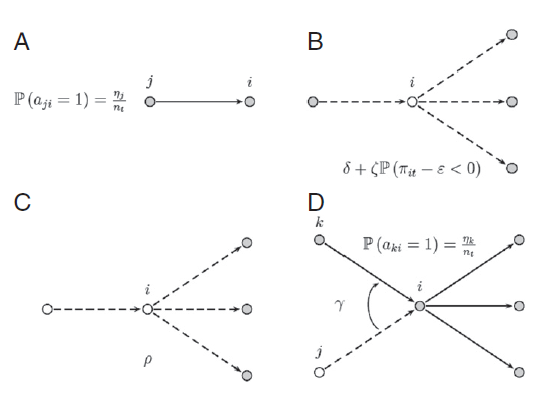
考虑一个拥有Nt个企业的经济体,每个企业用 i=1,…,Nt 来标记。时间是连续的并且用t来表示。t时刻的网络用 Gt表示。Gt 表示一类有向图,包含了Nt个企业。之后需要对企业的各种行为进行定义(作者考虑用一个时间连续的马尔可夫链来表示,初始状态G0,以下的三种事件会以相应的速率发生):
1、进入市场:当速率Ω>0时,一个新公司诞生,公司需要的原材料商品输入 l 从一个分布h(l)中采样,l∈{1,….,L},L>=1。每个输入商品的特征用p∈[0,1]的概率独立描绘,公司输出商品的特征用q∈[0,1]的概率独立描述。然后,对于每一种输入商品,只有供应商的输出特征和该输入商品的特征相匹配,才可能会成为相应的供应商。
2、退出市场:1)巨大冲击,表现为速率δ>=0,一个企业退出;2)较小的冲击,表现为速率ζ>=0,企业受到附加利润冲击,ε≥0,如果企业震后利润为负,则退出。3)冲击的扩散,表现为速率ρ>=0,失去所有供应商的公司则退出。
3、重新“布线”:如果一个企业的一个供应商退出市场,表现为速率 γ>=0,企业就会寻找一个输出特征和本企业输入特征匹配的公司来取代它。
图1:在时间演化过程中发生的不同事件的定义中引入马尔科夫链:(A)进入市场;(B)由于大或者小冲击而退出市场;(C)冲击的传播;(D)退出后更换供应商,空圆圈表示已经退出的公司。
作者从 FactSet Revere 商业关系数据库中获取有关数据集。其中包括了2003~2015年的64467家企业,有614154个环节和供应链信息。参考文献[12]也对美国经济的数据进行了分析。图2显示了2010年美国企业生产网络中最大的(弱)连接部分。网络是强烈异构的,其特征是少数节点占据网络中心位置。
图2:2010年美国企业生产网络(最大的弱连接部分)。节点的不同阴影表示不同的出度。
作者需要利用数据来估计模型中需要用到的参数,其中参考文献[39]将输入产品的特征的数量设置为300。供应商l的数量分布h(l)可以从经验分布中得到,同样,从观察到的企业出口,可以通过生存模型[40]估计退出率δ,ζ以及ρ。从数据中企业替换供应商的事件中,可以估计重新布线的概率γ。其余的参数可以通过匹配数据和模型各自的有关企业的生存期和脱离度的总分布来获得(具体细节可以参考原文公式8和9)。
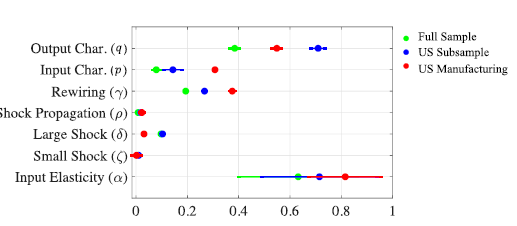
图3:对不同的数据样本进行参数估计:分别是:输入韧性(α),小冲击(ζ),大冲击(δ),冲击传播(ρ),重新布线(γ),输入特性(p)和输出特性(q)。参数估计过程在原文的方法部分进行了详细说明,其中α通过公式15估计,ζ,δ,ρ通过最大似然估计,见公式18,γ是公式19最大似然估计得来,p,q通过公式20,使用马尔可夫链蒙特卡洛-伪最大似然估计(MCMC-PMLE)算法得到。
从图3的结果可以看出,三种数据集的参数估计在统计上都是有显著性差异的,唯一例外的例子是小冲击参数ζ的估计,在整个样本中并不显著,但在考虑的子样本中显著且大小相似。
估计了模型参数之后,我们现在就能够通过模型来评估不同政策干预影响的情景(并非真实情况)。比如作者考虑了一个反事实的情景,即美国国内、欧盟、东亚(中国、日本、韩国、香港、新加坡)各自只有国内的买方-供应商的关系。受到影响的买方-供应商关系如图4。
图4:美国(红色)和非美国,欧盟(绿色)和非欧盟,东亚(蓝色)和非东亚的买方-供应商关系,公司的位置用圈表示。
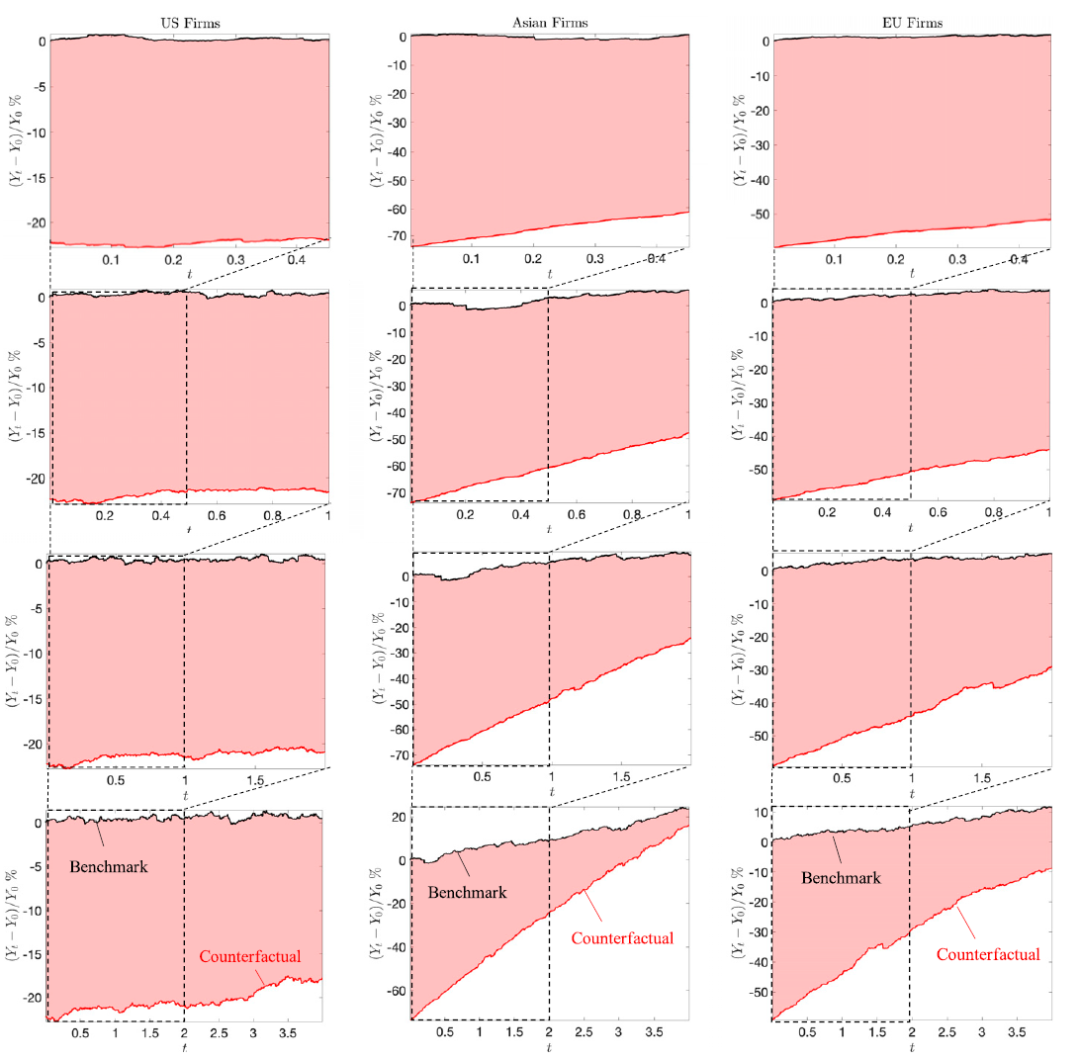
图5显示了美国、欧洲、东亚企业总产出相对变化的脉冲响应函数(和各自基准相比)。同时上述模拟的反事实的情况随着时间演化也可视化在图中,可见反事实的模拟情况:迁回供应链的影响是巨大的,美国短期产出损失了22%,欧盟占60%,亚洲占70%,所有国家都要经历长期复苏才能达到基准的产出水平。
图5:美国、欧盟和东亚在不同的时间范围内的总产出相对变化的脉冲响应函数
作者提出的网络模型,让我们能够在自适应网络中分析政策干预对总产出的影响。作者的研究表明,通过迁回供应链限制买方-供应商之间的关系会减少产出并增加波动性。此外,作者还向我们表明,更强的网络自适应性并不一定使其更稳定,相反,极有可能会放大整体的波动性。最后,在具有合适数据集的情况下,气候、流行病等因素的影响也可以纳入到模型中。
[1] A.W. Bartik et al., The impact of COVID-19 on small business outcomes and expectations. Proc. Natl. Acad. Sci. U.S.A. 117, 17656–17666 (2020).
[2] J. McNerney, C. Savoie, F. Caravelli, V. M. Carvalho, J. D. Farmer, How production networks amplify economic growth. Proc. Natl. Acad. Sci. U.S.A. 119, e2106031118 (2022).
[3] C. A. Hidalgo, R. Hausmann, The building blocks of economic complexity.Proc. Natl. Acad. Sci. U.S.A. 106, 10570–10575 (2009).
[4] R. Hausmann, C. Hidalgo, The network structure of economic output. J. Econ. Growth 16, 309–342(2011).
[5] K. A. Anderson, Skill networks and measures of complex human capital. Proc. Natl. Acad. Sci. U.S.A. 114, 12720–12724 (2017).
[6] D. Acemoglu, V. Carvalho, A. Ozdaglar, A. Tahbaz-Salehi, The network origins of aggregate fluctuations. Econometrica 80, 1977–2016 (2012).
[7] V. Carvalho, Aggregate fluctuations and the network structure of intersectoral trade. University of Pompeu Fabra Working Paper 1 (2009). https://ideas.repec.org/p/upf/upfgen/1206.html. Accessed 20 August 2022.
[8] E. Atalay, A. Hortac¸su, J. Roberts, C. Syverson, Network structure of production. Proc. Natl. Acad. Sci. U.S.A. 108, 5199–5202 (2011).
[9] E. Oberfield, A theory of input–output architecture. Econometrica 86, 559–589 (2018).
[10] K. Lim, Firm to firm trade in sticky production networks. Mimeo, Princeton University (2016). https://ideas.repec.org/p/red/sed017/280.html. Accessed 29 August 2022.
[11] D. Acemoglu, P. D. Azar, Endogenous production networks. Econometrica 88, 33–82 (2020).
[12] M. Taschereau-Dumouchel, Cascades and fluctuations in an economy with an endogenous production network.Mimeo, Cornell University (2017). https://ideas.repec.org/p/red/sed017/700.html. Accessed 29 August 2022.
[13] M. Elliott, B. Golub,M. V. Leduc, Supply network formation and fragility. Am. Econ. Rev. 112, 2701–47 (2022).
[14] C. Moore, G. Ghoshal, M. E. Newman, Exact solutions for models of evolving networks with addition and deletion of nodes. Phys. Rev. E Stat. Nonlin. SoftMatter Phys. 74, 036121 (2006).
[15] B. Karrer, G. Ghoshal, Preservation of network degree distributions from non-uniform failures. Eur. Phys. J. B 62, 239–245 (2008).
[16] J. S. Kong, N. Sarshar, V. P. Roychowdhury, Experience versus talent shapes the structure of the Web. Proc. Natl. Acad. Sci. U.S.A. 105, 13724–13729 (2008).
[17] J. Saldan˜ a, Continuum formalism for modeling growing networks with deletion of nodes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 75, 027102 (2007).
[18] A. Montanari, A. Saberi, The spread of innovations in social networks.Proc. Natl.Acad. Sci. U.S.A. 107, 20196–20201 (2010).
[19] T. Rogers, Assessing node risk and vulnerability in epidemics on networks. Europhys. Lett. 109, 28005 (2015).
[20] T. Gross, C. J. D. D’Lima, B. Blasius, Epidemic dynamics on an adaptive network. Phys. Rev. Lett. 96,208701 (2006).
[21] J. Grilli, T. Rogers, S. Allesina,Modularity and stability in ecological communities. Nat. Commun. 7,12031 (2016).
[22] T. F. Bresnahan,M. Trajtenberg, General purpose technologies “engines of growth?” J. Econom. 65, 83–108 (1995).
[23] E. Helpman, General Purpose Technologies and Economic Growth (The MIT Press, 1998).
[24] D. Acemoglu, A. Ozdaglar, A. Tahbaz-Salehi, Systemic risk and stability in financial networks. Am. Econ. Rev. 105, 564–608 (2015).
[25] D. S. Evans, The relationship between firm growth, size, and age: Estimates for 100 manufacturing industries. J. Ind. Econ. 35, 567–581 (1987).
[26] T. Klette, S. Kortum, Innovating firms and aggregate innovation. J. Polit. Econ. 112, 986–1018(2004).
[27] G. A. Calvo, Staggered prices in a utility-maximizing framework. J. Monet. Econ. 12, 383–398 (1983).
[28] M. O. Jackson, B.W. Rogers,Meeting strangers and friends of friends: How random are social networks? Am. Econ. Rev. 97, 890–915 (2007).
[29] R. Pastor-Satorras, A. Vespignani, Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203 (2001).
[30] M. Jackson, B. Rogers, Relating network structure to diffusion properties through stochastic dominance. B.E. J. Theor. Econ. 7, 1–13 (2007).
[31] Y. Moreno, R. Pastor-Satorras, A. Vespignani, Epidemic outbreaks in complex heterogeneous networks. Eur. Phys. J. B Cond. Matter Complex Syst. 26, 521–529 (2002).
[32] M. Barthelemy, A. Barrat, R. Pastor-Satorras, A. Vespignani, Velocity and hierarchical spread of epidemic outbreaks in scale-free networks. Phys. Rev. Lett. 92, 178701 (2004).
[33] J. Gomez-Gardenes, V. Latora, Y.Moreno, E. Profumo, Spreading of sexually transmitted diseases in heterosexual populations. Proc. Natl. Acad. Sci. U.S.A. 105, 1399–1404 (2008).
[34] D. Stroock, An Introduction to Markov Processes (Springer Verlag, 2005), vol. 230.
[35] S. Elaydi, An Introduction to Difference Equations (Springer, 2005).
[36] A. Coad, The exponential age distribution and the Pareto firm size distribution. J. Ind. Compet. Trade 10, 389–395 (2010).
[37] S. Chava, A. Purnanandam, Is default risk negatively related to stock returns? Rev. Financ. Stud. 23, 2523–2559 (2010).
[38] S. Chava, R. A. Jarrow, Bankruptcy prediction with industry effects. Rev. Finance 8, 537–569 (2004).
[39] G. Hoberg, G. Phillips, Text-based network industries and endogenous product differentiation. J. Polit. Econ. 124, 1423–1465 (2016).
[40] A. Cameron, P. Trivedi, Microeconometrics: Methods and Applications (Cambridge University Press, 2005).
[41] C. J. Geyer, Markov Chain Monte Carlo Maximum Likelihood (Interface Foundation of North America, 1991).
[42] R. C. Lewontin, On the measurement of relative variability. Syst. Zool. 15, 141–142 (1966).
[43] K. Huremovic, F. Vega-Redondo, Production networks. Bocconi University Working Paper (2016). https://ideas.repec.org/p/aim/wpaimx/1633.html. Accessed 29 August 2022.
[44] R. E. Lucas, On the size distribution of business firms. Bell J. Econ. 9, 508–523 (1978).
[45] L. Katz, A new status index derived from sociometric analysis. Psychometrika 18, 39–43 (1953).
[46] P. Bonacich, Power and centrality: A family of measures. Am. J. Sociol. 92, 1170–1182 (1987).
[47] T. Kurtz, Limit theorems for sequences of jump Markov processes approximating ordinary differential processes. J. Appl. Probab. 8, 344–356 (1971).
[48] G. Guo, Event-history analysis for left-truncated data. Sociol.Methodol. 23, 217–243 (1993).
[49] A. Kolotilin, V. Panchenko, Estimation of a scale-free network formation model. MIT Working Paper(2018). https://ideas.repec.org/p/swe/wpaper/2018-10.html. Accessed 29 August 2022.
[50] M. Koenig, Replication Data for “Aggregate fluctuations in adaptive production networks.” Harvard Dataverse. https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/2PW9DN. Deposited 26 August 2022.
经济学理论的发展与社会环境变化密切相关。一方面,伴随计算机的发展,相应的研究技术日渐成熟,例如非线性动力学、复杂网络、ABM等,为研究者提供了更强大的分析工具;另一个方面,对“均衡”的经济学的研究,不能够解释实际的经济现象,例如金融危机、创新产生的新的发展模式等,研究者开始重视经济学的“非均衡”现象,把经济系统看做复杂系统,并力图做出更能反映现实的研究。经济学内慢慢出现了一种基于更加现实的假设的研究进路,复杂经济学一个新的经济学框架正在形成。为了促进此领域的交流与合作,我们发起了复杂经济学读书会。
复杂经济学读书会第二季由北京师范大学李红刚、王有贵、张江、陈清华老师以及中山大学袁先智老师联合发起,从7月11日起每周一 19:00-21:00 进行,预计持续 10-12 周。我们将围绕复杂经济学的内涵、基本方法、普适规律、应用场景四个方面进行探讨,并计划组织三次圆桌讨论,与国内外学者进行深入探讨。热诚欢迎对复杂系统研究和经济学感兴趣的学生和学者加入这个读书会,一起探索和探讨经济复杂系统的真谛!