集智复杂系统NetLogo建模竞赛是由集智俱乐部发起、面向广大社会公众的复杂系统建模竞赛。比赛旨在普及复杂系统相关知识、推广NetLogo的应用及为学生学者们提供一个学术交流展示的机会。赛事主要考查复杂系统领域问题的抽象与建模、计算机编程与分析能力,并对优胜组给予课程资源、教授指导等激励。
本次集智复杂系统NetLogo建模竞赛在2022年8月-10月期间展开,共设置三个赛题。比赛期间,二十余参赛小组借助NetLogo对赛题进行了精彩而细致的研究。三位老师也为赛事设计了精彩的题目以及点评。
赛题一命题老师、评委老师 胡乔
胡乔,毕业于东南大学,集智学园算法工程师。主要工作和研究方向为复杂系统相关的文献挖掘、科学学和知识库构建,对基于多主体模拟的复杂系统建模也有持续的研究兴趣,曾参与多个相关科研项目和课程的开发,也是集智NetLogo社群的组织者之一。
赛题二出题老师、评委老师 高济禾
高济禾,多 agent 建模专家,十余年 NetLogo 开发经验,曾自制国内最早一批 NetLogo 在线培训容,曾与多个科研团队合作开展 ABM 与 NetLogo 建模培训与课题研究,涉及公共管理、生命科学、金融市场、城市与交通等多个领域,具有丰富的 NetLogo 培训经验。目前在北航可靠性研究所任仿真工程师,曾任北京博晓通科技分析团队负责人、宣亚国际传播集团策略顾问。本 业于南京大学天文学系、硕士毕业于华东师范大学物理系。部分工作见Github:https://github.com/jihegao/
赛题三出题老师、评委老师 高德华
高德华,山东工商学院副教授,管理学博士,硕士生导师。长期致力于运用复杂系统仿真模拟和计算方法来分析研究社会经济与组织管理中的重大热点问题,科研兴趣包括复杂管理系统仿真及优化、计算社会学与计算组织科学、工业系统工程等,以第一/通讯作者在《Review of Managerial Science》、《Computational and Mathematical Organization Theory》、《Journal of Artificial Societies and Social Simulation》等国内外学术期刊和会议上发表论文20余篇,出版学术著作1部。
评委老师 卢燚
卢燚,西安交通大学应用数学博士,现为大学讲师,曾在华为工作三年,拥有多年编程实战经验和一线教学经验,熟练掌握Python和NetLogo语言,对函数式编程有着浓厚的兴趣。讲授爬虫课两年,积累了大量的案例。
在比赛中,选择探索朗顿的蚂蚁赛题的小组对这一经典问题从改变角度、改变颜色等多个富有创意的角度进行探索;选择无人机集群赛题的小组多为相关领域出身,凭借丰富的专业知识对这一赛题进行了深入的研究;选择居住隔离赛题的小组们在研究这一课题时更加注重这一情景在现实中的意义,综合应用了不同学科的思维。
最终,邱仲普小组、刘雷小组、申政小组分别获得三个赛题的一等奖,在此,组委会邀请他们对自己的研究成果与参赛感想进行分享。
邱仲普 北京师范大学系统科学学院 系统理论专业研究生
马奥 北京师范大学系统科学学院 系统分析与集成专业研究生
徐茂深 北京师范大学系统科学学院 系统分析与集成专业研究生
朗顿的蚂蚁(Langton’s ant)是人工生命领域一个著名的模型。作为一种二维格点上的元胞自动机,它由人工生命之父Christopher Langton在1986年给出[1],并被证明图灵完备的 [2]。
它的规则非常简单:
– 一只蚂蚁被放置在拥有两种状态(黑与白)的正方格点(lattice)上;
– 若蚂蚁在白格,右转90度,将该格改为黑格,向前移一步;
– 若蚂蚁在黑格,左转90度,将该格改为白格,向前移一步。
但由于主体和环境之间存在着非线性的相互作用,这个模型的演化和涌现行为却非常复杂:蚂蚁的轨迹会演化出两种模式:(chaotic pattern)混乱模式和周期性规则模式(regular periodic pattern),后者被称为“高速公路”(highway)[3]。虽然没有被证明,但对于所有的已知初始条件,蚂蚁总是从无序(disorder)的前者转变为有序(order)的后者,即一种无限延续的相(a propagation phase)[4]。这可以被视为一种相变。
不同的初值条件(或者称为初始构型,configuration)会在不同的步长(称为相变时间)发生相变,而且初值条件的哪怕轻微改变都会导致相变时间的巨大变化。对于最简单的全黑构型,相变时间大概在10000步左右。而只需将(0,1)格涂白,就可以将相变时间降低到3000步左右。这种初值敏感性表明这个模型的时空上的动力学混沌性[5]。
文献[5]试图通过调节初值条件以最大化相变时间,但作者坦诚地承认,这个混沌系统无法被合理调节,最佳初值条件方面似乎也没有规律性(this chaotic system is not reasonably controllable and appears to have no regularity in the “optimal” initial conditions.)
我们的小组研究的优化方向正好与上述文献相反。我们试图回答的问题是:怎样的初值条件可以最小化相变时间?相变时间能否减少为0(即一开始就进入highway状态)?如果可以,那么怎样寻找相变时间为零且初始构象更简单的条件呢?
netlogo是针对多主体建模(Multi-agent modeling)的专业软件,它独特的语法使得本模型的代码实现是非常容易的。但问题的困难之处首先在于如何捕捉到系统的有序(order)——蚂蚁怎样才算进入了高速公路的修筑状态?
通过查阅文献[3]和简单计算,我们意识到蚂蚁在有序相产生的周期性规则模式,是以104步为时间周期,以为空间周期的,即,每104步蚂蚁会在水平和垂直方向上各移动2格。
明确了这一点,我们在netlogo的程序设计上,通过判断蚂蚁的运动是否持续满足时空周期性条件,就能判断蚂蚁是否进入了有序相。
其次,这个问题的另一艰巨性在于:使用穷举法会导致巨大到不现实的计算成本——若考虑哪怕这样简单的格点规模,都会导致个构型需要被研究;但系统的动力学混沌性又导致传统的梯度下降类的优化算法无法发挥其有效性。
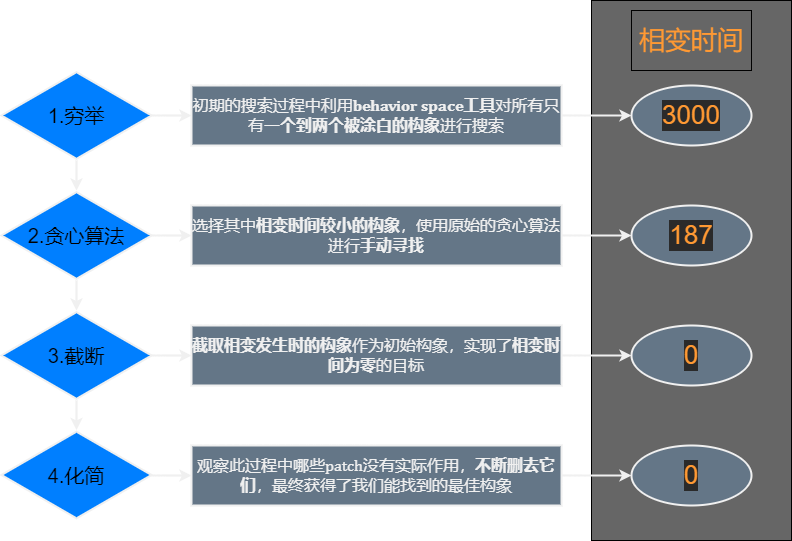
为了解决这一问题,我们的算法综合采用了多种方法。在白色格点数量很少时,对构型进行穷举;继而在数量较大时,则采取贪心算法,对构型进行持续优化;而当贪心算法收敛到某个局部最小值时,我们则采用截断-删除法,确保相变时间为零的同时,实现对局部最小构型的删减,最终得到了结果。
我们在初期的搜索过程中利用behavior space工具对所有只有一个到两个被涂白的构型进行搜索;
继而选择其中相变时间较小的构型,使用原始的贪心算法进行手动寻找,将相变时间提前到200以内;如图:
在此基础上,我们估计了初始构型的复杂程度,转换思路,在之前的工作的基础上,截取相变发生时的构型作为初始构型,实现了相变时间为零的目标
观察此过程中哪些patch没有实际作用,并不断删去它们,最终获得了我们能找到的最佳构型。以此 如图:仅有14个patch被涂白了
此模型有一个重要而未得到解决的问题:是否任意构型都会发生相变?我们对此进行了文献调研,并给出了我们的猜想。
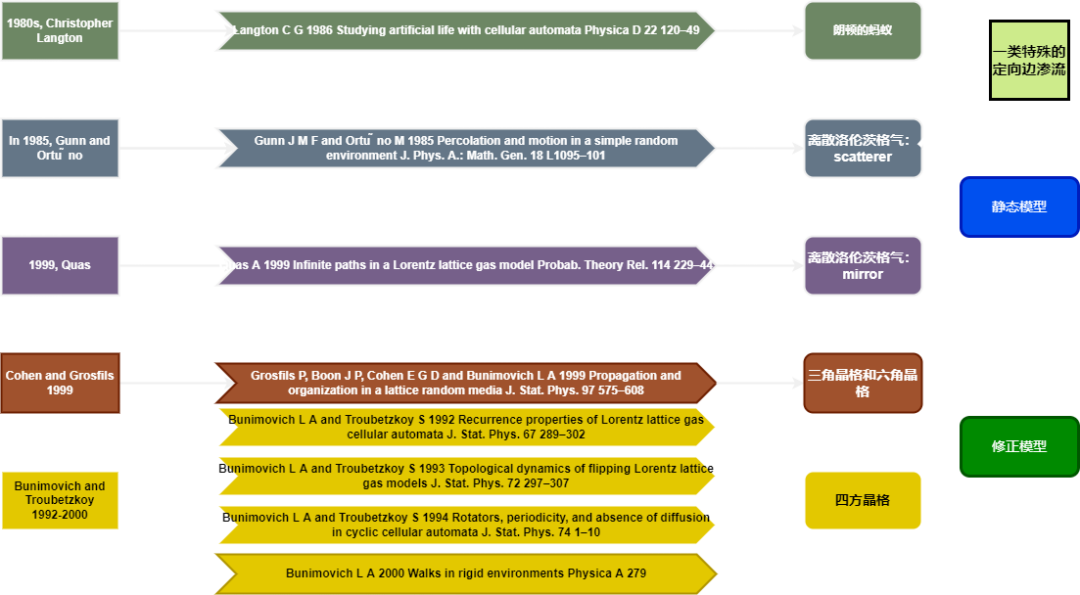
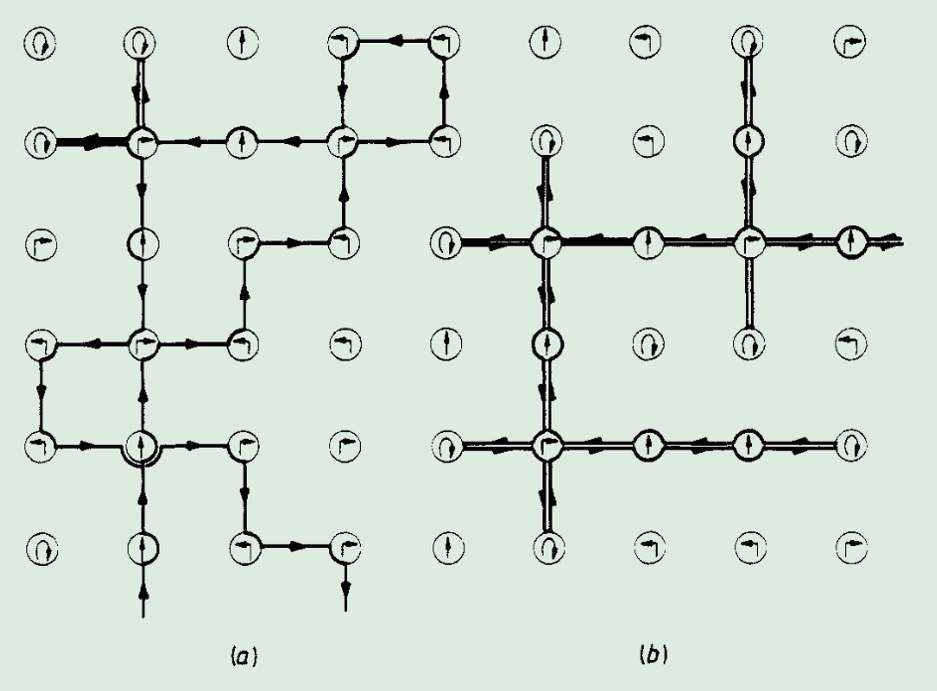
其实除了Langton在1980年代的研究[1],在物理和随机行走领域,具有相同本质的模型也得到了发展。1985年Gunn和Ortuno定义了一个离散版本的洛伦兹格气模型(Lorentz’s gas model):二维格子上的每个格点放置了一个转向器(scatterer)的运动,它可以以特定角度改变粒子的速度方向。这个模型可以被视为一种特殊的边渗流问题。如图是两种典型的情况。
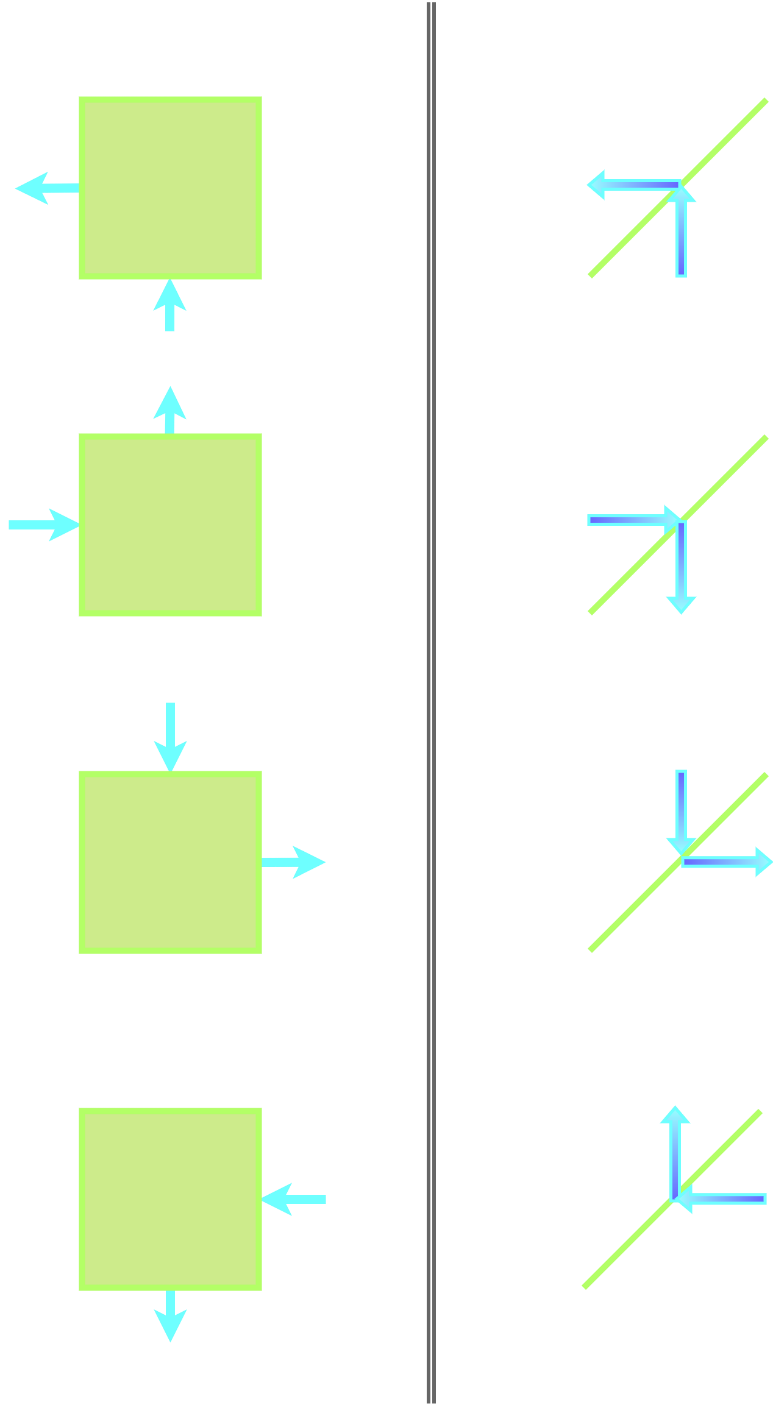
在最初的例子里,转向器是四向的(即粒子速度的方向可以被改变0度、90度、180度或者270度)。这对应于有四种而非两种颜色的朗顿蚂蚁。相应地,二向转换器对应于二色的朗顿蚂蚁,只是蚂蚁失去了涂色能力。
而在1999年,Quas的工作里,转向器被设定为镜式(mirror-like)的。此时模型其实等价于光束在等间距的双面镜集群之间反射。
图表 [1]如图是二向转向器和镜式转向器(mirror-like scatterer)的规则对比
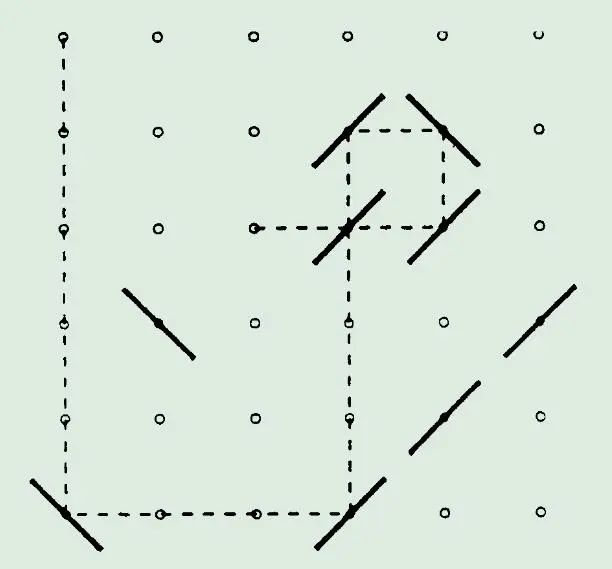
图表 [2]如图是一个典型的镜式转向器条件下的构型
这一类模型被称为静态模型(static models),因为环境本身并不会因为粒子的运动而改变。
而与之相对的是Cohen在Gunn模型基础上发展而来的修正模型:在之前模型的基础上,粒子被赋予了一种翻转(flip)转向器的能力。即粒子在经过转向器,可以将转换器从一种状态转变为另一状态。这会使得环境与粒子之间的耦合变得高度非线形。
Cohen考虑了三角格点和六角格点,而Bunimovich和Troubetzkoy关注于正方格点,他们证明了蚂蚁轨迹的无界性[4][7][8]。但是否任意初始构型下,蚂蚁都会修建高速公路依旧是一个开放问题。
考虑到:
1. 静态模型与渗流理论的对应
2. 静态模型中,左右转向器比例(作为序参量)的变化可以导致粒子轨迹的局域-离域相变。是否超过临界阈值决定了系统的行为。
我们猜测,朗顿蚂蚁模型存在某种特殊的临界阈值为零的渗流相变,由于临界条件总是被满足,所以任意初始构型都会产生高速公路的修筑。
邱仲普,北京师范大学系统科学学院系统理论专业博士生,导师为樊京芳老师。本科就读于四川大学物理学拔尖班。主要从事相变与临界现象,地球系统复杂性研究。
马奥,在河南财经政法大学取得学士学位,目前就读于北京师范大学系统科学学院,导师为陈育涵老师,主要研究兴趣为计算神经科学方向。
徐茂深,在东北大学(秦皇岛)取得学士学位,目前是北京师范大学系统科学学院硕士研究生,导师为斯白露教授,主要研究兴趣是人工神经网络的解释,以及神经动力学和神经流形。
另外,感谢武汉科技大学的王薏潮同学和北京师范大学的郑孙婧同学,他们作为团队成员参与了无人机方向的比赛,并为本研究提供了帮助。
[1] LANGTON C G. Studying Artificial Life with Cellular Automata[J/OL]. Physica D: Nonlinear Phenomena, 1986, 22(1): 120-149. DOI:10.1016/0167-2789(86)90237-X.
[2] GAJARDO A. MOREIRA A. GOLES E. Complexity of Langton’s Ant[J/OL]. Discrete Applied Mathematics, 2002, 117(1): 41-50. DOI:10.1016/S0166-218X(00)00334-6.
[3] BOON J P. How Fast Does Langton’s Ant Move?[J/OL]. Journal of Statistical Physics, 2001, 102(1): 355-360. DOI:10.1023/A:1026581213671.
[4] BUNIMOVICH L. TROUBETZKOY S. Recurrence Properties of Lorentz Lattice Gas Cellular Automata[J/OL]. 1992. DOI:10.1007/BF01049035.
[5] I I D L. POSPÍCHAL J. How Random Is Spatiotemporal Chaos of Langton’s Ant?[J/OL]. Journal of Applied Mathematics, Statistics and Informatics, 2015, 11(2): 5-13. DOI:10.1515/jamsi-2015-0008.
[6] GROSFILS P. BOON J P. COHEN E G D. 等. Propagation and Organization in Lattice Random Media[J/OL]. Journal of Statistical Physics, 1999, 97(3): 575-608. DOI:10.1023/A:1004611208149.
[7] BUNIMOVICH L A. TROUBETZKOY S E. Topological Dynamics of Flipping Lorentz Lattice Gas Models[J/OL]. Journal of Statistical Physics, 1993, 72(1): 297-307. DOI:10.1007/BF01048051.
[8] BUNIMOVICH L A. Walks in Rigid Environments[J/OL]. Physica A: Statistical Mechanics and Its Applications, 2000, 279(1): 169-179. DOI:10.1016/S0378-4371(99)00518-X.
刘雷 中国兵器工业集团航空弹药研究院有限公司 主管设计师
于子钧 中国兵器工业集团航空弹药研究院有限公司 主管设计师
叶得濠 中国兵器工业集团航空弹药研究院有限公司 主管设计师
集群化、自主化、智能化的无人机集群是未来无人机的重要发展方向。而无人机之间的目标分配、编队、避障等问题,逐渐在无人机飞控策略中占据较为重要的地位,为了研究这些问题,探索合适的策略,我们计划使用NetLogo语言来抽象不同无人机行为,观察不同的策略之间的区别,确定下一步的研究方向。
为了解决这些问题,我们尝试引入了“指挥官”和“打击者”的角色设置,将第一个发现敌方的无人机设置为“指挥官”,并要求“指挥官”能够将周围部分没有目标的无人机变为“打击者”,并和自身一起组成小队,共同打击一个目标。并通过“指挥官”角色之间的信息交互,确保他们能够选定不同的目标,避免浪费无人机。
继续观察代码运行情况,发现同一小队飞往目标时往往会变得较为密集,尤其在进入敌方打击范围之后,更加密集的小队会使得在敌人的一次打击中更难存活。因此,我们效仿模型库中的 Flock 模型对分散策略进行了改进,使每个编队都能在敌方范围内保持分散状态,使一个敌人的一次攻击只能消灭一架无人机。但在后续的进一步试验中,我们发现Flock 模型的分散方法效果不是很显著,于是采用了距离矢量加和的方式解得无人机的疏散方向:即对于任意一架无人机A,将距离A小于敌方攻击爆炸半径距离内的所有无人机到A作距离矢量,将这些距离矢量加和后,可以得出无人机A疏散的方向。
优化了目标分配策略,我们发现在Ver1.0版本中的策略不会动态的改变无人机的角色,于是加入了当目标被消除后,重置无人机小队中所有存活的无人机的角色,使它们能够继续参与下一轮攻击,达到最大效率。为了减少无人机向目标飞行时间,我们对无人机小队进行了扩充,让每个“指挥官”拉取4个距离自己最近的无目标无人机和3个距离最远的无目标无人机,使得整个集群向前推进,节约了集群分裂后,后方集群重新飞向目标的时间。
优化了分散策略,在Ver1.1 版本中,有部分处在世界边缘的无人机会因为策略原因被挤出世界(abs xycor>16),被挤出世界后,方向在世界外的无人机会停留在原地,于是我们添加了世界边缘检测返航机制,在无人机达到世界边缘后,自动机头方向,飞向世界中心位置(0 0)
我们发现敌方单位生成位置对于任务完成时间有相当大的影响,左右两侧的敌方数量差距、敌方单位的疏密程度都会使得完成时间有变化。因此我们将无人机按照其位置分为三组,分别为40、20、40,使用list来存储感知范围内的敌方单位。其中左、右两个集群负责打击,中间集群通过list中左、右两侧地方数量的对比,向两个集群添加、或减少无人机数量。
在本次研究中,对首要目标(完成任务所需时间)的把控较为出色,但一定程度上忽略了存活率、弹药利用率等次要目标,希望能在后续研究中继续改进策略。1NetLogo 作为一门建模语言,通过并行的模拟多个个体单位的行为,来展示出宏观的“涌现”现象,进而解决目标任务,为无人机决策研究提供了一个新的思路。
作为这次参赛最“特殊”的一个小组,我给我们小组打的标签是“入门菜鸟”、“班门弄斧”。简单介绍一下小组成员,申政、吴丹、成伊萌,我们来自中南大学公共管理学院2022级MPA专业,作为三名研一的非全MPA研究生,我们在这个领域是刚入门的“菜鸟”。
而与netlogo的结缘,源自对吕鹏教授《社会计算科学》在线课程的学习,吕鹏教授细致的讲解为我们打开了学科的大门,而个体行为对群体的影响、微观到宏观的因果涌现、“简陋”但严谨的语言特性,这些netlogo的魅力之处让我们深深着迷。我们也研读了吕鹏教授的多篇论文,尝试着用netlogo去实现论文中的研究方法。
总的来说,在参赛之前我们还是三只只有两个月经验的“入门菜鸟”,但是在看到公众号推送的竞赛消息时,不知是哪里来的一股“初生牛犊不怕虎”的勇气,我们决定“班门弄斧”,“重在参与”一次,尝试完成一下赛题。
动手前,我们仔细阅读了三道赛题,对赛题的难度有个初步判断。
赛题一朗顿的蚂蚁,模型规则很简单,但是在搜索引擎搜寻了一番后,发现互联网上对这个模型的现象介绍较多,但对原理有探究讲解者寥寥,对新手不太友好;赛题二无人机集群,需要一定的寻路、集群、强化学习的算法基础,可能还需要引入外部python程序,难度偏大;而赛题三居住隔离模型,赛题提出的研究点难度适中,符合我们团队的能力水平,特别是研究点一提出的异质性影响,与之前阅读过吕鹏教授的一篇研究个体异质性对网络谣言传播S曲线影响论文的研究内容十分相似,可以作为我们小组研究的突破点。
研究过程
在确定赛题后,接下来我们的主要工作是:
一、 阅读原模型源码,弄清原模型的交互逻辑和规则;
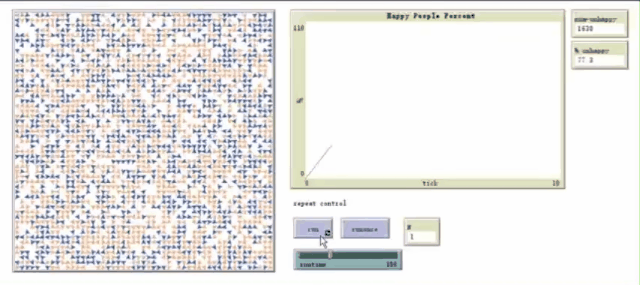
二、 查找、阅读文献。尤其是对吕鹏教授《Exploring S-shape curves and heterogeneity effects of rumor spreading in online collective actions》一文的重点研读,借鉴了其利用random-normal函数实现个体异质性的方法,并将其观察谣言传播率S曲线的方法拓展到本研究中对人群满意度变化S曲线上,多次模拟的S曲线变化如图;
三、 确定研究点四创新思考方向,在查找文献过程中我们发现有学者关注到70年代美国的土地政策,我们觉得这个是一个很有意思的结合netlogo模型的研究方向,于是将其作为研究点四的创新思考;
四、 编写代码,实现研究点;
五、 设置实验对照组,提出实验假设;
六、 进行实验模拟,验证假设;
在完成这一次研究后,我们对自己工作存在的不足也十分清楚:
首先,研究局限于对实验现象的模拟,未做任何的定量分析,得出的结论缺少有力的支撑,后续会补充这一方面的学习;
其次,研究内容还比较初级,高老师的评价十分中肯:“小组的工作量还是足够,但是研究还比较浅显,比如对美国土地政策的研究可以结合收入水平等多种因素进行模拟,尤其是作为公共管理的学生这应该是你们擅长的研究方向”;
最后,我们对netlogo语言的运用还不熟悉,比如高老师提到的行为空间,我们还没有使用过,代码编写过程中花了大量的时间在查找语法上,所完成的代码运行效率也不高,运行很慢,这也是后续可以继续优化的方向。
十分感谢集智学园提供的这次宝贵的比赛机会,也非常感谢各种专家老师的指导,在旁听其他参赛组介绍时,我们也学习到了很多新的研究方法和思路,有很多启发。漫漫研究路,我们只是刚入门的研一菜鸟,向大家多多学习。
本次集智复杂系统NetLogo建模竞赛到此已圆满结束,恭喜所有获奖小组,也感谢所有小组的参与与支持。