深入理解社会经济系统背后的复杂性,一直是社会科学的研究重点,但直到复杂性科学(Complexity Sciences,或译复杂科学)作为一门学科出现之前,这一探索道路始终崎岖艰难。作为密歇根大学复杂系统研究中心负责人,同时也是计算社会科学家的Scott E. Page教授,撰写了本篇综述,梳理了复杂性科学(complexity sciences)为社会科学研究提供的重要方法、工具和思路。本文讨论了复杂性的概念、正在蓬勃发展的复杂系统研究领域以及该领域与社会学的关系。首先,通过比较众多复杂性的定义之异同,本文描述了能够产生复杂性的系统特征:多样性 (diversity)、网络化的互动结构 (networked interactions)、相互依赖的行为 (interdependent behavior) 以及适应(adaptation)。接着,本文梳理了与社会学最有共鸣的复杂性科学研究成果。本文将这些成果分为四种类别:动力学 (dynamics)、聚集 (aggregation)、分布 (distributions) 以及结构和多样性的功能属性(functional properties of structure and diversity)。在此基础上,本文认为将复杂性科学纳入社会学需要引入新的模型和方法,以及探索更加广阔的实证研究路径,而更深入地吸收复杂性也将对社会学大有裨益。
Scott E. Page | 作者
单俊杰 | 译者
刘培源 | 审校
邓一雪 | 编辑

论文题目:
What Sociologists Should Know About Complexity
https://www.annualreviews.org/doi/abs/10.1146/annurev-soc-073014-112230
1. 导论
2. 复杂性和复杂适应性系统
3. 图解涌现
4. 动力学
5. 聚集
6. 分布
7. 多样性和结构
8. 讨论
在这篇文章中,我描述了一系列的想法、模型、结果、理论和技术,它们都被松散地归入复杂性科学的标签下。同时,我还讨论了它们与社会学的关系以及对社会学的潜在影响。复杂性科学这门学科在学术期刊和大众媒体上都引起了极大的关注,部分原因在于世界的复杂性不断增加,原因还在于高维数据的大量出现。复杂性科学的倡导者们认为,复杂系统的方法扩大了我们可以考虑的问题范围、我们可以收集和使用的数据类型、以及我们可以识别和分析的现象类别。他们还认为从复杂性的角度出发,我们必须重新考虑与世界如何运作以及系统如何聚合这些问题所紧密关联而又习以为常的假设和观念。
一些学者将复杂性科学视作一种具有变革意义的“新科学”,这种“新科学”将会改变当前的科学实践 (Wolfram 2002) 。而我则持有一种更为温和的主张,复杂性科学聚焦于许多曾经无人问津的问题,因而有希望作为当前社会科学研究方法的补充。复杂性科学的方法代表了社会科学方法论上的另一只箭 (Castellani & Hafferty 2009) ,这支箭可以帮助改善社会科学研究以及指导和设定政策选择 (Colander & Kupers 2014) 。
为了明确目标,我对复杂系统研究中具有社会学意义的方法、发现、概念和模型进行了个人化(而且有点特立独行)的介绍。在这一过程中,我有选择地评论了一些已发表的社会学研究,但我并没有试图对社会学和复杂性研究的交集进行全面的文献回顾。这意味着我忽略了社会学中一些优秀的复杂性研究的例子。因此,我要求把这篇文章看作是对一系列想法的回顾,而不是更为传统的文献回顾。
复杂性与社会学的关联始于一种共鸣。正如我作为局外人看到的那样,社会学这门学科试图合理化个人与个人的集合体——群体、阶级和社会——之间的互动,并探索这些互动是如何为人类心理、文化、社会结构和正式组织所形塑。简而言之,社会学认为主体(agents)身处于网络、群类和地域等环境之中。与经济学不同,在社会学中,这些环境或场域发挥着核心作用(Bourdieu 1984, 1993)。
社会学拥抱变化和进步,而不假定均衡状态的存在。从社会学的角度来看,我们的社会、经济和政治生活都是动态的——允许有新的想法、群类和技术。这些创新可以产生复杂的(非稳定的)动力学。最后,社会学的一些部分研究接受了这样一种可能性,即一个群体可以有独立于其成员而存在的涌现性质(Byrne & Callaghan 2014, Little 2012, Sawyer 2005)。
在社会学中,许多缜密的思想和信念在复杂系统中占据了核心地位(Xie 2007)。简而言之,复杂系统由嵌入的、适应的、多样的个体构成,这些个体之间的互动产生了更高阶的结构(自组织)和功能(涌现)。复杂性科学的研究者和社会学家们一样,为这些系统的性质所吸引。这些系统是稳健的吗?行为如何聚集?形成了什么结构?涌现出了什么样的模式?出现了哪些跨类型的分布?系统中的实体是持续的吗?这些系统会随着时间变得更加复杂吗?目前为止,我们对复杂系统所拥有的认识令人印象深刻但又失之片面。我们知道,复杂系统往往是不可预测的,很难描述和定义,往往容易收到大事件的影响,而且容易产生跨类别的长尾分布 (Miller & Page 2007, Mitchell 2009) 。
我可以有把握地宣称(使用维恩图术语),社会学中一个有意义的部分与复杂性科学的一个重要子集相重合。也就是说,尽管社会学家研究的大部分内容可以被认为是发生在一个复杂系统中,但并不是所有都是如此。换言之,尽管复杂系统包括社会学关注的问题,但复杂系统研究中的许多内容与社会学没有什么关系。例如,一些复杂系统科学家研究是对社会学不太重要的社会行动,如交通模式(Nagel & Paczuski 1995)、金融崩溃(Goldin & Mariathasan 2014)以及国际政治(Jervis 1998)。此外,大部分的复杂系统研究根本不包括人类。它聚焦于物理、生物和生态系统。因此,人们可以找到磁铁、神经元、蜜蜂、森林火灾和雪崩的复杂系统模型。
在思考社会学和复杂性之间的交集时,我看到了社会学在获取和应用复杂系统模型方面的极大潜力。这样说是因为复杂性科学家的沙盘中包含了大量的模型,其中许多模型可以直接或间接地应用于社会世界。一些模型探讨了一些理论问题,如一个系统是否会产生平衡、复杂性或随机性(Page 2008,Hidalgo et al. 2014,Wolfram 2002),或一个系统如何受到网络结构(Newman 2010,Watts 2004)、相互依赖(Durlauf & Ioannides 2010)、多样性(Page 2007,2010)或学习(Epstein 2014,Vriend 2000)的影响。其中许多模型可以与空间和时间数据相连接,然后应用于从社会组织(Helbing 2010)到文化、思想和疾病的传播(Tassier 2013)等诸多主题。
有些人把复杂系统模型称为跨学科模型,因为它们满足一对多特性。我的意思是,为单一目的开发的模型可以应用于许多其他目的。为探索疾病传播而开发的模型已被应用于犯罪(Akers & Lanier 2009)、肥胖(Akers & Lanier 2009)和歌星贾斯汀·比伯(Tweedle & Smith 2011)的传播。这种应用是通过将一种行为的扩散(例如下载比伯的歌曲)视为一种疾病的传播来完成的。就像一个朋友可能给你带来麻疹,她也可能给你带来比伯热。不同的是,比伯热是在互联网上传播的,而麻疹是在现实世界通过社交网络传播的。但是近似地看,这两种现象都可以被理解为在网络上的传播。
在接下来的章节中,我将描述这些模型所产生的概念、想法和洞见。这些想法被归属于动力学、聚集、分布以及多样性和结构的功能属性等类别。我将依次讨论每一种类别,然后评论社会学内部要吸收复杂性研究的成果需要的改变,以及将新的、大的数据用于这些模型的潜力。为了使文章的其余部分易于理解,我首先简要地描述了复杂性和复杂系统的含义,并介绍必要的术语。
复杂性这一概念可以应用于一系列广泛的系统和现象。大脑、全球金融系统、税收码、国际政治、中学、蛋白质折叠、生态系统和蚂蚁群都可以而且已经被描述为复杂的。鉴于复杂性应用的多样性,人们不能期望用一个单一的测量或统计来捕捉复杂性的本质(Mitchell 2009, Page 2010)。这就产生了一个问题和一个机会。问题在于,要使这个领域从组织理论家 Michael Cohen 曾经说过的“隐喻的节庆”过渡到一门真正的科学,需要有明确的术语和概念,这就意味着需要测量。但是,没有任何一个测量可以捕捉到复杂性概念的无数含义和细微差别。而机会则在于各种测量有可能共同发挥这种作用,因为每一种测量都能捕捉到“复杂性”的部分含义。
现有的一系列测量既可以被看作是一系列五花八门的失败尝试,也可以被看作是各种观点的集合,其中每一种观点都揭示了复杂性的某些方面。我认为后一种描述更为准确。我们可以通过接受多种定义并探索它们的相同点和独特性来获得对复杂性概念的深刻理解。出于这个原因,我将首先对多种不同类型的复杂性的测量进行简要的描述。
有了一组数据就能更好地解释这些测量。考虑一组并发的时间序列数据,也许是标准普尔500指数中股票的每日价格集合,或者是密歇根州安娜堡市塔潘中学学生的智能手机上每天不断变化的播放列表。根据各种测量,每组数据都是复杂的。首先,每一个都很难描述,我的意思是,每一个都需要很多文字来表达。在计算机科学的正式语言中,每个人都有一个相当大的描述长度或科尔莫戈罗夫复杂性。
第二,股票价格和播放列表既不是简单的模式,也不是随机的(Wolfram 2002)。这些数据中既蕴含秩序,又缺乏秩序。第三,如果人们能够识别并去除每组时间序列中的随机性,精妙的结构就会保留下来。物理学家把这些去掉了随机性而得以保留的结构称为预测信息或超额熵(见 Prokopenko et al. 2009)。超额熵(excess entropy)是非随机的不确定性,如果你有足够的时间和正确的模型,你最终可以将这种非随机的不确定性研究明白。而大量的超额熵意味着预测未来值将是一个挑战。
此外,无论是采用自下而上的演化系统还是自上而下的工程方式,每一组序列都很难重现。能够创造出统计上无差别的时间序列集合的最小模型必须包含许多相关的状态[注1]。这个过程被认为具有高度统计复杂性。最后,这些数据也可以被解释为包含大量信息(Adami 2002)。对于播放列表来说尤其如此。它们包含了做出选择时所处的环境信息,这一洞见对社会学家来说应该是熟悉的,但对其他学科来说却比较新颖。
注1:我所说的相关状态是指该过程以非微弱的概率访问的状态。
这些形式上的特征揭示了复杂性的许多方面:具有确定的结构,这一结构可能蕴含着意义,又不容易定义、预测、解释、构建或演化。更简单的说(Page 2010),复杂性可以被认为是 BOAR(介于有序和随机之间,between ordered and random)以及 DEEEP(难以解释、演化、构建或预测,(difficult to explain, evolve, engineer, or predict))。所有这些关于什么是复杂性的想法都被确定为数学测量,并与复杂性的直观概念一致,即复杂的东西并不简单。它很难理解。
正如刚才所定义的那样,复杂性具有现象学的性质。复杂性的存在引出了它如何产生的问题。大多数情况下,它是由复杂系统产生的。这些系统往往有四种属性。首先,复杂系统包含多种不同的实体。这种多样性可能是与生俱来的,就像生态系统中的各种物种一样,也可能是在相互作用的过程中产生的,就像从(几乎)相同的DNA链分化出来的细胞一样。
第二,复杂系统中的不同实体在一个互动结构中相互作用。在某些情况下,这种结构最好被表现为一个固定的网络——一个人在组织层次中的位置可能在短期内是稳定的。在其他情况下,这个网络结构可能更加短暂。我们每天实际接触到的人是一个动态的、永恒的新网络。
第三,个体行为是相互依赖的,即一个人的行动或行为会影响其他人的行为。这种影响可能是巨大的(例如,一个国家对另一个国家的入侵会引起其他人的多种即时反应),也可能是更微妙的(例如,看到一个陌生人的新发型或衣服可能会改变一个人对什么是社会可以接受的这一问题的看法)。
最后,也许也是最重要的,实体能够适应或学习。这些实体不仅改变了他们的行为,而且还改变了他们与他人的联结以及相互依赖关系。适应可以是在实体自身层面,例如社会系统,也可以是在人口层面,例如生态系统。在社会系统中,两种类型的变化都会发生。每个人都在学习或适应。每个组织也都必须学习和适应(否则它们将不能长期生存)。个体和社会如何学习?尝试、模仿和选择都是很重要方式(Vriend 2000)。学习和适应的规则决定了系统的动力学,而系统的动力学反过来又影响了接下来发生的事情(Golman & Page 2009)。
具有这些特性的系统,即所谓的复杂系统,有可能产生复杂性。但它们不需要被称之为复杂系统。一个经济体是一个复杂系统,但经济的许多部分是稳定的和可预测的。因此,使用“能够产生复杂性的系统”而不是“复杂系统”这个术语会更准确(尽管很迂腐)。
上述观点可以更为正式地表达为,无论是由蚂蚁、公司、国家还是跨国公司组成,一个复杂系统都有可能产生多类结果:均衡、多种模式、复杂性和随机性(Wolfram 2002)。这里的模式既包括周期性模式,如商业周期,也包括趋势,如犯罪的减少、对不平等的日益接受,或社会资本的减少(Putnam 2000)。
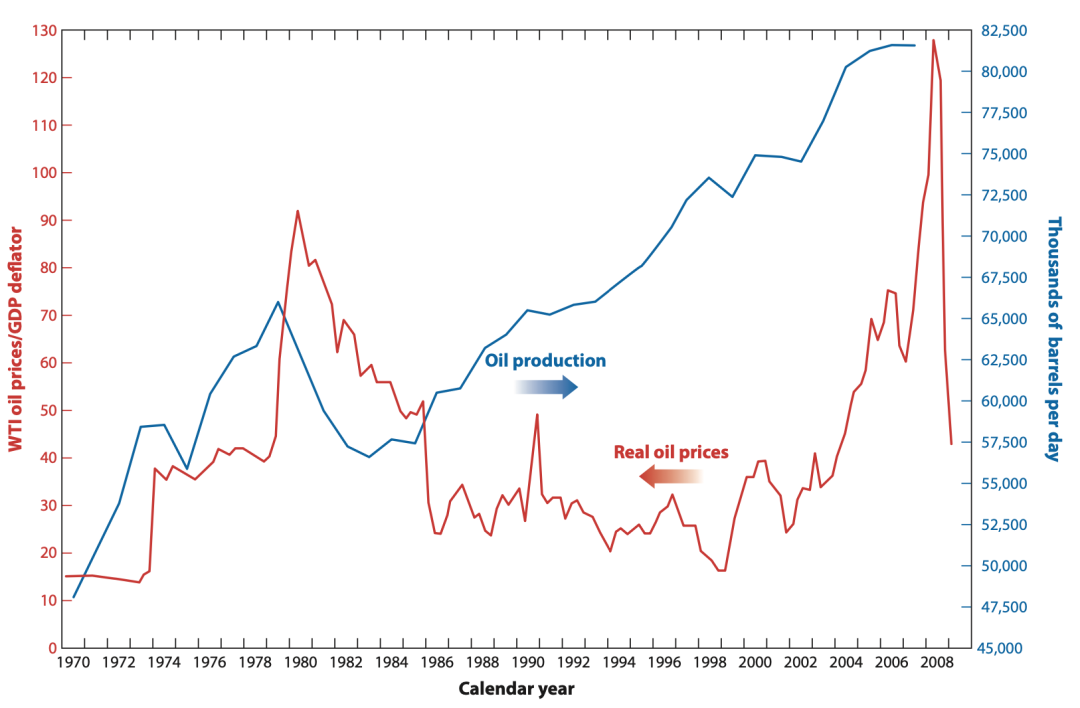
一个特定的复杂系统往往会产生多类结果。考虑一下世界石油市场。过去60年的石油生产图显示了一个近似的线性趋势(海湾战争造成了偏差)。石油生产紧跟全球经济增长,所以它表现出一种简单的模式。而同一时期的石油价格图则显示了复杂性。这个时间序列介于有序和随机之间。它也很难描述、解释或预测(见图1)。一句话,它是复杂的。
在过去的几十年里,复杂系统的一般理论取得了持续但有限的进展(Tao 2012)。我使用复数的一般理论是因为可能不存在单一的一般理论。这一看法建立在一些人所谓的“非大象问题”上,即 John von Neumann 和 Stanislaw Ulam 的一句调侃:非线性函数的集合类似于非大象动物的集合(Fisher 1987)。可能的复杂系统的集合也许太大,以至于能够包含所有这些认识的单一的一般理论不太可能存在。
任何复杂系统的一般理论都有一个问题,那就是它似乎会指出在大脑、经济、城市、天气系统、生态、金融市场、知识界和蚂蚁群中都有相同的现象。真的是这样吗?一方面,显然不是。蚂蚁群不会产生飓风或遭受癫痫发作。另一方面,当然如此。非大象的集合有许多共同的性质。几乎所有复杂系统都表现出聚集的波动性,而且这些复杂系统既表现出稳健性(Jen 2005)又可能产生大事件(Ramo 2009),这很矛盾。许多复杂系统也产生长尾分布,即非正态分布。城市规模、交通堵塞的长度、公司规模、战争死亡人数、物种丰度和引用数量的分布都有长尾。虽然没有一个单一的因果模型可以解释这些类似的分布,但似乎确实有一些基本的原因可以解释大多数情况,例如正反馈、自组织的临界状态,这一点我在下文中会详细地提到。
另一些复杂系统的共同性质包括自组织、涌现、边界和水平(Holland 2014)、路径依赖、阈值现象(又称临界点)、创新的产生(1955年财富500强中几乎没有10%的公司至今仍在该名单上),以及平衡探索与利用之间的张力。这些现象都可以在空间、生物、生态、经济和虚拟世界中找到。如上所述,这就是为什么复杂性科学被认为具有跨学科性质,因为它提供适用于多个领域的概念。因此,即使复杂系统可能缺乏一个统一的理论,该领域仍然包含大量连贯和关联的理解,足以构成一个知识体系。
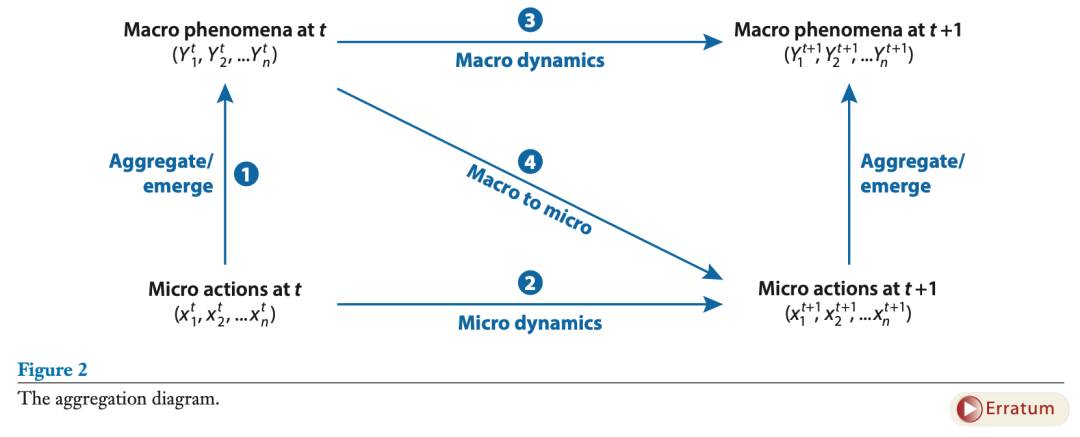
我采用图形表达复杂性理论的研究成果(图2)。该图反映了一个事实,即复杂系统通向科学的途径是自下而上的(Iwasa et al. 1987)。分析的基本单位是主体,而不是一组变量(Macy & Willer 2002)。[注2] 置身于社会空间中的主体被赋予了行动,并不受约束(Epstein 2014, Miller & Page 2007)。系统的聚集行为可能达到一种均衡状态,产生一种模式,或接近于随机性或复杂性。设想把孩子送到营地,把孩子的装备安排在一个小屋里,然后开车离开,让一切发生。
注2:复杂系统模型将主体放在第一位 (Wellman 2014) ,因而将其与依赖总体状态变量之间流量的系统动力学模型区分开来 (Sterman 2000)。
这在图中显示如下。在一个特定的时间点(图中的时间t),一组微观层面的主体(可以是人或组织)采取了行动。这些行动在图中的左下角表示。这些行动聚集在一起,产生更高层次的现象(用Yt表示)。我在图中只画了两个层次;更准确的版本应该包括中间层次(Little 2012)。人聚成群,群体聚集则生成社会。
该图还清楚地表明,宏观层面的变量自身蕴含着动力学。在图的顶部加入因果箭头,使涌现图与科尔曼之舟区别开来(Little 2012)。不同的宏观(中观)层面动力学的可能性部分依赖于自组织和涌现性质的存在:中观和宏观层面的性质不能存在于微观层面(Sawyer 2005)。这些性质可能是系统层面的属性,如稳健性或效率,也可能是更具体的行动,如引导船只到港口(Hutchins 1996)。复杂系统学者不说整体大于部分之和,而是倾向于引用物理学家 Philip Anderson(1972)的话,他写道:“多者异也”(More is Different)。他的这句话抓住了一个事实,即宏观和微观可以在本质上不同。
该图使我们必须尝试用一群主体在微观层面的互动来解释宏观层面的模式、性质和动力学。在物理系统中建立因果联系比较容易,因为分析的基本单位往往是相同的,如碳原子或简单的磁体。社会学的基本单位——人——是独特的,这使得对聚集的理解更加困难。
因此,独特的宏观层面的模式、属性和功能的涌现最好用物理系统来表达。例如,水表现出分子不具备的湿性和粘性等属性。这些宏观层面的属性可以表现出自己的动力学,例如水在岩石上的流动。理想情况下,这些涌现属性及其动力学是可以理解的,比如物理学家理解了波浪的形成,或者社会科学家可以解释人流是如何从微观层面的行为中涌现出来的(Helbing 2010)。但社会科学家并不需要这样物理系统。此外,一些涌现现象仍然保持神秘,比如意识。
从涌现图中可以清晰的看到,复杂系统的视角对可能的微观和宏观现象类型不作任何假设。一个系统可以稳定在一种均衡状态,形成模式,表现出复杂性,或者产生一个又一个完全没有结构的东西。如果我们能写下一个有最大值或最小值的势能函数,使得每当系统不处于均衡状态时,势能至少增加或减少一些固定量,那么我们就知道系统最终会达到均衡。
然而,如果一个系统包括相互依赖关系,例如两方之间进行交易将实质上影响其他人,那么势能函数就不存在。这一点值得解读。在一个集市上(一个纯粹的交换经济体),两个人的交易只有在每个人都受益的情况下才能进行。那些没有参与交易的人是不受影响的。因此,任何贸易都会增加总效用(总福利),所以存在一个势能函数,并且贸易最终必须停止(达到均衡)。同样的逻辑适用于协作博弈(Page 1997)和反协作博弈(Page 2001),例如选择何时去购物,何时去健身房。相反,在国际关系、政治或商业中,一个联盟可能会使组成联盟的双方受益,但可能会损害其他人。总效用可能会减少。因此,我们不能保证这个过程会停止,因为联盟的形成过程并不伴随着普遍的效用增加。系统可能会产生一种模式,或者更有可能产生一种复杂性,而不是一种均衡。
如上所述,在一个复杂系统中,微观和宏观层面都蕴含着动力学。在某些情况下,宏观动力学最好通过微观层面的行为来解释,但在其他情况下则不然(Shalizi et al. 2004)。这些微观层面的行为往往是基于规则和适应性。在约会或配偶选择的复杂系统模型中,主体可能遵循对局部和全局信息做出反应的规则。这些规则将会产生多种模式。随着主体学习这些模式,他们相应地调整他们的行为。其结果可能达到均衡状态,或者更经常的是产生另一种模式。随着时间的推移,该系统很可能产生一连串的非平稳性模式,即复杂性(LeBaron 2001)。
这种在模式上建立模式的想法与宏观经济学中占主导地位的动态、随机、一般、均衡(DSGE)模型形成鲜明对比。在这些 DSGE 模型中,经济被假定为处于一种均衡状态。每个主体都寻求达到均衡状态,并假设其他人也是如此。模型中动力学的出现是由于冲击,以及对于部分寻求实现新的均衡状态的主体的回应。这些模型可以被看作是通往均衡的一系列路径。而在一个复杂系统模型中,主体不具备这样的目的论属性。他们的行动将基于过去的模式。在他们可以预期的未来中,他们不需要做得完美。
如果我们知道主体所遵循的规则,在某些情况下,我们可以通过使用定点定理来证明存在一个均衡状态。然而,均衡的存在并不能保证一群具有学习能力的主体们将会达到这种均衡(Epstein 2007)。复杂系统思想家们的一句口头禅是:“如果你没有演化出来,你就没有证明它。”此外,一个系统可能有多个平衡点;如果有的话,能达到哪个平衡点,可能取决于系统的初始状态、个体如何学习(Golman & Page 2009),或者他们是如何相互连接的(Jackson 2010)。
更准确地说,复杂系统模型表现出对初始条件和路径依赖的敏感性。这一洞察与社会学研究实践有关。例如Salganik等人(2006)的音乐实验室实验。在这些实验中,个人可以选择和下载音乐。在一实验中,受试者不能看到其他人下载了什么音乐。在第二个实验中,他们可以看到其他人下载了什么音乐,结果是人们下载了和别人一样的音乐——这是一种正反馈。而正反馈则产生了一个长尾分布。更重要的是,它们还产生了路径依赖。最终结果取决于过程中发生的结果(Page 2006)。
出于规范性和正面的原因,社会学家对于路径依赖相当感兴趣。在音乐实验室的实验中,下载量最大的歌曲可能得益于运气,也可能得益于技巧。同样地,一篇被引用500次的学术论文的成功也可能归功于正反馈或该论文的学术质量。因此,产品的销售也一样,消费者的选择可能基于别人的选择(Denrell & Liu 2012)。
路径依赖对确定分析同样有影响。结果的偶然性给所谓的对最终结果数据的回归分析带来了问题。忽视动力学因素和只考虑最终的数据可能会导致不正确的推论。这些歌曲和论文的某些特征可能与这些歌曲和论文的下载量有因果关系,但另一些特征可能是特异性的。复杂性的视角迫使人们去探索结果的偶然性,即结果在多大程度上取决于系统中的动态行为。
正反馈只是一个系统许多可能的特征之一,这些特征可以影响系统中的动力学以及结果。非线性动力学的产生有多种原因。它们可能来自人口层面效应。例如,在一个婚姻配对模型中,配对并不发生在总体人口层面。未匹配的人不能代表总体人口,他们改变了剩余个体的配对环境( Xie et al. 2015)。
有趣的动力学也可以通过子空间建设和破坏产生(Holland 2014)。在博弈论中,使用 ABM 方法,重复进行囚徒困境产生了合作的环境,因为主体发展了识别其他合作者的方法。这在行为规则的空间中产生了一个合作子空间(Axelrod 1997)。这样的子空间可能会存在很久,直到一个主体找出如何利用合作者的方法,破坏合作的子空间并产生一个背叛的环境。
聚集是复杂性科学研究成果的第二种类别。复杂系统经常产生反直觉的,甚至是矛盾的聚集结果。学者们已经开发了各种模型,帮助解开聚集的奥秘。这些模型展示了简单的规则如何产生复杂性(Wolfram 2002),以及复杂的微观层面的规则如何在宏观层面产生统计的均衡状态。
微观层面的规则在宏观层面产生统计的均衡状态典型的出现在布莱恩·阿瑟的 El Farol 酒吧问题(Arthur 1994)中。在这个模型中,每个主体必须决定参加每周一次的活动还是呆在家里。每个主体都愿意参加活动,但如果有太多的人参加,他们将不再愿意参加。随着时间的推移,主体将根据过去的一系列的出席人数,决定是不是参加活动。而最理想的参加人数是所有活动出席人数总和的平均数。尽管在微观层面上,该模型是由一个精心设计、不断发展的规则构成的系统,而每周出席人数的时间序列看起来像是围绕着平均值的随机波动。这种微观和宏观之间的脱节也可以在真实的金融市场中看到,在真实的金融市场中,杰出的投资者和团队精心制定策略,但最终的结果是价格的模式几乎是随机的(LeBaron 2001)。
为了描述一些已知的复杂系统中的聚集现象,我首先讨论了复杂系统的属性是如何通过聚集影响复杂性的产生。然后,我将描述多样性、关联性、相互依赖性和学习率的变化是如何导致聚集层面的复杂性增加或减少的。最后,我讨论聚集如何产生自组织和涌现的问题。
在探索聚集的过程中,出现了许多 “假如”问题。假如我们增加这个参数呢?假如我们让主体更有适应性,更多样化,或更少联结呢?为了回答这些问题,必须对传统方法进行扩展。在一个均衡模型中,人们通过改变参数和评估均衡的变化,对模型进行比较静态分析。如果我们降低税收,经济增长会怎样;如果我们加大惩罚力度,犯罪率会怎样;如果候选人消极怠工,选民投票率会怎样,等等。复杂系统模型不一定产生均衡,所以标准的比较静态分析往往是不可能的。因为,如果均衡不存在,我们就不能比较均衡。
同样有问题的是,我们不能只扩大结果的类别,然后对动力学、模式和随机性进行比较,因为改变一个变量可能会改变结果的类别。当一个参数改变时,一个处于平衡状态的系统可能会变得复杂。这样的一类结果变化比人们想象的更常见。从混沌和非线性动力学的研究中,我们知道系统可以从具有单一均衡状态转变为具有两个均衡状态(分叉),或者从均衡状态转变为周期性曲线或转变为随机状态(相变)。
这些结果类别的变化可能在临界值或临界点突然发生。临界点可以是环境性的(即影响系统行为的参数的微小变化),也可以是直接的(即导致系统走向某一特定状态或一类结果的行动)(Lamberson & Page 2012)。当民众变得足够愤怒,有可能发生起义时,就会出现环境性的提示。一个直接的提示是使起义开始的行动。在环境性的提示出现后,变化是不可避免的。而把这种不可避免的变化归结为一个特定的行动可能是不得要领的(Omerod 2012, Watts 2011)。
也就是说,复杂系统的核心属性——多样性、关联性、相互依赖性和适应率——的变化并意味着可以产生任意的结果,也不是说复杂系统是无法理解的。恰恰相反,许多普遍的模式确实存在。最值得注意的是,复杂性不会发生在极端点。复杂性发生在一个介于两者之间的区域(Miller & Page 2007)。
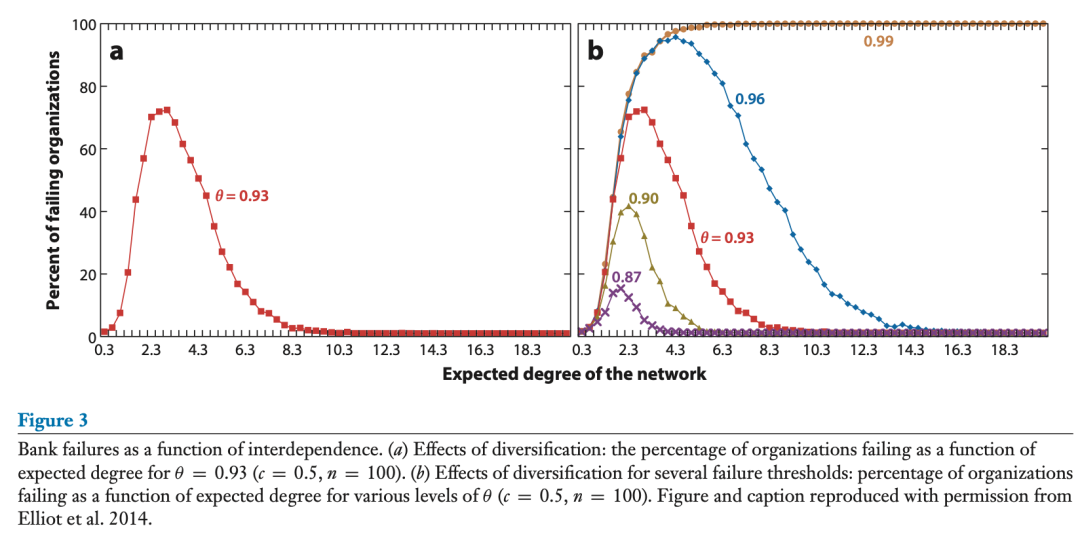
要想知道为什么会这样,可以想象有四个表盘,每个表盘代表一个复杂系统的一个属性,然后想象拨动这些表盘。让我们首先增加连接性,保持其他属性不变。想象一下一些完全没有联系的银行,比如说可能是一百年前的情况。如果一家银行倒闭,不存在任何系统层面的影响。只有这一家银行会倒闭。现在,让我们增加连通性,并假设银行向它们所连接的银行借款和贷款。现在,如果一家银行倒闭,它将不再有能力偿还它从其他银行借来的钱。这可能会导致出借方银行倒闭,并引起传递效应。因此,连接性的增加导致大型事件发生的可能性增加,同时也增加了复杂性——因为每家银行都在其利基市场范围内运作。
现在,让我们进一步增加连接性。如果每家银行都与其他银行相连,那么一家银行的故障就会被系统吸收。此外,每家银行都在一个相同的背景下运作——每家银行都与其他银行相连。这个系统并不复杂。
这些影响在图 3a,b 中很明显。它显示了在Elliot等人(2014)撰写的金融相互依赖模型中,大型银行倒闭的概率作为相互依赖程度的函数。随着互联程度的增加,银行倒闭的可能性也会增加,但随着互联程度继续增加,倒闭的可能性又会下降。
与此相关的是,许多模型考虑了在囚徒困境游戏中玩固定策略的主体,其中更好的策略在人口中增长更快(复制子动力学)。当这些主体被放在一个一维网络中时,没有什么有趣的事情发生。在有三个或更多维度的模型中,一种策略会占主导地位;然而,在两个维度中,所产生的动力学是复杂的。计算机模拟的结果已经在生物学上得到了复现(Kerr et al. 2002)。又一次,复杂性发生在中间地带。
接下来,我们可以调整多样性表盘。如果每个主体都是相同的,那么这个系统就不会复杂。随着我们增加多样性,我指的是行为的多样性,那么系统很可能变得复杂。但是,如果每个主体的行为都是独一无二的,那么微观层面的行为将是随机的,因此在系统层面,大数法则逻辑将适用,结果将是一个统计平衡。在微观层面上,系统可能是复杂的,因为它将很难定义,但它不会产生复杂性。
第三个表盘对应的是相互依赖关系。改变相互依赖关系的效果,也许可以在社会互动模型中得到最好的体现(Durlauf & Ioannides 2010)。考虑一组排列在长方形网格上的主体,他们可以选择两个行动之一,向上(+1)和向下(-1)。在该模型的应用中,这些行动代表选择是否采取一个特定的行为,例如,在学校努力学习,吸毒,或者它们可能代表在两种行为中进行选择。为了启动这个模型,每个主体都从一个初始行动开始——向上或向下。假设这两个行动的可能性相同。
在社会互动模型中,每个主体都有一个具有影响力的邻居。现在,我们可以把这些影响者看作是北、南、东、西四个邻居(伊辛模型)或整个网格(居里-魏斯模型)。这些影响者可以使主体改变其行动。假设有以下行为规则。假设一个主体有(S)概率(面对社会压力)选择与大多数邻居一样的行动。有概率(1-s),主体随机选择。如果 s 很小,那么系统将平均有接近一半的主体选择向上,另一半人选择向下。随着社会压力(s)的增加,系统会出现提示,从而产生有两个均衡,而不是一个:一个是有大量主体选择向上,一个是有大量主体选择向下。在这个临界值,该模型产生了复杂动力和模式。再一次,复杂性发生在中间值的范围内。低社会压力导致没有复杂性(每个行动的数量相等),高社会压力导致同质性。介于两者之间的是复杂性。
很明显,最后考虑改变适应或学习的速度。如果主体遵循固定的规则,那么一些系统可以产生复杂的动力学(Wolfram 2002),但只针对精心选择的规则集。如果适应性转盘被设置得无限高,那么就是假定主体可以理性地预期会发生什么,而且主体将总是采取最佳行动。其结果将类似于假设理性预期的经济模型:均衡。在中间,当主体以更适度的速度适应和学习时,他们会产生总体模式。然后他们学习这些模式并创造新的模式。
复杂系统内的聚集可以产生在微观层面上不存在或不可能存在的模式、功能和特性。这通常被称为涌现。大脑中的意识,社会中的文化,以及(如前所述)水的湿度,都存在于宏观层面,但不能由单一的组成部分来维持。一个水分子不可能是湿的。
涌现可以发生在多个层面。嵌入DNA和环境中的信息结合在一起,产生分化的细胞。反过来,这些细胞的组合形成器官和器官系统。每个层次都有在其下面的层次不存在的功能。类似的特征也适用于人、群体和社会。每种聚聚集产生的实体都有不同的能力,并能表现出不同的属性。
在这里,我讲对涌现和自组织进行了区分。前者是指属性和功能,而后者是指模式或形式。鸟类的成群结队,种族的隔离,以及观众席上个人有节奏的鼓掌都是自组织的模式。意识、文化和集体认知是涌现的例子。在每一种情况下,都有一种功能存在于宏观层面,而在微观层面上并不存在(Hutchins 1996)。
自组织和微观规则。在社会学中,对自组织概念的理解对于解释和评估宏观层面的模式尤为重要。从 Schelling(1971)的隔离模型中可以看出,出现的模式不一定与微观层面的偏好和行为一致。在他的模型中,Schelling(1971)假设了一个同质的、基于阈值的搬家行为规则——如果邻居中属于同一种族群体或收入阶层的人少于一个固定的部分,人们就会搬迁。他发现,即使有一个(相对)宽容的阈值,系统也会自我组织成隔离的社区。
这里我们发现了一个微观和宏观之间的脱节。但是,这发生在一个极度非写实的模型中,这并不是现实主义的。谢林的模型假设了一个同质的阈值规则和两种类型的主体以同等比例存在。他没有努力对他的模型进行校准。
Bruch & Mare(2006)考虑了一个更合理的带有概率成分的线性行为规则(实际上是一个随机效用模型)。他们还将自己的模型与底特律地区研究中得出的偏好进行了校准。Bruch & Mare 的原始分析显示,隔离现象远比 Schelling 的模型要少。Bruch & Mare 的结果受到了 van de Rijt 等人(2009)的质疑,他们发现了一个编码错误,确定了在有误差的线性规则下隔离更加极端的参数,并表明如果随机成分足够大,隔离会减少。
Bruch & Mare(2012)随后的分析表明,隔离的程度如何取决于线性规则的斜率和误差项的大小。与此相关,Xie & Zhou(2012)展示了隔离是如何被个人层面的异质性削弱的,因为更宽容的个人将种族混杂的社区联系在一起。
我做这个简短而不完整的回顾的原因有两个:把谢林模型及其前身作为自组织的例子,并强调主要结果的稳健性。人们可以将阈值规则改为线性规则,可以提高或降低随机的程度,可以使主体异质化,对于相当大的参数范围,系统将产生某种程度的隔离(Bruch 2014)。这是因为搬迁会产生两种类型的正反馈。首先,它增加了旧社区中与搬迁者相同类型的个人想要搬迁的概率。第二,它增加了新社区中与搬迁者相反类型的个人想要搬迁的概率。这些正反馈产生了一种放大作用,这种放大作用表现在隔离上,超出了偏好的线性评估所能表明的范围。
种族隔离是自组织,因为它是一种模式,而不是一种新的功能,如意识,这些功能是涌现的。而自组织和涌现之间的区别比人们想象的要模糊,因为模式也可以有功能。社会网络的小世界属性(Watts 2004)可以被认为是涌现的。小世界网络的平均路径长度很低,俗称六度分隔现象。人们建立网络的目的并不是为了在五个步骤内连接到音乐家温顿-马萨利斯(Wynton Marsalis),但他们的网络允许他们这样做,而且这一特征的出现并不是有任何人有意为之的。
社会系统中的涌现有多种形式。在此,我重点讨论两种形式:系统的稳健性和群体层面的现象。许多复杂系统,例如,我们的大脑、我们的身体、生态系统、经济、政治系统(Bednar 2008)和互联网等等,都表现出显著的稳健性。即使这些系统中的主体的主要动机不是系统的稳健性,而是个人的成功,也会出现这种情况。这可以归结为智能系统的设计。但是除了政治系统之外,很少有社会系统有设计者,甚至那些设计者的控制能力也很有限。[注3]生态系统没有建造蓝图,大脑同样没有。
注3:关于设计的文献着重于创建具有有效且均衡的系统,而不是稳健的结果。(Page 2012, Reiter 1977).
在一些系统中,稳健性的出现是因为各部分的适应性。主体拥有或演化出使他们能够对内部动力学和外部刺激做出反应的能力(Jen 2005)。如果每个类型的主体保持活力,那么系统也会保持活力。系统中许多部分都具备适应能力意味着该系统具备稳健性。行为可塑性在集合体理论中找到了呼应,其中的集合体的组成部分可以在系统之间移动(DeLanda 2006)。因此,集合体可以执行各种功能,而不是一个特定的功能。请注意,集合体系统会因适应而发生变化,所以它不应被看作是一个固定的实体。这就是为什么复杂性科学家将稳健性与稳定性区分开来。稳定的系统会返回到以前的平衡点。稳健的系统不断地适应,但也许是以不同的方式。
当然,稳健性的反面是系统性风险(见Centeno et al. 2015)。正如稳健性可以是一个涌现的属性一样,大型事件的可能性也可以是一个涌现的属性。如上所述,复杂系统经常产生大量小规模事件,偶尔也有大规模事件发生。缺乏一个中央计划者应该是一个值得关注的原因。一个复杂系统并不保证是稳健的。
接下来,考虑群体层面的功能的涌现。在社会系统中,群体可以被认为是一个集合体,而群体的属性可以区别于并超过个人的属性(Sawyer 2005)。就像大脑可以完成远超过任何一个神经元的能力一样,群体也可以完成任何一个人都无法完成的任务。Hutchins(1996)提供了一个关于没有一个人如何引导一艘船入港的说明。这种能力是一种由个人组成的交流网络的属性。管理任何组织或整个社会运作的能力同样如此。没有人管理经济。它的运作或失败是个人行动聚集的一个涌现属性。
涌现发生在各种各样的环境中的多层次的聚集中。爵士乐三重奏的卓越表演、运动队的精彩演出以及令人屏息的莎士比亚戏剧都是涌现的。它们不是各个部分的属性。它们的存在取决于个人之间的联系和沿着这些联系发生的交流(Sawyer 2005)。
在一个复杂系统内,关键实体往往是多样化的。因此,对一个复杂系统的分析既要注重描述这种多样性,又要考虑其影响。我首先讨论分布情况,然后讨论多样性水平的影响。
即使所有的主体一开始都是相同的,他们往往可以学会采取不同的行动,所以多样性水平将是内生的。此外,由于复杂系统经常产生的是到达结果的路径,而不是均衡,所以在对因果效应进行规范的和有效的评估时,人们必须经常比较结果的分布,而不是均衡。最重要的是,复杂系统中的相互作用意味着分布往往是非正态的(Weaver 1948)。因此,为了理解一个复杂系统,人们需要知道的不仅仅是平均值和变异值。人们还需要分析完整的分布,无论是行为、结果还是持续时间。
在许多情况下,这些分布是长尾的。与正态分布的变量相比,它们有更多的小事件和更多的大事件。对长尾现象的一种解释是,复杂系统包括正反馈和负反馈。正反馈产生长尾的原因很明显。更多的东西会产生更多的东西。负反馈产生长尾的原因则不同。请记住,长尾是相对于整体变化而言的。通过减少波动,负反馈降低了变异,增加了尾巴的相对长度。想象一下,在一个系统中,负反馈或正反馈都占主导地位。当前者占主导地位时,系统会产生大型事件。当后者占主导地位时,系统产生更多的小事件。在每种情况下,结果的分布都是(相对)长尾的。
正态分布的产生于中心极限定理,而长尾分布的产生则有多种原因。在这里,我描述了四个可以产生长尾的过程。第一个过程是乘法效应。如果随机冲击被相乘而不是相加,那么产生的分布将是对数正态。许多复杂系统模型包含了复制者动力学,其中种群中的类型数量与该类型的相对健康度成比例增长。这是一个乘法效应的例子,因此也会产生一个长尾。[注4]
注4:几乎在所有的生态系统中,物种的丰度都呈现出长尾分布。(Hubbell 2001).
尽管对数正态分布的尾部比正态分布长,但许多复杂系统会产生一个甚至更长的尾部分布,即幂律。[注5]幂律可以由几个模型产生,其中与社会学最相关的有三个(Newman 2005)。
注5:在幂律分布中,一个大小为x的事件的频率可以写成x的负幂。
第一个模型是优先连接,它捕捉到了马太效应(Merton 1968),即富人变得更富,使穷人变得相对更穷。在优先连接模型中,新的实体依次到达。想象一下,第一个人创造了一个类型。对于后来者,假设以接近1的概率,选择一个现有的类型;以剩余的小概率,创造一个新的类型。如果一个人选择特定类型的概率与该类型的相对人口成正比(越多越好),那么产生的分布将是一个幂律。[注6]
注6:回想一下关于音乐实验室实验的讨论,即使我们可以预测结果的分布,路径依赖也意味着我们将无法非常准确地预测给定类型在该分布中的位置。
例如,如果一个人搬到一个城市或在一个公司工作的概率与城市的人口或公司的规模成正比,那么城市规模和公司规模将服从幂律分布。乍一看,两者都是幂律分布,学术论文的引用次数、网站链接、城市中的产业和图书销售都是是如此(Bettencourt & West 2010, Newman 2003)[注7]。城市、互联网和引文都被同一个模型所涵盖。这些非大象有一个共同的特点。
注7:参见Shalizi(2013)对这些分布的拟合的批评。
第二个产生幂律的模型依赖于一种叫做自组织临界的现象(Bak 1996,Hidalgo et al. 2014)。想象一下,把沙粒丢在桌子上直到形成一堆。这堆沙子是一个临界状态:即当你加入一粒沙子时,存在着发生雪崩的可能性,这是一个大事件。一些模型表明,交通也可能演变成一种临界状态(Nagel & Paczuski 1995)。司机可能会选择进入高速公路,一旦上了高速公路,就会在相邻的车辆之间留下空隙,这样整个系统就会准备好产生大型事件。一些学者认为,同样的逻辑可能适用于金融网络、国际政治协议、电网,甚至是不同社会的社会结构(Centeno et al. 2015,Goldin & Mariathasan,2014)。这些都是值得探索的直觉。而复杂系统模型提供了这样做的工具。
请注意,优先连接模式在人群中产生幂律,例如城市、公司、引文数量;而自组织临界性在事件的规模中产生幂律分布,例如雪崩、市场崩溃、交通拥堵和战争死亡。第三个模型,随机游走返回时间,解释了持续时间的幂律分布。回顾一下,在一个复杂系统模型中,我们经常从为主体分配类型开始。想象一下,每种类型的主体的数量遵循随机游走;也就是说,在每个时期,它增加1的可能性和减少1的可能性一样。然后可以证明,持续时间在类型上的分布将是幂律(Newman 2005)。
复杂系统中长尾分布的占优是令人惊讶的。大多数情况下的标准假设是正态分布。任何偏离正态的情况都需要解释。而在复杂系统模型中,在许多情况下,长尾分布应该是结果;因此,任何非长尾分布的大小都必须得到解释。在社会学背景下,人们可能会被迫证明近似正态分布是否应该出现(通过中心极限定理的思维),或者是否是社会强加的结构性约束导致了长尾的出现。
复杂性科学中最后一组与社会学有关的发现,涉及多样性和结构的功能属性。多样性(不同的类型)和变异(在一个类型中的区别)在社会学中的作用比在经济学和政治学中的作用要大,尽管它们在生态学和人类学中的作用还没有那么大——在生态学和人类学中它们是基本概念。借用不太恰当的说法,生态学的基本问题可以表述为“为什么我们能看到多样性(人类同样也是多样性的例证)”。
社会学家们从分类和连续两方面来捕捉多样性。前者的例子包括社会经济阶层、种族、民族或性别的区别,后者的例子包括容忍度(Xie & Zhou 2012)、年龄或抵御风险的能力。尤其是社会学和人口学,比经济学和政治学更强调多样性。复杂系统能够为多样性的解释和欣赏提供的是一些洞见,即多样性的多种功能作用。
复杂系统研究发现了多种不同行为的贡献。它们可以促进系统的稳健性或不稳定性,发出相位转换的信号,通过更快的系统级学习来推动创新,并支持集体智慧的现象(Page 2010)。多样性的第一个最容易理解的功能作用是对稳健性和不稳定性的贡献。阿什比的多样性法则解释了多样性是如何增强稳健性的。一个有更多类型的系统可以对更多类型的扰动做出反应。你不能用螺丝刀砍倒一棵树,也不能让一个乞丐来医治伤口。
一个系统中的反馈决定了多样性是否能增加稳健性。如果反馈是负的或者只是弱的正的,那么多样性就会增加稳健行,因为最极端的人首先行动,分散了动力学。如果反馈是强正的,那么异质性就会产生不稳定性,因为一个人采取了行动,导致另一个人也这样做,这反过来又导致更多的人采取行动(如发生在暴乱的模型中,Granovetter 1978)。请注意,在上述的种族隔离模型中,即使存在正反馈,它们也足够弱,以至于增加多样性会减少隔离(Xie & Zhou 2012)。
多样性的第二个作用,即变异的增加如何能发出提示或相变的信号(Scheffer et al. 2009),依赖于以下逻辑。当一个系统即将发生变化时,例如从一个平衡点到另一个平衡点,以前的平衡点会变得不那么强大。这在景观上被模拟成一个不太陡峭的适应性高峰。选择的力量就会减少,使峰值变平。这种扁平化使更多的变异成为可能。变异预示着寻求新的峰值,即对系统的改变。
多样性也可以与创新联系起来。对于生物系统来说,费雪的基本理论指出,进化系统中的适应率与变异的数量成正比。这里的逻辑也是很直观的。更多的变异意味着更多的高适性和更多的低适性个体。前者会提高适应率。在社会背景下,多样性,以独特的表征和解决问题的工具的形式,可以通过减少共同的局部优化的数量来加速学习(Page 2007)。当一个人卡在一个问题上时,另一个人很可能会找到出路。
最后,感官器官和模型的多样性有助于集体智慧的形成。回顾一下,在一个复杂系统中,每个人都置身局部;他们可能有不同的信息和经验。这种情况下多样性产生了主体如何解释他们的世界的多样性。因此,多样性产生了多样性。这种多样性的结果是,集体可以比其中的任何成员更准确。可以证明,一个多样化的人群必然比其成员的平均水平更准确(Page 2007)。
稳健性、创新性和集体智慧这些属性中的每一个都是涌现出来的;因此,它们可以被包括在上一节中。然而,它们出现的程度取决于系统所保持的多样性。而且,正如已经提到的,过多的多样性会阻止结构的出现。转盘拨动的太远。因此,复杂系统经常在探索新事物和利用成功事物之间取得平衡,以便它们既不至太少也不至太多多样性。
多样性也有助于动力学的产生。作为一个思想实验,想象一个由大小相同的实体集合组成的系统。假设每个实体都有价值或重量,在其当前价值的某个固定百分比范围内波动。该值的时间序列将呈正态分布,波动幅度相对较小。现在假设实体的价值是按照幂律分布的,同时假设价值波动也服从幂律分布。总数表现出更大的波动性,因为平均数将是不均匀的。大型实体的波动将产生重大影响影响。这个思想实验可以很好地解释大缓和,即美国经济从 20 世纪 80 年代中期开始并持续了近 20 年的稳定。在此期间,由于从通用汽车等大型制造商向沃尔玛等大型零售商的过渡,公司规模的分布不那么长尾了(Carvalho & Gabaix 2013)。
正如多样性在复杂系统中发挥着功能作用一样,结构也是如此。社会学的大量文献表明,个人在社会中的地位如何有助于获得权力、影响力和社会资本(Burt 1992, 2005)。复杂系统模型经常分析整个结构的影响(Omerod 2012)。例如,Golub & Jackson(2012)发现,学习的速度取决于同质性的程度。在他们一篇很有影响力的论文中,Centola & Macy(2007)发现,长纽带在直觉上被认为会加速创新扩散,当创新需要强化时,会产生相反的效果。与此类似,Lloyd-Smith等人(2005)表明,超级传播者或高度联系的人可以使一种疾病的传播比假设随机混合的模型所预测的要快得多。
多样性和结构也是相互影响的。Padgett & Powell(2012)最近的工作详细描述了网络结构和多样性的相互依赖的功能方面。作者解释了不同主体如何构建关系网络,以及这些关系如何创造利基。这些利基反过来又为新类型的主体创造了机会。为了简化丰富的、基于经验的一系列模型和案例,Padgett和Powell展示了人如何创造网络,网络如何创造人。因此,多样性可以在结构的背景下被理解,而结构可以部分地被理解为多样性的结果。
Padgett和Powell的逻辑的核心是,嵌入结构中的不同主体可以产生功能子结构,即自动催化的一系列行为。这些集合可以被宽泛地认为是各种活动的良性循环,可以被看作是涌现的功能。自动催化的互动存在于多个网络中——社会、政治和经济。这些连通的网络使得有益的连接成为可能进而导致创新,因为主体与一个领域有关联往往意味着在该领域有共同的利益。
在这篇文章中,我描述了复杂系统研究如何提供对主流社会学家感兴趣的话题有直接影响的模型、想法和见解,以及社会学如何可能从对复杂性研究的更深入参与中受益。我没有重申文章正文中的观点,而是以三点意见作为结束。
首先,社会学和复杂性之间的关系是路径依赖。社会学形成时,复杂性科学还不存在。这意味着,只有当社会学家首先发现了的复杂性科学的核心思想,才能在社会学中占据核心地位。在很多情况下,比如在聚集的悖论和网络结构的重要性等方面,这是真的。不过,想象一下,如果时机不同,复杂性科学在社会学创立之前就已经被全面阐释了(顺便说一下,这并没有发生)。鉴于这两门学科之间的共鸣,复杂系统可能被认为是社会学研究的基础。
其次,大数据的可用性意味着社会学家有时可以将复杂系统模型与数据结合起来。现有的网络层面的数据和分布数据,即使在十年前,要收集这些数据也是不切实际的。第三,可以通过互联网观察社会互动。人们还可以通过互联网进行类似甚至模仿现实世界互动的实验(见Watts 2011的深入评论)。这一观察与前一个观察相联系。大数据正日益成为现实世界的一部分。诸如购物、约会、发表意见、探索想法和享受乐趣等活动过去主要发生在现实世界里。大数据是无法收集的。因为现在许多这些活动都是在互联网中进行的,它们可以被捕捉到以创造大数据。
所描述的一切并不意味着对复杂性模型和思想的吸收将是容易的。基于经验的复杂系统模型需要新的方法论的路径。首先,他们对行为的微观层面的假设必须符合个人的行为。这看起来像是拟合假设,在某种程度上也是如此,但把这看成是对聚集图微观层面的估计更为恰当。其次,模型的宏观预测也必须与经验估计的微观层面的行为一致。最后,宏观层面的预测必须得到支持,也就是说,不能被数据拒绝。
换句话说,(a)模型中的微观假设必须符合微观数据,(b)微观行为必须产生宏观属性(这里人们经常使用基于主体的模型),以及(c)模型中出现的宏观属性必须符合宏观的数据。这些都是高难度的障碍。那些成功完成这三项任务的社会学家(见Bruch & Mare 2006, 2012; Centola & Macy 2007),不出所料地得到了该学科的认可。
最后,尽管复杂性科学还远远称不上完整,但它提供了大量且不断增长的有用模型和见解。它们来自不同的学科,涵盖了一切。从网络结构的作用到多样性的功能价值。来自物理学、生理学和生态学的模型可以为社会学提供有价值的想法(May等人,2008)。尽管这没什么争议,但却指出了一条不常走的路。但应该有人来走这条路。通过参与和应用更丰富的模型,社会学家扩大了他们看待社会世界的镜头,并改善学科。总而言之,社会学家应该倾听,“房间里的大象”(沉默的学科)有话要说。
计算社会科学作为一个新兴交叉领域,越来越多地在应对新冠疫情、舆论传播、社会治理、城市发展、组织管理等社会问题和社科议题中发挥作用,大大丰富了我们对社会经济复杂系统的理解。相比于传统社会科学研究,计算社会科学广泛采用了计算范式和复杂系统视角,因而与计算机仿真、大数据、人工智能、统计物理等领域的前沿方法密切结合。为了进一步梳理计算社会科学中的各类模型方法,推动研究创新,集智俱乐部发起了计算社会科学系列读书会。
【计算社会科学读书会】第二季由清华大学罗家德教授领衔,卡内基梅隆大学、密歇根大学、清华大学、匹兹堡大学的多位博士生联合发起,进行了12周的分享和讨论,一次闭门茶话会,两次圆桌讨论。本季读书聚焦讨论Graph、Embedding、NLP、Modeling、Data collection等方法及其与社会科学问题的结合,并针对性讨论预测性与解释性、人类移动、新冠疫情、科学学研究等课题。读书会详情见文末,欢迎从事相关研究或对计算社会科学感兴趣的朋友参与学习。
详情请见:
数据与计算前沿方法整合:计算社会科学读书会第二季启动