Nat.Commun.速递：超图中超边和重叠社团的推断

导语

超图（Hypergraph）是对任何数量的系统单元之间的结构化相互作用的编码，最近被证明是描述许多现实世界生物和社会网络的成功工具。近日发表于 Nature Communications 的一项研究提出了一个基于统计推理的框架来描述超图的结构。该方法允许以一种高效的方式推断任何大小的缺失超图，并联合检测存在高阶互动的重叠社团。将该方法应用于各种现实世界的系统，显示出在超边预测任务中的强大性能，检测出与互动所携带的信息完全一致的社团，以及对增加的噪声超边的稳健性。这项研究的方法说明了超图概率模型在为具有高阶互动的复杂系统建模时的基本优势。

关键词：复杂网络，超图，社团检测，超边预测

刘志航 | 作者

梁金 | 审校

邓一雪 | 编辑

论文题目：

Inference of hyperedges and overlapping communities in hypergraphs

论文链接：

https://www.nature.com/articles/s41467-022-34714-7

1. 用于表示高阶交互系统的超图

在过去的二十年里，从社会和技术系统到人脑，网络已经被应用于绘制和描述各种具有互动关系的复杂系统。然而，在过去几年里，诸如细胞网络、大脑结构和功能网络、社会系统、生态系统、社会图像搜索引擎、人类面对面的互动和协作网络等各种复杂系统都表明，很大一部分的互动是在三个或更多的节点之间同时发生。因此，这些高阶系统很难使用传统的图表示方法进行描述。

于是超图（hypergraph）的分析框架被提出，其中任意维度的超边（hyperedge）可以编码任何数量的系统单元之间的结构关系。有趣的是，这一复杂系统高阶交互的分析方法，已经被证明可以描述系统扩散、同步、传播和进化等集体现象的涌现。

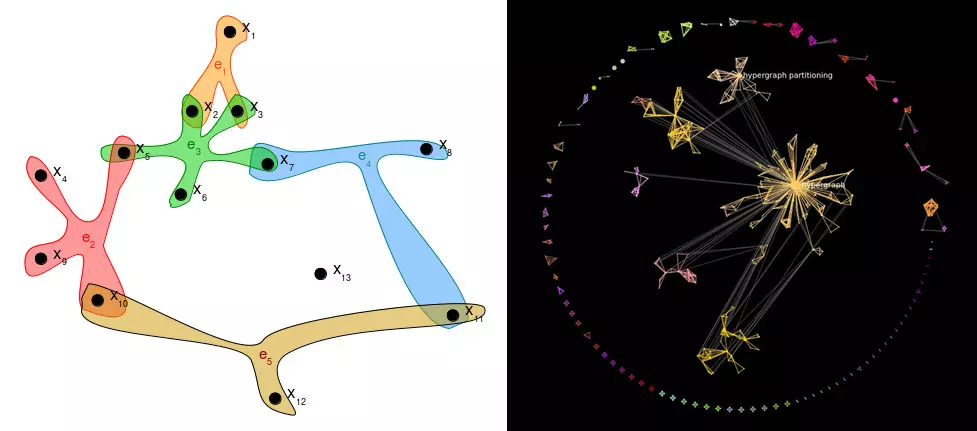
图1. 超图表示及可视化。| 来源：Ouvrard Brunet, Xavier. (2020). Hypergraphs: an introduction and review.

为了正确描述现实世界网络的高阶组织，人们提出了各种增长和平衡模型，如广义配置模型。来自拓扑学数据分析的工具使得人们可以深入了解现实世界网络的高阶组织，并提出了从成对记录（pairwise records）中推断高阶互动的方法。最后，一些强大的网络指标和想法已经被扩展到了配成对的网络之外，从高阶聚类、谱分析方法和中心度到模体和网络骨架。

但如何定义和识别现实世界超图的中尺度组织，仍然是一个很大程度上没有探索过的话题。这项研究基于概率生成模型，提出了一种新的原则性方法来提取基于统计推理的高阶社团，它通过直接从观察到的相互作用中推断出的潜变量，纳入先验的社团结构。它不仅可以检测到重叠的社团，能更好地代表节点预计属于多个社团的情况；它还为执行链接预测任务提供了一个自然的衡量标准，因为它可以输出任何节点子集之间存在一个给定超网格的概率。同样，它允许生成具有给定社团结构的合成超图，这种成分可以在输入中给出或从数据中学习。

2. Hypergraph-MT 模型及其优势

这篇文章介绍了 Hypergraph-MT，一个具有混合成员社团结构的超图的概率生成模型。基于统计推理框架，以提取网络系统中的重叠社团。其核心部分是假定节点属于不同数量的组，由一组成员向量指定。然后，这些成员资格决定了任何节点子集与一个超网格相连的概率。其中潜变量集由 θ = ( u , w ) 定义，其中 u 是 N × K 维的社团成员矩阵， w 是亲和力张量，它捕捉了兼容社团的节点之间更有可能存在的互动。因此，该模型的核心目标就是是在观察到的超图 A 下推断出潜变量u 和 w ，即 P = (A|θ)。

该方法首次提出了在具有高阶互动的网络系统中提取节点的重叠社团组织的方法。除了检测社团，这项研究的模型还提供了一个原则性的工具来预测缺失的超图，从而作为一个定量的评价框架来评估拟合的好坏。在缺乏元数据的情况下，这一功能在评估社团检测方案时特别有用。在实践中，这项研究的模型考虑了一个同种亲和矩阵，这使得它的算法实现具有高度可扩展性。计算复杂度也因在每次更新中以低成本计算昂贵数量的有效程序而大大降低。

论文作者将该模型应用于各种社会和生物超图，讨论了超图和社团结构推断任务的准确性。在一个高中数据集构建的示例中，模拟了一个事件，其中有 10 个外部人员（来宾）和 10 个现有节点的随机子集参与，图 2 中绿色节点是外部客人，而蓝色和橙色节点分别是从两个班级随机选择的学生。Hypergraph-MT 模型不会因这个单独的大超边（灰色）的存在而产生偏差，并且并且它通过为两个类分配零成员资格来很好地恢复外部客人。相反，以往的超图社团检测算法（Graph-MT）会将客人分配到蓝色班级。通过这个示例，作者展示了该方法在发现复杂系统中尺度结构方面具有优势的可能场景，因为这种表示对添加嘈杂的超边更具韧性性，并且在检测社团方面更加稳健。

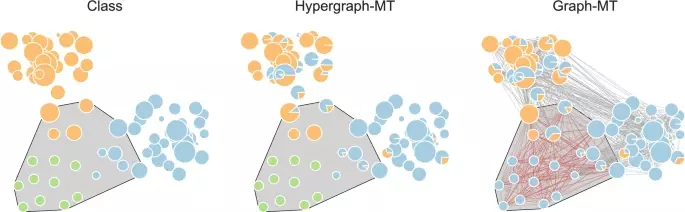
图2. （左）显示了一个高中数据集的一个子集，节点属于 2BIO1（浅蓝色）和 MP*2（橙色）类，以及十个外部客人（绿色）。节点大小与度成正比。灰色的超网模拟了一个事件，为了视觉上的清晰，这项研究省略了其他的超网格。（中）显示了由 Hypergraph-MT 提取的分区，（右）这项研究发现了由 Graph-MT 提取的分区。在后者中，灰色的边表示事件发生前图中的相互作用（通过 clique expansions 获得），红色的边是由于模拟事件而增加的相互作用。这个例子显示了使用与传统的网络分析方法相比超图的优势，因为这种表示方法对增加一个嘈杂的超图更有韧性，在检测社团方面也更稳健。

3. 超边预测和重叠社团的可解释性

该方法在超边预测上也具有很大的优势，作者将其应用于高阶基因疾病数据集的分析，其中节点是基因，超边连接与疾病相关的基因。如图3所示，与以往提出的超边预测算法（Graph-MT和Pairs-MT）相比，在改变最大的超边尺寸D，可以观察到在D=15、16附近的性能有一个强烈的转变，其中Hypergraph-MT明显优于Graph-MT和Pairs-MT。这表明，该模型对大的噪声超边缘的增加更有弹性，可以量化最大超边尺寸对性能的影响，并揭示出临界尺寸的存在，超过这个临界尺寸，Hypergraph-MT算法可能会明显优于动态图（Graph-MT）方法。

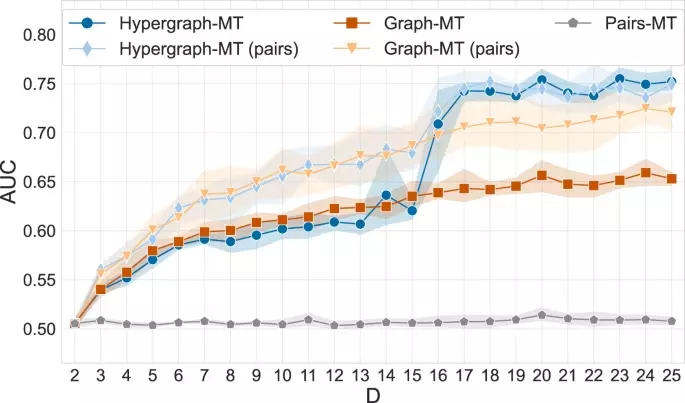
图3. 基因疾病数据集中超边缘预测的临界大小，通过改变最大超边大小 D 来测量 AUC。结果是 5 倍交叉验证测试集的平均值和标准差，AUC 的基线是随机值 0.5。在超图 (Hypergraph-MT)、通过 clique 扩展获得的图 (Graph-MT) 以及仅由已注册的成对交互 (Pairs-MT) 给出的图上运行模型。为了与 Pairs-MT 进行平衡比较，对于 Hypergraph-MT 和 Graph-MT，还测量了大小为 2（对）的测试超边子集的 AUC，同时仍在整个训练集上进行训练。该图显示存在临界超边尺寸，超过该尺寸，高阶算法明显优于替代方法。

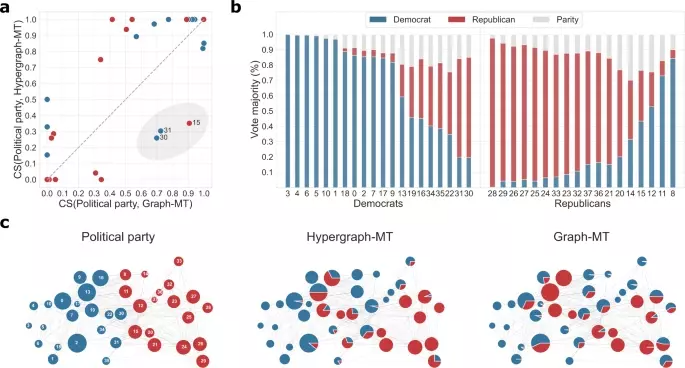
与超边预测一样，Hypergraph-MT 还允许提取有关真实世界超图的中尺度组织的相关信息。作者分析了美国最高法院大法官从 1946 年到 2019 年的所有投票。法官是节点，超边连接在给定案件中表达相同投票的法官。将推断的社团与大法官的政党（即民主党或共和党）作为节点元数据提供的信息进行比较，使用余弦相似度 (CS)，这是一种衡量向量之间距离的指标，因此它更适合捕获混合成员社团。 CS 在 0 和 1 之间变化，其中 1 表示推断的分区与政治派别显示的分区完全匹配。

图4. 美国大法官共同投票的高阶数据集中重叠社团的推断。（a）逐点比较Hypergraph-MT和Graph-MT得到的余弦相似度（CS）。对于每个大法官（图中的标记），由这些方法推断出的社团和大法官的政党之间的CS，即民主党（蓝色）和共和党（红色）。（b）每个大法官的超边缘的投票多数比例。每一个hyperedge都根据参与其中的大法官的多数政治党派进行着色，即民主党、共和党或平均分配（灰色）。然后，对于每个大法官，我们提取他们参与给定多数派的超边缘的次数百分比。（c）根据政党（左）的数据分区，以及由Hypergraph-MT（中间）和Graph-MT（右）推断出的混合成员社团。节点大小与程度成正比，节点标签是Justice ID，交互作用是投影图的边。

通过图 4b 可以发现，大法官始终与自己的政党多数人投票（例如，3号大法官主要与其他民主党人投票，28号大法官主要与其他共和党人投票），但也有大法官的政党与他们的超边所表达的投票行为不一致的情况。例如，节点30（Ruth Bader Ginsburg 大法官）与民主党有关，但她的大部分投票与共和党大法官的投票一致。这种行为被Hypergraph-MT捕捉到了，它给她的成员资格在由共和党人组成的社团中更加突出，而在民主党人的社团中只有一部分，如图3c所示。相反，Graph-MT 将她主要分配到民主党人的社团。这种超图信息和政治归属之间的不匹配解释了图3a中 Graph-MT 较低的余弦相似度值。对于节点31和15也可以得出类似的结论。更为普遍的是，由Hypergraph-MT 推断的重叠成员关系比由 Graph-MT 推断的成员关系更符合大法官的投票行为。

总之，Hypergraph-MT为推断大规模超图的结构提供了一个快速和可扩展的工具，有助于更好地理解现实世界高阶系统的网络化组织。

高阶网络社区

随着对现实世界探索的不断深入，人们发现在许多真实的复杂系统中，组成系统的个体之间不仅存在二元交互关系，也广泛存在多个体同时（或以特定顺序）进行交互，即高阶交互现象。为此，研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型，为复杂网络分析和研究提供了新的思路。

由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学（北京）管青老师在集智俱乐部联合发起了【高阶网络读书会】。读书会围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨，按照「基础理论」+「深入理论」+「案例研讨」的模式展开。读书会第一季已经圆满结束，第二季正在筹备中。现在报名加入可以解锁第一季全部录播视频并加入社群交流。