粒子运动、信息传播、交通人流等等一系列复杂系统中输运问题都可以用图和复杂网络来描述。尤其是利用图论中的“圈”(闭合路径),可以良好地刻画非平衡系统中的输运。同济大学声子中心任捷教授团队近期在Physical Review Letters发表论文,从状态空间中圈的角度,利用“圈流排序”新方法来分析主导圈的行为特征,进而理解物理系统的本质。该工作利用圈流排序方法,在量子热输运问题中有了新发现。
关键词:量子热输运,非平衡系统,圈,圈流,圈流排序,图论,复杂网络
论文标题:
Cycle Flux Ranking of Network Analysis in Quantum Thermal Devices
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.067701
输运是一个在科学研究或者日常生活都很重要的概念,通常描述了在某一空间中,粒子(或者其它研究对象)在非平衡条件的驱动下具有方向性的从一点到达另一点的过程。例如,双十一网购节后大量的快递通过高速公路、航空等方式从商家发往购物者;或者大都市里的地铁线路,定时定点定向的保证大家每天的通勤与出行需求。往往这些具有强大功能的输运体系,在空间中(实空间、状态空间、相空间等)都会形成形成一个错综复杂的网络结构,而非仅仅单一路径。例如我们所熟知的Internet网络,其拓扑结构有多种多样,总线拓扑结构、星型拓扑结构、网状拓扑结构、树形拓扑结构等都对应着复杂网络结构,承载着信息的上传与下载功能;除此以外河流作为人类文明形成的重要元素和重要的运输路径,也具有着网络的特点,小溪汇入小河,支流汇入主干河流,最终流入大海,形成了错综复杂的水系网;甚至更相关到人类身体构成,血管也是具有十分复杂的网络结构。
上图中血管结构构成一个网络,人体血液从左心室泵出,经大动脉—中动脉—小动脉—微动脉,进入微血管网,然后经过微静脉—小静脉—中静脉—大静脉,最终经上腔静脉汇入右心房,经肺循环回到左心室,血液再次从左心室泵出,如此循环不止,生命不息。以上例子都表明了输运往往具有一定的网络结构。如何量化复杂网络与输运之间的联系呢,带着这个疑问我们继续向下阅读。
往往这些具有输运功能的复杂网络结构系统,大家通常会通过一幅图来清晰直观的表示,例如图论的经典“哥尼斯堡七桥”问题:18世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸联系起来(如概述图)。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。
图可以清晰直观的展示出这些复杂网络结构,可是如何从数学上准确的描述一幅图呢?这需要我们了解图论的基本知识。
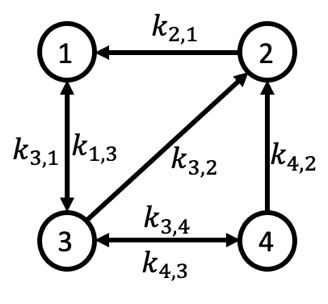
一幅图通常由两种元素构成:节点V和边E。在图1中,黑色圆点代表各个节点,节点之间的黑色连线是边,代表两个节点之间具有某种联系。如果任意点对(i,j)与(j,i)对应同一条边,则该图称为无向图,否则称为有向网络。通常节点之间联系的强弱程度通过边的权重W表示。举个例子说明,1,2,3,4节点分别是四个蓄水池,边则为对应蓄水池之间的管道,边的权重可以理解为管道的粗细或额定流量;在量子输运中,这些节点往往代表量子态,边代表允许的跃迁,权重代表跃迁速率。
2.2 图的生成树 (Spanning Tree)
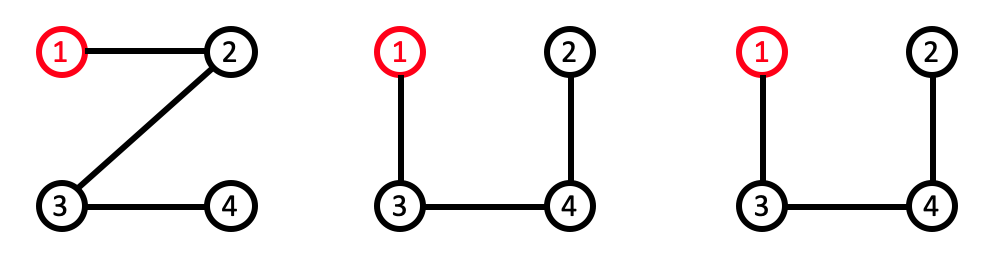
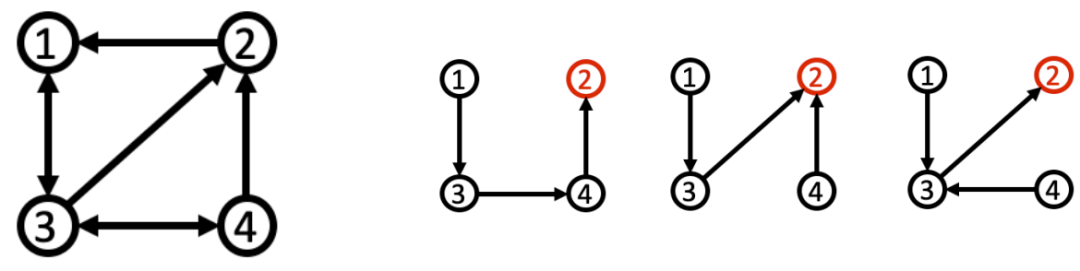
如果图G的某一子图遍历了所有节点且不含闭合回路,则该子图称为图G的生成树,且图的生成树不惟一。对于输运问题来讲,生成树对应着按不同顺序经历过所有节点的输运过程。并且从不同的顶点(称为生成树的外向根)出发进行遍历可以得到不同的生成树,甚至从同一顶点出发也可以得到不同的生成树(或者生成树中某一节点只有指入边,没有指出边,此节点称为生成树的内向根,在第三章节的讨论中若无特殊说明根均为内向根)。例如图G,从节点1出发可以得到以下三个生成树:
接下来我们将介绍描述图的一个重要矩阵:拉普拉斯矩阵。然而在介绍拉普拉斯矩阵之前,我们需要知道两个描述图特征的矩阵:度矩阵与邻接矩阵。
图G有4个节点,其度矩阵为4*4维矩阵,主对角元依次为各个节点度数,其他元素为0,图G的度矩阵D如下所示:

邻接矩阵是表示顶点之间相邻关系的矩阵。对于无向图,若节点(i,j)之间有边连接,则在矩阵i行j列和j行i列处均取值为1,若无连接则为0,对无向图而言,邻接矩阵一定是对称的,而且主对角线一定为零(在此仅讨论无向简单图),有向图则不一定如此。图G的邻接矩阵A表示如下:
其中前四项映射到图的邻接矩阵,最后一项映射到度矩阵。
在了解了图的生成树和拉普拉斯矩阵之后,本小结将介绍二者之间的关系,如何通过拉普拉斯矩阵快速计算生成树个数。与对于一幅无向图,我们可以数得对应的所有生成树个数,例如下图,共有8个生成树:

然而我们也可以通过矩阵-树定理快速计算该图生成树的数目。
矩阵-树定理(matrix-tree theorem):该定理是一个计数定理。若无向图G的拉普拉斯矩阵为L,则L的每个代数余子式相等,且等于图G的生成树的数目。这就是矩阵一树定理,我们们有时也称拉普拉斯矩阵L为基尔霍夫矩阵。对于上图G,通过矩阵-树定理计算得知其生成树数目为8 。
对于有向图也有类似的结论,例如下图,有向图G中,我们数得根在节点2上的生成树共有三个。其实这三个生成树在输运过程中代表了粒子通过不同路径,历经其它节点,最终流入节点2的三种情况。
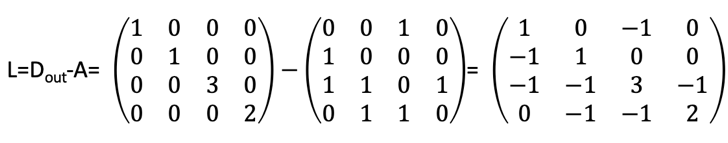 ,删除第2行和第2列求行列式,得到
,删除第2行和第2列求行列式,得到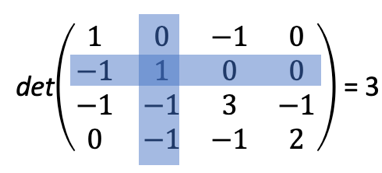 ,与我们所数结果一致。
,与我们所数结果一致。
非平衡输运可以映射到图和复杂网络结构上,如图6(a)所示,从而用圈的分解这一新视角来研究输运性质 [1]。在这里我们将介绍一个新的概念:圈流。圈流是用来衡量系统在态空间中的闭合路径(圈)上状态改变的快慢程度的物理概念,从而反能应出这条路径的活跃程度,间接体现对于整个输运过程的贡献重要程度。通过圈流大小的排序,体现了不同路径的重要程度,从而抓住主要机制,简化分析过程。
图6.(a) 非平衡输运系统映射到态空间的复杂网络。(b) 复杂网络对应的所有闭合圈轨迹。(图片来自文献[6])
非平衡驱动下的输运系统可以映射到一幅图上,例如下图G”中,系统状态映射到节点,状态改变对应于边,状态改变速率对应于边的权重:
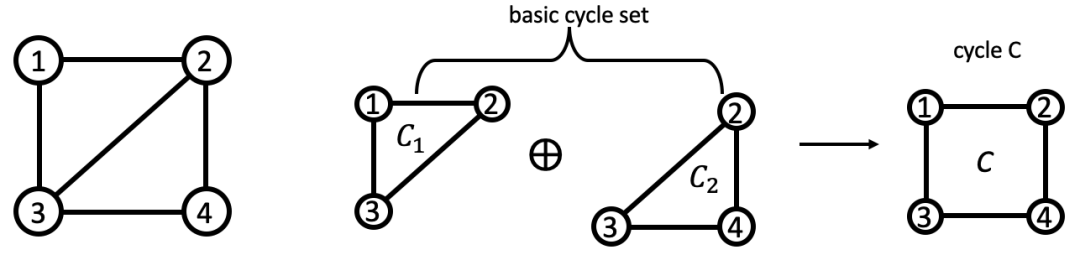
对于我们所感兴趣的功能器件或者其他动力学系统,在非平衡驱动下能保持在稳态稳定运行,这就暗含其在实空间(或者相空间、状态空间等)的运行轨迹必须是个闭合回路,即完成一个循环,否则就会在某些节点持续积累到爆炸破坏稳态。所以Schnakenberg在文献[1]中提供了一种基于网络理论中的圈分析(循环)视角研究非平衡态输运的新思路。对于图G中任何一个圈c可以通过基本圈{c1, c2, …, cν}的线性组合得到,用下面这个例子做详细说明。
在图G中,我们选定{c1, c2}作为基本圈,来得到圈c,遵循运算规则:c= ,其中
,其中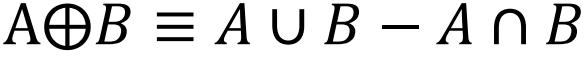 ,并且当cν中没有任意一条属于c时,ρν=0,否则ρν=1。
在圈的基础上,我们进一步介绍一个新的量:圈流。圈流的概念是由T. L. Hill在1966年的论文中[2]首次提出,并使用在生化动力学图的研究当中[3],随后Kohler在其论文[4]中进行了进一步介绍,此方法已经大量运用于生化系统动力学的研究之中。这些动力学系统常常可以通过主方程描述:
当系统到达稳态时,
,并且当cν中没有任意一条属于c时,ρν=0,否则ρν=1。
在圈的基础上,我们进一步介绍一个新的量:圈流。圈流的概念是由T. L. Hill在1966年的论文中[2]首次提出,并使用在生化动力学图的研究当中[3],随后Kohler在其论文[4]中进行了进一步介绍,此方法已经大量运用于生化系统动力学的研究之中。这些动力学系统常常可以通过主方程描述:
当系统到达稳态时,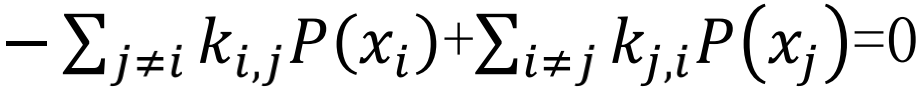 ,并且满足归一化条件:
,并且满足归一化条件: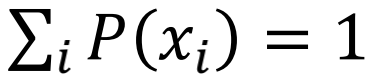 。根据克拉默法则,我们可以计算出每个状态的概率:。Hill提出了一种图论语言的方法:
。根据克拉默法则,我们可以计算出每个状态的概率:。Hill提出了一种图论语言的方法: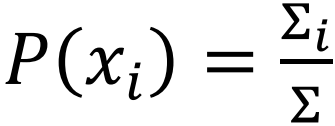 ,其中
,其中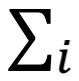 在原文中被描述为sum of directional diagrams of state i,∑在原文中被描述为sum of directional diagrams of all states。在图论中
在原文中被描述为sum of directional diagrams of state i,∑在原文中被描述为sum of directional diagrams of all states。在图论中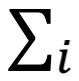 对应于所有根在节点i的生成树,先将其各自权重连乘再求和的值,其物理图像是系统最终演化到状态i的所有可能过程;∑是根在每一个节点上的所有生成树,先将其各自权重连乘在求和得到的值。根据以上描述,进一步拓展可以得到圈流的图论表达形式如下:
对应于所有根在节点i的生成树,先将其各自权重连乘再求和的值,其物理图像是系统最终演化到状态i的所有可能过程;∑是根在每一个节点上的所有生成树,先将其各自权重连乘在求和得到的值。根据以上描述,进一步拓展可以得到圈流的图论表达形式如下:
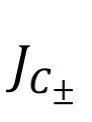 是沿圈C顺时针(+)方向或者逆时针方向(-)的圈流值,其中
是沿圈C顺时针(+)方向或者逆时针方向(-)的圈流值,其中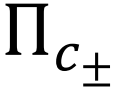 是沿圈C顺时针(+)方向或者逆时针方向(-)的权重大小。
是沿圈C顺时针(+)方向或者逆时针方向(-)的权重大小。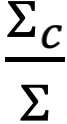 描述了系统最终演化到圈C上任何一个节点的可能性,
描述了系统最终演化到圈C上任何一个节点的可能性,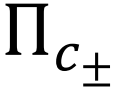 则体现为系统沿圈
则体现为系统沿圈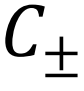 状态跃迁的速率。因此,圈流
状态跃迁的速率。因此,圈流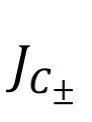 我们可以将其视为系统状态在单位时间内沿圈
我们可以将其视为系统状态在单位时间内沿圈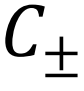 跑的圈数,即频率。
状态i与j之间的跃迁对应于图中是一条连接节点i与j的双向边。从i到j的净边流可以表达为
跑的圈数,即频率。
状态i与j之间的跃迁对应于图中是一条连接节点i与j的双向边。从i到j的净边流可以表达为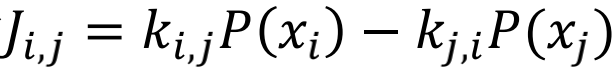 ,ki, j是从i到j的跃迁率。通过圈流,我们就可以将其进行分解对应圈流的表达
,ki, j是从i到j的跃迁率。通过圈流,我们就可以将其进行分解对应圈流的表达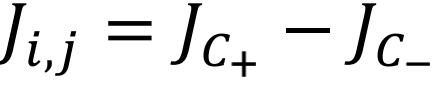 ,其中
,其中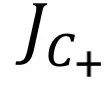 为所有包含i到j的圈流总和,
为所有包含i到j的圈流总和,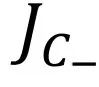 是所有包含j到i的圈流总和。例如下图中从3到2的净边流可以分解为若干个圈流的加减:
是所有包含j到i的圈流总和。例如下图中从3到2的净边流可以分解为若干个圈流的加减:

在传统研究中,我们只能局限于看到点到点的边流,通过圈流分解方法,我们就可以知道哪个圈轨迹(物理过程)对于状态i-j的跃迁,甚至于整个动力学过程起主导性作用,易于分析输运系统的主要机制。
通过以上的介绍的图论方法,我们的确可以算出每个圈的圈流,然而面临一个问题:当图变得复杂时,圈的数量会急剧增加,找出根在各个节点的生成树则变得不再具有可操作性。这时,我们则需要一个新的方法来计算圈流。在文献[5]中给出了一种新的代数图论描述,可以快速计算所有圈流的大小。
这里L是将输运系统映射到图后对应的拉普拉斯矩阵,满足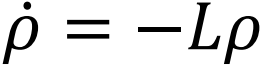 ,其中
,其中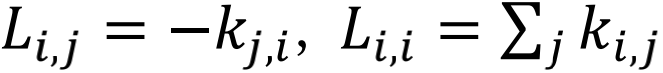 ,
,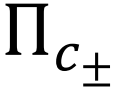 是沿
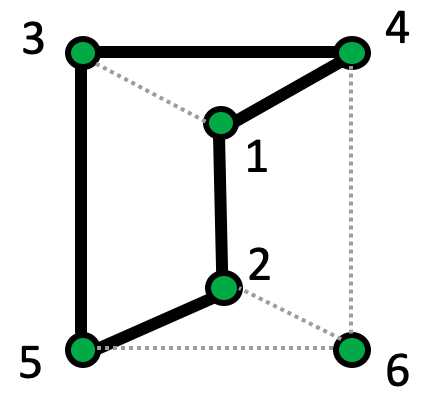
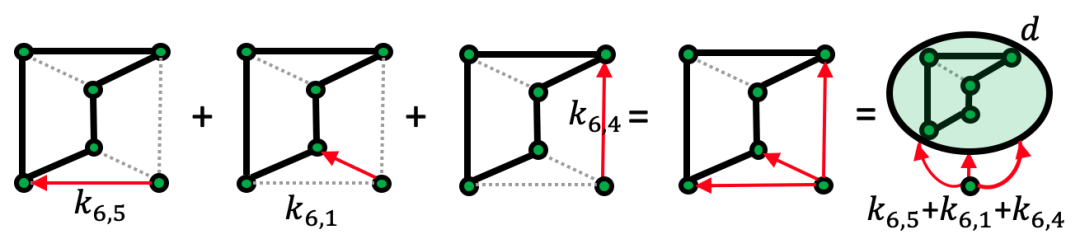
是沿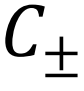 上所有跃迁率连乘,L[I,j]是指在L矩阵中划去第i行和第j列。∑c与det(L[C; C])是等价的;∑与∑idet(L[i; i]) 是等价的。关于具体推导,感兴趣的同学可以阅读钱学派的论文[7]。以下的例子将帮助我们更直观的感受。如下图所示网络结构,黑色加深边围成的路径是我们待计算的圈:
图10. 图G,黑色加深边围成的路径为我们待计算的圈。
当划去圈C所包含的{1,2,3,4,5}对应的行和列后,det(L[C;C])=∑j≠6k6, j=k6, 5+k6, 2+k6, 4,刚好对应于每一个根在圈C上的生成树的权重先连乘再求和,即∑c。这个过程也等价于将圈C捏成一个点d(图7大绿色圆形),形成一个新图,新拉普拉斯矩阵为:
删除点d后,det(L’[d;d])=∑j≠6k6, j=k6, 5+k6, 2+k6, 4,具体生成树如下图所示:
图11. ∑c与det(L[C;C])的对应关系,以及捏点之后得到新图与原图的等价关系。
上所有跃迁率连乘,L[I,j]是指在L矩阵中划去第i行和第j列。∑c与det(L[C; C])是等价的;∑与∑idet(L[i; i]) 是等价的。关于具体推导,感兴趣的同学可以阅读钱学派的论文[7]。以下的例子将帮助我们更直观的感受。如下图所示网络结构,黑色加深边围成的路径是我们待计算的圈:
图10. 图G,黑色加深边围成的路径为我们待计算的圈。
当划去圈C所包含的{1,2,3,4,5}对应的行和列后,det(L[C;C])=∑j≠6k6, j=k6, 5+k6, 2+k6, 4,刚好对应于每一个根在圈C上的生成树的权重先连乘再求和,即∑c。这个过程也等价于将圈C捏成一个点d(图7大绿色圆形),形成一个新图,新拉普拉斯矩阵为:
删除点d后,det(L’[d;d])=∑j≠6k6, j=k6, 5+k6, 2+k6, 4,具体生成树如下图所示:
图11. ∑c与det(L[C;C])的对应关系,以及捏点之后得到新图与原图的等价关系。
同济大学声子中心的任捷教授Xonics课题组聚焦于多物理场耦合体系,近期发表的工作Cycle Flux Ranking of Network Analysis in Quantum Thermal Devices,Phys. Rev. Lett. 128, 067701 (2022),通过圈流的排序的方法分析主导圈的行为特征,可以剖析多物理场耦合体系中量子热输运行为的本质,通过分析其特征来进行优化。在此工作中,通过分析与优化两个量子模型,来验证了此方法的高效性与强大。
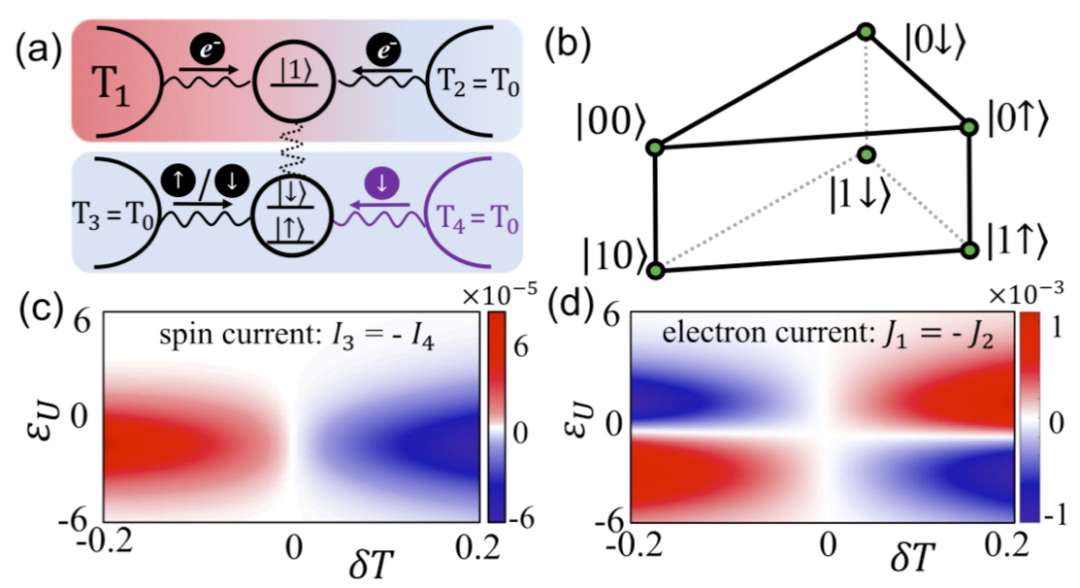
在第一个“热拖拽导致的自旋赛贝克泵浦效应”的模型中,通过此方法成果找到了主导圈的轨迹,并且论证处于平衡态子系统中的自旋流是由于热驱动产生的,而不是常见的库伦拖拽效应导致的。
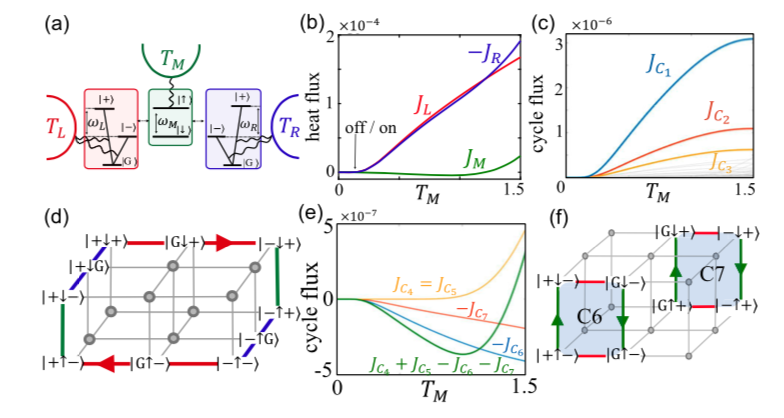
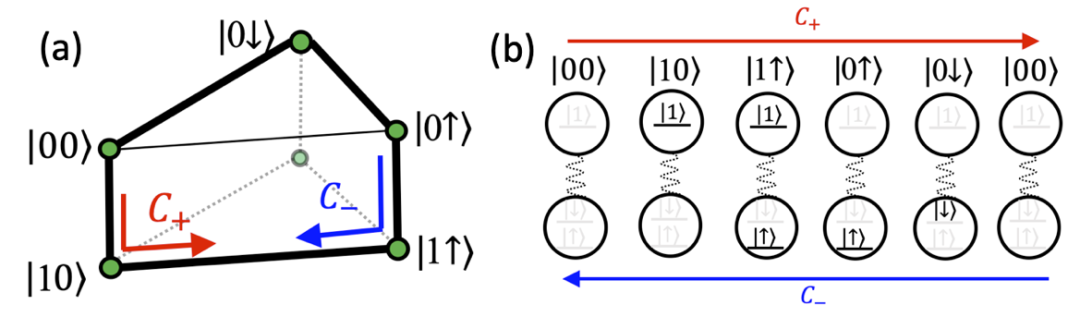
图12.(a)“热拖拽导致的自旋赛贝克泵浦”模型示意图。(b)态空间量子跃迁三棱柱。(c)(d)电流与自旋流随温差与库伦相互作用强度的变化。
图12(a)的系统是由上下两个子系统通过库伦作用耦合而成,其哈密顿量为:
上面的量子点左右耦合两个无自旋的电子库,底下的量子点左侧耦合一个有自旋的电子库,右侧耦合一个磁激子库。同时对比图12(c)(d),我们可以发现在εu≈0附近,上面子系统中的电流几乎为0,然而在下面这个没有任何非平衡力驱动的子系统中出现了明显的自旋流,并且还随着T1的温度改变而反向。这证明了处于平衡态子系统中的自旋流是由于热驱动产生的,而不是常见的库伦拖拽效应导致的。
图13.(a)主导圈轨迹C±。(b)C±逐步状态改变示意图。
进一步,通过计算圈流并且排序,我们找到了主导自旋流随温度反向的主导圈轨迹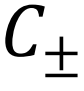 ,图13(a)。通过分析图13(b),可以得出C+提供了从左向右的自旋流,C–则提供了从右向左的自旋流,这两个圈在不同温度T1下相互竞争,从而导致了自旋流的反向,并且还进行了解析得到
,图13(a)。通过分析图13(b),可以得出C+提供了从左向右的自旋流,C–则提供了从右向左的自旋流,这两个圈在不同温度T1下相互竞争,从而导致了自旋流的反向,并且还进行了解析得到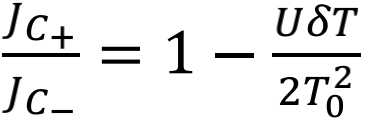 ,其大小关系是由库伦作用和温差协同决定的。
第二个“量子热晶体管”模型中如图14(a)所示,图14(b)展示了当中间端口温度超过某个阈值时,从左到右的热流受控增大的晶体管现象。作者将模型映射到状态空间得到跃迁超立方体,并在图14(c)排序展示了共16156个圈流得到主导圈,其中图14(d)中被彩色标记路径的正是主导量子热放大以及热开关的圈,并且通过其特征,反向优化了热开关的阈值位置。在图14(e)中,我们展示了负微分热导的主导圈流,并且在图14(f)中画出了其圈轨迹,仔细观察主导圈C6和C7这两个圈右状态都不变的,这表明了在此效应中,三端口模型可以基本等效为一个二端口模型,大大简化了分析。这个工作成功地将代数图论的思想引入了量子热输运领域,属于方法论上新的突破,将为未来的量子热器件设计提供新视角。
,其大小关系是由库伦作用和温差协同决定的。
第二个“量子热晶体管”模型中如图14(a)所示,图14(b)展示了当中间端口温度超过某个阈值时,从左到右的热流受控增大的晶体管现象。作者将模型映射到状态空间得到跃迁超立方体,并在图14(c)排序展示了共16156个圈流得到主导圈,其中图14(d)中被彩色标记路径的正是主导量子热放大以及热开关的圈,并且通过其特征,反向优化了热开关的阈值位置。在图14(e)中,我们展示了负微分热导的主导圈流,并且在图14(f)中画出了其圈轨迹,仔细观察主导圈C6和C7这两个圈右状态都不变的,这表明了在此效应中,三端口模型可以基本等效为一个二端口模型,大大简化了分析。这个工作成功地将代数图论的思想引入了量子热输运领域,属于方法论上新的突破,将为未来的量子热器件设计提供新视角。
图14.(a)量子热晶体管模型示意图。(b)左、中、右热流行为图。(c)圈流随中间端口温度改变行为图。(d)热放大与热开关主导圈轨迹。(e)负微分热导的主要圈流分解图。(f)主导负微分热导的圈轨迹。
[1] J. Schnakenberg, Rev. Mod. Phys. 48, 571 (1976)
[2] T. L. Hill, J. Theor. Biol. 10(3), 442 (1966).
[3] T. L. Hill and Y.-D. Chen, Proc. Natl. Acad. Sci. U.S.A. 72, 1291 (1975).
[4] H.-H. Kohler and E. Vollmerhaus, J. Math. Biol. 9, 275 (1980).
[5] J. Ren, Front. Phys. 12, 1 (2017).
[6] L. Wang, Z. Wang, C. Wang and J. Ren, Phys. Rev. Lett. 128, 067701 (2022)
[7] D.-Q. Jiang, M. Qian, and M.-P. Qian, Mathematical Theory of Nonequilibrium Steady States: On the Frontier of Probability and Dynamical Systems (Springer Science &Business Media, New York, 2004).
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「我的集智」推送论文信息。扫描下方二维码即可一键订阅:






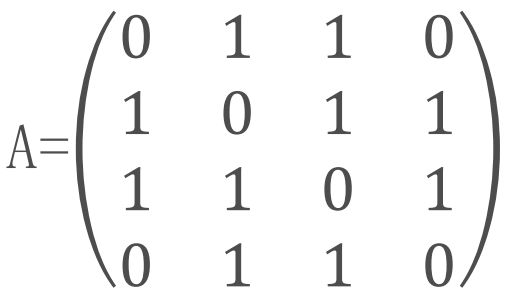



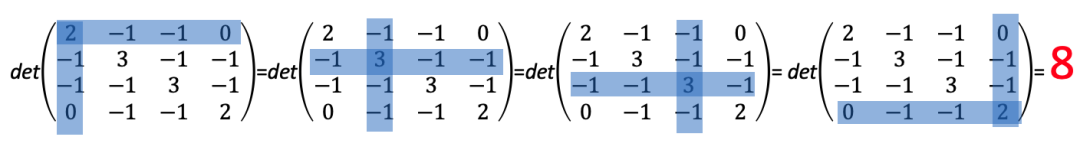
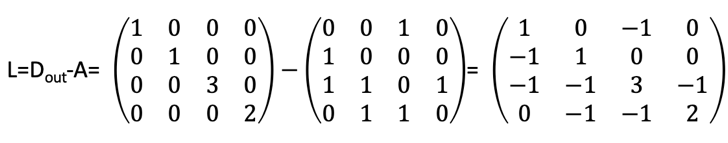 ,删除第2行和第2列求行列式,得到
,删除第2行和第2列求行列式,得到 ,与我们所数结果一致。
,与我们所数结果一致。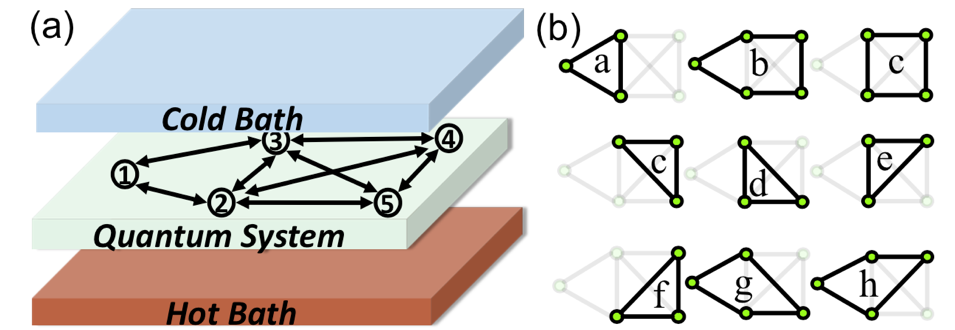
 ,其中
,其中 ,并且当cν中没有任意一条属于c时,ρν=0,否则ρν=1。
,并且当cν中没有任意一条属于c时,ρν=0,否则ρν=1。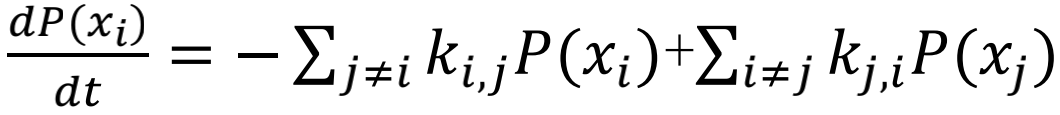
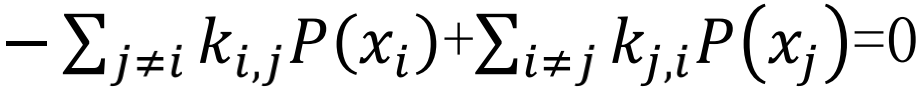 ,并且满足归一化条件:
,并且满足归一化条件: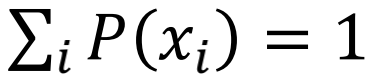 。根据克拉默法则,我们可以计算出每个状态的概率:。Hill提出了一种图论语言的方法:
。根据克拉默法则,我们可以计算出每个状态的概率:。Hill提出了一种图论语言的方法: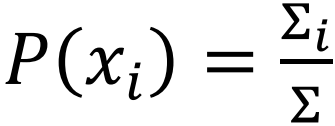 ,其中
,其中 在原文中被描述为sum of directional diagrams of state i,∑在原文中被描述为sum of directional diagrams of all states。在图论中
在原文中被描述为sum of directional diagrams of state i,∑在原文中被描述为sum of directional diagrams of all states。在图论中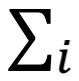 对应于所有根在节点i的生成树,先将其各自权重连乘再求和的值,其物理图像是系统最终演化到状态i的所有可能过程;∑是根在每一个节点上的所有生成树,先将其各自权重连乘在求和得到的值。根据以上描述,进一步拓展可以得到圈流的图论表达形式如下:
对应于所有根在节点i的生成树,先将其各自权重连乘再求和的值,其物理图像是系统最终演化到状态i的所有可能过程;∑是根在每一个节点上的所有生成树,先将其各自权重连乘在求和得到的值。根据以上描述,进一步拓展可以得到圈流的图论表达形式如下: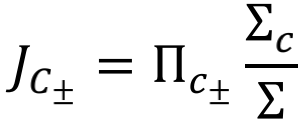
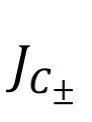 是沿圈C顺时针(+)方向或者逆时针方向(-)的圈流值,其中
是沿圈C顺时针(+)方向或者逆时针方向(-)的圈流值,其中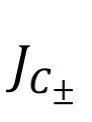 我们可以将其视为系统状态在单位时间内沿圈
我们可以将其视为系统状态在单位时间内沿圈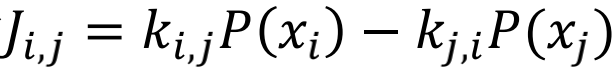 ,ki, j是从i到j的跃迁率。通过圈流,我们就可以将其进行分解对应圈流的表达
,ki, j是从i到j的跃迁率。通过圈流,我们就可以将其进行分解对应圈流的表达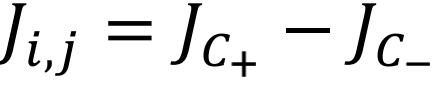 ,其中
,其中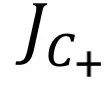 为所有包含i到j的圈流总和,
为所有包含i到j的圈流总和,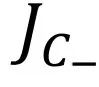 是所有包含j到i的圈流总和。例如下图中从3到2的净边流可以分解为若干个圈流的加减:
是所有包含j到i的圈流总和。例如下图中从3到2的净边流可以分解为若干个圈流的加减:
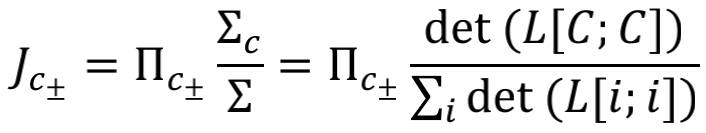
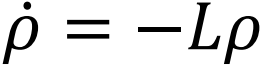 ,其中
,其中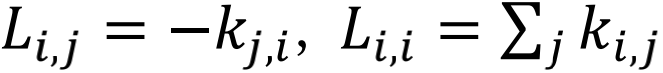 ,
,
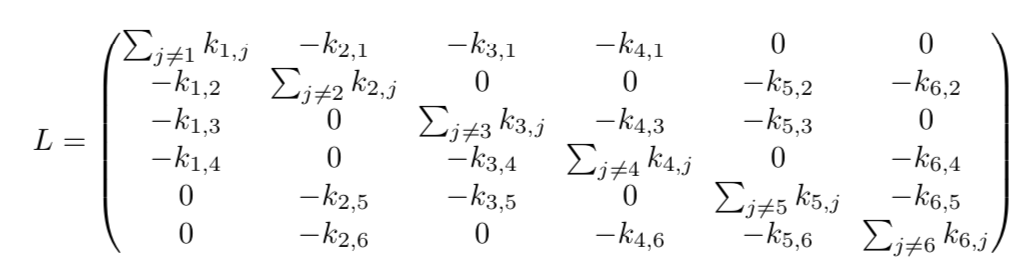
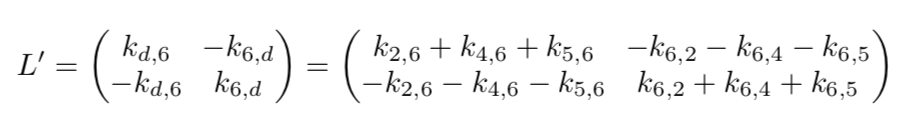

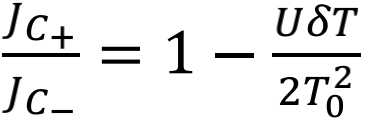 ,其大小关系是由库伦作用和温差协同决定的。
,其大小关系是由库伦作用和温差协同决定的。