PRL速递:离散度量空间的本征维数估计
2023-02-13
2,253

关键词:机器学习,数据降维,本征维数,演化
论文题目:Intrinsic Dimension Estimation for Discrete Metrics
论文来源:Physical Review Letters
论文链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.067401
真实世界中,很多数据都有离散这一特征:从分类调查到临床问卷,从未加权网络到DNA序列。然而,现有最常见的无监督降维方法是为连续空间设计的,直接用于离散空间可能会导致误差和偏差。
Physical Review Letters 这篇文章介绍了一个新算法,来估计嵌入离散空间的数据集的本征维数(intrinsic dimension, ID),利用了Ehrhart 的多面体理论。本征维数被定义为描述数据而不丢失大量信息所需的最小变量数,在无监督学习中至关重要。作者在三个不同的人工数据集上测试了该算法,并将其与著名的盒计数估计法和分形维数估计法进行比较,结果表现良好。该方法应用于分析物种指纹的宏基因组数据集,发现了该数据集的本征维数小得惊人,只有二阶。这表明:尽管序列空间是高维的,但演化压力作用在低维流形上。
图1. 本文新方法、盒计数估计法(BC)和分形维数估计法(FD)的表现
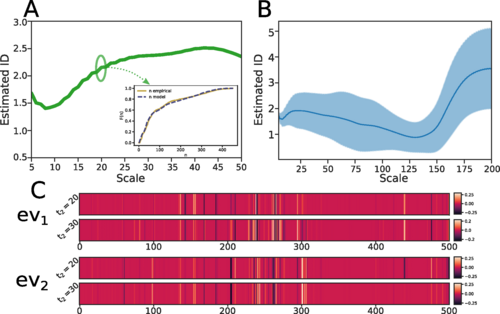
图2. 基因组学数据集簇之一的小到中等距离的本征维度估计。
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「我的集智」推送论文信息。扫描下方二维码即可一键订阅: