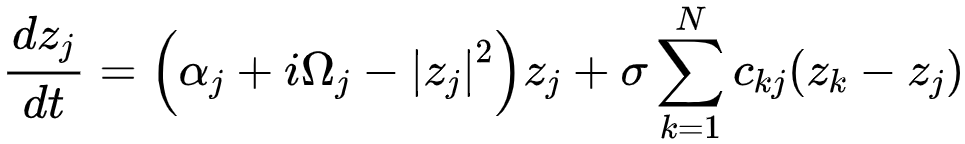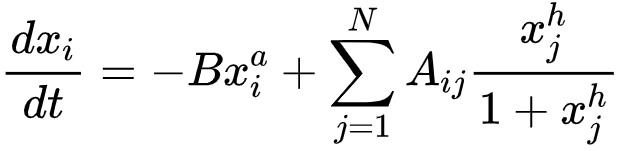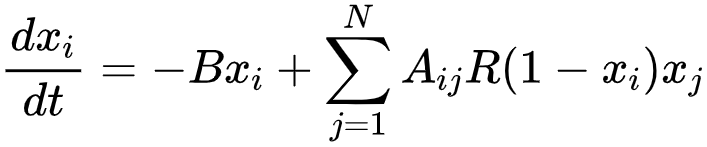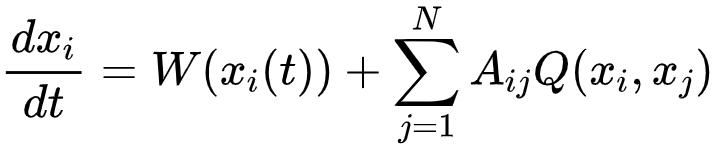许多系统一旦越过“临界点”,其状态将会发生不可逆的改变,并带来严重危害。“韧性”反映了系统避免状态转变或从非常态中快速恢复的能力,它使系统能在故障或扰动发生时调整其活动以维持基本功能。在过去50年里,人们几乎只关注低维系统韧性。随着网络科学理论的发展,学者们逐渐开始探索真实世界中复杂的多维网络系统及其韧性。2022年,Physics Reports 发表综述文章 Network Resilience 全面地回顾了网络韧性的研究方法,及其在生态、生物、社会和基础设施等复杂系统中的应用,并展望了未来网络韧性研究的方向与挑战。本文是对该综述的基础理论和方法的简介。
关键词:网络韧性,多维网络,临界转变,非线性动力学,复杂系统
https://www.sciencedirect.com/science/article/pii/S0370157322001211
1. 韧性与网络韧性
2. 网络韧性研究的核心主题
2.1 网络动力学建模
2.2 动力系统中的韧性现象
2.3 网络韧性分析工具
生活中难以预知的扰动无处不在,小到个人的感冒发烧或情绪失落,大到基础设施瘫痪或物种灭绝。考虑到扰动带来的负面后果,人们越来越关注系统应对扰动的韧性(resilience)。resilience起源于拉丁语中的 resiliere 或 resilio,分别表示“反弹”或 “回弹”[1],所以韧性又被称为弹性、恢复力等。韧性在生态、金融、交通等多个领域有着广泛应用,可以理解为系统在面对扰动事件时的反应,或系统调整其行为活动以维持基本功能的能力。虽然不同学科领域中的韧性关注点不尽相同,但各领域专业技取长补短共同推动着韧性研究的进步。
由于系统面对扰动反应的多样性和复杂性,目前仍未有韧性的统一定义。回顾过往研究里70多种韧性定义[2],大多数定义都围绕以下三类韧性:(1)系统韧性 (system resilience),又称生态韧性,主要关注系统在不转移到另一稳定状态情况下所能承受的最大扰动程度[3]。(2)工程韧性 (engineering resilience) 重点关注扰动后的恢复速率或时间[4]。(3)适应性韧性 (adaptive resilience) 多用于描述社会系统对意外和极端冲击的适应和转变能力[28]。
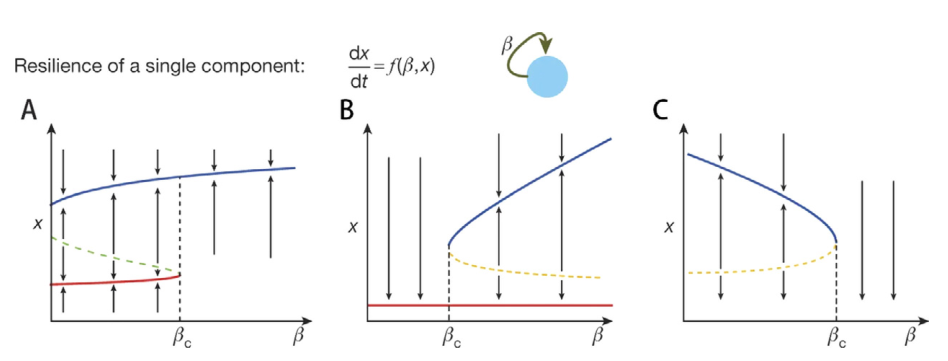
在过去几十年里,由于缺少大规模系统中的内在动力学信息和高效的分析工具,大多数研究主要集中于低维系统或时间序列数据的分析[5,6,7]。如图2所示,在动力学模型中,韧性行为可以被描述为非线性动力学方程:dx/dt=f(β, x),其中f(β, x)表示系统动力学,β表示环境状态。
图2. 一维系统的韧性。(A)当β>βc(蓝色)时,系统只有一个稳态(stable fixed point),否则会出现两个(或更多)稳态。(B)具有从积极(蓝色)状态到负面(红色)状态的一阶跃迁的韧性函数。(C)韧性函数在β<βc时有稳定解,大于βc时无解。
提取复杂系统的韧性函数需要掌握元素之间复杂相互作用的非线性动力学特征,而网络科学的出现为描述大规模真实系统中的结构提供了强有力的工具[8]。此外,海量数据和算法发展使得人们可以直接从历史数据识别并预测动态模型的准确形式[9,10]。在理论、数据和技术多方支持下,网络韧性 (network resilience) 作为分析高维系统韧性的工具应运而生。
1973年,Holling等人[11]将韧性定义为系统的持久性,及其吸收扰动和变化的能力。后来,韧性作为一个通用概念广泛应用于生物学[12]、社会科学[13]和工程学[14]中。系统韧性决定了系统是否能够容忍显著的扰动而不转移到另一个稳定状态,衡量了系统吸收状态变量、驱动变量和参数变化并保持不变的能力[15]。正如前文所介绍的,从生态学到工程学所使用的韧性传统数学处理方式为:用一维非线性动力学方程dx/dt=f(β, x)来近似复杂系统的行为,捕捉韧性相关的关键状态变化。
然而,现实世界中的系统是由许多元素通过复杂的加权有向相互作用关系组成的,并且受大量参数控制。因此它们的状态不能仅靠一维方程描述,而是需要由网络形式的耦合非线性方程来捕捉系统元素之间的相互作用关系,并揭示系统动力学和底层网络拓扑变化之间的复杂相互作用。因此 ,所得到的韧性函数是表征系统复杂参数空间上的多维流形。若要将一维系统韧性拓展到网络韧性,需要理解和回顾以下三方面内容:
(1) 网络中多维动力学方程;
(2) 高维系统的韧性现象和可能的临界转变;
2.1 网络动力学建模
网络动力学描述了网络对象的进化过程,例如一段时间内的物种丰富度如何进化[16]、个体在流行病传播过程中的感染状态[17]等等。由于该过程充满复杂性和未知性,确定其方程形式与参数并不容易。与现有的大量网络静态结构建模研究相比[18],对大规模网络动态建模的研究仍然较少。下面回顾几个经典的大规模系统的动态模型。
➢ 系统可能表现出各种非线性动力学[19,20],如振荡、扩散和分岔,这些动态模型涉及不同的方程形式和参数。例如,网络化的Stuart–Landau (SL) 振荡器系统[21]可以通过以下耦合的常微分方程 (ODEs) 来描述:
➢ 基因调控网络的动力学可以建模为米氏方程 (Michaelis–Menten equations)[22]:
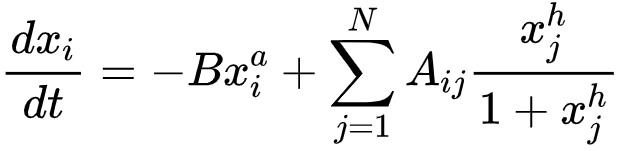
➢ 网络传播过程可以被建模为经典的SIS模型 (susceptible infected susceptible model)[23]:
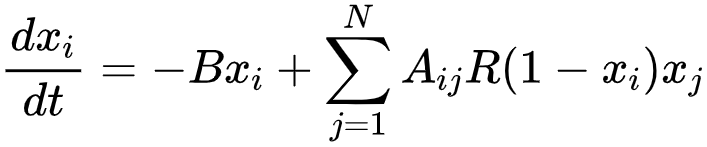
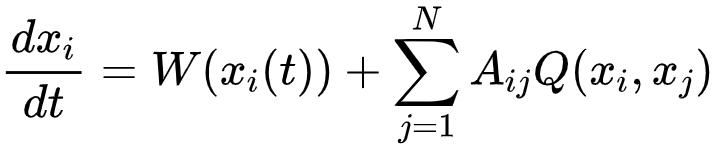
其中第一项W(xi(t))描述xi的自我驱动 (self-dynamics),第二项反映i和邻居个体的作用关系。长期以来,大规模网络的韧性预测一直受到网络内部复杂作用的限制。尽管目前对于复杂网络动力学的发现仍是一个重大挑战,但使用上述方法来推断网络动力学,有可能实现对大规模网络的动力学建模,从而构建网络韧性分析的基本框架。
2.2 动力系统中的韧性现象
动力系统的状态可能随着外部条件变化而变化,且响应通常是明显的。图3展示了不同类型的系统状态响应曲线。当外部条件随时间逐渐变化时[24],一些高韧性系统的状态可能会呈线性响应(见图3A)。更常见且更复杂的响应关系是非线性的,随着控制参数增加,出现“从上至下”连续且过渡的相变(见图3B)。在线性和连续的非线性情况下,都只存在一个平衡状态。当控制参数恢复到原先水平,系统也可以恢复到之前的状态[25,26]。一些系统可能在特定的条件范围内“反应迟钝”,而在控制参数接近某阈值时突然响应,在两个独立的状态之间表现出意想不到的状态转移(见图3C)。以上三种类型的状态变化称为相变 (phase shift) 或稳态转移 (regime shifts)。如图3D所示,一些特殊系统也会在特定的控制参数范围内产生交替稳定状态 (alternative stable states) 或多稳态 (multiple stable states)[27]。
相变在所有环境下均呈单一状态(尽管状态在阈值处可能发生变化)。交替稳定状态的存在意味着在相同环境下,至少在一定范围内可以出现两种不同的稳态,其中经常出现滞回相变 (hysteresis phase transition)。在交替稳定状态情况下,状态之间的转变表现为强烈的质变,相变情况则表现为简单的量变。
图3. 不同类型的系统状态响应曲线。(A)系统的状态对环境变化做出线性响应;(B)随着环境参数的增加,从“上”到“下”的持续状态转移;(C)两个相互排斥的稳态之间发生突然的状态转移;(D)滞回系统中在多个关键阈值处发生多稳态间的状态转移。
(1)交替稳定状态 (alternative stable states):
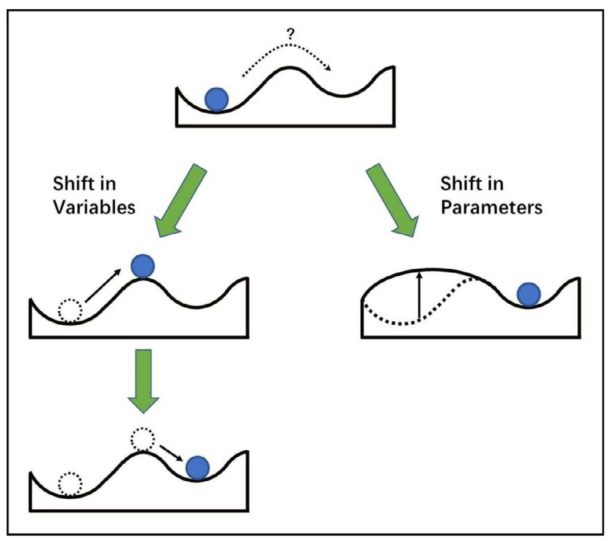
系统中的交替稳定可以用图4中的“杯中小球”来表示 [28]。若用小球位置表示系统的实际状态,在没有外界干预的情况下,小球总会向着更低的位置移动,并最终稳定在某个状态中。那如何实现小球从一个稳定状态移动至另一个稳定状态呢?方法一是改变小球的位置(如左图),即对本身状态变量进行大规模扰动。方法二是改变小球所属的环境(如右图),即改变控制动力系统内部的相互作用参数。
(2)突然相变 (abrupt phase shifts) 和临界点 (tipping points)
当外部环境或控制参数超过某一临界点时,往往会带来灾难性且不可逆的后果。因此,准确预测系统的突然相变和临界点是网络韧性的重要主题之一。具有交替稳态的状态突变通常与分岔 (bifurcation) 和突变理论(catastrophe theory)有关[29,30],如图3D所示。由于在相同的条件下很难收集到关于分岔的经验数据,从多个稳定状态中区分相变存在难度。幸运的是,尽管需要有包含许多稳态转移的大规模时间序列,但目前已有多种方法可以用来推断交替稳定状态是否涉及稳态转移[31,32,33]。
(3)临界慢化 (critical slowing down)
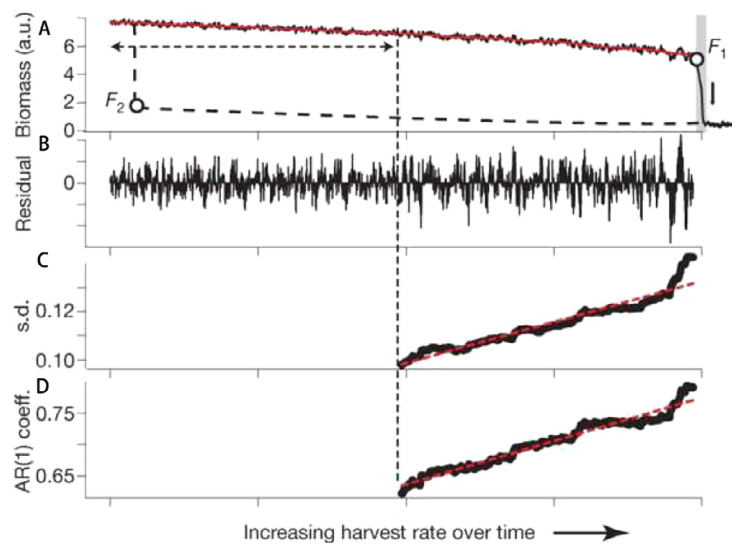
当系统接近但没有越过临界点时,可能会发生动力学系统理论中的临界慢化现象[34]。该现象表现在越接近临界点时,系统恢复到原有状态的速率会变慢、持续时间变长、恢复能力变弱。因此,一个小扰动后的恢复速率可以用来表明系统接近分岔点的程度,临界慢化现象也被用作为临界点到来的早期预警[35]。通过系统地测试恢复速率来评估临界慢化不适用于大多数真实系统,但几乎所有的真实系统都受到持续的自然扰动。当接近分岔时,临界慢化现象在系统动力学中导致三种可能的预警信号:(1)从扰动中恢复速率较慢;(2)自相关性增加(见图5);(3)方差增加[35]。自相关性和方差是临界慢化的间接度量,并且两者都预计在临界转变之前增加。
图5. 在时间序列中临界变化的早期预警信号。(A)生物量的时间序列;(B)临界变化前波动的振幅有所增加;(C)方差;(D)AR(1)模型参数估计。
综上所述,复杂网络通常以非线性和非单调的方式响应外部扰动。由于交替稳定状态的存在,即使在相同的条件下,网络也可能显示出完全不同的状态,这使得预测稳态转移或临界点极具挑战性。比较幸运的是,当系统接近临界点时,临界慢化现象及相关指标能有效地预告临界点的到来。
2.3 网络韧性分析工具
在过去的50年里,人们开发了许多分析工具来研究低维系统的韧性现象或预测临界点,这些工具大多致力于低维动力学方程的平衡分析。对于大规模网络,除了网络内部动力学变化莫测以外,缺乏合适的分析工具也制约网络韧性准确预测。
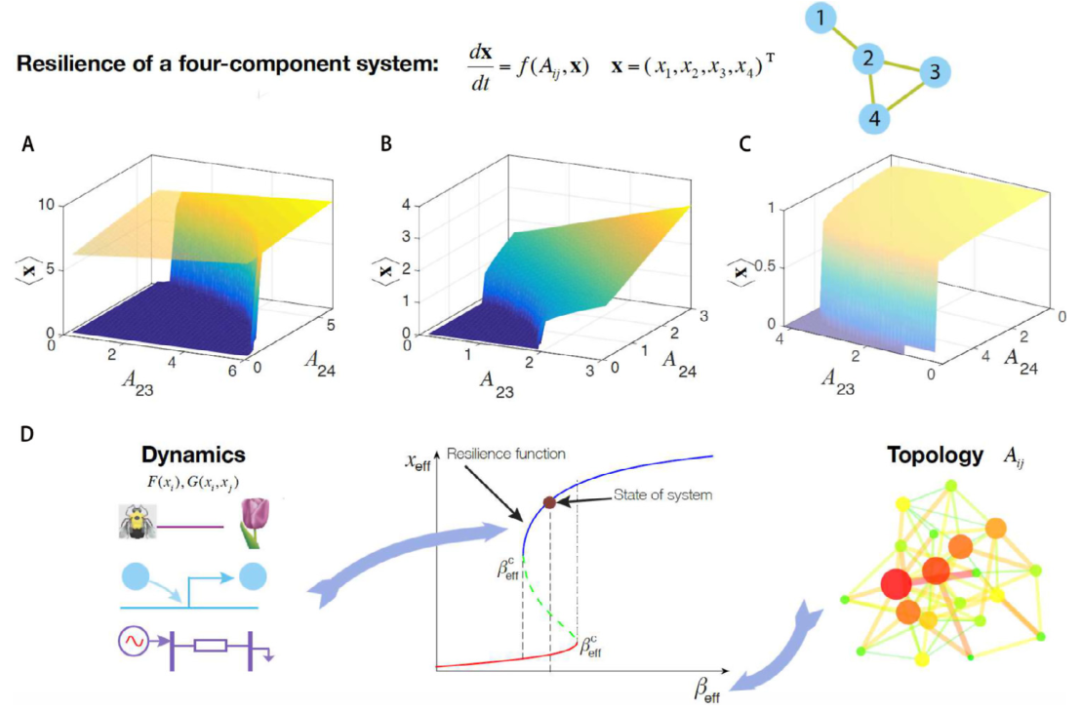
对于完整网络,Gao等人[36]最近提出一个能将高维系统动力学映射为有效的一维系统动力学的通用框架,称为GBB降维理论 (GBB reduction theory)。该模型不仅能准确预测系统对各种扰动的响应,还能准确定位系统失去韧性的临界点。这项关于复杂网络普遍韧性模式的研究提出了可能用于避免韧性失效的潜在干预策略,以及能成功应对扰动的最佳韧性系统原则。
图6. 多维系统中的网络韧性。(A)-(C)中三维图显示了四个节点系统的韧性平面;(D)采用[36]中GBB理论后,(A)-(C)中的多维流形降维成一维韧性函数。研究表明,通过将多维系统映射到β空间,可以准确预测系统的各种扰动和临界点。
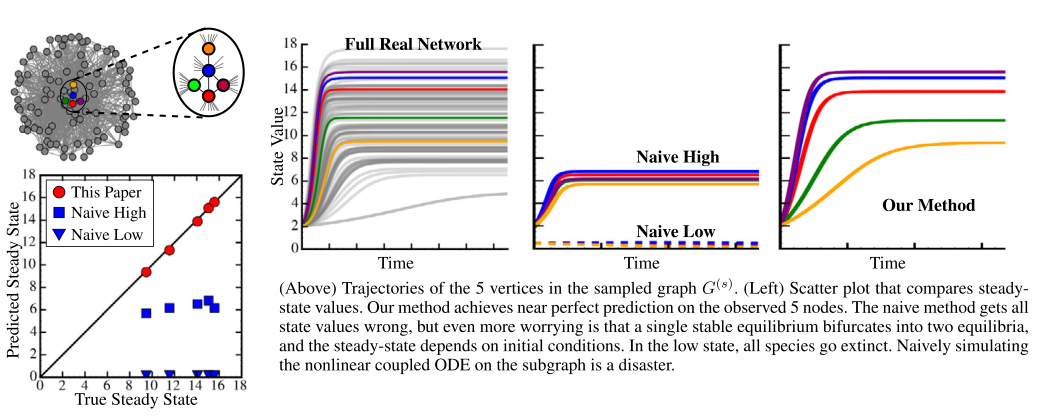
此外,如何推断不完整网络的韧性也是一个重要问题。Jiang等人[37]利用降维中的平均场方法来学习网络中部分真实稳定状态,而不需要知道整个网络信息。大多数真实网络(主要是生物和生态网络)是不完整的,这种方法可以辅助推断网络真实的动力学特征。同样,Jiang等人[38]将平均场理论和组合优化相结合,从观察到的不完整网络中推断出拓扑学特征,如度。
图7. 基于5个物种的相互作用关系,预测包含97个物种的生态网络稳态丰度[37]。
除了网络层面的韧性现象之外,每个节点对于网络韧性的贡献又如何呢?基于等价的一维模型,Zhang等人[39]提出“韧性中心性” (resilience centrality) 来量化节点对系统韧性的影响能力。韧性中心性主要由节点的度和加权最近邻度决定,该指标能帮助人们设计出有效的真实网络保护策略(如互惠网络和基础设施系统)。
2.4 三个相似概念辨析
稳定性 (stability) 和鲁棒性 (robustness) 都与韧性密切相关,它们通常用于分析系统在不断变化的条件下如何响应,有时很难区分[40]。简单来说,韧性是系统的持久性属性,稳定性表示一个系统在受到临时扰动后返回到一个特定稳态的能力,这两个概念都是在网络动力学的背景下定义的[36,3]。鲁棒性的概念通常与网络静态结构有关,它衡量的是当网络的一部分节点或边失效时,网络维持连通的能力[41]。
➢ 稳定性:stability一词来自拉丁语stabilis,意为坚定或牢靠。稳定性主要应用于生态学中[46],表示受到扰动的情况下系统保持生态功能和恢复到初始平衡状态的能力[43]。例如,对于具有交替稳定状态的系统,稳定性取决于交替稳定状态的数量——可能的稳定状态越少,系统越稳定。“韧性”集中在吸引域的边界上,而 “稳定性 “则集中在平衡状态上。一方面,一个系统可以是非常有韧性的,但存在有很大的波动,即稳定性低。另一方面,一个稳定的系统可能具有低韧性。
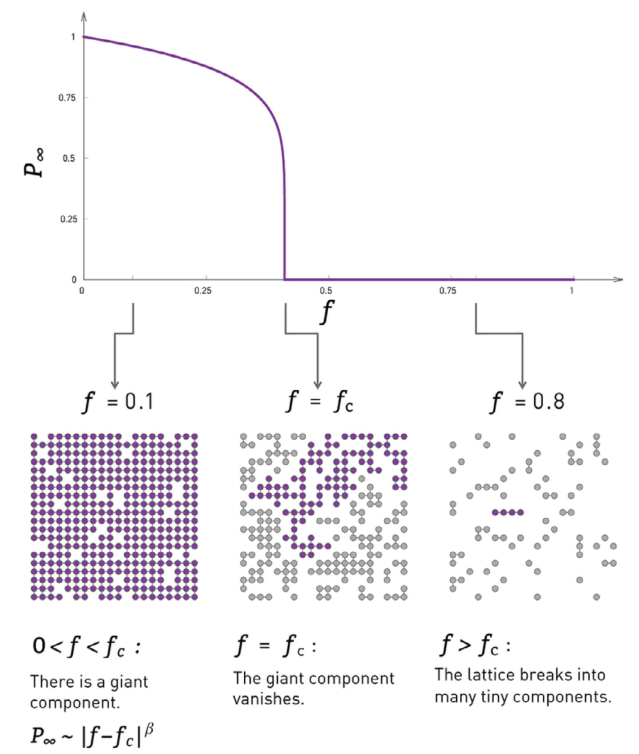
➢ 鲁棒性:robustness来源于拉丁语 quercus robur,在古代世界是力量与长寿的象征。一个系统的鲁棒性是指系统在不丧失功能的情况下承受故障和扰动的能力。例如,生物学家将鲁棒性定义为生物系统在不可预测的扰动下仍能保持特定功能的能力[44];在网络科学中,鲁棒性衡量其在一部分节点或边被破坏时保持连接的能力[45] ;在数学上,网络的鲁棒性被建模为一个反向渗流过程[46]。
图8. 网络鲁棒性可理解为随机移除部分节点后巨片的大小[47]。
韧性是描述系统受到扰动并维持其基本功能的能力,广泛应用于生物、社会、工程等多个学科领域。该综述介绍了低维系统韧性到多维网络韧性的演变,并基于大规模网络的理论工具和先进的数据分析技术,重点探讨了如相变 (phase shift)、稳态转变(regime shifts)等便于理解网络韧性的核心主题。同时,文章辨析了系统“稳定性”、“鲁棒性”和“韧性”三个常见属性的区别与关联,有利于进一步加深对网络韧性及其动力学的理解。
[1] Giliberto Capano, Jun Jie Woo, Resilience and robustness in policy design: A critical appraisal, Policy Sci. 50 (3) (2017) 399–426.
[2] Len Fisher, More than 70 ways to show resilience, Nature 518 (7537) (2015) 35.
[3] Crawford S. Holling, Resilience and stability of ecological systems, Annu. Rev. Ecol. Syst. 4 (1) (1973) 1–23.
[4] Crawford Stanley Holling, Engineering resilience versus ecological resilience, Eng. Within Ecol. Constr. 31 (1996) (1996) 32.
[5]Lei Dai, Kirill S. Korolev, Jeff Gore, Slower recovery in space before collapse of connected populations, Nature 496 (7445) (2013) 355.
[6]Marten Scheffer, Steve Carpenter, Jonathan A. Foley, Carl Folke, Brian Walker, Catastrophic shifts in ecosystems, Nature 413 (6856) (2001) 591.
[7] Marten Scheffer, Jordi Bascompte, William A. Brock, Victor Brovkin, Stephen R. Carpenter, Vasilis Dakos, Hermann Held, Egbert H. Van Nes, Max Rietkerk, George Sugihara, Early-warning signals for critical transitions, Nature 461 (7260) (2009) 53.
[8] Albert-László Barabási, Réka Albert, Emergence of scaling in random networks, Science 286 (5439) (1999) 509–512.
[9] Wen-Xu Wang, Ying-Cheng Lai, Celso Grebogi, Data based identification and prediction of nonlinear and complex dynamical systems, Phys. Rep. 644 (2016) 1–76.
[10] Baruch Barzel, Yang-Yu Liu, Albert-László Barabási, Constructing minimal models for complex system dynamics, Nature Commun. 6 (2015) 7186.
[11] Crawford S. Holling, Resilience and stability of ecological systems, Annu. Rev. Ecol. Syst. 4 (1) (1973) 1–23.
[12] Hannah R. Meredith, Virgile Andreani, Helena R. Ma, Allison J. Lopatkin, Anna J. Lee, Deverick J. Anderson, Gregory Batt, Lingchong You, Applying ecological resistance and resilience to dissect bacterial antibiotic responses, Sci. Adv. 4 (12) (2018) eaau1873.
[13] Talcott Parsons, Edward A. Shils, Neil J. Smelser, The social system, in: Toward a General Theory of Action, Routledge, 2017, pp. 190–233.
[14] Erik Hollnagel, David D. Woods, Nancy Leveson, Resilience Engineering: Concepts and Precepts, Ashgate Publishing, Ltd., 2006.
[15] Rachel J. Standish, Richard J. Hobbs, Margaret M. Mayfield, Brandon T. Bestelmeyer, Katherine N. Suding, Loretta L. Battaglia, Valerie Eviner, Christine V. Hawkes, Vicky M. Temperton, Viki A. Cramer, et al., Resilience in ecology: Abstraction, distraction, or where the action is? Biol. Cons. 177 (2014) 43–51.
[16] Igor Volkov, Jayanth R. Banavar, Stephen P. Hubbell, Amos Maritan, Neutral theory and relative species abundance in ecology, Nature 424 (6952) (2003) 1035.
[17] Maksim Kitsak, Lazaros K. Gallos, Shlomo Havlin, Fredrik Liljeros, Lev Muchnik, H. Eugene Stanley, Hernán A. Makse, Identification of influential spreaders in complex networks, Nat. Phys. 6 (11) (2010) 888.
[18] Mark E.J. Newman, The structure and function of complex networks, SIAM Rev. 45 (2) (2003) 167–256.
[19] Liming Pan, Dan Yang, Wei Wang, Shimin Cai, Tao Zhou, Ying-Cheng Lai, Phase diagrams of interacting spreading dynamics in complex networks, Phys. Rev. Res. 2 (2) (2020) 023233.
[20] Huanfei Ma, Siyang Leng, Kazuyuki Aihara, Wei Lin, Luonan Chen, Randomly distributed embedding making short-term high-dimensional data predictable, Proc. Natl. Acad. Sci. 115 (43) (2018) E9994–E10002.
[21] Gouhei Tanaka, Kai Morino, Kazuyuki Aihara, Dynamical robustness of complex biological networks, in: Mathematical Approaches to Biological
Systems, Springer, 2015, pp. 29–53.
[22] Uri Alon, An Introduction to Systems Biology: Design Principles of Biological Circuits, CRC Press, 2006.
[23] Marian Boguná, Claudio Castellano, Romualdo Pastor-Satorras, Nature of the epidemic threshold for the susceptible-infected-susceptible dynamics in networks, Phys. Rev. Lett. 111 (6) (2013) 068701.
[24] David Tilman, Joseph Fargione, Brian Wolff, Carla D’antonio, Andrew Dobson, Robert Howarth, David Schindler, William H. Schlesinger, Daniel Simberloff, Deborah Swackhamer, Forecasting agriculturally driven global environmental change, Science 292 (5515) (2001) 281–284.
[25] Peter J. Mumby, Robert S. Steneck, Alan Hastings, Evidence for and against the existence of alternate attractors on coral reefs, Oikos 122 (4) (2013) 481–491.
[26] Steve R. Dudgeon, Richard B. Aronson, John F. Bruno, William F. Precht, Phase shifts and stable states on coral reefs, Mar. Ecol. Prog. Ser. 413 (2010) 201–216.
[27] Marten Scheffer, Steve Carpenter, Jonathan A. Foley, Carl Folke, Brian Walker, Catastrophic shifts in ecosystems, Nature 413 (6856) (2001) 591.
[28] Beatrix E. Beisner, Daniel T. Haydon, Kim Cuddington, Alternative stable states in ecology, Front. Ecol. Environ. 1 (7) (2003) 376–382.
[29] Michael G. Crandall, Paul H. Rabinowitz, Bifurcation from simple eigenvalues, J. Funct. Anal. 8 (2) (1971) 321–340.
[30] Erik Christopher Zeeman, Catastrophe theory, in: Structural Stability in Physics, Springer, 1979, pp. 12–22.
[31] Stephen R. Carpenter, Alternate states of ecosystems: evidence and some implications, Ecol. Achiev. Challenge (2001) 357–383.
[32] William A. Broock, José Alexandre Scheinkman, W. Davis Dechert, Blake LeBaron, A test for independence based on the correlation dimension, Econometric Rev. 15 (3) (1996) 197–235.
[33] Stephen R. Carpenter, Michael L. Pace, Dystrophy and eutrophy in lake ecosystems: implications of fluctuating inputs, Oikos (1997) 3–14.
[34] C. Wissel, A universal law of the characteristic return time near thresholds, Oecologia 65 (1) (1984) 101–107.
[35] Marten Scheffer, Jordi Bascompte, William A. Brock, Victor Brovkin, Stephen R. Carpenter, Vasilis Dakos, Hermann Held, Egbert H. Van Nes, Max Rietkerk, George Sugihara, Early-warning signals for critical transitions, Nature 461 (7260) (2009) 53.
[36] Jianxi Gao, Baruch Barzel, Albert-László Barabási, Universal resilience patterns in complex networks, Nature 530 (7590) (2016) 307.
[37] Chunheng Jiang, Jianxi Gao, Malik Magdon-Ismail, True nonlinear dynamics from incomplete networks, in: Proceedings of the AAAI Conference on Artificial Intelligence, vol. 34, (01) 2020, pp. 131–138.
[38] Chunheng Jiang, Jianxi Gao, Malik Magdon-Ismail, Inferring degrees from incomplete networks and nonlinear dynamics, in: Christian Bessiere(Ed.), Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI-20, International Joint Conferences on Artificial Intelligence Organization, 2020, pp. 3307–3313, Main track.
[39] Yongtao Zhang, Cunqi Shao, Shibo He, Jianxi Gao, Resilience centrality in complex networks, Phys. Rev. E 101 (2) (2020) 022304.
[40] Nicolas Urruty, Delphine Tailliez-Lefebvre, Christian Huyghe, Stability, robustness, vulnerability and resilience of agricultural systems. a review, Agron. Sustain. Dev. 36 (1) (2016) 15.
[41] Réka Albert, Hawoong Jeong, Albert-László Barabási, Error and attack tolerance of complex networks, Nature 406 (6794) (2000) 378–382.
[42] Anthony R. Ives, Stephen R. Carpenter, Stability and diversity of ecosystems, Science 317 (5834) (2007) 58–62.
[43] Monica G. Turner, William H. Romme, Robert H. Gardner, Robert V. O’Neill, Timothy K. Kratz, A revised concept of landscape equilibrium: disturbance and stability on scaled landscapes, Landscape Ecol. 8 (3) (1993) 213–227.
[44] Hiroaki Kitano, Biological robustness, Nature Rev. Genet. 5 (11) (2004) 826–837.
[45] Xueming Liu, Hao Peng, Jianxi Gao, Vulnerability and controllability of networks of networks, Chaos Solitons Fractals 80 (2015) 125–138.
[46] Sergey V. Buldyrev, Roni Parshani, Gerald Paul, H. Eugene Stanley, Shlomo Havlin, Catastrophic cascade of failures in interdependent networks, Nature 464 (7291) (2010) 1025.
[47] Albert-László Barabási, et al., Network Science, Cambridge University Press, 2016.