2023年新冠疫情就结束了吗?混沌理论预测五国感染人数变化

摘要
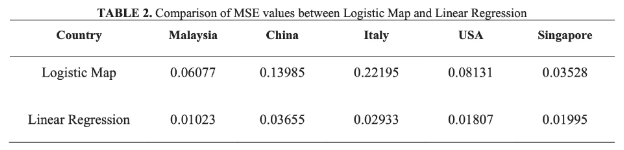
2022年发表于AIP Conference Proceedings的这篇论文使用混沌理论分析并预测COVID-19感染数量的研究。通过最大李雅普诺夫指数(LLE)对COVID-19时间序列数据中的混沌行为进行研究,并使用混沌指标工具Logistic Map预测2023年每日新增感染者的情况。研究比较了最大李雅普诺夫指数和线性回归模型的均方误差以验证Logistic Map的准确性。使用的数据源时间跨度为2020年1月底至12月初,涉及马来西亚、中国、新加坡、美国和意大利五个国家。结果显示这些国家中存在微弱的混沌行为,同时预测结果显示部分国家的感染人数在上升,部分国家的感染人数会下降。
关键词:混沌理论,最大李雅普诺夫指数,Logistic 映射,COVID-19感染人数预测

牛晓杰 | 作者
邓一雪 | 编辑

原文题目: The application of chaos theory in COVID-19 data analysis 原文链接: https://aip.scitation.org/doi/abs/10.1063/5.0093272
引言
引言
方法
方法
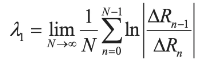
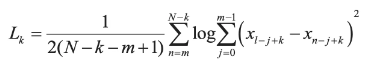
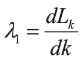
Logistic Map
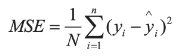
线性回归(Linear Regression)
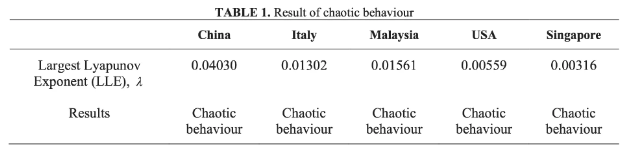
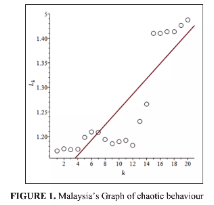
结果:探索混沌行为
结果:探索混沌行为
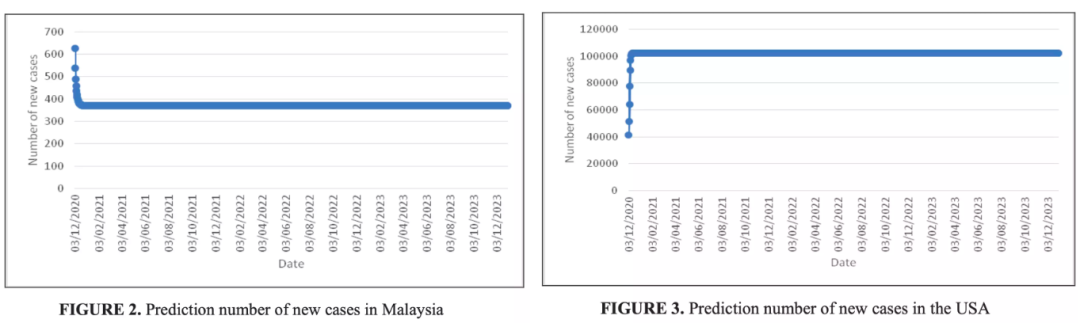
预测结果
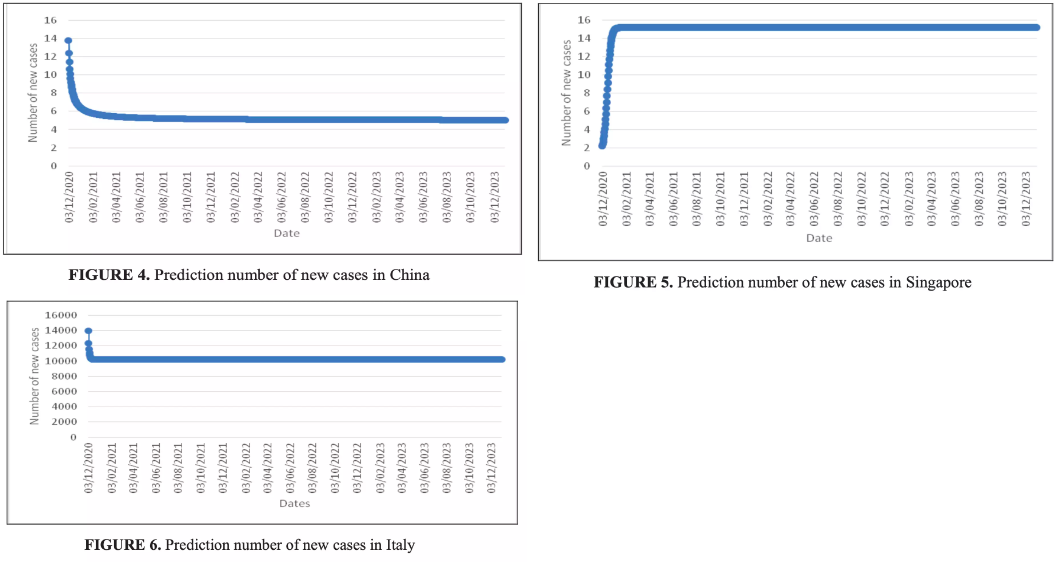
结论
结论
参考文献
课程上新:混沌科学
详情请见:
推荐阅读
-
什么是李雅普诺夫函数 | 集智百科 -
社交网络的时空动力学:疫情让我们失去了弱关系 -
口罩与疫情的博弈:为什么传染率低反而感染更多人? -
《张江·复杂科学前沿27讲》完整上线! -
成为集智VIP,解锁全站课程/读书会 -
加入集智,一起复杂!











