论文题目：Synchrony for Weak Coupling in the Complexified Kuramoto Model

论文来源：Physical Review Letters

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.187201

同步（Synchrony）指两个或两个以上随时间变化的量在变化过程中保持一定的相对关系，协调事件以统一地操作一个系统。在物理系统中表示：两个或几个随时间变化的量，在变化过程中保持一定的相对关系。

Kuramoto 模型是典型的振子同步模型，描述了一大类弱耦合强吸引极限环振子。我们一般用平均场序参量r（r∈[0,1]，r=1代表所有单元都同步）来量化Kuramoto模型的同步。当K>K^pl（经典锁相临界耦合强度）时，同步以锁相状态（phase-locked states，即任意两变量之差恒为常数）出现；而当K=K^pl时，不存在锁相状态；当K→0时，平均场序参量r=ο(N^p-1/2)。

然而，对这个看似简单的模型进行了近半个世纪的研究，仍有几个基本问题尚未解决。比如，对有限尺度的系统，关于非相干态和部分锁定态的稳定性的重要方面仍然没有得到解决，关于非相干态（incoherent）和部分锁相状态（partially locked states）的稳定性的本质问题仍然没有解决。

最近发表在 Physical Review Letters 的这篇文章从一个新视角出发，解析地分析了有限尺度的复变量 Kuramoto 模型。他们发现对于强耦合（如实变量系统），锁定状态（locked states）构成吸引子，从而涌现出同步。然而，当耦合强度K＜K^pl时，同步仍以复杂锁定状态（complex locked states）的形式持续存在。稳定的复杂锁定状态表示在实变量模型中零平均频率的闭锁亚群（locked subpopulation），并且它们的虚部有助于识别构成该亚群的元素。他们还发现了在K＜K^pl处会出现二次跃迁，此时，复杂锁定状态变得线性不稳定，但对于任意小的耦合强度K，同步仍然存在。

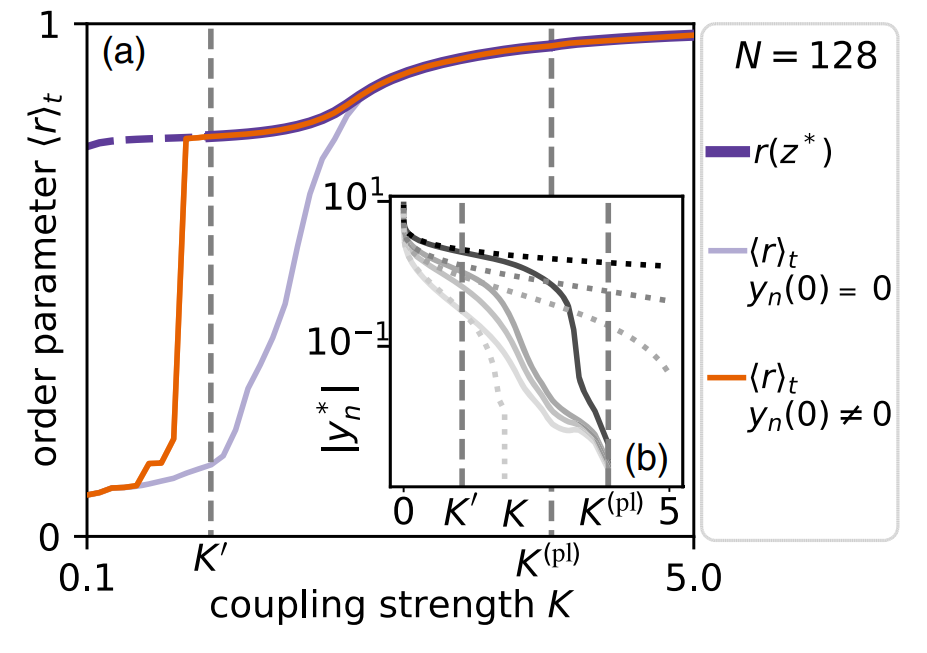
图1. 弱耦合区的同步

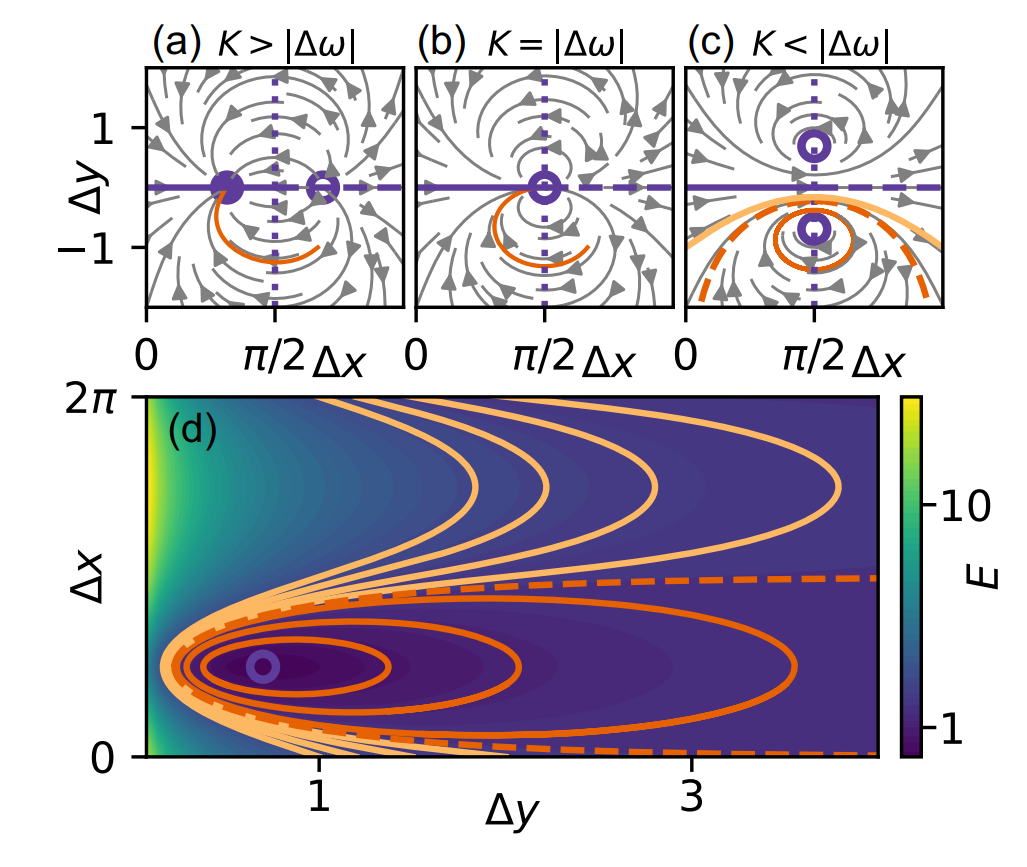
图2. N=2时的复杂锁定状态。

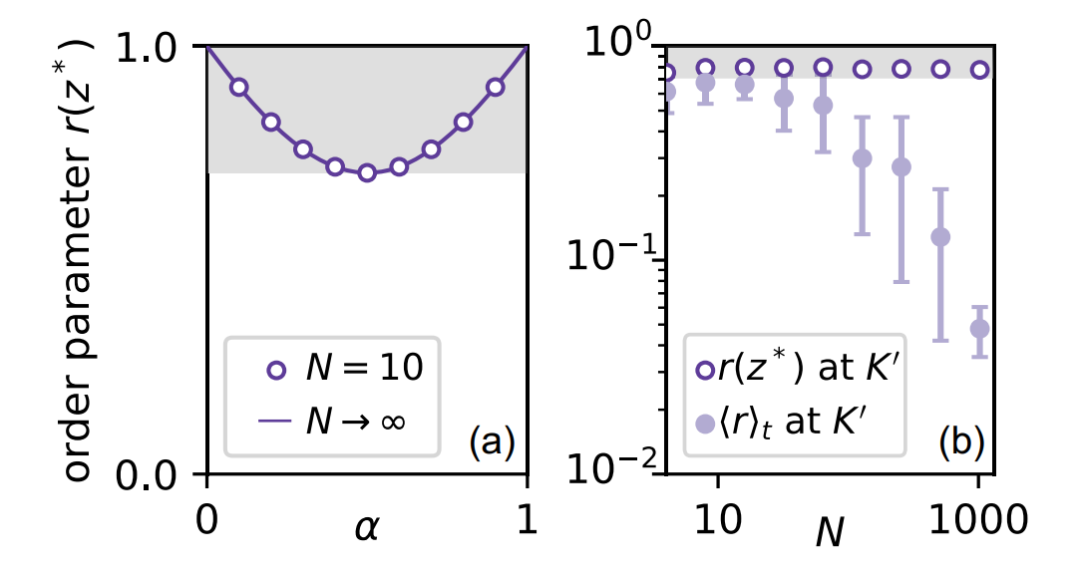
图3. N增加时的持续复合同步。

推荐阅读