Nat. Commun. 速递:分岔行为塑造连续物理动力学如何解决离散的伊辛优化问题

关键词:离散组合优化,非线性动力学,物理启发优化方法,分岔理论


论文题目:Bifurcation behaviors shape how continuous physical dynamics solves discrete Ising optimization 论文来源:Nature Communications
论文链接:https://www.nature.com/articles/s41467-023-37695-3
二次无约束二值优化问题(Quadratic Unconstrained Binary Optimization, QUBO)对很多学科都非常重要,包括系统药物设计、分子动力学模拟、蛋白质折叠、交通流优化、工作调度和金融风险分析等等。解决 QUBO 问题被证明是NP难问题(NP-hard),限制了良好解决方案的可扩展性,即使是近似的算法也是数百到数千个变量的数量级。
模拟物理动力学来解决困难的组合优化问题已被证明对中到大规模问题有效。这种系统的动力学是连续的,不能保证找到原始离散问题的最优解。这篇发表于 Nature Communications 的文章,研究了模拟物理求解器何时能正确解决离散优化这一开放性问题,重点是相干伊辛机(coherent Ising machines, CIM,又称量子神经网络计算机)。在建立了相干伊辛机动力学和离散伊辛优化之间的精确映射之后,论文展示了伊辛动力学在第一个分岔点的两种根本不同的分岔行为:要么所有节点状态同时偏离零(同步分岔),要么经历级联偏离(迟滞分岔)。
对于同步分岔,研究证明,当节点状态在远离原点的地方均匀受限时,它们包含足够的信息来精确解决伊辛问题。当确切的映射条件被违反时,随后的分岔就变得很有必要,并且常常导致缓慢的收敛。受这些发现的启发,作者设计了一种捕获和校正 (trapping-and-correction, TAC)技术来加速基于动力学的伊辛求解器,包括相干伊辛机和模拟分岔。捕获和校正利用早期分岔的“陷阱节点”,在整个伊辛动力学过程中保持其符号,以有效地减少计算时间。通过使用公开基准和随机伊辛模型的问题实例,最后验证了捕获和校正技术的卓越收敛性和准确性。这些结果提供了关于连续物理动力学和离散组合优化之间联系的重要见解,并可能推动增强的非线性和物理启发优化方法的参数控制方案。
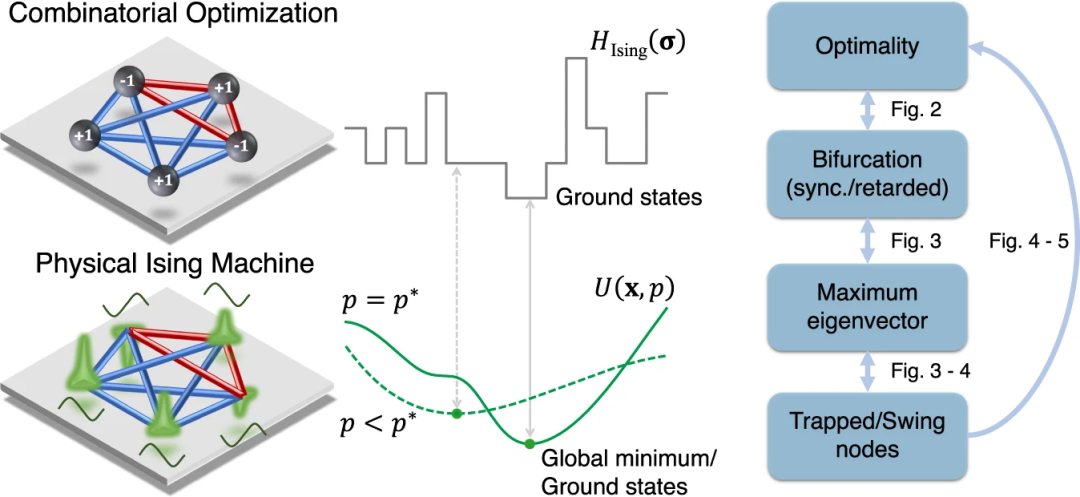
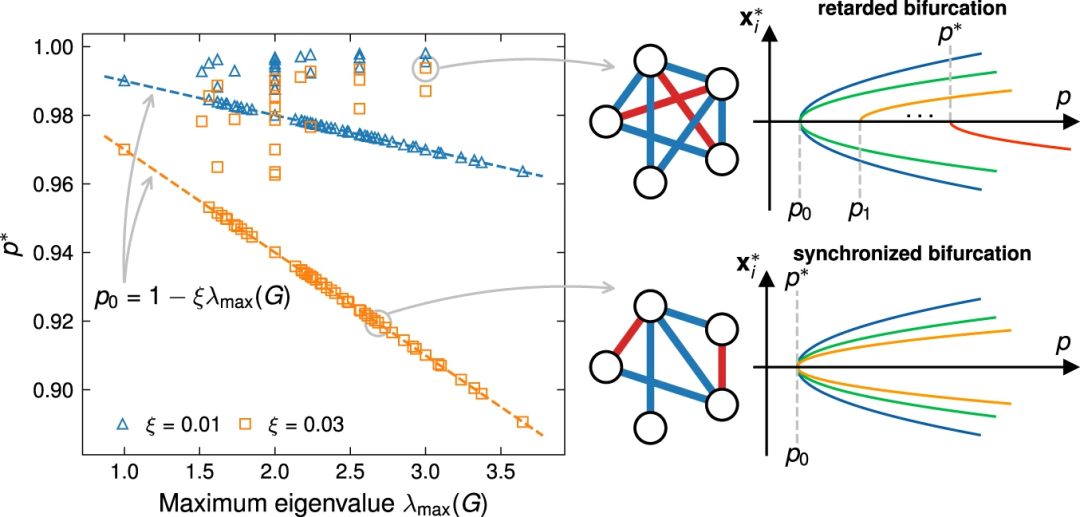
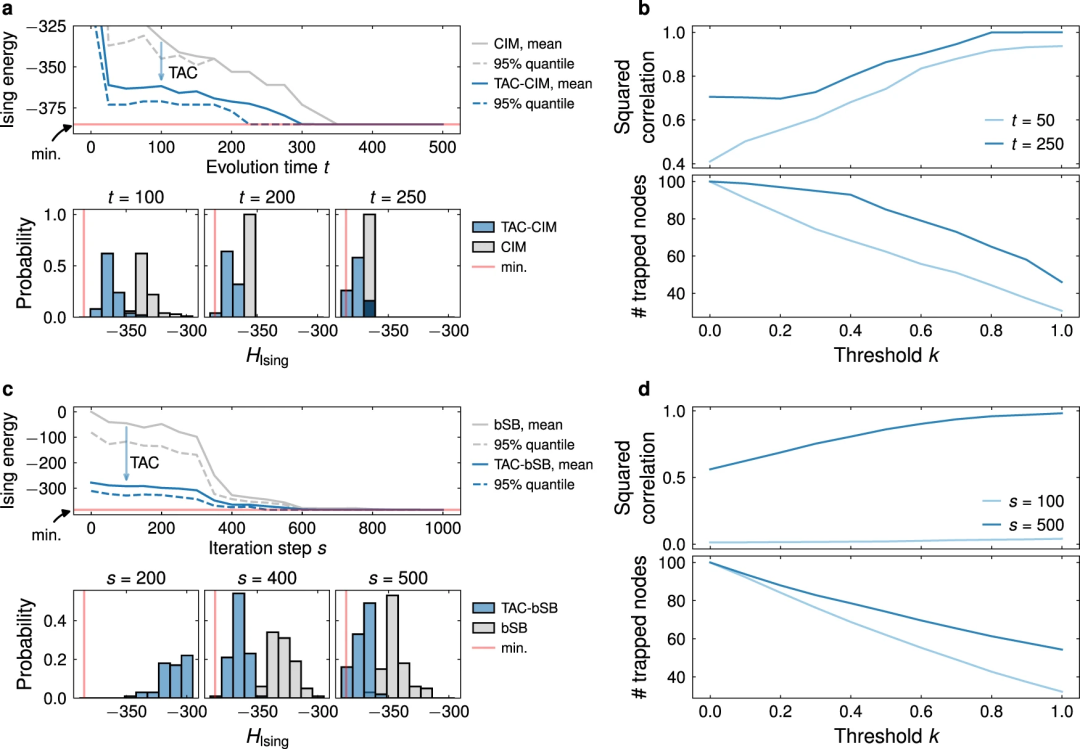
图3. 通过捕获和校正 (TAC) 技术加速基于动力学的伊辛机
图神经网络与组合优化读书会

推荐阅读










