大模型热潮之后的未来新方向：图神经网络与组合优化 | 文献汇总

导语

现实世界中大量问题的解决依赖于算法的设计与求解。传统算法由人类专家设计，而随着人工智能技术不断发展，算法自动学习算法的案例日益增多，如以神经网络为代表的的人工智能算法，这是算法神经化求解的缘由。在算法神经化求解方向上，图神经网络是一个强有力的工具，能够充分利用图结构的特性，实现对高复杂度算法的高效近似求解。基于图神经网络的复杂系统优化与控制将会是大模型热潮之后新的未来方向。

为了探讨图神经网络在算法神经化求解的发展与现实应用，集智俱乐部联合国防科技大学系统工程学院副教授范长俊、中国人民大学高瓴人工智能学院助理教授黄文炳，共同发起「图神经网络与组合优化」读书会。读书会将聚焦于图神经网络与算法神经化求解的相关领域，包括神经算法推理、组合优化问题求解、几何图神经网络，以及算法神经化求解在 AI for Science 中的应用等方面，希望为参与者提供一个学术交流平台，激发参与者的学术兴趣，进一步推动相关领域的研究和应用发展。读书会从2023年6月14日开始，每周三晚 19:00-21:00 举行，持续时间预计8周。欢迎感兴趣的朋友报名参与！

读书会框架介绍

过去几年，随着神经网络和深度学习技术的快速发展，图神经网络用于组合优化问题的求解已经取得了显著进步，尤其是在端到端求解、局部改进求解以及处理自然输入等方面。

同时，算法推理技术的出现让深度学习模型模仿经典算法，实现了传统算法的泛化性和神经网络的最优解的完美结合。此外，图神经网络的出现还极大推动了AI在基础科学中的应用，实现了人工智能与基础学科的深度融合，从而极大地促进了相关学科的发展。

本次读书会旨在分享这些领域的最新研究成果，以促进图神经网络和算法神经化求解的研究和应用的进一步发展。

以下是由两位发起人老师推荐的文献列表。

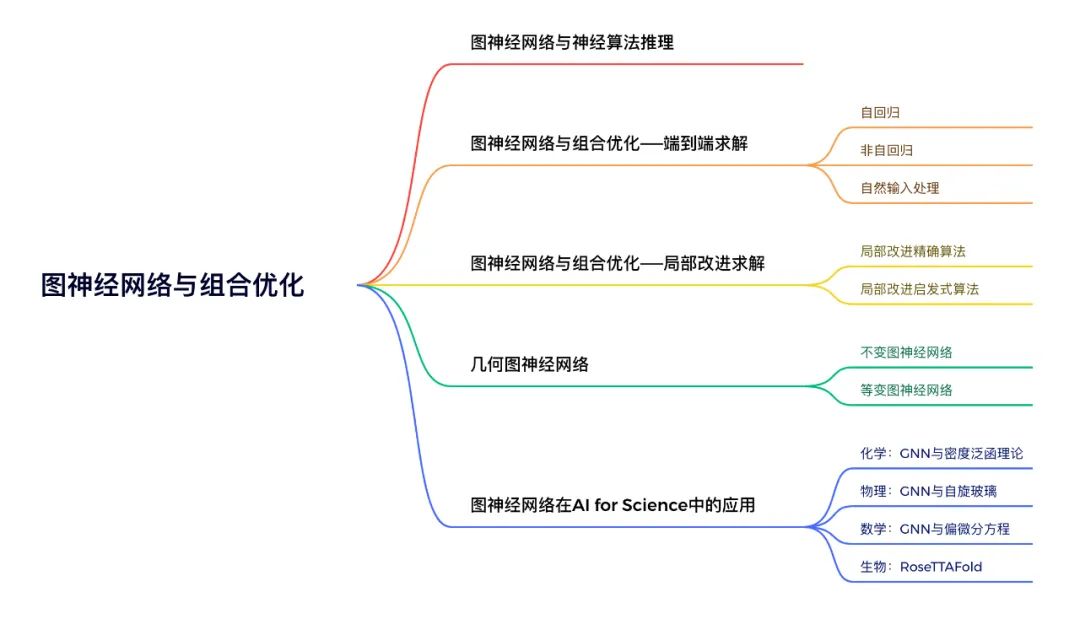
读书会文献汇总

主题一：图神经网络与经典算法对齐

简介

DeepMind提出的神经算法推理技术能够将经典算法用深度学习模型进行模仿，并实现了传统算法的泛化性和神经网络的最优解的完美结合。该技术采用算法对齐的思想，即将算法划分成多个部分，每个部分由神经算法建模。在此基础上，提出了新的GNN架构和训练机制，可有效解决复杂的组合优化问题，同时提高算法的泛化能力。

主要参考文献

Veličković P, Blundell C. Neural algorithmic reasoning[J]. Patterns, 2021, 2(7): 100273.

这篇文章提出神经算法推理的概念，通过用深度学习方法更好地模仿算法，让深度学习实现算法的高度可泛化性，同时保留对问题的最优解。

Neural Execution of Graph Algorithms. Yiding Feng, Chelsea Finn, and Stefanie Jegelka. NeurIPS 2019.

这篇文章提出了一种基于图神经网络的图算法执行框架，旨在直接对图算法进行执行而非预测。它将算法操作（如遍历）作为操作和查询节点的一部分，使用图神经网络来学习如何执行这些操作。

K. Xu, J. Li, M. Zhang, S. S. Du, K.-I. Kawarabayashi, and S. Jegelka. What can neural networks reason about? In International Conference on Learning Representations, 2020b.

这篇文章引入了算法对齐的概念，这一概念构成了神经算法推理的核心思想。

Deac A I, Veličković P, Milinkovic O, et al. Neural algorithmic reasoners are implicit planners[J]. Advances in Neural Information Processing Systems, 2021, 34: 15529-15542.

这篇文章以隐式的方式介绍了基于GNN的算法推理框架，具有较好的泛化性能。

Ibarz B, Kurin V, Papamakarios G, et al. A generalist neural algorithmic learner[C]. Learning on Graphs Conference. PMLR, 2022: 2: 1-2: 23.

这篇文章提出一个通用的神经算法推理器，该模型依赖单一参数集的GNN，能够同时学习诸如排序、搜索、贪心算法、动态规划、图算法、字符串排序和几何算法等经典算法任务，并且达到专家模型的平均水平。

主题二：图神经网络与组合优化——端到端求解

简介：图神经网络端到端求解组合优化问题的方式主要有两种：自回归和非自回归。这里有一篇关于面向组合优化问题的图学习综述文章可以提前学习一下。

1. 自回归简介

自回归方式是指在图神经网络中，将解的生成过程建模为一个逐步生成的过程。每一步生成一个解的一部分，并使用已生成的部分来指导下一步的生成。这种方式的优点是可以在生成过程中动态地考虑约束条件和优化目标，但缺点是生成速度相对较慢。

主要参考文献

Khalil E, Dai H, Zhang Y, et al. Learning combinatorial optimization algorithms over graphs[J]. Advances in neural information processing systems, 2017, 30.

这篇文章探讨了组合优化问题的一般形式，提出了一种使用自回归方式学习图上组合优化问题的求解算法。

Fan C, Zeng L, Sun Y, et al. Finding key players in complex networks through deep reinforcement learning[J]. Nature machine intelligence, 2020, 2(6): 317-324.

这篇文章提出基于深度强化学习框架，该框架可以在小型网络上进行训练，以理解复杂网络系统的组织原则，从而帮助我们设计更加抗攻击和抗故障的网络。

视频资料推荐：利用强化学习寻找复杂系统的关键节点，范长俊

https://campus.swarma.org/course/1808

Bello I, Pham H, Le Q V, et al. Neural combinatorial optimization with reinforcement learning[J]. arXiv preprint arXiv:1611.09940, 2016.

这篇文章基于自回归的方式采用强化学习求解组合优化问题，将整个问题的求解过程分解为多个步骤，并设计了一个可以自适应调整生成顺序的网络结构。

Amos B, Kolter J Z. Optnet: Differentiable optimization as a layer in neural networks[C]//International Conference on Machine Learning. PMLR, 2017: 136-145.

这篇文章提出一种新的神经网络架构，将优化问题作为单独的layer集成到更大的端到端可训练的深度网络中。

Kool W, Van Hoof H, Welling M. Attention, learn to solve routing problems![J]. arXiv preprint arXiv:1803.08475, 2018.

该论文提出了一种基于注意力机制的图神经网络架构，用于解决路由问题。该方法能够有效地学习路由问题的结构特征，并在测试集上取得了优异的性能。

视频资料推荐：注意力模型学习求解路径问题，牟牧云

https://campus.swarma.org/course/1052

2. 非自回归简介

非自回归方式是指在图神经网络中，将整个问题的求解过程作为一个整体进行求解，一次性输出最终的解。这种方式的优点是求解速度较快，但缺点是不能动态地考虑约束条件和优化目标。

主要参考文献

Li Z, Chen Q, Koltun V. Combinatorial optimization with graph convolutional networks and guided tree search[J]. Advances in neural information processing systems, 2018, 31.

这篇论文主要介绍了一种结合图卷积网络（GCN）和引导树搜索（Guided Tree Search）的组合优化算法，用于解决包括旅行商问题（TSP）和车辆路径问题（VRP）等一系列NP难问题。该算法使用GCN模型来从图形输入中提取特征，并将其输入到引导树搜索中，引导树搜索使用GCN模型提供的启发式信息来指导搜索过程。

视频资料推荐：结合图卷积网络的组合优化和树搜索，刘晶

https://campus.swarma.org/course/1086

Fu Z H, Qiu K B, Zha H. Generalize a small pre-trained model to arbitrarily large tsp instances[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2021, 35(8): 7474- 7482.

这篇文章尝试采用监督学习方式，训练一个小规模的模型，利用图采样、图转换以及热图合并等一系列技术，构建可重复用于任意规模TSP实例的热图。此外，通过输入热图到强化学习方法(蒙特卡洛树搜索)，以指导搜索高质量的解决方案。

Nazari M, Oroojlooy A, Snyder L, et al. Reinforcement learning for solving the vehicle routing problem[J]. Advances in neural information processing systems, 2018, 31.

这篇文章采用图卷积神经网络和强化学习来解决车辆路径问题。

Chalumeau F, Coulon I, Cappart Q, et al. Seapearl: A constraint programming solver guided by reinforcement learning[C]//Integration of Constraint Programming, Artificial Intelligence, and Operations Research: 18th International Conference, CPAIOR 2021, Vienna, Austria, July 5–8, 2021, Proceedings 18. Springer International Publishing, 2021: 392-409.

这篇文章将约束满足问题（CSP）建模成简单的、无向的三部图。在该图上，每个变量、可能的取值和约束都用节点表示。当且仅当一个变量涉及到一个约束，或者当一个值在一个变量的可选取值集合中时，相应的节点才由一条边连接。

Pogančić M V, Paulus A, Musil V, et al. Differentiation of blackbox combinatorial solvers[C]//International Conference on Learning Representations. 2020.

图神经网络在处理自然输入等上游任务中发挥着重要作用，可直接从自然输入如图片、语音和文本等中提取特征，并应用于组合优化问题的求解。这篇论文模型的自然输入为图片，利用神经网络解决TSP、最短路径等组合优化问题。

主题三：图神经网络与组合优化——局部改进求解

简介

图神经网络采用局部改进求解组合优化问题主要包括两种方式，一种是改进精确算法，如分支定界法中的分支用分类学习代替；另一种则是局部改进启发式算法，如改进模拟退火中的退火机制。

1. 局部改进精确算法

主要参考文献

Gasse M, Chételat D, Ferroni N, et al. Exact combinatorial optimization with graph convolutional neural networks[J]. Advances in neural information processing systems, 2019, 32.

这篇文章将MILP问题的变量和约束建模成二部图，基于建模的二部图，采用GCN和模仿学习改进分支策略。

Khalil E, Le Bodic P, Song L, et al. Learning to branch in mixed integer programming[C]. Proceedings of the AAAI Conference on Artificial Intelligence. 2016, 30(1).

这篇论文将图神经网络应用于决策树的分支选择，从而改进了传统的分支策略，从而解决混合整数规划（MIP）问题。
Chen X Y, Tian Y D. Learning to perform local rewriting for combinatorial optimization. In: Proceedings of the 33rd Conference on Neural Information Processing Systems. Vancouver, Canada: Curran Associates, Inc., 2019. 6278−6289

这篇文章提出了一个基于深度强化学习的组合优化问题搜索模型 NeuRewriter, 它和局部搜索具有相似的算法流程, 即首先随机构造一个可行解, 在该初始解的基础上通过局部搜索不断提高解的质量。

2. 局部改进启发式算法

主要参考文献

Mills K, Ronagh P, Tamblyn I. Finding the ground state of spin Hamiltonians with reinforcement learning[J]. Nature Machine Intelligence, 2020, 2(9): 509-517.

这篇文章采用强化学习方法改进模拟退火中的退火机制。

Deudon M, Cournut P, Lacoste A, et al. Learning heuristics for the tsp by policy gradient[C]//Integration of Constraint Programming, Artificial Intelligence, and Operations Research: 15th International Conference, CPAIOR 2018, Delft, The Netherlands, June 26–29, 2018, Proceedings 15. Springer International Publishing, 2018: 170-181.

神经网络框架被扩展到TSP问题上，该框架的求解效果优于高性能的启发式算法。

Xin L, Song W, Cao Z, et al. NeuroLKH: Combining deep learning model with Lin- Kernighan-Helsgaun heuristic for solving the traveling salesman problem[J]. Advances in Neural Information Processing Systems, 2021, 34: 7472-7483.

这篇文章采用GCN对节点特征进行编码，结合LKH启发式算法，能够在保证算法效率的同时，进一步提高求解精度。

主题四：几何图神经网络

简介：无论是微观世界中的分子、蛋白质、抗体、RNA，还是宏观世界中的机械系统、不同形状的物体等，构成了一类重要的数据形态——几何图。与社交网络中的拓扑图不同，几何图中的节点占据了一定的空间位置，需要满足某些内蕴的物理性质，比如对称性，导致传统的图神经网络难以处理几何图。

近年来，不变和等变图神经网络考虑了对称性，具有良好的解释性、泛化性和通用性，能有效实现几何图的处理和分析。几何图神经网络在物理系统模拟、蛋白质折叠预测（如主题五中的RoseTTAFold论文）、抗体设计（如主题五中的MEAN论文）等问题上得到了成功应用。

1. 不变图神经网络

将数据映射到某个不变特征，使得原始数据无论做任何变换，不变特征均不受影响。

K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko, and K.-R. Müller. SchNet – A deep learning architecture for molecules and materials. J.Chem.Phys 2018.

简称Schnet，早期的不变图神经网络。

Johannes Gasteiger, Janek Groß, Stephan Günnemann. Directional Message Passing for Molecular Graphs. ICLR 2020.

简称DimNet，在GNN引入了带方向的消息传播。

Johannes Gasteiger, Florian Becker, Stephan Günnemann. GemNet: Universal Directional Graph Neural Networks for Molecules. NeurIPS 2021.

简称GemNet，一种不变GNN，考虑了球面坐标，效果值得信赖。由DimNet的主要作者打造。

2. 等变图神经网络

对模型输入做一定的变换之后，模型输出做同样的变换。

Nathaniel Thomas, Tess Smidt, Steven Kearnes, Lusann Yang, Li Li, Kai Kohlhoff, Patrick Riley. Tensor field networks: Rotation- and translation-equivariant neural networks for 3D point clouds. 2018.

这篇论文简称张量场网络TFN，是最早同时满足旋转、平移等变的GNN，在分子动力模拟上进行验证，领域必读文章。

Victor Garcia Satorras, Emiel Hoogeboom, Max Welling. E(n) Equivariant Graph Neural Networks. ICML 2021.

瞩目的EGNN，目前被广泛使用的等变图神经网络模型，领域必读文章。

Johannes Brandstetter, Rob Hesselink, Elise van der Pol, Erik J Bekkers, Max Welling. Geometric and Physical Quantities Improve E(3) Equivariant Message Passing. ICLR 2022.

简称SEGNN，在EGNN基础上引入了higer-degree 不可约表示，基于这篇文章可以概括性学习E3不变表示相关知识。

主题五：图神经网络在科学计算中的应用

简介

中国科学院院士鄂维南教授提出基础学科发展新的曙光：AI for Science将人工智能与基础科学深度融合。科学领域的许多问题本质上是对物理系统的处理和分析，而物理系统是可以建模成图谱。因此，图神经网络是AI for Science领域的基础工具，极大推动了AI在分子动力学模拟、材料设计、药物发现等任务上的应用前景。

主要参考文献

数学（GNN与偏微分方程，PDE）

Iakovlev V, Heinonen M, Lähdesmäki H. Learning continuous-time pdes from sparse data with graph neural networks[J]. arXiv preprint arXiv:2006.08956, 2020.

物理（GNN与spin glasss）

Fan C, Shen M, Nussinov Z, et al. Searching for spin glass ground states through deep reinforcement learning[J]. Nature Communications, 2023, 14(1): 725.

解读文章：Nat. Commun. 前沿：深度强化学习搜索自旋玻璃基态

化学

Tian Xie, Jeffrey C. Grossman. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Physical Review Letters, 2018.

简称CGCNN，最早的晶体性质预测工作，提出multi-graph来建模晶体周期性

生物

Wang J, Ma A, Chang Y, et al. scGNN is a novel graph neural network framework for single-cell RNA-Seq analyses[J]. Nature communications, 2021, 12(1): 1882.

使用图神经网络形式化和聚合细胞-细胞关系，并使用左截断混合高斯模型对异质性基因表达模式进行建模，成功应用到单细胞RNA测序（scRNA-Seq）任务。

Minkyung Baek, Frank DiMaio, et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science, 2021.

简称RoseTTAFold，解决了蛋白质折叠问题。

Xiangzhe Kong, Wenbing Huang, Yang Liu. Conditional Antibody Design as 3D Equivariant Graph Translation. ICLR, 2023.

简称MEAN，使用了等变图神经网络完成抗体CDR区域1D氨基酸序列和3D结构的同时生成和优化。