Bianconi 新作：超图上的渗流理论

关键词：高阶网络，渗流理论，因子图，超图

论文题目：The theory of percolation on hypergraphs

论文来源：arxiv

论文链接：https://arxiv.org/abs/2305.12297

在数学中，超图（hypergraph）是一种广义上的图，是有限集合中最一般的离散结构，它的一条边（edge）可以连接任意数量的顶点（ vertex）。因为它能捕捉多个节点的交互，所以在意见动力学、流行病传播、同步和博弈的背景下引起了极大关注。尽管一些工作已经解决了超图的鲁棒性问题，但仍然缺乏超图上的超边和节点渗流理论。

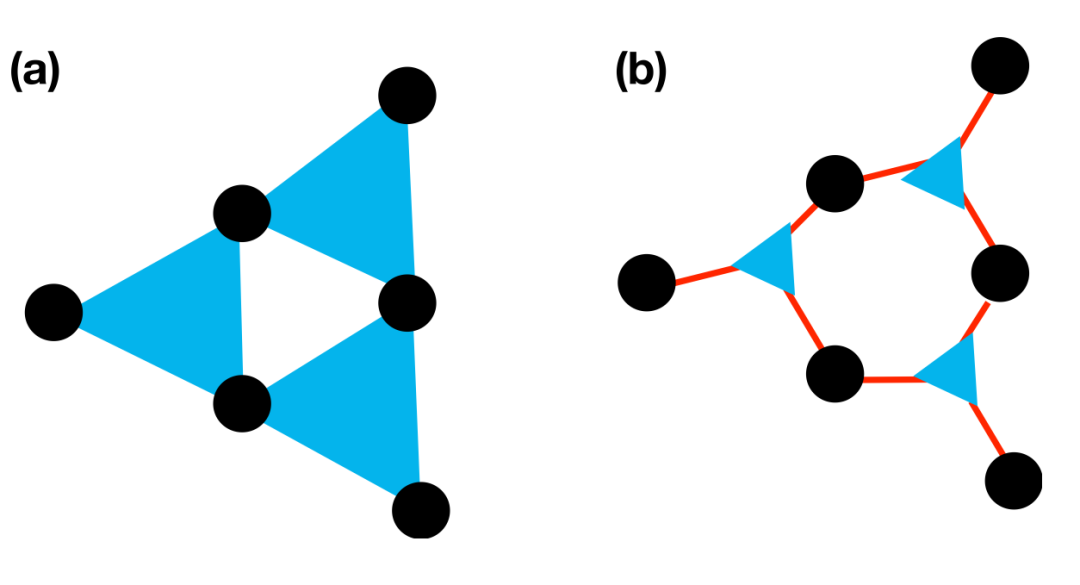
超图的超边（hyperedges）可以看作是第二类节点——因子节点（factor nodes），因此超图等价于因子图（factor graphs），因子图是基于原节点和因子节点的二分网络。因为对二分网络的研究已很充分，所以用因子图来处理超图很直接也很方便。然而在随机瓦解网络时（随机去除节点），这种直接等价就出现了问题，这是因为从超图中移除节点与从因子图中移除节点有不同的影响。

最近 Bianconi 等人发表于arxiv上的一篇最新论文专注于研究超图对随机瓦解的鲁棒性。为了证明超图上的渗流（percolation）和因子图上的渗流之间的差异，他们探讨了超图上的渗流，并将其与因子图上的渗流进行比较。

他们的方法建立在信息传递理论的渗流，推导了因子图和超图上渗流的消息传递方程，并将其应用于随机超图（random hypergraph）和随机多重超图（randommultiplex hypergraph）。随机超图模型描述了两个给定的分布：节点的度分布（degree distribution）和超边的基数分布（cardinality distribution）；随机多重超图模型描述给定的联合度分布。对于这两类随机的、局部树型超图，他们得到了渗流簇（percolation cluster，巨连通分量）的存在标准和相对大小。

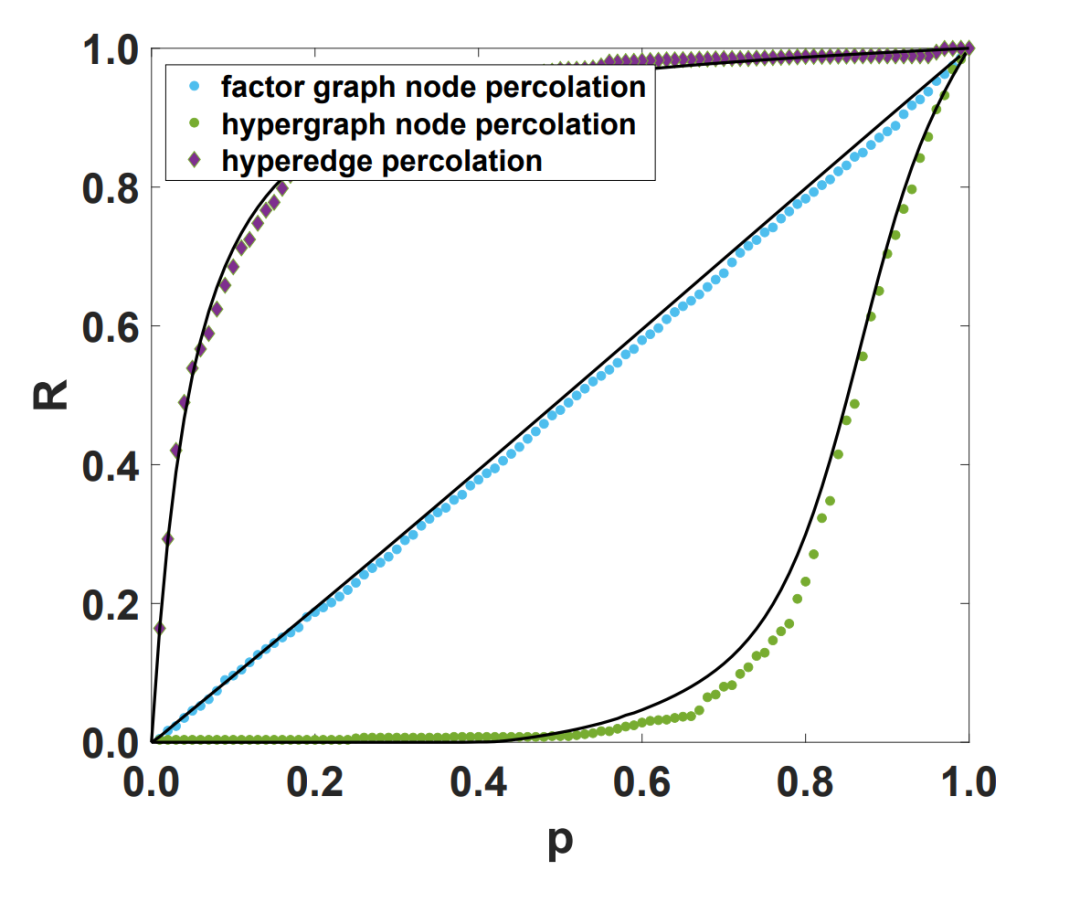
他们的结果表明：超图上的节点渗流阈值大于因子图上的节点渗流阈值；而且与普通图不同，超图的节点渗流阈值与超边渗流阈值不一致，节点渗流阈值大于超边渗流阈值。在相同的近似下，他们还分析预测了相图（phase diagram）和随机超图、随机多重超图中超图渗流的临界性质，并用蒙特卡洛模拟对结果进行了验证。