关键词:复杂网络,动力系统,小世界网络,反应扩散方程,图灵斑图
论文题目:Emergence of Geometric Turing Patterns in Complex Networks
斑图链接:https://pattern.swarma.org/paper/54f03d06-1158-11ee-a1a8-0242ac17000d
1952年,图灵创造性地使用反应-扩散系统的数学模型来描述自然界中的斑图,比如虎纹、豹斑、胚胎形态发生。这类可以用反应-扩散方程描述的斑图,被后人称为图灵斑图(Turing Pattern)。图灵斑图产生于相互竞争的扩散粒子之间的相互作用,长期以来一直是描述自然界非平衡自组织的一个重要概念,并在许多化学和生物系统中得到了广泛研究。
反应扩散系统:在文中指由两种元素组成,它们之间具有化学反应,而每一种元素也同时存在随机扩散的系统,数学上通常使用偏微分方程描述。
自组织理论:通过起源于初始无序系统的部分元素之间的局部发生相互作用,使某种形式的整体秩序形成的过程。当有足够的能量可用时,该过程可以是自发的,不需要任何外部主体进行控制。混沌理论中讨论的自组织,就如同不可预测的大海中的确定性孤岛。
历史上,人们曾在拓展系统(extended systems)和晶格(lattices)中研究过图灵斑图。但些研究中描述的网络模型并不适合描述真实的系统。很多图灵斑图(如胚胎形态发生)应在多细胞网络(multicellular network)而非连续介质(continuous medium)中研究。这种复杂的网络结构让图灵斑图的动力学研究变得困难,常局限在小型网络。
Nakao和Mikhailov在网络科学的背景下证明:在随机图中,激活-抑制类扩散系统中存在图灵不稳定性(Turing instability)。而图灵不稳定性以及相应的涌现斑图同实际网络中的度异质性密切相关,本质上是纯拓扑的。现在,人们发现,即使在缺乏明显几何组织的无标度/小世界网络中,图灵不稳定性也会产生拓扑斑图。
虽然在简单的网络模型(如WS网络)中已经发现了明确的几何斑图的线索,但在异构复杂网络中几何图灵斑图的确切性质和形态问题仍未解决。
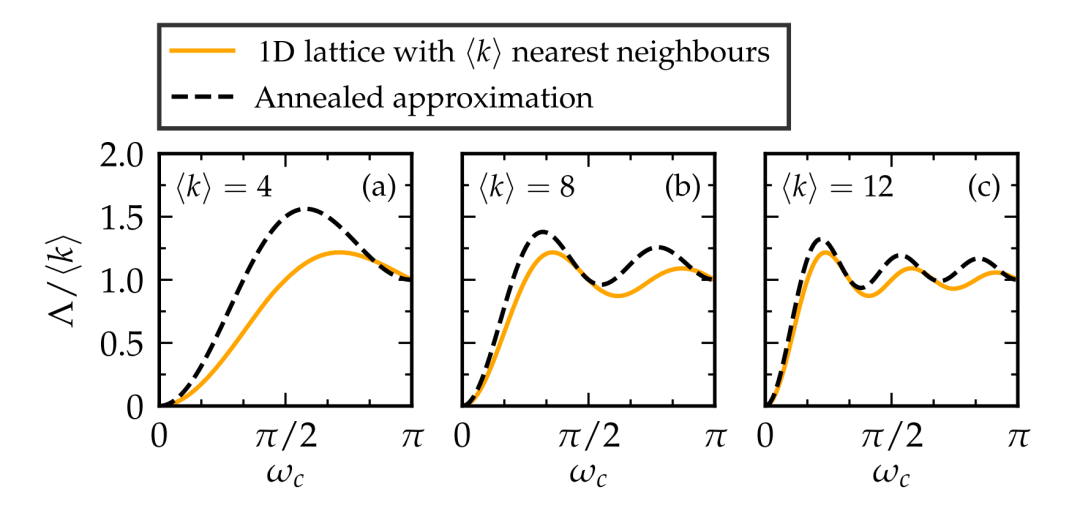
近期发表于PHYSICAL REVIEW X的这项工作研究了几何随机图模型(geometric random graph models)框架中的图灵不稳定性,用一个底层的几何空间来解释网络拓扑。此框架通过研究退火图拉普拉斯矩阵(annealed graph Laplacian)的特征向量,不仅可以观测到几何斑图,而且可以估计出它们的波长。
最后,他们还证明了可以在真实网络的几何嵌入中找到图灵斑图。这些结果表明:网络的功能与其隐藏的几何结构之间存在着深刻的联系,即使相关的动力学过程完全由网络拓扑决定。
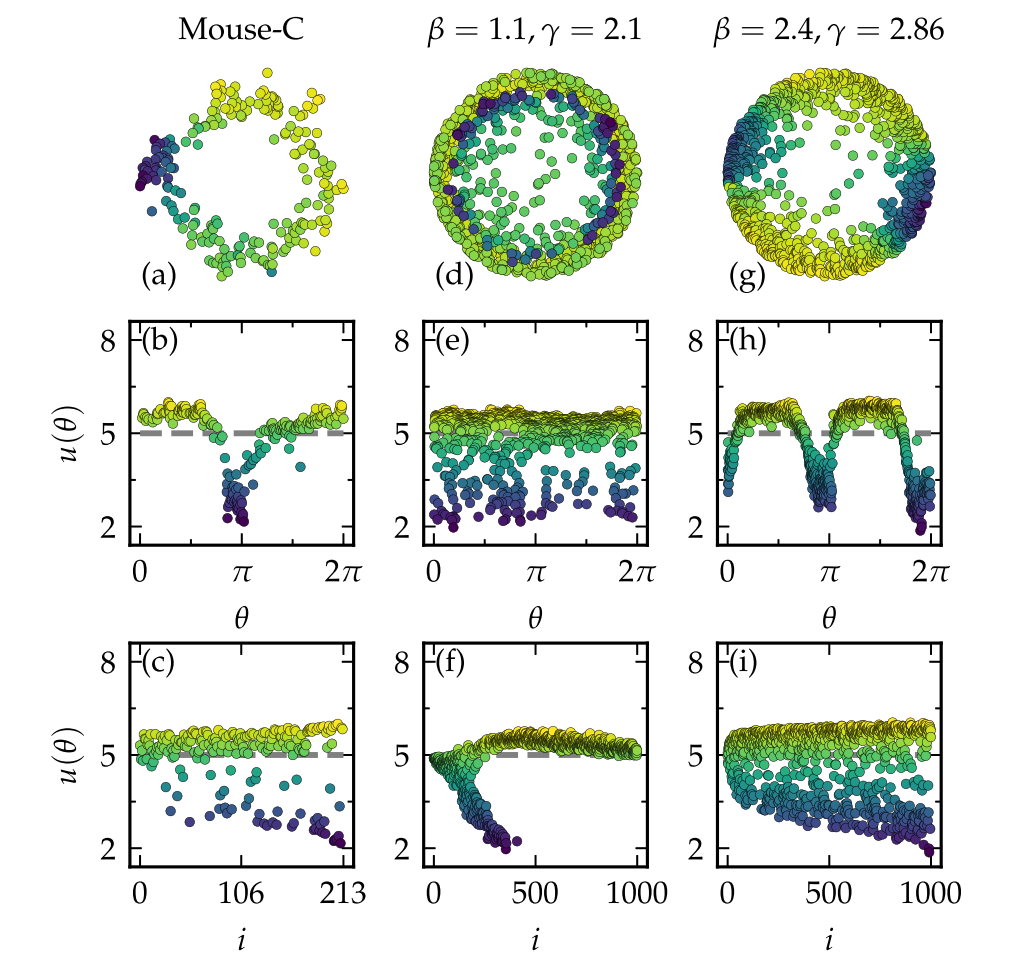
图1. 网络中图灵斑图的例子;第一列:小鼠连接组网络;第二列:强异构的S1H2模型(一种几何软配置模型);第三列:弱异构的S1H2模型。第一行:节点在双曲空间的定位;第二行:激活物密度作为节点角坐标的函数;第三行:i(节点度排名),u(θ)激活物密度;
涌现,是指复杂系统在宏观所展现出来的,无法归约到微观的特性或规律。新兴的因果涌现理论有望为量化多尺度复杂系统中的涌现现象提供强大工具。由北京师范大学教授、集智俱乐部创始人张江等人发起的「因果涌现」系列读书会第三季,将组织对本话题感兴趣的朋友,深入探讨因果涌现的核心理论,详细梳理领域发展脉络,并发掘因果涌现在生物网络和脑网络、涌现探测等方面的应用。读书会自7月11日开始,每周二晚19:00-21:00,预计持续时间8~10周。欢迎感兴趣的朋友报名参与。

详情请见:
因果涌现读书会第三季启动:深入多尺度复杂系统核心,探索因果涌现理论应用
推荐阅读