2021年诺贝尔物理学奖表彰“为我们理解复杂物理系统所做出的开创性贡献”,认可复杂系统在自然科学中的基础作用。为了庆祝这一里程碑式的成就,JPhys Complexity 编辑委员会包括 Ginestra Bianconi、吕琳媛在内的18位相关领域学者表达了对几个选定主题的思考和观点,包括:如何定义复杂系统?复杂科学在未来二十年最大的挑战是什么?2021年诺贝尔奖对复杂系统研究意味着什么?复杂系统跨学科研究的优势和挑战是什么?希望这些公开讨论对今后复杂科学的研究有所启发。
关键词:复杂系统科学,统计物理,复杂网络,气候变化,随机性,涌现,跨学科研究
Ginestra Bianconi等 | 作者
朱欣怡 | 译者
刘哲依、梁金 | 审校

原文题目:
Complex systems in the spotlight: next steps after the 2021 Nobel Prize in Physics
原文链接:
https://iopscience.iop.org/article/10.1088/2632-072X/ac7f75
2021年诺贝尔物理学奖认可了复杂系统在自然科学中的基础性作用。为了庆祝这一里程碑式的成就,这篇社论汇聚了JPhys Complexity 编辑委员会对该领域的成就、挑战和未来前景的观点。为了区分每位编辑的意见,全文由编辑对几个选定主题的一系列观点和思考组成。本文呈现了对复杂科学领域的全方位、多角度的观点。我们期冀并相信,这次公开讨论将对今后复杂系统的研究有所启发。
2021年诺贝尔物理学奖终于垂青复杂系统研究领域。奖项一半授予真锅淑郎(Syukuro Manabe)和克劳斯·哈塞尔曼(Klaus Hasselmann),另一半授予乔治·帕里西(Giorgio Parisi),以表彰他们“为我们理解复杂物理系统所做出的开创性贡献”(for groundbreaking contributions to our understanding of complex physical systems)。作为 JPhys Complexity 杂志的编辑,我们祝贺诺贝尔奖获得者取得的非凡成就,这些成就深刻地改变了我们看待地球系统和复杂系统的方式。如2021年诺贝尔奖的新闻稿所言 [1]:“他们奠定了研究地球气候以及人类如何影响气候的基础,同时彻底改变了无序物质和随机过程的理论。”
为纪念2021年诺贝尔物理学奖,JPhys Complexity 的编辑们写下这篇社论,旨在回顾复杂系统研究迄今取得的进展,辨明该领域的关键科学挑战、环境挑战和社会挑战,并概述未来二十年复杂性研究的前景。为了保持个人观点的独创性,我们将这篇社论组织成一系列稿件的形式,每位编辑都将从具体问题出发,回答如下问题:
1.定义复杂系统。复杂系统的定义在过去一直备受争议:你如何定义复杂系统?
2.未来二十年最大的挑战。复杂科学在未来二十年最大的挑战是什么?
3.2021年诺贝尔奖的含义。2021年诺贝尔奖对复杂系统研究意味着什么?
4.复杂系统的鲁棒性与脆弱性。复杂系统通常被认为是鲁棒的。然而,从气候变化到理解疾病的起源,复杂科学面临的最紧迫的挑战都涉及到:如何响应严重影响复杂系统功能的扰动?2021年诺贝尔奖授予识别复杂系统中微扰和涨落作用的研究。你能评论一下复杂系统的鲁棒性和脆弱性之间的相互作用吗?你能找到突出这种相互作用的关键科学问题吗?
5.复杂性的预测。复杂科学仍然是最难做预测的学科之一。为什么会这样?我们能从成功案例中学到什么?
6.交叉学科的优势与挑战。复杂科学是一个交叉学科。复杂系统跨学科研究的优势和挑战是什么?
7.最后评论。为庆祝2021年复杂系统研究荣获诺贝尔奖,你还有什么想说的吗?
每位编辑都独立地作出了贡献,且没有阅读其他编辑的观点,故我们能看到不同视角下的复杂系统。因此,在整体上,本文全面地总结了该领域的关键性挑战。即使对于那些在答案上有广泛共识的问题,这篇文章也成功地证明了它们的共识程度,至少在 JPhys Complexity 的编辑中是这样。例如,在这篇文章中,我们对复杂系统的定义达成了一个重要共识,即:复杂系统是由许多元素组成的表现出涌现现象的系统。这无论如何不应是理所当然的,因为在历史上,复杂系统的定义一直在文献中有着广泛的辩论(批评性的讨论见Janos Kertesz的贡献)。在其他重要领域也有广泛的共识,包括网络在编码复杂系统底层结构中的基本作用。从动力学的角度来看,这篇社论也强调了随机性(stochasticity & randomness)和非线性的普遍存在。总的来说,这些方面意味着任何对复杂系统动力学状态的预测,都必然具有概率性质。
我们想,这篇社论是一部不同乐章和谐共谱的交响乐。在这部交响乐中,“整体大于部分之和”。特别是,这篇社论包含了已被广泛接受的概念和思想,展示了一个非常坚实的共同基础。与此同时,许多观察仍然是独立的,高度个人化和原创性的,反映了JPhys Complexity 编辑们不同的研究焦点。
该社论可以一次读完,或者间断地,依据读者对每个编者、对所选问题列表激发的好奇心浏览目录中的各个编者,来缓慢地检索和阅读。
我们希望这篇社论的读者能欣赏本文所附稿件中提出和讨论的不同见解;希望这篇社论能提供关于复杂系统研究的一般观点,这将成为该领域未来工作的灵感源泉。
社论的结构如下:主编 Ginestra Bianconi 的开场白,接着是各编辑的观点,按姓名字母排列。
Ginestra Bianconi,英国玛丽女王大学,艾伦·图灵研究所
虽然历史上复杂系统的定义一直备受争议,但我相信,目前复杂系统的具体定义有一个广泛的共识:复杂系统是由相互作用的元素组成的系统,且整体上有涌现现象。然而,这一定义仍有一些不明确的条件。例如:多少元素才足以显示复杂的涌现现象?有趣的是,这个数字可以很大,如人脑中的神经元和突触的数量,但也可以相对较小,因为我们知道秀丽隐杆线虫(Caenorhabditis elegans)的大脑只由几百个神经元组成,但它却可以表现出非常重要的行为。最小的细胞也仅由几百个基因组成,并且能够存活。从这些例子中可以看出,真正的复杂性和涌现现象所需要的元素数量可能远远不是物理学中通常考虑的大数(阿伏伽德罗常数:一摩尔气体中的分子数,约为6×1016)。
通俗来说,复杂性从随机性和有序性的“较量”中产生,复杂系统的基本拓扑结构与其元素之间相互作用网络(网络方法[2])中一定程度的随机性,或其相互作用的符号(自旋玻璃方法[3])内在相关。
尽管复杂科学在过去50年里取得了惊人的进展,但我认为我们还远没能完全理解复杂性,因为我们还不清楚:一个系统产生涌现的必要条件。例如,我们离完全理解大脑功能还很远。因此,与其他更传统的科学(例如物理学)相比,这个领域可能看起来支离破碎。但我更倾向于把这看作复杂系统的优势,因为其内容丰富。我坚信:要解决复杂性问题,就真的需要探索复杂系统的各个方面,需要开放的想法描述和预测复杂系统的数据,避免预设的自上向下的教条。
>> Ginestra Bianconi 教授曾受邀参与集智「高阶网络」读书会,介绍高阶网络与动力学,欢迎加入读书会观看回放视频:
复杂科学面临着一些迫切的挑战,关于复杂系统对社会的影响和对人类的紧迫性。诺贝尔奖早就应该授予真锅淑郎(Syukuro Manabe)、克劳斯·哈塞尔曼(Klaus Hasselmann)和乔治·帕里西(Giorgio Parisi),以表彰他们对复杂系统的研究,我希望这一诺贝尔奖将有助于社会更广泛地认识到解决气候变化这一紧迫问题的必要性。
显然,气候变化研究(其先驱已获得2021年诺贝尔奖)是当务之急,其重要性和紧迫性怎么强调都不为过[4, 5]。这一领域正在迅速扩大,需要结合跨学科办法,以应对气温升高后对气候、环境和生态系统的挑战。从社会科学的角度来看,气候变化也很重要。因为了解人类社会如何应对气候变化,并提出改善全球合作的方法,这对地球的未来极其重要。
复杂科学也是理解和预测大规模流行病演变以及向政策决策者和公众通报流行病传播风险的关键。事实上,网络科学界早在新冠肺炎之前就意识到:利用无标度(scale-free)全球运输系统易导致传染病全球化的危险[6]。但不幸的是,新冠的流行仍让大多数国家感到意外,因为大多数国家的应急计划没有真正为新冠肺炎这样规模的流行病做好准备。尽管病毒的生物演变存在许多不确定性,为了监测流行病的演变和任何未来情况,科学家们很可能将大量关于社会流动性的数据与模型预测结合起来,这些模型是监测流行病和向决策者提供信息的关键依据。
在未来二十年里,复杂性和生物学交叉的进展将是精准医疗取得迫切进展的关键。这一巨大的复杂性挑战将需要一种真正的跨学科方法,结合网络科学、机器学习和人工智能与分子生物学和神经科学。事实上,虽然在过去几十年中,生物学一直广泛地使用单分子方法或严重依赖于分子生物学的中心法则,但现在人们已经充分认识到,大多数疾病是复杂的,为了理解这些疾病,重要的是要理解细胞相互作用网络的复杂性和异质性。在神经科学中,脑科学的研究正在蓬勃发展,然而系统的复杂性具有固有的多尺度特性,并且在分子水平上由于相互作用的丰富组合,这就为全面理解大脑功能带来了挑战。
最后,在未来二十年,复杂性将成为奠基量子互联网的关键,这需要将量子信息的进展与我们对经典复杂通信系统(如当前的互联网)的理解结合起来。
2021年诺贝尔奖让人们意识到气候变化的重要性,也是对复杂系统研究权威性的声明。历史上,随机动力学一直是物理学中的边缘学科,甚至具有概率性质的量子力学也是由确定性动力方程(薛定谔方程是确定性的)决定的。然而,随机性是研究复杂系统的基础,从气候学到自旋玻璃,再到复杂网络,而且,随着学科范围的扩大,随机性甚至成为生物学、社会科学甚至工程学的基础。2021年诺贝尔奖认可,由随机性驱动的复杂系统动力学是值得获得最高科学奖的主流学科[3–5, 7, 8]。这对整个复杂系统社区来说意义重大,并将推动该领域的研究,希望也能推动该领域的资金支持。2021年诺贝尔奖是社会发展的一大步,也是对(一直受到虚假信息挑战的)气候变化科学研究的进一步认可。
复杂系统研究拥抱复杂系统的天然随机属性,如今已获得2021年诺贝尔奖的充分认可。然而,我们仍有必要进一步理解复杂系统的鲁棒性和脆弱性之间的关系。例如,一个紧迫的问题是:我们离气候临界点还有多远?
网络鲁棒性的另一个重要应用在脑科学研究,大脑无疑是一个鲁棒的复杂系统,然而了解疾病如何影响大脑功能非常重要。为了解决这个问题,我认为我们需要接受大脑活动的随机性,并进一步了解大脑功能和大脑网络拓扑结构之间的相互作用。
多亏了网络科学的基础性成就,我们已经知道:网络对随机损伤的鲁棒性在很大程度上取决于网络的统计学性质。实际上,网络的无标度分布极大地改变了渗流的相图,表现出与规则格点或随机图上的渗流截然不同的临界行为[9–12]。这些结果对于理解复杂系统的底层网络结构及其动力学之间的相互作用至关重要。在我看来,应用拓扑学和随机几何学工具,可能会使我们在理解网络和更高层次网络的拓扑结构和动力学之间的相互作用方面取得更大的进展。在一定程度上,这已经实现了[13, 14]。我认为,采用拓扑和几何论证来理解复杂网络和高阶网络的动力学,对于揭示大脑研究和复杂系统中的一些未解之谜,可能是一个转折点。
>> 探索大脑复杂系统,关注「神经动力学」读书会:
详情请见:500+神经动力学社区成员,邀你共同点亮更多脑科学研究的岛屿
复杂系统的预测具有挑战性,当然也受到普遍存在的非线性动力学的限制。然而,在过去二十年里,有关复杂系统预测的工作已经取得了重大进展(例如,在预测流行病传播方面取得了前所未有的进展)。复杂系统预测能力的提高主要得益于建模者能获得大量数据,以及复杂科学与数据科学、人工智能(AI)相结合所能取得的重要进展。有趣的是,在复杂科学中,预测能力的提高往往需要使用黑箱工具,黑箱工具在人工智能中发挥着重要作用,同时带来了内在风险。我坚信,结合网络科学、数据科学和人工智能算法,增强对复杂系统的预测能力,对于包括意义非凡的气候变化研究的各种应用来说至关重要。
然而,从结果的可解释性出发,简单模型理解复杂系统的能力最为重要:简单模型可能无法捕捉复杂系统的所有细节,但它是我们理解和驯服复杂性的希望,我相信它们对更好地设计人工智能算法也至关重要。自旋玻璃理论(Spin-glass theory)告诉我们,一个实际上非常简单的模型(在一个全连通的网络上,仅仅向伊辛模型添加一个正负相互作用的随机混合)可能就已经非常复杂了[3]。类似地,只考虑具有幂律度分布的无标度网络,就可以极大地改变网络的动力学特性,从而影响临界现象的相图[12]。这些简单模型有很多好处,因为它使我们能够识别复杂系统关键属性引起的关键影响,例如复杂系统中每个元素相互作用符号的异质性或相互作用数量的异质性。
跨学科研究的优势在于该领域具有包容性,并因不同学科的科学家提供的不同视角而得到丰富。这使得我们能够从自下而上(bottom-up)的角度来处理与复杂系统的普遍共同属性相关的问题,这种视角是自上而下(top-down)方法(在上个世纪一直主导着复杂性研究)的基础和补充。此外,由于有来自不同学科的新研究问题、新数学工具、新实验结果,而且还能避免自我参照的陷阱,所以跨学科研究发展迅猛。
跨学科研究的一个重要挑战是:形成一种多学科都接受的共同语言。网络科学和机器学习面临着这一挑战,但它们在很大程度上已成为了不同学科都接受的框架。然而,在撰写跨学科论文时,发展共同语言也意味着共享优先事项并在科学关注焦点上达成一致,在这方面仍然存在许多差异。此外,不同学科的研究风格也各不相同(如撰写文章的时间、作者列表顺序的惯例、期刊出版物与会议出版物等)。因此,跨学科的合作可能需要相关科学家对彼此工作方式先行适应。
我衷心祝贺2021年诺贝尔奖获得者取得的非凡成就,以及将基础研究领域拓展到复杂系统!我也要向致力于复杂系统和从不同角度应对这一领域的许多挑战的整个复杂性研究社群表示祝贺。最后,特别感谢为这篇社论做出贡献的 JPhys Complexity 的编辑们。我希望这篇社论中出现的关于复杂性的集体观点将成为该领域未来发展的参考点。
Alex Arenas,西班牙罗维拉-威尔吉利大学(Universitat Rovira i Virgili)
据我理解,复杂系统是一组分散的又具有许多内在联系(通常是网络化的)的实体,其中每个实体与其邻近实体在局部自主运行(self-operate),并表现出全局的涌现行为。这个简单而抽象的复杂系统定义与不同学科中被认为“复杂”(complex)的各种系统是一致的。
复杂科学的主要挑战是发展一个闭环的理论来支配复杂系统的涌现行为。我认为这样的理论框架可以通过融合张量代数(tensorial algebra)、统计和非线性物理学以及光谱理论(spectral theory)而达到。
2021年诺贝尔奖代表了复杂系统领域的最高成就,使其被公认为下个世纪的基础物理学。
我认为,复杂系统中的鲁棒性和脆弱性必须从传播(propagation)的角度来理解。系统对扰动的鲁棒性越强,系统的其他性质从局部传播到全局就越困难,而脆弱性则相反。系统对扰动越脆弱,系统中任何其他性质从局部传播到全局就越容易。这里的困难和容易,指的是与传播过程相关的时间尺度。从微扰理论(perturbation theory)的角度理解鲁棒性和脆弱性,是复杂系统分析发展的一个关键方面。
总的来说,我认为预测的挑战来自于非线性,这种非线性与对称性破缺中的相互作用有关。尽管如此,预测可以用近似来实现,在物理学领域的其他领域也是如此。本领域在现实世界中强有力的证据是:对流行病演变的预测。
作为一个跨学科的领域,复杂科学的优势在于可以用复杂系统的观点来处理大量的科学问题。正如其他跨学科领域一样,面临的挑战是构建共同的科学语言、共享的科研方法。
我祝贺复杂系统学界经过多年努力,终于在物理学界占有一席之地。
Jacob Biamonte,北京雁栖湖应用数学研究院
根据我的经验,许多现代科学家都持有一种隐含的还原论中心(reductionism-centric)观点。我从两个方面看到了这个问题。第一种是理论家认为,任何描述都可以归结为自然的基本定律;第二种是理论家梦想着通过越来越小的构件来精确描述世界。
先看第一种观点。例如,开普勒的行星运动定律和伽利略的地球运动理论都可以归结为牛顿力学。前者的所有解释都包含在后者之中:这让还原论者很高兴。
第二种甚至可以描述现代工程学的方法。想象一辆新的 Corvette 跑车,一辆漂亮的车。一个独立的工程师团队负责组成这台机器的每个部件的精确工作。为了理解汽车的工作原理,我们只需把它分解成我们能理解的小零件。这似乎再次增加了还原论的可信度。
这两种方法的问题是无论还原论多么完美,它都可能失败。也许你能争辩说,一个给定的理论应该总是与一些更基本的东西有关。然而,这个基本理论的效用又值得怀疑,因为这常常导致不切实际的理论。当面临着用“更基本的描述”做出预测时,问题就出现了。如果这样做需要宇宙年龄的时间(或更长时间)才能完成的计算呢?例如,当相互作用系统的组分导致一个系统在理论上可以有比可见宇宙中电子数量更多的物理态时。不难找到这样的系统,你面前的计算机就是其中之一,谷歌和IBM正在建造的现代量子处理器是另一个代表。这种系统的集体行为变得极其难以预测,许多预测都是基于对构件的从头计算描述的巨大偏离。
我怀疑关于定义的争论源于:有许多不同的复杂系统。几十年来,顶尖网络科学家们有一个有趣的发现,那就是如此多的复杂系统共享相关的属性。这些性质可以反映在用来模拟复杂系统相互作用的图中。另一个有趣的复杂性研究方法来自计算机科学。计算机科学家把问题分成几类,并试图确定解决一类问题所需资源(计算步骤)的下限。许多正在研究的复杂系统可以很容易地模拟通用计算。
你可能会说我有偏见,但我们仍然缺少一个复杂网络的量子理论。这并不是说没有取得有趣的结果。例如,Bianconi–Barabási 理论(Bianconi–Barabási theory)在2001年就已经将网络标度律(network scaling laws)与玻色-爱因斯坦凝聚(Bose–Einstein condensation)联系起来[15],许多后续的论文都基于这些发现。量子信息理论逐渐对物理学甚至技术产生广泛影响。2010年,Perseguers,Lewenstein,Acín 和 Cirac 发现随机网络中的量子效应会产生意想不到的连接子图[16]。这些结果引起了人们的兴趣——例如:可参见我与 Facin 和 De Domenico [17]共同撰写的综述。尽管量子理论中出现了大量的网络,但网络性质和量子效应之间的关系还没有完全弄清楚。
根据 Philip Anderson(1977年诺贝尔奖获得者)的说法,“自旋玻璃的历史完美地应证了一句格言:‘一个真正的科学奥秘值得为其本身而探索到底,而不受任何明显的实际重要性或智识魅力的影响。’”我认为诺贝尔奖让更多的人关注到了奇妙的自旋玻璃世界。我们可能不愿意谈论的一个方面是:许多复杂性研究是由世界各地应用数学和计算部门的物理学家完成的。也许2021年的诺贝尔奖将扩大此类话题在物理学界中的作用?
许多结果表明复杂系统可以很容易地用通用计算机模拟仿真。不过,许多研究人员认为相变点极难建模计算。我认为成功源于不试图解决看起来不可能解决的问题。实际上,预测特定的系统性质可能很困难,但其他性质,在一般情况下,却可以在不完全了解(或计算)系统的情况下确定。
我进入这个领域是为了研究复杂网络的量子理论。这个话题很有趣,因为量子效应并不总是与明显的网络特性相关,而传统复杂系统的许多特性却与之相关。我想这样做的好处是可以研究有趣的新课题,缺点可能是研究并不总是明确地落入某一特定的主题。
我想,复本对称性破缺(Replica symmetry breaking)是一个美丽而永恒的理论。自旋玻璃奇妙永恒的语言,已经从各方面逼近了玻璃理论。但我认为,Giorgio Parisi 的工作将使人们更加关注与玻璃有关的最古老、最成功的理论。这一点尤其重要,因为新一代人将从完全不同的角度处理这些问题的变体。这些研究人员中,有些人的背景更多地是量子理论和凝聚态(实际上与传统的统计力学相差甚远),而另一些人的背景则完全是计算机科学和神经网络。复杂系统通过自旋玻璃的语言进入其他领域,已经不是第一次了。如果历史有什么可以借鉴的,那就是这不会是最后一次,仍然有很多需要学习。
Lincoln Carr, 美国科罗拉多矿业学院(Colorado School of Mines)
Thurner、Hanel 和 Klimek(THK)最近出版了一本优秀的书《复杂系统理论入门》(Introduction to the Theory of Complex Systems)[18],他们在书中假设复杂系统是相互作用元素共演化的多层网络。他们从复杂性角度认为,相互作用可以用一个三指标张量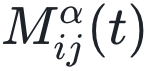 来描述,元素状态可以用含时函数
来描述,元素状态可以用含时函数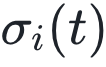 来表示。虽然我不确定这是否涵盖了可观测的物理复杂性的所有方面,但它确实导致我们在自然界许多不同系统中看到的大量惊人的普遍数学特征。与纯粹经验主义(pure empiricism)、确认偏差(confirmation bias)或人类模式识别倾向的假设相反,这些普遍存在的数学共性经过在该领域一段时间的研究后变得无可辩驳,我们称之为“复杂系统”。
来表示。虽然我不确定这是否涵盖了可观测的物理复杂性的所有方面,但它确实导致我们在自然界许多不同系统中看到的大量惊人的普遍数学特征。与纯粹经验主义(pure empiricism)、确认偏差(confirmation bias)或人类模式识别倾向的假设相反,这些普遍存在的数学共性经过在该领域一段时间的研究后变得无可辩驳,我们称之为“复杂系统”。
将复杂科学从一组不同物理系统之间的经验可识别的数学共性,转变为物理复杂性类别(physical complexity classes),可能是个世纪问题。然而,考虑到计算复杂性分类(computational complexity classes)的巨大进步(与我们在这里讨论的物理复杂性不同)以及物理复杂性概念和数学标识符的应用范围不断扩大,我相信我们有望在未来20年取得重大进展。我认为物理复杂性包括:
(1)非平凡非马尔可夫环境;
(2)多尺度层次结构;
(3)持久的动力学宏观态;
(4)非高斯或“厚尾”统计;
(5)分数几何;
(6)巨大并且仍然高度结构化的概率空间;
(7)多重约束和权衡的存在;
(8)多样性;
(9)选择原则;
无论这十多个方向复杂性的起源是否如Thurner、Hanel和Klimek[18]认为的那样是一个单一数学概念,我们仍旧缺乏来自基础物理学的一组物理假设来产生这样的概念。对我来说,这就是复杂性的终极问题:复杂性何以存在?
对我来说,2021年诺贝尔奖最重要的成果是:强调了复杂科学对于理解和解决世界上最紧迫的生态和环境问题的必要性。我们将如何解决人类面临的世界末日问题?仅仅理解引力和量子力学、能量和熵,甚至是如何设计一个鲁棒的电路,都是不够的。控制论、地球工程学和生态学正逐步向正确的方向前进。但最终解决全球气候变化问题需要系统方法,需要对许多领域的复杂性有深刻了解。2021年诺贝尔奖是跨学科的,从气候建模和二氧化碳与气候变暖的联系,到无序的复杂材料,很精彩!2021年诺贝尔奖给我们的第二个启发是:进一步发展需要跨学科协作,仅仅物理学是不够的。
在 Carlson 和 Doyle 的综述[19]中,鲁棒性和脆弱性之间的权衡写得相当漂亮!这篇文章将来自控制、通信和计算的一组概念——高容错性(highly optimized tolerance,HOT)作为复杂性的基础预测理论,将生物学、工程学等领域的实例(如细胞和CPU)联系在一起。高容错性在很大程度上依赖于鲁棒性和脆弱性之间的相互作用,而且成为一套比物理学家最偏爱的自组织临界性更有效的解释和预测原则。
最近,复杂科学中一个不断壮大的分支一直致力于理解纠缠量子系统中的复杂性[20],特别是在噪声中等尺度量子(intermediate scale quantum,NISQ)计算机的背景下。量子环境为理解和预测复杂性增添了困难,比如量子电路中预先编程的复杂性与量子态中的涌现复杂性之间的相互作用[21, 22]。然而,量子与经典复杂性的一个强有力的共同特征,就是鲁棒性和脆弱性。
元胞自动机是复杂科学中的一个历史性课题。它最初被认为是一个潜在的物理学统一理论,事实上更善于产生复杂性。具有局部相互作用的简单元素的集合产生一系列涌现行为。例如,基本元胞自动机(elementary cellular automata )就像人们想象的那样简单:一维、最近邻,并且基于经典比特。然而,它们却能产生随机性、分形,甚至图灵完备计算(Turing complete computation)。量子元胞自动机将经典比特的概念推广到量子比特(qubits),并将局部比特更新规则推广到条件酉算子(conditional unitary operators);但是,概念基本上是相同的。这正是可逆量子元胞自动机中的权衡或金发姑娘原则(Goldilocks rule)[23],它在量子系统中的鲁棒性和脆弱性之间权衡。纠缠的量子态本质上是脆弱的,在退相干前只能承受有限的量子操作。这意味着 NISQ 计算通常受电路容量(circuit volume)限制,粗略来说:电路容量 = 总的电路深度(circuit depth)*量子比特数量。Goldilocks 量子元胞自动机创造了一种新层次的稳健性。它们为任意数量的量子比特创造复杂性,并且仅受电路深度的限制[24]。这还不是量子纠错,而是复杂系统固有的鲁棒性-脆弱性权衡的应用,在 NISQ 计算机上产生了相当非凡的结果。
复杂科学是一个非常年轻的领域。我认为,目前预测的局限主要源于缺乏基本原则。先考虑一个正面例子:量子力学。从牛顿开始的光谱学中大量的实证数据引发了对其数学模式的观察。这些数学模式反过来又为视角的转变创造了机会,即以经典粒子为基础到以概率波为基础。从光谱学的困惑到支持物质原子理论的实验观察,三个世纪的科学研究使人们逐渐认识到,需要一种新的视角。量子力学的分支研究仍然应用在今天量子信息科学和技术中。复杂性,就像激发量子力学的实验一样,呈现出许多令人困惑的结果,似乎与统计物理学的基本概念不相符。什么样的基础理论能预测它?为什么它如此普遍,能跨越如此多的领域,如此多的尺度,从量子计算机到大脑到行星?
复杂性理论,是否像经典物理学中的混沌理论一样,需要改变已知理论的视角,也许需要对统计物理学和信息论进行重新表述;还是像量子力学一样,需要一个全新的范式?这些都有待观察。如果我们能回答这个问题,那么我相信复杂科学将可以预测。
我有时觉得我们物理学家对复杂系统有一种特殊看法。我喜欢从其他领域的书中学习不同的视角,例如 Scott Page 的《多样性与复杂性》(Diversity and Complexity)[25]。我们每个人都来自这个领域的不同学科,都倾向于把复杂性与我们喜欢的特征联系起来,无论是复杂网络结构还是自然选择。问题是,我们如何找到一个复杂性理论,在如此跨学科的环境中真正涵盖所有人的偏好?
这样一个跨学科领域的最终挑战是:真正地学会倾听。我特别钦佩圣塔菲研究所,因为它创造了一个环境,让生物学家、经济学家、物理学家和其他许多人真正地坐下来,相互倾听和学习。
我很荣幸能在这样一个由杰出的早期思想家启发、最近还受到诺贝尔物理学奖认可的领域工作。我记得在本科时曾听过“物理学即将死亡”这一说法,就好像当时如中微子振荡之类的重要问题,将很快得到彻底解决。我认为这个诺贝尔奖显示了物理学作为一种视角仍然在扩展和发现惊奇。它不仅令人惊叹,而且对人类福祉至关重要。
我想说,当我们仅仅从系统构成元素的功能的知识出发,去预测系统对扰动的响应而遭遇局限性,复杂系统由此定义。
最紧迫的挑战是收集大数据,量化复杂系统对扰动的响应,并推断因果关系,提取有意义和可解释的结论。
显然,这个诺贝尔奖意味着,回答复杂系统的基本问题,我们需要放弃对任何确定性答案的期望。相反,我们应该承认,正确和最具洞察力的答案都是概率性的。
正如我对上一个问题的回答,我们需要改变我们的思维方式。例如,用概率的方法描述复杂系统对扰动的响应。
复杂系统的内部结构过于复杂,无法以唯一确定的方式对给定的扰动做出响应。实际上,非线性意味着初始条件的微小变化可能导致非常不同的结果。因此,预测也需要考虑与非线性相关的不确定性。所以预测模型需要包括预测情景的置信水平。天气预报可以作为我们相当熟悉的一个概率预测的例子。比如,今天的天气预报说:“明天有六成可能性会下雨”。
复杂科学家习惯于将多样的现象放进简单模型中。然而,没有受过科学训练的人往往无法理解这种方法的力量。我认为,培养公众理解复杂系统的直觉仍然任重道远。
牛顿式的确定性方法在研究复杂系统时存在局限。因此,我们需要一个新的方向——概率的方法。
Janos Kertesz,Central European University, Complexity Science Hub Vienna (奥地利),European Center for Living Technologies(意大利)
复杂性的定义尚未达成共识并非偶然[26],这植根于这个学科的本质。复杂性普遍存在,因此表述应该是非常具有一般性的,而相关系统的可变性又非常大。事实上,科学史的大部分内容都是与复杂性作斗争:科学试图发现和理解并不复杂的现象和孤立的系统,从而可以应用非复杂性的方法。这种方法的惊人成功要归功于尺度分离,这是复杂系统中通常没有的特征。
我上课时,并不尝试定义什么是复杂系统,而是列出一些总是存在的属性(许多相互作用的组分、集体性、非线性、反馈机制、涌现现象),以及一些经常存在于复杂系统中的属性(层级组织、有序性、适应性),并明确复合系统(complicated system)和复杂系统(complex system)之间的区别。
挑战将出现在基础复杂科学及其应用中。下面我将列举一些从基本问题到应用问题的例子。
许多真实的、复杂的、远离平衡的系统是独特的,即,这样的系统只有一个历史(和未来),这就是它的全部。例子包括生物进化、人类历史、经济动力学等。Stuart Kauffman 关于“相邻可能性”(adjacent possible)的开创性工作[27]是这方面的一个重要发展,还有更多值得期待的。对于这样的系统,统计物理学的基本概念“系综”几乎不适用,甚至关于“自平均”的问题也没有什么意义。所有尺度上的不稳定性和罕见事件导向非常不同的历史,其中只有一个是相关的。存在与此基本问题相关的概念性挑战。
我们付出了大量精力研究复杂系统功能和拓扑结构的关系,但离系统地理解还差得很远。近年来,网络科学的工具箱有了重大进展,研究范围囊括了多层和高阶网络[14, 28, 29],这将引发这一方向的进一步研究。同样,在不久的将来,主要的挑战将是在一些形成“物理网络”(如大脑和分子网络)的复杂系统中,识别由连接的物理性及其相关的体积排斥效应所产生的影响 [30]。
由于意识在适应性中的作用,涉及人类的复杂系统尤其具有挑战性。然而,人工智能的出现将会带来更高层次的复杂性。为实现可解释性、确保隐私和个人数据的个人控制,人工智能从集中控制到分布式实现的范式变化有着强烈而合理的趋势[31]。在这样一个人类和人工智能的复杂生态系统中,会出现意想不到的涌现现象,对它们的理解和控制可能对平稳运行至关重要。
我们的世界充满了与复杂系统有关的严重问题;战争、流行病、金融危机、气候变化、日益严重的不平等和犯罪,还只是冰山一角。我认为(也希望)复杂科学在决策中的作用不断增加——复杂科学家的理解仍然相当不完整,但在许多情况下,他们仍然是理解最多的人。这方面令人鼓舞的例子有:一些国家对新冠肺炎的处理。复杂科学面临的最大挑战之一,也是复杂科学家的责任之一,即推动这一进程,专注于理解上述和类似的问题,公开结果,并提出可能解决方案的建议和方案。
诺贝尔奖获得者的工作在许多方面塑造了我们对复杂系统的理解。真锅淑郎和克劳斯·哈塞尔曼已经证明:物理洞察与先进的数值技术相结合,可以帮助理解复杂系统,并导出像全球变暖这样的坚实结果。早该颁发给 Giorgio Parisi 的诺贝尔奖纪念他的众多贡献,包括无序系统中的尺度和多重最优的概念[32–34]。诺贝尔奖总是会推动获奖者活跃的科学领域,复杂科学也应该如此。然而,诺贝尔奖对研究的影响大多是次要的:公众的注意力,决策者的冲动,等等。意大利已经出现了后一种迹象,宣布了资助政策的一些变化。这样的举动自然会对研究产生影响。我希望其他国家也能效仿意大利,即使获奖者中没有他们的公民。或许整个欧洲也会发生变化,这将是最理想的,因为复杂性研究的合作空间很庞大。诺贝尔奖也可能对大学课程产生影响,吸引更多学生进入这个迷人的领域。
复杂系统大多是演化的结果;因此,它们必须具有某种程度的鲁棒性——否则我们就看不到它们。然而,这类系统也具有多样性:其中一些系统非常鲁棒,而另一些系统则比较脆弱。前者的一个很好的例子是无标度网络对随机故障的鲁棒性,然而在相互依赖网络中,这种系统的耦合可能导致脆弱性增强[9, 35]。
一个系统的鲁棒性可能来源于系统被锁定在亚稳态里,只有足够强度的涨落或扰动才能迫使它找到另一个运行状态。最近一个研究社会系统的例子表明:代表城镇社会资本的网络结构如何影响和锁定腐败风险,并解释了腐败风险的持续性[36]。
在低维混沌中(在上述意义上不应该被认为是复杂的),可预测性是一个困难的问题。在复杂系统中,由于在所有尺度上总是存在不均匀性、不同种类的非线性和不稳定性以及噪声和外部扰动的多样性,预测就更复杂了。
对于前文提到的独特的“单一历史”系统,可预测性是极其困难的。因为一个偶然意外事件可能根本改变系统轨迹,使得“从历史中学习”变得困难或不可能。预测的时间跨度非常有限,因为概率分布在这样的事件中会突然改变——而且概率的意义对于这样的系统来说也变得模糊不清。
尽管存在这些困难,但仍有成功案例——最好的例子是疾病传播预测,由于跨学科的努力和大数据的应用,实时模拟和短期准确预测得以实现[37]。由于新冠大流行,这些技术迅速成为辅助决策的方法。
在复杂系统研究中,学科交叉是必然的。困难很明显:找到共同语言还是次要的——找到能够协同合作的合适而思想开放的伙伴是真正的挑战。幸运的是,越来越多的研究者并不把复杂科学家看成他们领域的入侵者,而是认识到科学及其应用中的许多紧迫问题需要新的方法和跨学科合作。
Jürgen Kurths,德国波茨坦气候影响研究研究所,德国洪堡大学
最初,二三十年前,复杂系统(complex systems)被认为是复合系统(complicated systems)的某种对应物,因此经常指代低维的系统。复杂性是由于复杂的相互作用产生的。这一点现在已经得到了很好的扩展,我们主要研究高维系统,特别是由许多成分组成的系统,具有复杂的相互作用,我们称之为复杂系统。这使我们能够分析大脑、金融、气候或电网等重要的真实系统。(参见 Kurths 文章:《复杂系统中的突变特刊——理论、方法与应用》)
我们迫切需要发展理论和相应的技术,处理在时间和空间上不断演化的大型耦合非均质系统,这些系统受到各种扰动的影响,不限于高斯过程和小强度扰动。这需要真正的跨学科方法论,特别是统计物理、图论、随机过程、数理统计、机器学习、非线性动力学和非线性数据分析。这样,我们才能够处理今后20年现实世界中的挑战性问题,例如,通过纳入多种自然组成部分以及人类的影响及其所有相互作用对地球系统进行建模,研究网络空间及其与基础设施的关系、疾病传播等。
在这次诺贝尔奖中,复杂系统科学和气候学首次被认为是物理学的重要组成部分,这是这两个领域百年来的巨大成功。请注意以下结合物理学和气候学的里程碑:Svante Arrhenius 发现温室气体导致温度升高[38],Vilhelm Bjerkness 使用基本物理方程进行天气预测[39],Lewis Fry Richardson 撰写了他的开创性著作,《通过数值过程进行天气预测》(weather prediction by numerical process)[40]。
>> 了解地球生态复杂系统,关注「地球系统科学」读书会:
详情请点击:
地球系统科学读书会启动:统计物理与深度学习交叉前沿
一个非常经典且成功的概念——李雅普诺夫稳定性,已经广泛应用在复杂系统科学中。也就是说,我们能够分析小扰动的局部影响。然而,实际系统经常会受到不小的扰动。因此,许多最新的理论结果对于评估现实世界系统的鲁棒性和脆弱性并不十分有用。因此,发展更一般的概念来研究鲁棒性和脆弱性也十分具有挑战性。
复杂系统科学可以为各种系统的预测提供有效的技术,远超已有方法。其中一个方向是对临界转变或临界点的早期预测,另一个方向是对相当平稳的复杂动力学构造中期甚至长期的预测,我们知道非常长期的预测是不可能的,进一步的方向是在不断变化的条件下计算未来动力学的情景。后者的一个突出例子,是哈塞尔曼和真锅淑郎在20世纪80年代就二氧化碳增加对全球温度升高的影响进行的研究[4, 41–43]。
复杂网络科学从一开始就是跨学科的,当跨学科团队形成并真正合作时,复杂网络科学才取得了主要的成就。要解决未来的挑战,需要更强有力的跨学科办法。
我真的很高兴成为这个社群的一员,我指的是所有从事复杂系统科学的科学家。这是一个非常活跃的领域,在相当短的历史中,创造了许多惊喜;当然,我期待会有更多惊喜。我一直很喜欢这个社区的建设性和友好气氛。我们应该始终牢记,我们的研究对象是开放系统,我们应该在全世界的跨学科工作中保持开放,我们绝不应该遵循政治家和其他决策者对这种合作的限制。
复杂系统由以非线性方式相互作用的大量主体组成,这些主体之间的相互作用能涌现出主体之间简单相加不能产生的复杂现象。不同领域的复杂系统具有可建模和研究的普适规律。
例如,一架飞机由数千万个部件组成,但只要我们了解每个部件的功能,就可以了解它的飞行原理;而对于我们的大脑,即使我们明白每个神经元如何工作的,仍不知道意识、智慧是如何产生的。因此,能够(借助还原论)通过分解来理解的系统(即整体等于部分之和的系统)是复杂的,但它们不是复杂性科学所研究的对象。像大脑这样的整体功能和性质不是各组成部分线性之和的系统,才是我们真正感兴趣的复杂系统。这就像鸟群一样,一只鸟的飞行是力学问题,而一群鸟的飞行就是复杂性科学的问题了。
探索并揭示复杂系统的内在机制是复杂性科学研究的长期挑战。另外,随着数据可获取性的快速提升,处理大规模异构(含噪)数据并将其建模为动态系统,也是复杂性科学未来面临的重要挑战。具体而言,挑战包括:
• 如何超越相关关系,找到复杂系统中的因果关系,是近期复杂性科学领域研究的焦点,最近不断有新的方法提出。
• 大脑是复杂系统最典型的例子之一,如何从复杂性科学的角度理解大脑的功能也是一个重大挑战。这一研究将有助于解决(或者至少推进)脑科学领域诸多尚未解决的基本问题,如神经回路结构与其功能之间的关系,脑网络结构与疾病和认知之间的关联等。
• 如何超越成对相互作用分析复杂系统,是深入理解复杂系统的关键。与高阶相互作用相关的几个挑战包括:(a)从数据中识别、量化和重构高阶相互作用(和高阶结构);(b)在具有高阶相互作用的系统中,探索复杂动力学涌现的基本原则;(c)从高阶相互作用的角度研究复杂系统功能的演化与调控。
• 如何结合网络科学与人工智能,提出更好的理论和方法,以解决实际问题。
• 如何充分利用复杂性科学的理论和方法,将其与大规模的真实数据结合起来,以改善人类生活的各个方面,并为政策制定提供研究支撑。
这是诺贝尔物理学奖第一次明确授予复杂系统的研究,具有里程碑意义,这表示复杂系统科学的重要性和贡献得到了自然科学界最高奖项的认可。我相信2021年诺贝尔物理学奖将推动复杂性科学的蓬勃发展,其理论和方法将广泛应用于各个研究领域。2000年,斯蒂芬·霍金曾说:“我认为下一个世纪将是复杂性的世纪。”没错,他是对的!
复杂系统是有序与无序的混合体,这正是系统的复杂性所在,具体而言,复杂系统中的主体以无序的方式相互作用,而在无序的相互作用中又能涌现出复杂系统的有序性。这种有序对于扰动是鲁棒的。与此同时,复杂系统具有高度灵活性,其演变对各种条件十分敏感。系统的最佳状态可能是一种动态的平衡。从这个角度来看,我认为深入理解这种相互作用的两个关键问题是:定义这种复杂机制背后的简单规则,及预测复杂系统的未来演变。
复杂系统是高度动态和敏感的。我们无法奢求具体而准确地预测未来,最多只能期望预测事件发生的概率(类似于天气预报)。这并不是因为缺乏信息,而是因为复杂系统中即使是微小的扰动也可能被放大从而产生不可预测的结果(例如,蝴蝶效应、混沌……)。而对于具有稳定模式的事件,只要我们能够收集到足够多的历史数据,就可以预测事件发生的概率。
比如,通过分析用户在互联网上的行为特征,就可以推荐他/她可能感兴趣的内容(如短视频、新闻、书籍、产品等)。感兴趣的读者可以阅读邓肯·瓦茨( Duncan J Watts)的《Everything is Obvious》一书,书中有更多例子(该书的中文译本为《反常识》)。该书中提到,常识在处理简单问题时非常成功和有效,但在处理(复杂性科学中的)复杂问题时失败的概率很高。所以对于复杂问题,过去的成功经验实际上效果非常有限,甚至会起到负面作用(例如,黑天鹅)。
理解复杂系统需要跨学科研究。复杂性科学将来自不同学科的认识整合为全面的理解,可以使我们进一步发展具有普适性的方法。例如,我们可以利用物理学的知识来识别社会系统中的规律并用于解决实际问题。因此,主要的挑战在于,弄清楚哪门学科、何种视角有助于理解所研究的目标系统。对很多复杂系统而言,出现的问题是跨学科问题,即超出单一学科领域的问题,需要跨学科方法。目前的关键是如何加强多学科合作,从教育的角度来讲,需要进行一些教育改革,以培养复杂性科学研究中的跨学科研究人才,对于这一问题,我认为在不同学科课程中增加复杂系统相关课程和实践是有益的。
全世界复杂性科学研究者需要携手共创未来,我们应该加强联系与合作,共同推动复杂性科学的发展,促进复杂性科学在人类生存和发展等重要领域中发挥作用。
>> 吕琳媛教授领衔发起的「高阶网络」读书会:

Cristina Masoller,西班牙加泰罗尼亚理工大学
复杂系统要求有大量相互依赖的变量和/或大量相互作用的元素。换句话说,复杂系统具有高维相空间。多大?这要看情况,但要我说,一个复杂系统至少有10个元素/变量。第二个关键要求是系统是非线性的(元素、相互作用或两者都是非线性的)。第三个条件是系统的结构是异质的(换句话说,相互作用既不是完全规则,也不是完全随机的)。大型线性系统是“复合的”(complicated),而大型非线性系统是复杂的(complex)。
复杂系统的一个典型特性是:系统对扰动的响应是非平凡的,并且常常是反直觉的和不可预料的。换句话说,复杂系统的行为难以预测和控制。诸如插值法(interpolation)和外推法(extrapolation)之类的线性技术可能无法预测复杂系统的行为。还原论(引用维基百科的话:“作为一种知识和哲学立场,它认为复杂系统是其各部分的总和”)因为系统中元素及其相互作用的非线性本质而失效。
复杂系统的其他特征包括:
-
它们通常是多尺度的,在空间、时间上或两者兼而有之;
-
它们有记忆:由于相互作用和反馈回路中的延迟,复杂系统的未来状态不仅取决于其当前状态,也取决于系统的过去。
-
它们通常有非高斯统计的特征,并且可以显示出极端或罕见的涨落。在复杂系统的背景下,我们所说的极端涨落或罕见事件是什么意思呢?当然,精确定义取决于特定的系统,但一般来说,我们认为即使一个涨落可能非常大,如果它不会有长期影响(因为系统可以对一些非常大的涨落保持鲁棒性,并在不久之后返回到先前的状态),那么就不是极端涨落。相反,一个极端涨落(不一定非常大)或一个罕见事件可能会对系统后来的行为产生长期影响,甚至可能经历不可逆的转变到达一个不同状态。
-
多稳定性(Multistability)也是复杂系统的一个普遍特征,因为这些系统可以显示出突变(转变到不同状态),以及在存在漂移或时变参数时,有迟滞现象。
-
当一个复杂系统有许多时滞的相互作用和反馈回路时,它也可能在达到稳态之前有很长的一段转变期。
我认为,最大的挑战之一是我们社会中的信息传播。我们如何利用社交媒体和复杂科学来对抗虚假信息、阻止假新闻传播、促进合作?社交媒体和复杂科学已经建立了复杂网络中谣言传播的详细模型,我们需要知道这些结果如何应用在实际中。例如,如何利用社交网络(Facebook、WhatsApp、Instagram、Twitter等)促进合作,并阻止那些在我们社会中产生强烈两极分化的假新闻传播(例如英国脱欧,极右政党的增长,对少数族裔、移民的仇恨等)。
>> 用计算理解社会,关注「计算社会科学」读书会:
数据与计算前沿方法整合:计算社会科学读书会第二季启动
2021年诺贝尔物理学奖认可跨学科研究的重要性。复杂科学的另一个重要挑战是研究气候变化(让人们意识到这个问题的重要性,不仅需要各国政府,也需要我们每个人共同努力)。2021年诺贝尔奖认可,气候建模和非线性方法的研究帮助我们了解气候,并预测由于人类活动导致的二氧化碳增多怎样导致气候的危险变化。
由于存在非线性和反馈回路,复杂系统对扰动的响应通常难以预料,而且常常违反直觉。复杂系统由在系统的结构和功能中扮演不同角色的大量不同元素构成,这意味着存在一些关键元素,对于传播关键信息、同步系统、生成危险涨落等至关重要。因此,虽然复杂系统对于一般扰动可能非常鲁棒,但它对于特定元素的目标扰动可能非常脆弱,这可能产生严重故障的级联或雪崩。
预测复杂系统的行为非常具有挑战性,主要是因为复杂系统的三个特征:大尺寸规模、非线性和非均匀性。描述复杂系统的方程有大量变量和参数,因此,如果我们想用机器学习(ML)进行预测,无论是在数据要求还是在计算能力方面,训练都非常困难。人们可能希望,有了足够强的计算能力,在过去观测的“热力学极限”下,机器学习输出将接近复杂系统的真实动力学。然而,因为复杂系统通常是非平稳的(并且可能显示出非常长的瞬变和突变),即使我们有非常长的观测(所有系统变量的观测,具有高时间分辨率),仍可能无法以良好的置信度预测系统的未来状态。
为了理解和预测现实世界中的复杂系统,通常需要跨学科努力。在我看来,一个成功的事例是:使用复杂网络和非线性数据分析的工具来推进对我们对气候动力学的理解,并揭示常规(线性)技术无法检测到的微妙因果效应。我建议感兴趣的读者参阅参考文献[45, 46]。
进步需要合作,跨学科研究的主要优势在于它能产生重大的进步。例如,人们可以模拟非常细致的气候模型,也可以分析观测到的气候数据,但如果没有气候专家的直接参与,从模式和数据分析中获得的信息就无法促进我们对基本物理过程的理解。
跨学科研究的一个主要挑战是鼓励不同学科的研究人员相互交流,并理解彼此的需要和兴趣。各方要“走出舒适区”,努力相互理解,任务虽然艰巨,但会有很多收获。因为只有通过不同学科的共同努力才能取得真正的进展。一个例子是使用光子神经元(photonic neurons)的光子人工智能(AI)系统的开发:通过使用激光,我们可以开发出更快、更节能的人工智能系统,但要使用真正模拟生物神经元的“光子神经元”,我们需要理解神经动力学,还需要了解在光子系统中实现神经元编码和处理信息的非线性机制。
为了促进跨学科研究,需要跨学科的科学活动,将不同领域的专家聚集在一起(光子学会议不太可能找到神经科学家,反之亦然;例如,需要诸如几年前在尼斯举行的“Computational Neuroscience and Optical Dynamics”研讨会之类的科学活动来促进跨学科讨论)。在资助机构的支持下建立跨学科小组也是至关重要的,这些小组现在通常在界限分明的领域各自组织,如物理和数学、生物和医学、社会科学和人文科学。
跨学科研究终于得到了应有的认可。在我看来,跨学科研究是应对未来几年我们社会最重要挑战(气候变化、老龄化人口的健康和生活方式、假新闻和社会两极分化等)的唯一途径。
我理解许多研究者喜欢用复杂系统的常见特征定义它,但我倾向于基于它的基本性质来定义。因此,我认为复杂系统是这样一个系统:(i)由相互作用的组分组成,(ii)表现出不能从组成部分本身的行为推断出的动力学行为。在这样的系统中,组分之间的交互作用与组分本身在决定集体行为时一样重要。根据这个定义,复杂系统用网络建模交互作用就变得很自然。特别地,这种系统的控制,原则上可以基于调整组分或它们之间的相互作用[47]。
只有两个元素的系统也有可能表现出涌现行为,从而表现出复杂性。就像一对耦合节拍器的同步一样。同样,具有规则结构和重复部分的系统也可能表现出涌现性质(例如,金刚石与石墨),正如其凝聚态物理学中的表现。也就是说,复杂科学研究者通常对由大量相互作用的成分组成的系统感兴趣,我认为这应当成为定义的一部分。他们还常对无序和/或异质的系统感兴趣,因此系统的结构本身也是“复杂的”。交互网络可以相当平凡,并且不限于局部或在普通物理空间中自然地表示。从这个意义上说,我认为当前对复杂物理系统的研究是一种“后凝聚态”物理学。
挑战,既有科学上的,也有结构上的。科学上一项重大挑战是:从主导许多子领域的简单模型转向可以根据数据验证的现实模型。在每一个科学领域都必须对模型持谨慎态度,但在处理复杂系统时尤其如此。因为复杂系统的细节丰富,需要整体方法,而且经常采用粗粒化描述。在这方面,需要克服的障碍包括加强与实验科学的联系和确保所用数据的质量。
复杂科学由于其学科交叉性也面临着结构性挑战。当前许多关于复杂系统的研究都是在许多其他名称下进行的,从系统生物学到计算社会科学。相反地,自我认同的复杂系统研究者经常研究非常遥远的课题,他们可能不熟悉彼此的系统。随着这一领域的成熟,新的挑战是:如何在特定会议、期刊和学会划定的现有领域之外,界定其范围。
2021年诺贝尔物理学奖所表彰的两项工作,一个是基于数据的建模,另一个是成熟的统计物理领域的工作,这个奖项在上述两项挑战上取得了突破。特别是,它有助于确定物理学领域的范围,这将影响人才训练、招聘和新项目的申报。虽然这一影响在物理学领域最为直接,但获奖研究的高度跨学科表明,该奖项也可能对许多其他学科产生影响。
首先,我想简单评论这一问题的前景。许多真实系统因鲁棒性而存在,往往涉及相互作用。因此,它们往往是复杂和鲁棒的。虽然复杂性和鲁棒性的共演化很常见,但不难想象不鲁棒的复杂系统。对于大多数系统(无论系统复杂与否)来说,对扰动的响应都是一个重要问题,即使它们通常是鲁棒的。然而,当系统变得复杂时,可能的响应领域似乎更加丰富。
在扰动响应的研究中,复杂系统的网络表示尤其富有洞察力,因为这类系统中的扰动经常通过网络传播。这就引出了许多基本问题,它们构成我许多研究的基础[48, 49]。局部扰动何时会产生全局影响?一个系统的扰动何时会影响到一个耦合的相互依赖系统?看起来难以区分的扰动怎么会有截然不同的结果?如何预测极端但罕见的事件并解释不确定性?如何控制复杂系统对扰动的响应?后者是最重要的,因为许多具有科学意义的复杂系统以去中心化的方式发展和运作。
因为高维度、非线性和不确定性,预测具有挑战性。这些特征并不是复杂系统所独有的,但它们在这种情况下可能更重要,这是因为复杂系统的本质决定了它不能用纯粹的还原论方法探索,而开发可广泛应用的全系统降维方法仍在进行中[50]。
回顾成功的事例也是有益的。对于我们这些有混沌背景的人来说,天气预测的显著进步是一个突出的例子。从复杂科学的角度来看,这一进步似乎首先源于对天气系统的理解取得了巨大进步。因此,可以说,要提高我们预测其他复杂系统行为的能力,必须首先提高我们对支配这类系统的原理的理解。特别是,这可能为结合机器学习和基于知识模型的混合方法提供新机会[51]。
优势是见解、方法甚至现象可以从一个应用领域迁徙到另一个领域。因此,这些发现可能具有深远影响。就我个人而言,我也很欣赏在不同问题上探索研究成果的自由,我相信许多同事都有这种感觉。最紧迫的挑战是难以形成一个有凝聚力的研究团体。
这不是复杂科学研究第一次得到诺贝尔奖。在物理学方面,以前的例子包括统计物理的诺贝尔奖,如1977年的诺贝尔奖授予 Philip W Anderson,Nevill F Mott 和 John H Van Vleck,以表彰他们对磁性和无序系统电子结构的基本理论研究。
在化学方面,例如同年授予普利高津(Ilya Prigogine)的奖项“表彰他对非平衡热力学,特别是耗散结构理论的贡献”,以及最近在2013年授予 Martin Karplus、Michael Levitt 和 Arieh Warshel 的奖项“表彰他们对复杂化学系统多尺度模型的发展”。
诺贝尔经济学奖中也有突出的例子,包括1978年授予赫伯特·西蒙(Herbert A Simon)的奖项,“表彰他对经济组织内部决策过程的开创性研究”,以及1994年授予 John C Harsanyi、John F Nash Jr 和 Reinhard Selten的奖项,“表彰他们在非合作博弈论中对均衡的开创性分析”。
然而,这一切都不能降低2021年诺贝尔物理学奖“对我们理解复杂(物理)系统的突破性贡献”的历史意义。有大量报道都提到了这一事实:该奖项的基本原理比以往任何一个奖项都更广泛、更明确地提及复杂系统。
Matjaž Perc,University of Maribor, Alma Mater Europaea(斯洛文尼亚),Complexity Science Hub Vienna(奥地利)
复杂系统由大量相对简单的元素组成,这些元素共同表现出复杂的行为。简单构件搭建的系统涌现出人们难以想象的复杂。这也是一个关于生命的故事,从我们身体里的细胞,到蚁丘里的蚂蚁,到构成我们整个数字生活的0和1,到社会中的人类,到构成宇宙的行星和恒星。复杂系统跨越了我们存在的全部,它们可能就是生命的结构。
>> 生命是什么?生命如何起源和演化?关注「生命复杂性」读书会:
读书会详情:
生命复杂性系列读书会:从信息和物理视角探索生命的内在逻辑
复杂科学无处不在,但也无处存在,因为一旦脱离另一个科学领域的背景,它便很难存在。无论是物理学、化学、生物学、社会学还是经济学,复杂系统的例子在所有这些领域中比比皆是,但作为一个领域本身,复杂科学却非常难以定义。这当然是个挑战——如果复杂性科学的存在要取决于其他领域,那么我们如何论证其适用性、重要性、相关性以及资金需求。最大的挑战可能是真正理解复杂科学的广阔性和首要重要性,一旦我们理解了,就为这个领域的独立发展提供了基础和背景。(参见本文作者 Matjaž Perc 的文章:《计算美学百篇论文大综述:如何从复杂性科学视角进行审美》)
2021年诺贝尔物理学奖对复杂科学领域而言是一个渴盼已久的、也许也是一个迟到的认可,将在此领域的历史上熠熠生辉,成为其走向成熟和具有更广泛吸引力的重要里程碑。
当我们讨论复杂系统的鲁棒性和脆弱性时,重要的是要理解两者可以很容易地共存,而且这两个概念本身并不矛盾。复杂系统在远离相变或临界点时是稳健的,而超过相变或临界点,变化往往是突然和不可逆转的。
地球气候就是这一事实的很好例证。全新世(Holocene)是地球历史最后11700年的名称,在此期间,我们目睹了我们生活环境的惊人稳健性。这种稳健性让我们的生活得以演化,从农耕到农业,再到科学进步。但是我们想要的太多了,我们开发,我们收获,我们以惊人的速度燃烧自然资源。速度如此之快,以至于已经把气候推到了临界点附近。如果气候系统这个复杂系统不够稳健,全新世可能在一万年前就已经结束。但事实并非如此,是我们的极端行为把这个复杂系统推向了崩溃边缘。正是复杂科学使我们能够理解这一点,并向我们自己、科学家和公众良好传达。
橡皮筋的类比可能很恰当:复杂系统可能是非常结实的橡皮筋,可以用力拉它,它总是会回到原来的形状。直到拉得太用力,然后它将以最不可预测的、基本上不可逆转和不可修复的方式突然断裂。
预测任何有意义而又并不明显的事情总是一种挑战。有鉴于此,我们可以重新表述这个问题:就预测而言,非线性和复杂系统是否真的是唯一值得费心的系统?答案是肯定的,挑战本身就是一个显而易见的结果,如果预测没有挑战性,生活本身就会变得无聊和可预测。我们所拥有的任何成功故事可能都只是好运气,因为我们能够成功预测的复杂系统在远离临界点处运行。但其中的乐趣和成功在哪里呢?也许应该谢天谢地,现实本来就不可预测。
跨学科既是祝福也是诅咒。这是一个祝福,因为它具有广泛而普遍的适用性,如果掌握好复杂科学的基本原理,就可以探索许多领域。这也是一个诅咒,因为无论一个人做什么,无论他多么成功,都没有根据地,或者至少,它仍在建设中。这不可避免地仍然会在认可、资助和最终的职业前景方面带来挑战。情况正在改善,但我们几代人都因缺乏在复杂性科学领域从事稳定研究的机会而迷失了方向。
热烈祝贺和感谢 Giorgio Parisi,他的突破性发现使我们现在所做的一切成为可能。
Filippo Radicchi,美国印第安纳大学
当一个系统的行为表现为多个结构或动力尺度的叠加时,它就是复杂的。系统中的复杂行为通常从许多基本对象的相互作用中涌现。自然界中复杂系统的实例随处可见,包括社会、生物和科技系统。
我认为数据科学和复杂科学之间有紧密的联系。随着越来越多真实复杂系统的数据变得可用,复杂科学面临新的挑战。在这个快速发展的时代,我们很难预测未来20年的研究将考虑哪些具体问题。然而,我预计复杂科学的最大贡献将是在复杂的社会技术、生物和气候系统中。
诺贝尔奖授予复杂科学的发现,代表着对整个研究领域的重要认可。我希望它能进一步刺激对该领域的资助,并为未来几年的重大发现开辟新的可能性。这个奖非常及时。描述真实复杂系统的可用数据不断增加,以及新型真实复杂系统(如社交媒体)的出现,正在为复杂科学带来理论挑战,而在几年前,这些挑战甚至都没有清晰的概念。
一个系统在某些条件下可能是稳健的,但在其他条件下会变得脆弱。网络科学中一个著名的理论成果在这方面具有很强的代表性。复杂网络对随机扰动具有鲁棒性,但对有针对性的攻击表现出极大的脆弱性。
复杂系统中多尺度的叠加自然会使预测变得困难。由于复杂系统常有动力学非线性和混沌的特性,因此在预测动力学特性时可能更有挑战。然而,还是有一些案例成功地预测了复杂动力系统的行为。例如,分析复杂网络拓扑结构上的传染模型,可以相当准确地预测疾病在现实世界中的传播。此外,渗流理论应用于网络提供了对随机或目标破坏的网络鲁棒性的精确估计。
最大的挑战是各种层面可能存在潜在沟通障碍。例如,只有少数会议/期刊致力于复杂系统的跨学科研究。另一方面,许多重要的科学问题只有真正跨学科的研究团队才能解决。因此,如果克服了上述沟通障碍,那么跨学科的合作可能会带来突破性发现。
13. Ramakrishna Ramaswamy 的观点
Ramakrishna Ramaswamy,印度理工学院
任何一个从根本上缺乏还原论方法的物理系统,在某种意义上都是复杂系统。我挺喜欢 Parisi 的定义(在Virasoro多年前的一次演讲中听到过),“你对一个系统谈论得越多,它就越复杂”。当然,这可以是定量的,但是这个陈述抓住了复杂系统的主要特征,那就是要描述它们需要很多自由度、很多变量。
到目前为止,区分系统是否复杂似乎存在一套范式:复杂系统的例子和不复杂系统的例子。涌现和集体行为的概念很重要,但这些概念需要量化。对复杂性类型进行适当的分类,这一涉及学科特征的分类学问题仍然是一个重大挑战,这将是未来几年我们在复杂系统领域努力攻坚的方向之一。

详情请见:
因果涌现读书会第三季启动:深入多尺度复杂系统核心,探索因果涌现理论应用
14. Francisco A Rodrigues 的观点
Francisco A Rodrigues,巴西圣保罗大学
我认为复杂性主要与涌现现象和集体动力学有关。如果我们考虑它的传统定义,复杂系统是由相互连接的部件组成,我们可以说汽车或机器是复杂系统。然而,车辆只是一个复合系统,我们知道其中每个部分是如何工作的。与汽车不同,我们可以观察到复杂系统对故障具有高度容错性,系统会根据外部扰动重新组织其结构和动力学。而在一个复合系统,比如汽车或计算机中,就没有这些容错机制,这样的系统无法适应环境的变化。复杂系统能适应环境变化,并最大化其组件之间的信息流。此外,复杂系统呈现出涌现现象。我们大脑中的记忆或者巢穴中白蚁之间的合作都是涌现的例子。这些系统不存在中央控制,并且系统动力学是元素相互作用的产物。因此,在我看来,要定义一个系统是复杂系统,我们必须考虑这些集体动力学和涌现性质。
当今复杂系统建模的最大挑战是缺乏精确的数据。例如,我们有很多关于静态网络的数据,比如道路和互联网上路由器之间的连接,但关于时间和多层交互的数据却很少。时效网络(temporal networks)对于研究动力学过程必不可少,比如流行病传播,它依赖于人们在一天中的联系。时效网络对于研究物种之间的相互作用、社会联系和遗传网络也必不可少。另一方面,多层网络由相互连接的网络构成。这些网络是理解由几个层次组成的生物过程的基础——基因相互作用受蛋白质-蛋白质连接的影响,蛋白质-蛋白质连接由代谢反应决定,反之亦然。因此,复杂科学的一个基本挑战是如何获得关于我们世界的更准确的数据,不仅考虑空间数据,而且考虑实时数据。
诺贝尔奖颁给“对理解复杂物理系统的突破性贡献”,是对复杂科学的重大贡献。Giorgio Parisi 主要研究了自旋玻璃,即无序磁系统,并开发了用于研究复杂系统的数学工具。物理学界对复杂系统的认可,显示了复杂系统对人类进步的重要性。物理学不再只关注微观(量子世界)或宏观(天文学)世界,而且也关注我们生活的尺度,关注人类的主要问题,包括全球变暖、流行病、社会不平等和战争。所有这些应用都可以用复杂性理论来研究。2000年,斯蒂芬·霍金说:“21世纪将是复杂的世纪”,他是对的。
由于底层网络的无标度组织,复杂系统对随机扰动是鲁棒的。然而,韧性(resilience)不足以使系统保持运转,有一个信息流最优的网络结构也是至关重要的。因此,现在要研究的一个基本问题是:理解如何在网络中同时优化鲁棒性(robustness)和导航性(navigability)——或其他动力学特性,比如大脑中的同步性。此外,大多数研究都将对抗节点随机移除的韧性作为鲁棒性的衡量标准,但也应该考虑其他类型的韧性。例如,鲁棒性可以量化系统同步的效率或参与者合作的容易程度。假设在系统中加入一些扰动,比如一个具有不同本征频率的振荡器,或者一个复制对手策略的参与者。在这些情况下,这样的改变将不会显著影响鲁棒的系统。因此,还有其他方式来定义韧性,这一概念的理论表述是复杂科学中的一个挑战。
预测是复杂科学许多应用的基础。然而,这项任务具有挑战性,因为复杂系统呈现非线性动力学、反馈和元素之间的交互,使得这些系统难以使用来自统计学和当前的机器学习工具来预测。事实上,大多数推理方法都假设观测是独立的,它们的性质是静态的,随时间保持相同的概率分布。然而,复杂系统的元素以非线性的方式交互,表现出反馈并相互影响。因此,传统方法并不适用于预测系统演化,在许多应用中预测表现较差。
克服这些限制的一种方法是使用深度神经网络,因为它适合于非线性数据。然而,当使用神经网络时,我们在预测方面获益,但在可解释性方面损失,因为这些神经网络在预测过程中充当黑箱。因此,今天的挑战是使这些神经网络更易于解释,这将有助于理解复杂系统的组织和演化如何影响其动力学。
预测的另一个关键问题是所谓的“背景变化”(context changing)。例如,在预测 SARS-COV 2 病例数时,由于缺乏数据,大多数模型无法提供流行病开始的准确预测。后来,当我们有更多数据时,预测还是不准确,因为预测结果改变了系统的行为。当证实病例增加时,人们开始保护自己,许多政府采取了封锁政策,影响了传播动力学。因此,以前的数据不再适用,因为原先得到的同样的方程不再支配系统的演化。不幸的是,在大多数复杂系统中,这种由干预引起的动态行为的改变普遍存在。当我们使用一些新药治疗癌症时,这些药物可以改变疾病的演变。与此同时,当我们试图阻止虚假新闻在社交媒体上的传播时,这种屏蔽可以产生新的社会运动,促进传播。因此,在复杂系统中进行预测是一个巨大的挑战,只能用新的理论方法来解决,传统技术无法预测多数现实世界系统中的复杂动力学。
跨学科的主要优势是复杂科学可以加入不同的研究领域。复杂科学使来自不同学科的科学家能够就我们社会的基本问题进行讨论和合作。与其他非常专业化的领域不同,复杂性允许不同学科的整合,使知识能够以独特的方式发展。跨学科的研究将解决人类的主要问题,包括全球变暖和流行病、贫困和战争的出现。因此,跨学科是复杂科学的重要特征之一,它使得复杂科学成为必不可少、广受认可的科学。
2021年的诺贝尔奖认可,物理学不仅对与宇宙起源和演化有关的问题感兴趣,而且对当今时代改善人们生活感兴趣。如果我们要解决人类的主要问题,以可持续、日益健康和人道的方式规划我们的未来,在不耗尽我们星球的情况下,为每个人提供援助,那么,理解复杂系统至关重要。
15. Marta Sales-Pardo 的观点
Marta Sales-Pardo,西班牙罗维拉-维尔吉利大学(Univ Rovira i Virgili)
由许多相互作用的单元(通常以非线性方式)组成的系统,其宏观行为不能用单个组分的行为来解释。
我认为,我们在数据、数据建模以及如何将结果传达给社会和决策者方面,将面临许多挑战。最近的新冠大流行表明,不确定性对整个社会是一个很难理解的概念,我们的挑战将是在各种背景下明确这一概念。对于复杂系统科学,我们的目标将是更好地理解和(如果我们能)找到方法来驯服或减少不确定性。在这个方向上,我认为人工智能工具,如果以一种有意义的、可控的方式使用,可以非常强大。复杂系统科学家面临的一个挑战将是:利用人工智能工具(能够处理大量数据)的力量来理解物理系统。这将需要超越目前我们所知的黑箱预测工具,开发适合我们想要研究的复杂系统性质的新人工智能工具。
>> 探索 AI 和自然科学相互促进的新范式,关注「AI+Science」读书会:
作为一个在自旋玻璃领域获得博士学位的人,我认为诺贝尔奖授予 Giorgio Parisi 不仅是对他的创造力的认可,在某种程度上,也是对整个领域的认可;如果学界没有对 Parisi 思想的认可和进一步发展,其影响就不会如此之大。诺贝尔奖认为,复杂系统科学需要超越传统物理学领域的原创思想、数学工具和计算方法。如果没有 Parisi 和他的追随者的贡献,就没有我们现在对一些计算、生物和复杂网络问题的理解。
总的来说,我认为复杂系统通常对系统性扰动具有韧性和鲁棒性,但我们知道,有时“小”事件可能会对整个系统产生坏影响。以大脑为例,我们知道这是一个复杂系统,即使在恶劣条件下也能保持其基本功能。然而,面对某些全系统和局部的扰动,大脑也是脆弱的:例如,神经递质浓度的系统性失衡常常导致行为或态度障碍,甚至精神疾病;其它局部扰动(例如动脉瘤)可导致对脑功能的不可逆损害。以生态系统为例,我们知道,尽管它们具有惊人的适应能力和抵御不利条件的能力,但入侵物种的到来、气候变化引起的栖息地变化以及人类活动通常都会严重改变生态系统的平衡。
一般来说,复杂系统往往与许多外部因素有关。幸运的是,复杂系统通常具有自适应性和鲁棒性,能够应对这些外部因素的“小”变化,但对大的波动和其他扰动则很脆弱。
长期预测是复杂系统科学中的一个问题。我认为我们预测能力差的原因有很多:噪声、数据点的数量和缺乏良好的模型。大多数时候,我们不会为数据寻找生成模型(generative model),也就是说,我们使用启发式方法,而不是使用在给定一些假设的情况下严格量化不确定性的原理性方法。这样做的时候,噪声或数据的稀缺(或两者兼而有之)使我们很难做出预测。事实上,我们知道,我们从含噪声数据中恢复模型的能力存在基本限制[52, 53]。因为我们通常不能降低噪声水平,最好的选择是增加观测数量,以便能够为我们的数据获得预测模型。事实上,从数据中获取数学模型的工具的发展表明,通常有许多数学模型与观测数据兼容,我们的职责是在最重要的地方增加观测[52]。
对我来说,最大的挑战之一就是沟通。其他领域的研究人员有不同的语言,有时缺乏硬科学领域的科学家所接受的技术和定量训练。因此,我们需要投入大量时间,才能真正跨越学科界限,建立协同效应。一些科学家认为这是一个无法逾越的障碍,因为这阻碍他们的生产力。尽管在沟通方面存在挑战,在我看来,跨学科研究的优势让时间投入物有所值:不同领域的科学家对具体研究问题有不同看法,这些看法往往与你的看法相辅相成,丰富你的批判性思维。通过从不同角度考虑同一问题,跨学科团队不仅有可能显著推进科学,而且有可能使这些进展在科学的不同领域得到了解和承认。
我们真的应该利用这个机会向社会展示复杂科学研究在实践层面上的重要性。我认为复杂系统科学家对 COVID-19 大流行的贡献已经展示了复杂系统科学可以为与社会息息相关的问题提供答案。
我还认为,很长一段时间以来,复杂系统科学一直被视为物理学中的一门“次要”学科。2021年诺贝尔奖为复杂系统科学提供了一个机会:在物理学这一“大”学科旁边获得期待已久、当之无愧的地位。
Maxi San Miguel, IFISC (CSIC-UIB)(Institute for Cross-Disciplinary Physics and Complex Systems,跨学科物理与复杂系统研究所)
复杂性来自拉丁语“plexus”,表示组成部分的不可分离性。因此,一个好的标准定义是,复杂系统是由许多相互作用的单元组成,能够涌现出新特性,这些特性不能用单个孤立成分的特性来理解。当我们说一个系统具有涌现性质时,意思是,关于系统的有效理论在一定尺度或组织层次上与较低层次存在质的不同。
引用诺贝尔奖获得者菲利普·安德森(Phil W Anderson)的话[54],一个还原论假说绝不意味着一个建构主义假说:因此,人们可以说,作为科学范式的一次变革,复杂系统科学是涌现论(emergence)对还原论(reductionism)的胜利。复杂系统行为的两个重要特征是,它常常与多尺度问题相关联,以及长期定量预测存在固有的局限性。(参看安德森经典论文:《多者异也:破缺的对称性与科学层级结构的本质 | 经典回顾》)
我将从三个不同的方面出发:
-
在基础科学层面上,在发展处理多尺度问题的一般方法和确定涌现行为的相关变量方面,仍有许多工作要做:对于全局系统行为来说,哪些细节是重要的?此外,使用和理解人工智能技术来建立复杂系统行为中的因果关系也是一个挑战。
-
复杂科学可能产生重要影响的特定挑战领域,我认为是:(i)健康科学,(ii)与人类-技术(包括机器人)交互相关的集体现象。更一般地说,复杂性工程,即为特定目标设计复杂系统,例如非常规计算,是一个具有挑战性的机会窗口。
-
至于社会方面,最大的挑战是在沟通和教育:(i)使整个社会认识到,复杂系统方法带来了一场科学复兴,基于一种不同的思维方式,能够通过改变思维方式来改变社会。(ii)构建一个新的教育体系,让各个年龄段的学生都能学习认识现实的新方法:跨学科学习,从数据中学习。
这是对一个成熟的研究领域的认可,既有基础性的贡献(自旋玻璃),也有与社会高度相关的产出(气候模型)。气候是“地球”复杂系统中的一种涌现现象,是关于多尺度上相互作用系统的例子:从局部变量到海洋-大气耦合,再到行星级别的相关性。诺贝尔奖两部分的主要联系是对预测这一概念的贡献。引用 Giorgio Parisi [55]的话,在复杂系统研究中,预测这一概念具有较弱但更广泛的意义,因此物理学的目标领域要广泛得多,物理学构造(概念、模型、工具…..)具有远远更多的应用。气候预测现在本质上是概率性的,并基于不同模型的实现(气候系统的“复本”)。这次诺贝尔奖也是对复杂系统研究核心的跨学科方法的认可,这一点通过将自旋玻璃理论中的概念迁移到各种不同问题而得到强调。
理解、预测和控制是不同的东西。以太阳系为例,我们对它有很好的认识,但我们不能控制它。另一方面,基于数据的托勒密太阳系在预测方面很好,但在科学认识方面较差。正如我在回答前面的问题时所讨论的,预测这一概念在复杂系统中是不同的,主要是概率性的,或者与不同情景的预测有关。我们已经知道,预测是有限的:我们无法给出2031年7月4日时代广场温度的良好定量预测。另一个经验是,我们必须确定哪些问题是可以回答的。在处理复杂系统时,我们需要更好地理解可预测性的限度(或可预测性的含义)。
跨学科,不同于多学科,是复杂系统科学的荣耀与苦恼。荣耀在于不同学科之间概念和方法的迁移,这是新知识的巨大来源。苦恼在于,当一般复杂系统方法应用于一个特定的研究课题时,如果成功,它将成为一门新的独立学科,例如:城市科学。
>> 理解城市复杂系统的运行规律,欢迎关注「城市科学」读书会:
Stefan Thurner,Medical University of Vienna, Complexity Science Hub Vienna(奥地利),圣塔菲研究所
我认为一个复杂系统在某种程度上是共演化的。元素的状态随着它们彼此之间的相互作用而变化,而相互作用又随着变化了的状态而变化。相互作用可以被认为是时效网络、超图或任何更高阶的网络。从这个意义上说,复杂系统是物理学的自然延伸,并不局限于物质和四种(实际上)永远不变的相互作用。复杂系统物理学是研究由于特定相互作用引起的随时间变化的力(可能是多个强度相似的力)的科学。复杂系统科学的本质是,一个系统在其中演化的“背景”也是共演化动力学的一部分。这可以被认为是共演化的多层网络。如果一个系统在这个意义上不是共演化的,那么它仍然属于传统物理学的范畴:在一些固定力和初始及边界条件下找到运动方程(或其它更新规则)的解,可能是复合的但不复杂。
未来二十年最大的挑战是:使主流相信复杂科学的框架可以更好地解决一些问题,并有助于理解复杂系统中宏观“因果关系”挑战所产生的基本极限。
复杂性科学是物理学未来几十年延伸发展的一个方向,2021年诺贝尔奖在这个方向的早期阶段即带来了广泛关注以及当之无愧的认可。
复杂系统是鲁棒的,但它们自身也包含着崩溃的因子。复杂系统中一个突出其“脆弱性”的特征,是其潜在的非高斯统计性质:幂律。这意味着异常值是常态而不是例外——大的且非平凡的波动比比皆是。复杂系统的崩溃通常与网络动力系统中链路(相互作用)的大规模重组事件有关。如果这个系统是有弹性韧性的,那么在某种意义上,这些链路可以重新建立起来,这样一段时间后,这个系统就可以像以前一样运行,或者可能会有所不同。
这主要来自于必须同时考虑许多自由度。为了做出好的预测,人们常常必须依赖于对微观因果相互作用的良好理解,而这种相互作用可能是难以置信的多。不断增长的可用大数据当然有所帮助。如果相互作用也是非线性的,事情就变得更具挑战性。然而,这是物理学的一个奇妙之处——存在着“普适性”,这意味着,细节对于预测集体行为的某些特征并不重要。接下来的挑战是:要知道对于一个特定系统,它是否表现出这种普适性,如果表现出这种普适性,它属于哪一个普适性类。
跨领域的优势是有机会取得比渐进式进展更大的进展。在历史上,大多数进步都发生在科学领域的边缘,而不是核心。挑战在于,为了真正做到跨学科,至少应有一名合作者对所涉领域有足够的了解。这需要卓越的训练。如果不认真对待这一点,就有可能被指责为平庸的科学家,也不会取得多大进展。确实有一些比较尴尬的例子。
我深深地崇拜获奖者,他们以自己的方式推动了对复杂系统的理解,而且方法如水晶般清晰。
我不想重新定义复杂系统,我想把重点放在复杂系统的两个独特特征上,它们与我们今天的社会生活关系更密切:“涌现”和“不可预测性”。
涌现是复杂系统的主要特征之一,它是指系统的行为不能通过单独分析其各部分的行为来解释和预测,换句话说,整体大于各部分的(线性)总和。涌现是理解我们的社会在进化过程中如何形成和变化的核心概念。在某种程度上,我们理解了形成更大群体的集体收益随着群体规模的增长非线性增长,这成为群体、部落、村庄、城镇、城市和后来的国家乃至更大的全球社会结构形成的驱动力;所以可以说,涌现行为的突出例子就是我们的社会生活。
非线性是涌现行为的数学表现形式,与复杂系统的另一个特征密切相关,即对扰动的不可预测响应。用社会科学的语言来说,这可能相当于对政策和政策变化的意外反应。例如,眼镜蛇效应就是一个很好的例子,表明一项政策通过反馈回路和非线性响应导致了意想不到的结果[56]。为了减少毒蛇的数量,启动“赏金”(bounty)计划,而且很成功。但很快,个人开始饲养蛇以获得更多奖励。当这个计划终止时,据说,蛇更多了!我相信,这就是复杂科学和复杂系统科学家们可以为政策制定提供宝贵见解的地方:提醒和警告政策制定者,他们的行为会产生意想不到的后果。总之,社会复杂系统最重要的特征是涌现行为和非线性;两者对我们的社会生活都有重大影响。
就研究领域而言,我认为复杂科学在未来20年面临的最大挑战,是理解、预测、设计和控制与生活相关的社会技术系统。由于信息和通信技术、机器人技术、人工智能、G4和即将到来的G5的进步,环境以及我们与之互动的主体的复杂性急剧增加。个人、社会和职业生活现在都嵌入到人机网络中[57]。我们与半智能机器在这些多层网络中的共存[29]自然会导致不可预测的结果[58],其中一些可能是灾难性的,如流行病或不可逆转的气候变化,而一些可能是有益的,如基于互联网的集体智慧、众包倡议[59]和公民科学项目[60]。对于复杂科学界来说,识别、研究和理解这些相互关联的社会技术环境的特征是很重要的。
在复杂系统研究的方法论和认识论方面,那些主要挑战还是为复杂系统理论寻找实验证据的日子,已经一去不复返了。我们当今社会的数字化性质自然地导致了前所未有的交易数据的产生,也就是大数据。在过去的二十年里,这些数据一直是复杂系统研究的主要材料。然而,依赖于大数据的观察性研究并没有解决相关性与因果关系这一长期存在的问题。复杂系统研究,特别是社会复杂行为研究的下一个方法论挑战,是如何设计和进行符合伦理、可扩展、同时又能指出因果关系的行为实验,帮助验证现有理论,并产生适合不断变化的社会技术系统中新观察结果的新理论。这符合除线性回归和p值分析之外更严格的统计分析的需要[61]。
>> AI奇点临近,人类社会何去何从?关注「后 ChatGPT 时代」读书会:

复杂系统科学获得诺贝尔奖的认可,对该领域的社群来说是一项巨大的成就。几年来,复杂系统研究,正如任何其他的跨学科研究,或者说反对学科化的研究领域,一直在努力确定自己在学术界的地位,获得资金和资源,并与业界和决策机构建立有意义的关系。尽管如此,复杂系统研究的认可度不断攀升,并由这次诺贝尔奖所增强,人们希望,其中一些问题在未来几年将变得不那么具有挑战性。现在需要注意的是,在公众眼中,复杂系统科学已经远远超出了仅限于观察分布或网络可视化的现象学研究。这些最初的实证观察和富有洞察力的可视化之后,复杂系统科学对机械模型[62]和真实世界含义的解释[63]有了更深的理解。复杂系统科学现在是坚实的科学,依靠科学方法来解决社会中最具挑战性的问题。
在我看来,鲁棒性和脆弱性悖论的最佳例子是自组织临界,即系统自组织到临界点,在那里出现分岔和无标度现象。在向分岔点移动时,系统是鲁棒的。在现实世界和社会科学的背景下,我们社会的自仿射组织是一种稳健的行为,然而社会组织(如社会团体、公司和城市)的稳定性并不一定是理所当然的[64]。社会结构诞生和成长背后的最初机制可以导致社会结构的衰落和毁灭。总体而言,社会组织的生态系统在临界点附近是稳定的,在临界点上,人们发现构成整体的组织之间存在分岔和无标度结构。
对这个问题的回答与上一个问题的回答有关,即根据定义,不可预测性是复杂系统的一个核心特征。然而,在实际情况中,有许多例子表明,数学建模与精确测量相结合,以及先进的计算工具大大提高了我们的预测能力。今天,飓风和其他气候灾害令我们措手不及的情况比20年、50年和100年前少得多。尽管气候行为变得更不可预测,然而随着我们对气候系统理解、用于预测天气的更精确的气象测量和超级计算机可获得性的进步,我们能够更好地避免灾难性事件。
同样,由于社交媒体的广泛使用,我们的社会政治行为变得更加“动荡”[65],然而,我们在这些平台上留下的数字足迹,结合计算工具和复杂系统方法来表征隐藏模式,有助于政策制定者理解和应对他们所代表的公民的社会需求[66]。
如前所述,与任何其他跨学科研究领域类似,复杂科学一直在努力获得学术界对其应有的认可、资助和有保障的工作,并吸引那些对复杂系统研究方向的职业机会缺乏信心的优秀学生。学术之外的主要问题,是如何将复杂科学的发现与现实世界的问题联系起来。复杂科学在某种程度上仍然停留在理论或知识层面。我们希望2021年诺贝尔奖对复杂科学的垂青,能帮助我们克服这两个问题。
诺贝尔奖的宗旨是,应该授予对人类生活产生最积极影响的研究[67]。诺贝尔奖认可复杂科学的另一方面是:希望复杂性研究社群确保复杂科学能超越智力探索,将研究结果和产生的见解转化为可以应用的指导方针和日常知识,从而在从个人到全球的各个层面上造福人类。
[1] The Nobel Prize in Physics https://www.nobelprize.org/prizes/physics/2021/summary/ (accessed 6 June 2022)
[2] Albert R and Baraba ́ si A-L 2002 Statistical mechanics of complex networks Rev. Mod. Phys. 74 47
[3] M ́ezard M, Parisi G and Virasoro M A 1987 Spin Glass Theory and Beyond: An Introduction to the Replica Method and its Applications vol 9 (Singapore: World Scientific)
[4] Manabe S and Wetherald R T 1975 The effects of doubling the CO2 concentration on the climate of a general circulation model J. Atmos. Sci. 32 3–15
[5] Hasselmann K 1976 Stochastic climate models part: I. Theory Tellus 28 473–85
[6] Pastor-Satorras R, Castellano C, Van Mieghem P and Vespignani A 2015 Epidemic processes in complex networks Rev. Mod. Phys. 87 925
[7] Kardar M, Parisi G and Zhang Y-C 1986 Dynamic scaling of growing interfaces Phys. Rev. Lett. 56 889
[8] Benzi R, Parisi G, Sutera A and Vulpiani A 1982 Stochastic resonance in climatic change Tellus 34 10–6
[9] Albert R, Jeong H and Baraba ́si A-L 2000 Error and attack tolerance of complex networks Nature 406 378–82
[10] Cohen R, Erez K, Ben-Avraham D and Havlin S 2000 Resilience of the Internet to random breakdowns Phys. Rev. Lett. 85 4626
[11] Cohen R, Erez K, Ben-Avraham D and Havlin S 2001 Breakdown of the Internet under intentional attack Phys. Rev. Lett. 86 3682
[12] Dorogovtsev S N, Goltsev A V and Mendes J F F 2008 Critical phenomena in complex networks Rev. Mod. Phys. 80 1275
[13] Battiston F et al 2021 The physics of higher-order interactions in complex systems Nat. Phys. 17 1093–8
[14] Bianconi G 2021 Higher-Order Networks: An Introduction to Simplicial Complexes (Cambridge: Cambridge University Press)
[15] Bianconi G and Baraba ́si A-L 2001 Bose–Einstein condensation in complex networks Phys. Rev. Lett. 86 5632–5
[16] Perseguers S, Lewenstein M, Ac ́ın A and Cirac J I 2010 Quantum random networks Nat. Phys. 6 539–43
[17] Biamonte J, Faccin M and De Domenico M 2019 Complex networks from classical to quantum Commun. Phys. 2 53
[18] Thurner S, Hanel R and Klimek P 2018 Introduction to the Theory of Complex Systems (Oxford: Oxford University Press)
[19] Carlson J M and Doyle J 2002 Complexity and robustness Proc. Natl Acad. Sci. USA 99 2538–45
[20] Quantum@ccs2022: satellite conference ‘complex systems: quantum information and computation’
https://quantumccs2022.ifisc.uib-csic.es/ (accessed 14 June 2022)
[21] Sundar B, Walschaers M, Parigi V and Carr L D 2021 Response of quantum spin networks to attacks J. Phys. Complex. 2 035008
[22] Walschaers M, Treps N, Sundar B, Carr L D and Parigi V 2020 Emergent complex quantum networks in continuous-variables non-Gaussian states (arXiv:2012.15608)
[23] Hillberry L E, Jones M T, Vargas D L, Rall P, Halpern N Y, Bao N, Notarnicola S, Montangero S and Carr L D 2021 Entangled
quantum cellular automata, physical complexity, and goldilocks rules Quantum Sci. Technol. 6 045017
[24] Jones E B et al 2022 Small-world complex network generation on a digital quantum processor Nat. Commun. 13,1–7
[25] Page S 2010 Diversity and Complexity (Princeton, NJ: Princeton University Press)
[26] Complexity article in Wikipedia https://en.wikipedia.org/wiki/Complexity (accessed 8 May 2022)
[27] Kauffman S A 2019 A World Beyond Physics: The Emergence and Evolution of Life (Oxford: Oxford University Press)
[28] Battiston F, Cencetti G, Iacopini I, Latora V, Lucas M, Patania A, Young J-G and Petri G 2020 Networks beyond pairwise
interactions: structure and dynamics Phys. Rep. 874 1–92
[29] Bianconi G 2018 Multilayer Networks: Structure and Function (Oxford: Oxford University Press)
[30] Dehmamy N, Milanlouei S and Baraba ́si A-L 2018 A structural transition in physical networks Nature 563 676–80
[31] Yadav S P, Prasad Mahato D and Linh N T D 2020 Distributed Artificial Intelligence: A Modern Approach (Boca Raton, FL: CRC Press)
[32] Nobel Lectures in Physics 2021 https://nobelprize.org/prizes/physics/2021/hasselmann/lecture/ (accessed 8 May 2022)
[33] Nobel Lectures in Physics 2021 https://nobelprize.org/prizes/physics/2021/manabe/lecture/ (accessed 8 May 2022)
[34] Nobel Lectures in Physics 2021 https://nobelprize.org/prizes/physics/2021/parisi/lecture/ (accessed 8 May 2022)
[35] Buldyrev S V, Parshani R, Paul G, Stanley H E and Havlin S 2010 Catastrophic cascade of failures in interdependent networks Nature 464 1025–8
[36] Wachs J, Yasseri T, Lengyel B and Kert ́esz J 2019 Social capital predicts corruption risk in towns R. Soc. Open Sci. 6 182103
[37] Reich N G et al 2022 Collaborative hubs: making the most of predictive epidemic modeling Am. J. Public Health e1–4
[38] Arrhenius S 1896 On the influence of carbonic acid in the air upon the temperature of the ground London, Edinburgh Dublin Phil. Mag. J. Sci. 41 237–76
[39] Bjerknes V 1904 Das Problem der Wettervorhersage, betrachtet vom Standpunkte der Mechanik und der Physik Meteorol. Z. 211–7
[40] Richardson L F 1922 Weather Prediction by Numerical Process (Cambridge: Cambridge University Press)
[41] Manabe S and Stouffer R J 1980 Sensitivity of a global climate model to an increase of CO2 concentration in the atmosphere J. Geophys. Res. 85 5529–54
[42] Maier-Reimer E and Hasselmann K 1987 Transport and storage of CO2 in the ocean—an inorganic ocean-circulation carbon cycle model Clim. Dyn. 2 63–90
[43] Cubasch U, Hasselmann K, Ho ̈ck H, Maier-Reimer E, Mikolajewicz U, Santer B D and Sausen R 1992 Time-dependent
greenhouse warming computations with a coupled ocean-atmosphere model Clim. Dyn. 8 55–69
[44] Watts D J 2011 Everything Is Obvious: Once You Know the Answer (New York: Crown Business) 27 J.Phys.Complex. 4 (2023) 010201 (28pp) Editorial
[45] Dijkstra H A, Herna ́ndez-Garc ́ıa E, Masoller C and Barreiro M 2019 Networks in Climate (Cambridge: Cambridge University Press)
[46] Boers N, Goswami B, Rheinwalt A, Bookhagen B, Hoskins B and Kurths J 2019 Complex networks reveal global pattern of extreme-rainfall teleconnections Nature 566 373–7
[47] Motter A E 2015 Networkcontrology Chaos 25 097621
[48] Yang Y, Nishikawa T and Motter A E 2017 Small vulnerable sets determine large network cascades in power grids Science 358 eaan3184
[49] Cornelius S P, Kath W L and Motter A E 2013 Realistic control of network dynamics Nat. Commun. 4 1942
[50] Gray K A and Motter A E 2018 Multidisciplinary Complex Systems Research: Report from an NSF Workshop in May 2017 available at: https://bit.ly/2Jg3sSE
[51] Wikner A, Pathak J, Hunt B R, Szunyogh I, Girvan M and Ott E 2021 Using data assimilation to train a hybrid forecast system that
combines machine-learning and knowledge-based components Chaos 31 053114
[52] GuimeraR,ReichardtI,Aguilar-MogasA,MassucciFA,MirandaM,PallaresJandSales-PardoM2020ABayesianmachine scientist to aid in the solution of challenging scientific problems Sci. Adv. 6 eaav6971
[53] Fajardo-Fontiveros O, Reichardt I, Rios H R, Duch J, Sales-Pardo M and Guimera R 2022 Fundamental limits to learning closed-form mathematical models from data (arXiv:2204.02704)
[54] Anderson P W 1972 More is different Science 177 393–6
[55] Parisi G 1999 Complex systems: a physicist’s viewpoint Physica A 263 557–64
[56] Manheim D and Garrabrant S 2018 Categorizing variants of Goodhart’s law (arXiv:1803.04585)
[57] Tsvetkova M, Yasseri T, Meyer E T, Pickering J B, Engen V, Walland P, L ̈uders M, Følstad A and Bravos G 2017 Understanding human-machine networks: a cross-disciplinary survey ACM Comput. Surv. 50 1–35
[58] Tsvetkova M, Garc ́ıa-Gavilanes R, Floridi L and Yasseri T 2017 Even good bots fight: the case of Wikipedia PLoS One 12 e0171774
[59] Yasseri T and Menczer F 2021 Can crowdsourcing rescue the social marketplace of ideas? (arXiv:2104.13754)
[60] Ibrahim K, Khodursky S and Yasseri T 2021 Gender imbalance and spatiotemporal patterns of contributions to citizen science projects: the case of zooniverse Front. Phys. 9 650720
[61] Vidgen B and Yasseri T 2016 P-values: misunderstood and misused Front. Phys. 4 6
[62] Holme P and Liljeros F 2015 Mechanistic models in computational social science Front. Phys. 3 78
[63] Watts D J 2017 Should social science be more solution-oriented? Nat. Human Behav. 1 0015
[64] West G 2018 Scale: The Universal Laws of Life, Growth, and Death in Organisms, Cities, and Companies (London UK: Penguin)
[65] Margetts H, John P, Hale S and Yasseri T 2015 Political Turbulence (Princeton, NJ: Princeton University Press)
[66] Vidgen B and Yasseri T 2020 What, when and where of petitions submitted to the UK government during a time of chaos Policy Sci. 53 535–57
[67] Shalev BA 2002 100 years of Nobel prizes (Los Angeles:CA, The Americas Group)
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「我的集智」推送论文信息。扫描下方二维码即可一键订阅:





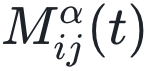 来描述,元素状态可以用含时函数
来描述,元素状态可以用含时函数