关键词:湍流,物理启发的深度学习,数值模拟,小尺度动力学
论文标题:Forecasting small-scale dynamics of fluid turbulence using deep neural networks
斑图链接:https://pattern.swarma.org/paper/b610e95c-2691-11ee-a79c-0242ac17000d
论文地址:https://www.pnas.org/doi/10.1073/pnas.2305765120
湍流的特点是在空间和时间的广泛相互作用尺度上出现强烈而混乱的波动。这种多尺度相互作用是高度非线性的,导致控制方程在数学上难以处理。由于这种尺度范围随着流体雷诺数(Reynolds number)的幂次增加,因此在高雷诺数下对整个尺度范围进行精确模拟的成本极高。模拟最昂贵的部分涉及小尺度运动;因此,研究的关键在于利用小尺度运动的假定普遍性,重点是理解小尺度运动并对其进行建模。
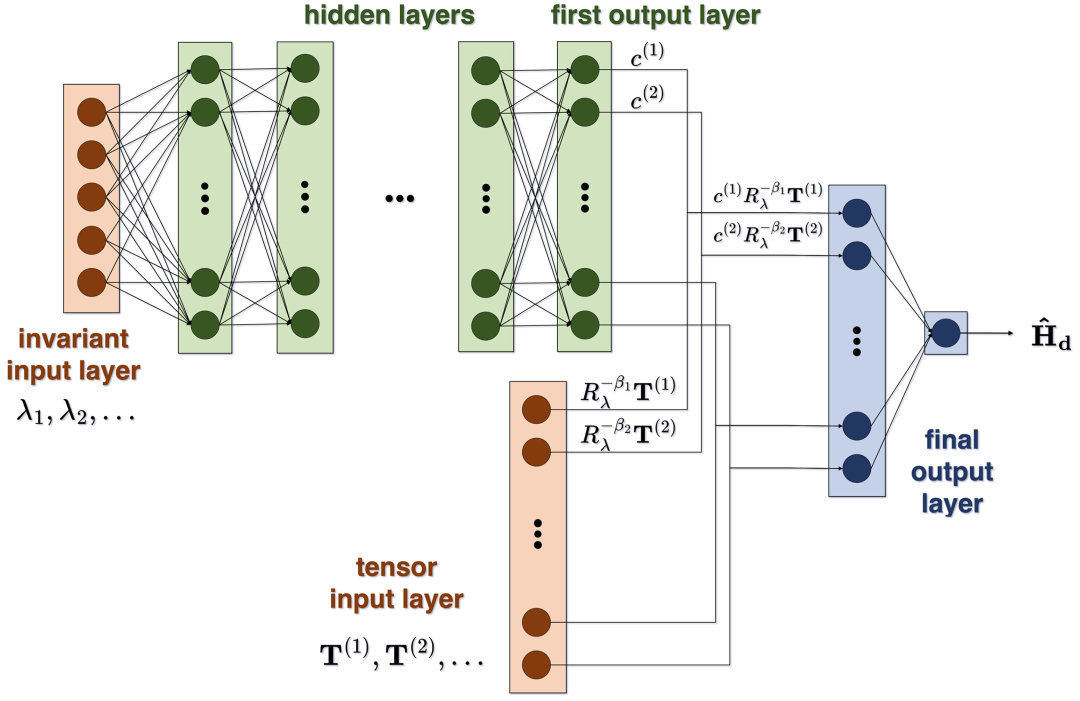
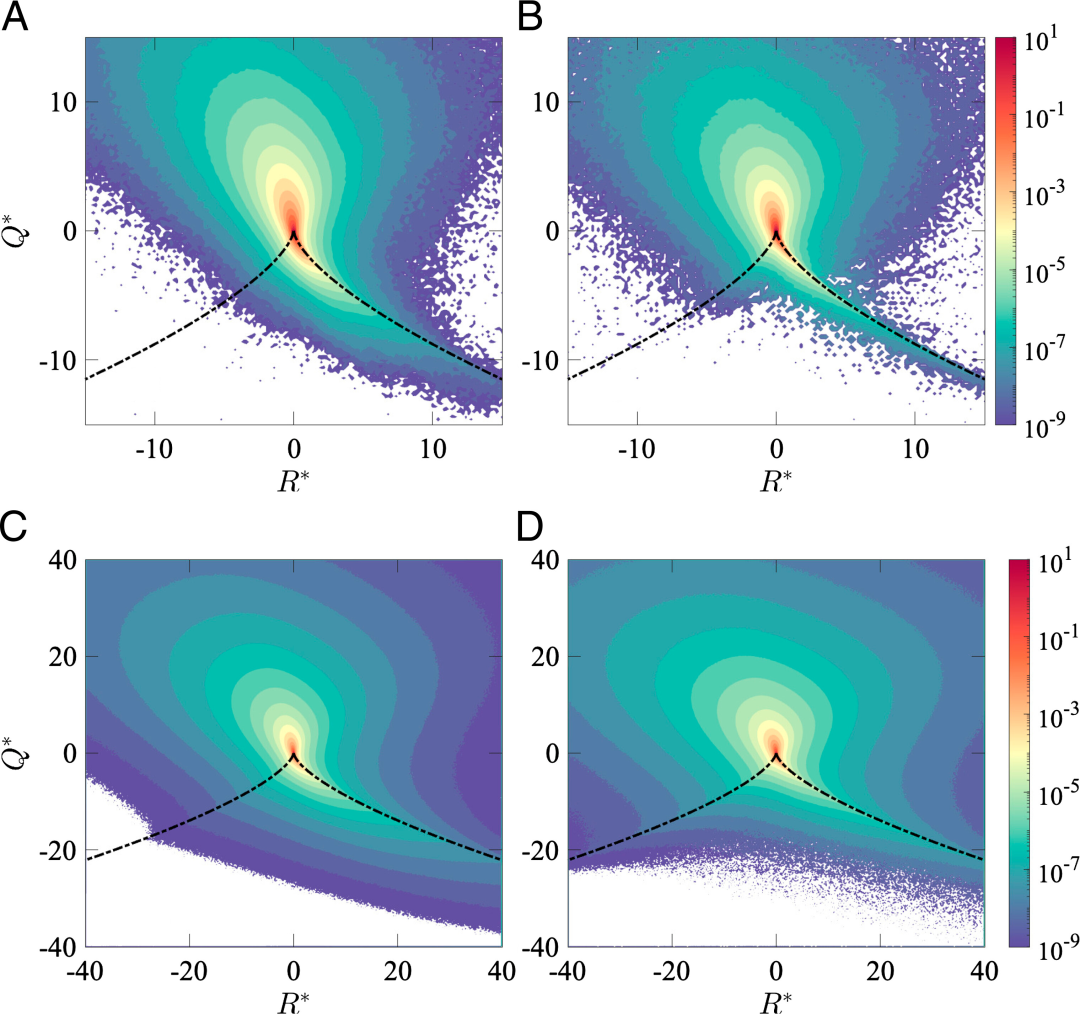
在这篇最新发表于PNAS的文章中,作者使用物理启发的深度学习方法,提出了一个建模框架,通过速度梯度张量(velocity gradient tensor)来捕捉和预测湍流的小尺度动力学。该模型基于获取压强 Hessian 矩阵和粘性拉普拉斯函数作为速度梯度张量的函数闭包。这项任务利用符合物理约束条件的深度神经网络完成,该网络明确纳入了雷诺数依赖性,以考虑小尺度间歇性。然后,作者使用一个包含两个数量级的大尺度雷诺数的大型直接数值模拟数据库进行训练和验证。模型从低到中等雷诺数进行深度学习,并成功预测在已见和未见的更高雷诺数下的速度梯度统计。这篇文章的方法成功表明,深度学习在捕捉和预测湍流的小尺度特征方面,比传统的建模方法更具有可行性。
图1. Reynolds数标度的基于张量的神经网络(ReS-TBNN)架构用于建模偏差压强 Hessian。
图2. 比较速度梯度张量不变量的联合概率密度函数的模拟结果。
图3. 在ReS-TBNN模型对压力Hessian和粘性Laplacian项进行训练时,损失函数的衰减。
推荐阅读