关键词:复杂时空动力学,偏微分方程,物理启发机器学习,深度学习,反应-扩散过程
论文标题:Encoding physics to learn reaction-diffusion processes
论文来源:Nature Machine Intelligence
斑图链接:https://pattern.swarma.org/paper/e3d0cc1a-24f5-11ee-931d-0242ac17000d
原文链接:https://www.nature.com/articles/s42256-023-00685-7
复杂的时空动力系统,如反应-扩散(Reaction–diffusion, RD)过程,可以在各学科的许多基本动力学效应中找到,对其建模主要依赖于找到基本偏微分方程(PDEs)。然而在许多情况下,由于先验知识不足以及缺乏描述系统变量非线性过程的明确的偏微分方程公式,预测这些系统的演变会是一项具有挑战性的任务。
用最新的数据驱动方法,可以从测量数据中学习,同时增加先验物理知识。然而,现有的物理启发机器学习(physics-informed machine learning)范式通过软惩罚约束强加了物理定律,而解的质量在很大程度上取决于超参数的试错式适当设置。
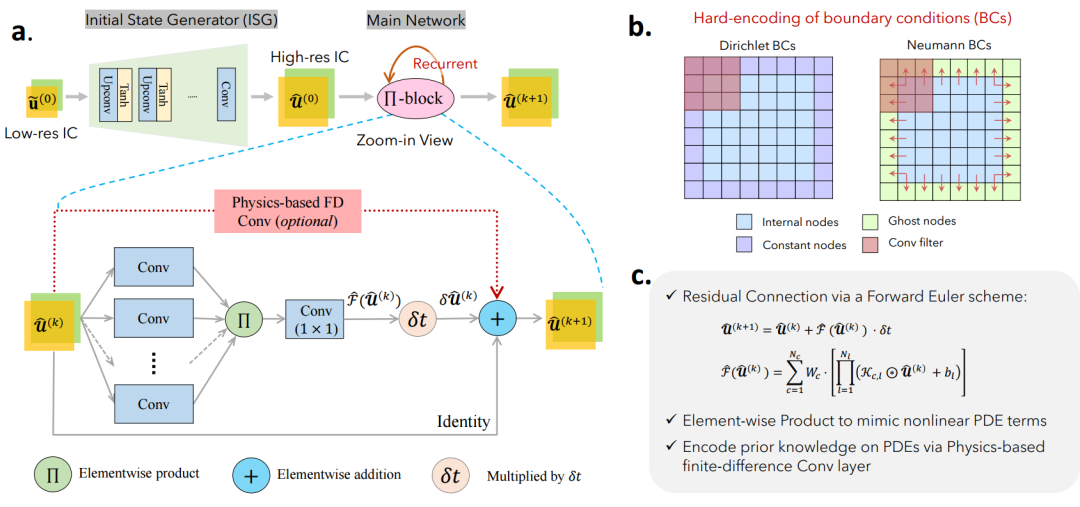
文章提出一种深度学习框架——物理编码递归卷积神经网络(physics-encoded recurrent convolutional neural network, PeRCNN),能在递归卷积神经网络中对给定的物理结构强制编码,从而促进稀疏数据环境下的时空动力学学习。该网络旨在保留给定物理结构,例如控制PDE、IC和边界条件(BC)的结构或特定项,先验物理知识被强制“编码”,从而使网络具有可解释性。
图1:PeRCNN结构示意图:a. 带有用于递归计算的Π块的网络;b. BC的嵌入;以及 c. 网络的主要特征
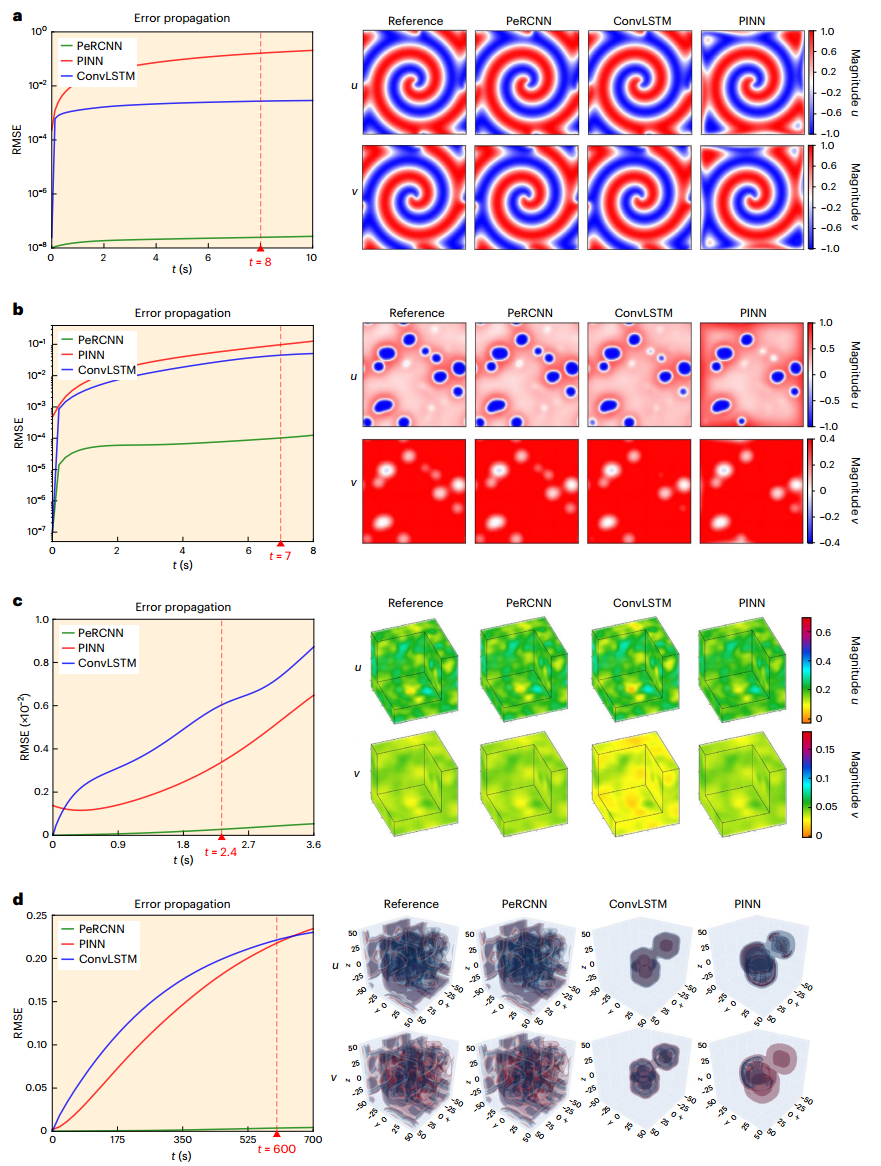
由图2可见,在四种情况下PeRCNN得到的解与参考解都非常吻合,相比之下,卷积长短期记忆(convolutional long-short term memory, ConvLSTM)和物理启发神经网络(physics-informed neural networks, PINN)在二维、三维上的表现就不同了。特别是,它们对二维情况的预测相当准确,而但对三维情况的预测与参考值有相当大的偏差。证明PeRCNN在复杂系统建模和仿真方面的巨大潜力。
图2:PeRCNN、ConvLSTM和PINN在各种RD系统上的误差传播曲线(左)和预测快照(右)。a,二维lambda–omega (λ–Ω) RD方程;b,二维FitzHugh–Nagumo (FN) RD方程;c,三维FN RD方程;d,三维Gray–Scott (GS) RD方程
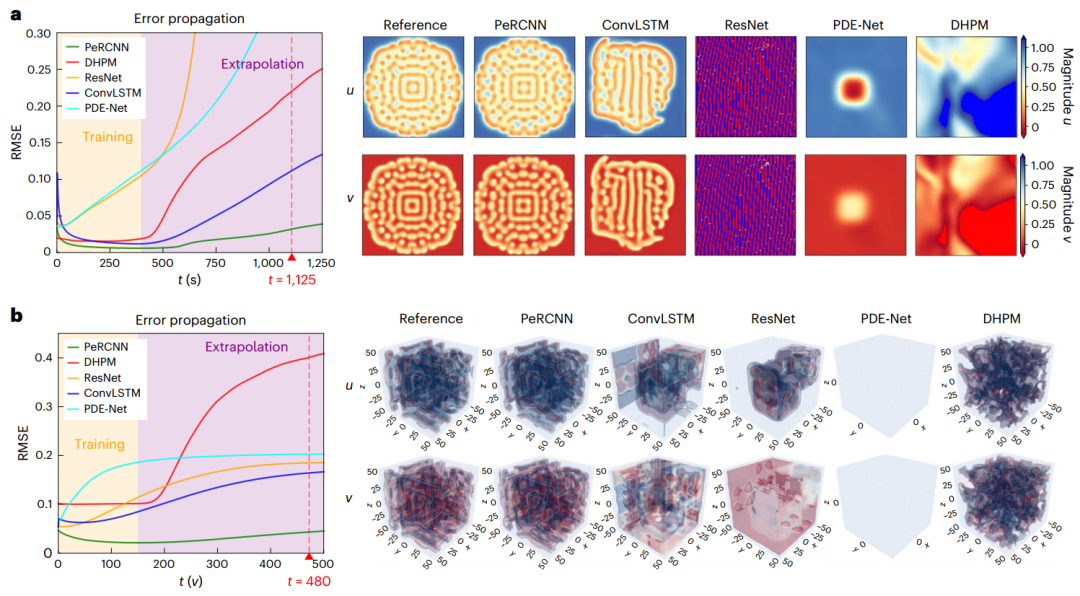
接下来关注在有限的、有噪声的测量数据条件下,利用所提出的物理编码学习范式建立时空动力学数据驱动模型。由图3可见,在误差传播的各个阶段,PeRCNN的表现都优于其他方法,进一步证实了PeRCNN的外推能力。
图3:每个数据驱动模型的预测(左)和外推快照(右)与参考解相比的误差传播曲线。a,二维GS RD方程;b,三维GS RD方程
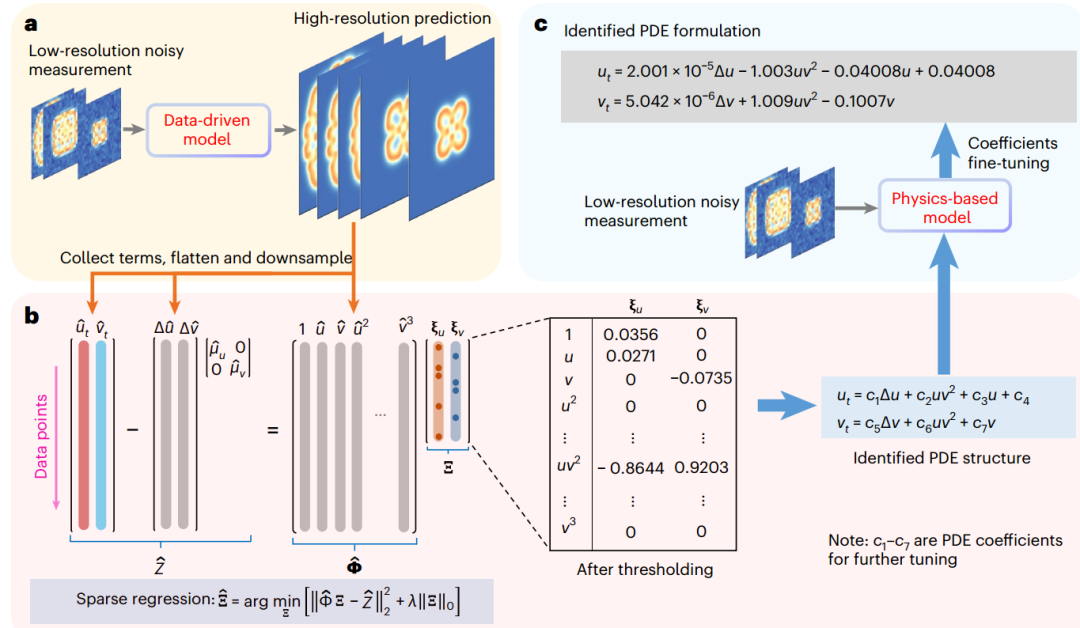
最后,将从数据中学到的模式转化为知识,从而引导科学家理解物理变量之间的因果关系,并进一步对类似问题进行推理,基于此,作者尝试将稀疏回归技术与PeRCNN模型相结合,如图4所展示。
图4 控制PDE的流畅图。a,数据重构;b,稀疏回归;c,系数微调
作者通过大量数值实验展示了所提出的方法如何应用于有关反应扩散过程和其他PDE系统的各种问题,包括PDE的正演和反演分析、数据驱动建模和发现。证明PeRCNN具有高准确性、鲁棒性、可解释性和可泛化性。
推荐阅读