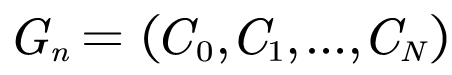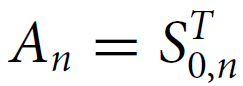前沿进展：高阶网络中的团排序

导语

复杂网络中的关键节点对于网络动力学具有重要影响。比如在真实网络中，阻断传播源可以有效控制流行病蔓延，提高基础设施韧性有助于防止级联失效。近日发表于 Chaos 的一项最新研究将节点排序研究扩展到高阶相互作用网络中，提出了几种量化指标对高阶网络中的团进行排序。结果表明，这些指标能有效降低大规模网络的维数，更准确地找到重要团。

研究领域：复杂网络，高阶网络，团排序，网络动力学，同步，流行病传播

朱欣怡 | 作者

论文题目：

Ranking cliques in higher-order complex networks

论文链接：

https://pubs.aip.org/aip/cha/article/33/7/073139/2903051/Ranking-cliques-in-higher-order-complex-networks

微博红人和微博新人的“公众”影响力一样吗？脑神经网络中每个神经元同等重要吗？交通网络中每个城市对全国交通的连通性都做出了同等的贡献吗？

在异质网络中，每个节点的重要性都不一样，排序就是把节点按重要性高低排成一列，可以帮助我们识别出“最重要”的节点。在不同粗粒化的视角里，节点的重要性排序也不尽相同。人们在不同的研究问题中使用着不同的排序方法。

传统的网络分析局限于只有两两交互的节点的复杂网络表示。然而，在大量研究中，网络中的相互作用并不局限于节点对，常常涉及到节点的高阶团（clique）。研究团之间的高阶互动，我们需要新指标、新工具。对团进行排序有助于理解具有高阶结构的大规模复杂网络中更多的涌现动力学现象，比如同步、动力学演化和流行病传播等重要问题。

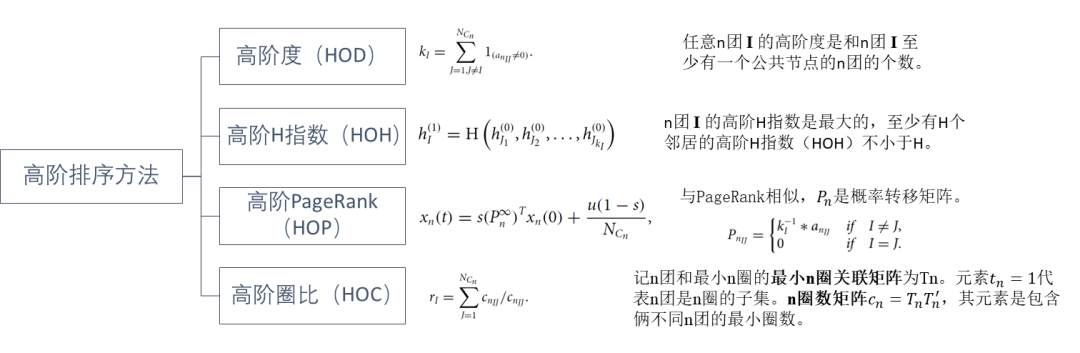
这篇文章总结了常见的几种传统节点排序方法，然后还基于拓扑单纯形提出了几种高阶中心性：高阶圈比（HOC）、高阶度（HOD）、高阶H指数（HOH）和高阶 PageRank（HOP），对团的重要性进行量化和排序，并展示了在生成网络和真实网络中的实验结果。这些结果都表明，与其他传统网络指标相比，这些高阶中心性可以将团排列得更有“区别”，能有效降低大规模网络的维数，更准确地找到重要团。更重要的是，根据所提出的度量对团进行排序，能够准确反映网络在结构鲁棒性、行为同步和动态传播等方面的功能影响。

1. 传统节点排序方法

传统的网络分析中，已经有很多根据网络性质确定网络中节点排序的方法。比如说度中心性、局部中心性、半局部算法（ClusterRank）和H指数等方法。这些方法大多使用节点的局部信息作为对节点进行排序的主要依据。这种方法有较低的计算复杂度，但是排名的信息可能不够。还有许多有效的迭代优化技术，强调节点的重要性同时受到邻居和自身的影响（相互增强效应）。此类典型的指标包括：特征向量中心性、PageRank、LeaderRank、圈比（cycle ratio）等等。

关于圈的介绍详见：《网络中的圈结构》

表1. 几种低阶中心性度量。

然而，上述研究节点重要性的方法都存在一定的局限性，即无法对大规模复杂网络中普遍存在的高阶交互进行研究。

2. 基于单纯形的高阶排序方法

这篇最新发表于 Chaos 的文章基于拓扑单纯形提出了几种高阶中心性：高阶圈比（HOC）、高阶度（HOD）、高阶H指数（HOH）和高阶PageRank (HOP)，对团的重要性进行量化和排序。

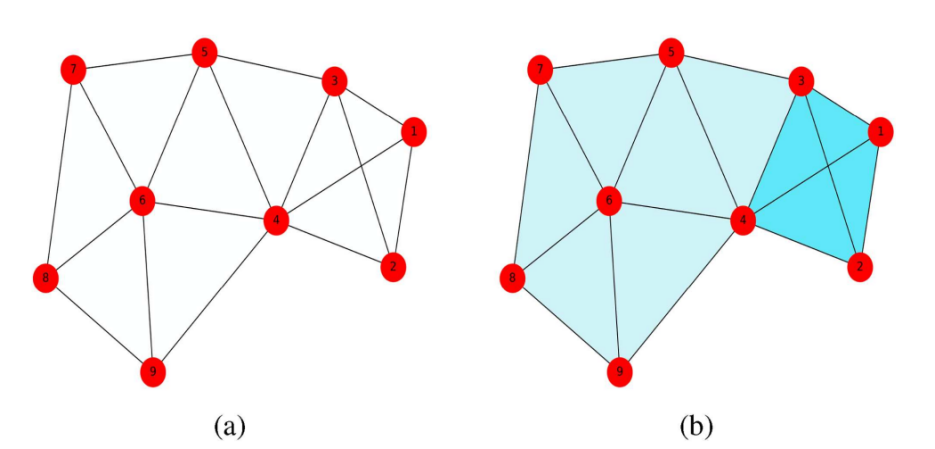
团（clique）是网络中具有特定顺序的完全子图。p团（p-clique）由p+1个完全联通的节点组成，而且这p+1个节点的所有子集都包含在p团中。其中具有N个节点的子集叫做p团中的N_sub面(N_sub-face)。所有的p面组成p团的边界。

单纯形网络（Simplicial network）定义为：

其中C₀表示节点（0团），C₁表示连边（1团），C_n表示n团。

记N_cn为n团的个数。

p,q 团间关联矩阵（incidence matrix between a p-clique and a q-clique）S_{p, q}（p<q）矩阵的大小为N_cp×N_cq，其中元素S_p, q=1代表p是q的子集，否则p不是q的子集。

n团的邻接矩阵（adjacency matrix of the n-clique）

图1. 低阶网络（a）与高阶网络（b）的示意图。

图2. 几种高阶中心性对团的重要性进行量化和排序。

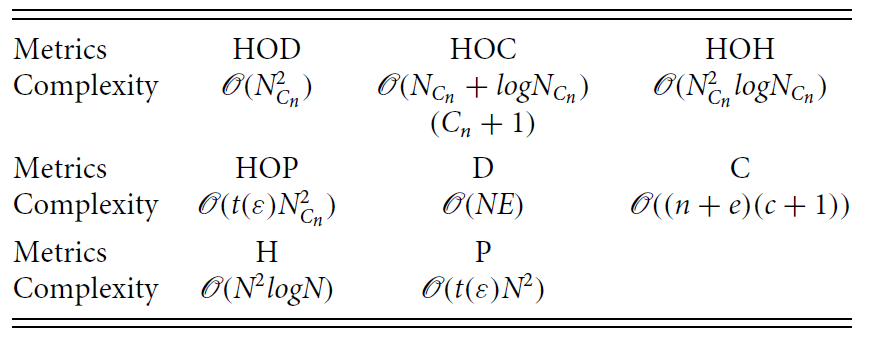
表2. 各指标的时间复杂度分析。其中t(ε)为迭代次数，与收敛的阈值ε有关。

3. 结果比较

作者在合成网络和真实网络上的实验都表明，与其他传统网络指标相比，这些高阶中心性可以将团排列得更有区别，能有效降低大规模网络的维数，能更准确地找到重要团。

什么样的团算重要呢？核心思想是“破坏性检验出重要性”。他们在实验中用团维持网络连通性、便于同步和控制传播的能力来衡量团的重要性。

真实网络鲁棒性分析

按每种方法对网络中的节点进行排序，从网络中去掉“排序最前”的团。系统崩溃得越快（即网络鲁棒性R较低），说明去掉的团越重要。

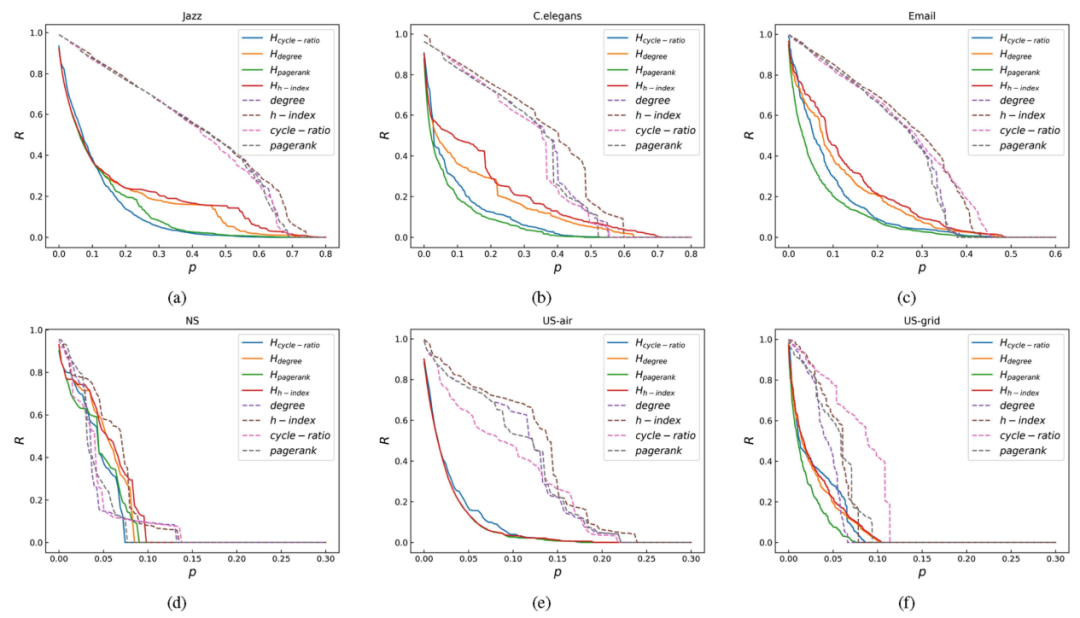
图3. 八个指标在真实网络中的渗流性能。y轴表示去除团（节点）后的网络鲁棒性，x轴表示去除团（节点）的比例。

如图3所示，随着节点一个接一个地从网络中移除，这些真实网络的鲁棒性持续下降。可以看到，在所有真实网络中，HOC和HOP曲线都位于其他曲线的底部；即当移除相同数量的节点时，HOC和HOP度量对网络的鲁棒性有显著影响。

真实世界网络的同步分析

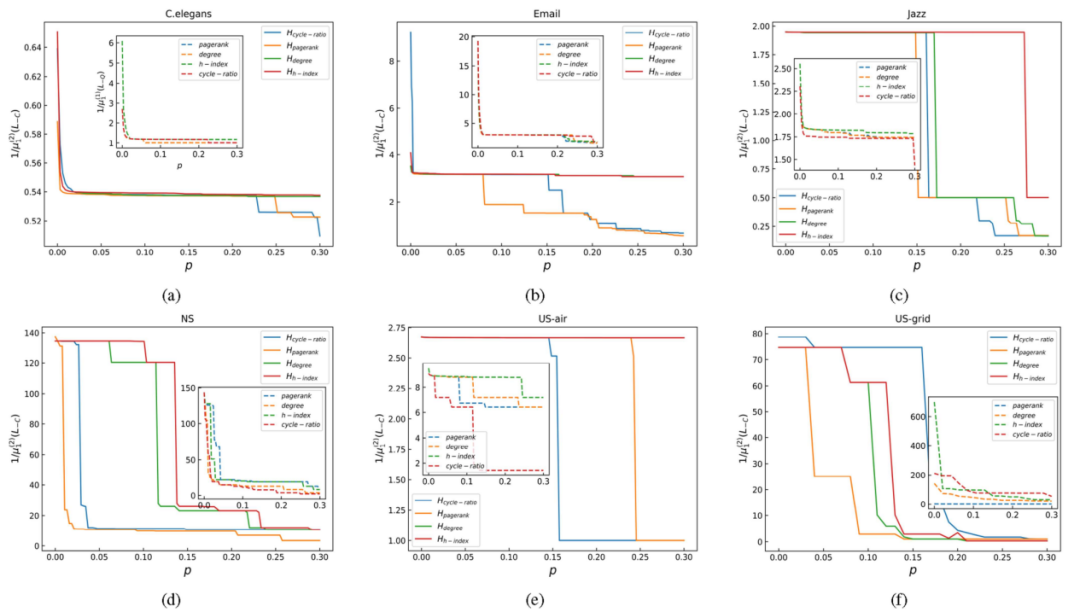
图4显示了网络的同步性如何随着固定节点（团）比例p的增加而降低。由于关键结构对网络的同步性有重大影响，作者将前30%的团固定在网络中，发现当p大于30%时，并不影响结果和结论。在图2中，更快的衰减对应更好的同步性能。

图4. 八个指标在真实网络中的同步性能。y轴表示钉住一小部分团（节点）后的网络同步，x轴表示钉住的团（节点）的比例。

由图4，作者分析出，对于所模拟的真实网络，低阶度量的影响并不能很好地区分重要结构，但高阶度量可以。

真实网络流行病传播分析

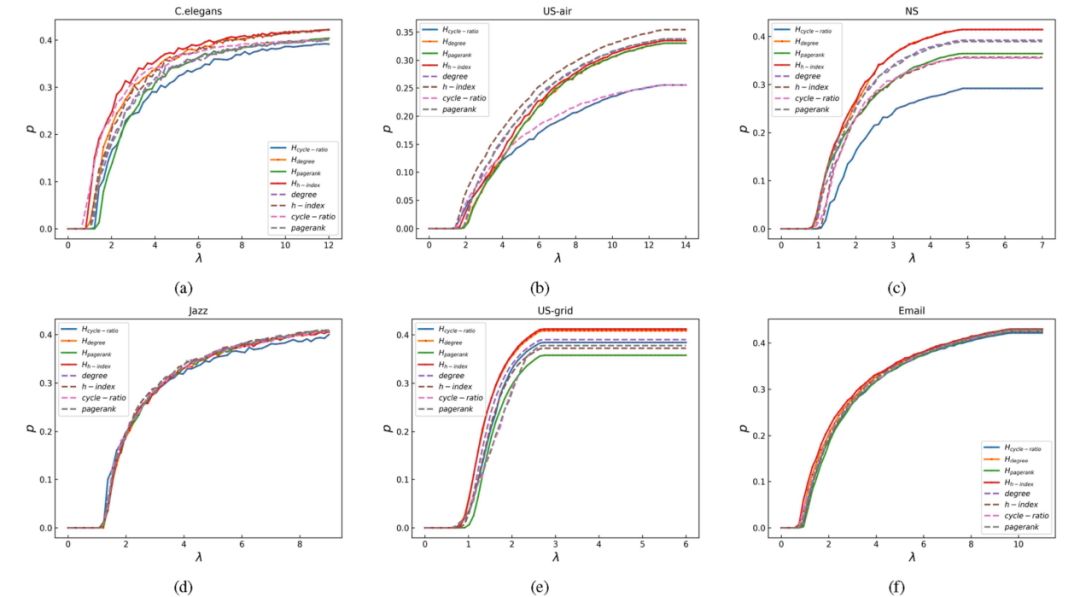
为了衡量各指标对团排序的效率，作者采用SIS模型模拟团排序对病毒传播的影响。按顺序从网络中选择排序的小团体进行免疫。网络的参数p是指稳态时，受感染节点的数量的比例。高的传播阈值和低的p值对应着良好的性能。作者对100个网络实现进行了所有模拟，然后考虑它们的平均值。

图5. 每一衡量标准对传染病在真实网络中传播的影响。y轴表示节点免疫后处于稳态的感染节点比例，x轴表示感染概率的缩放。

生成网络上的表现

真实网络的结构具有特殊性，不能代表网络的一般特征。作者选择不同参数的合成BA和ER单纯形网络来探讨所提出的度量的影响与网络拓扑之间的关系。在BA和ER单纯形网络中，重要节点的识别相对容易，而关键团的识别则比较困难。

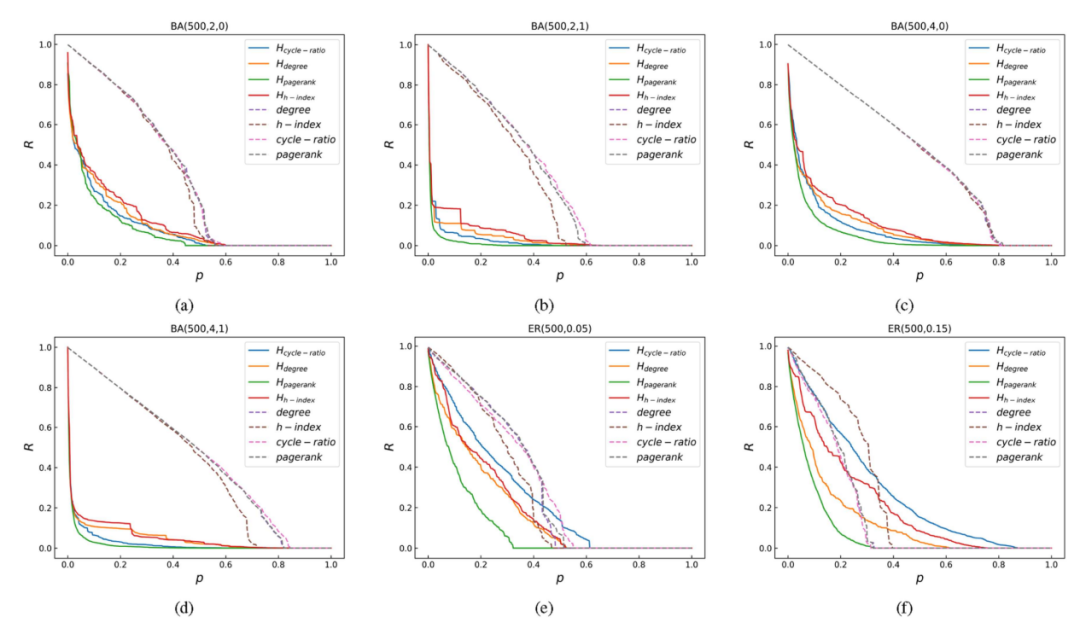
图6. 八个指标在生成网络中的渗流性能。y轴表示去除团（节点）后的网络鲁棒性，x轴表示去除团（节点）的比例。

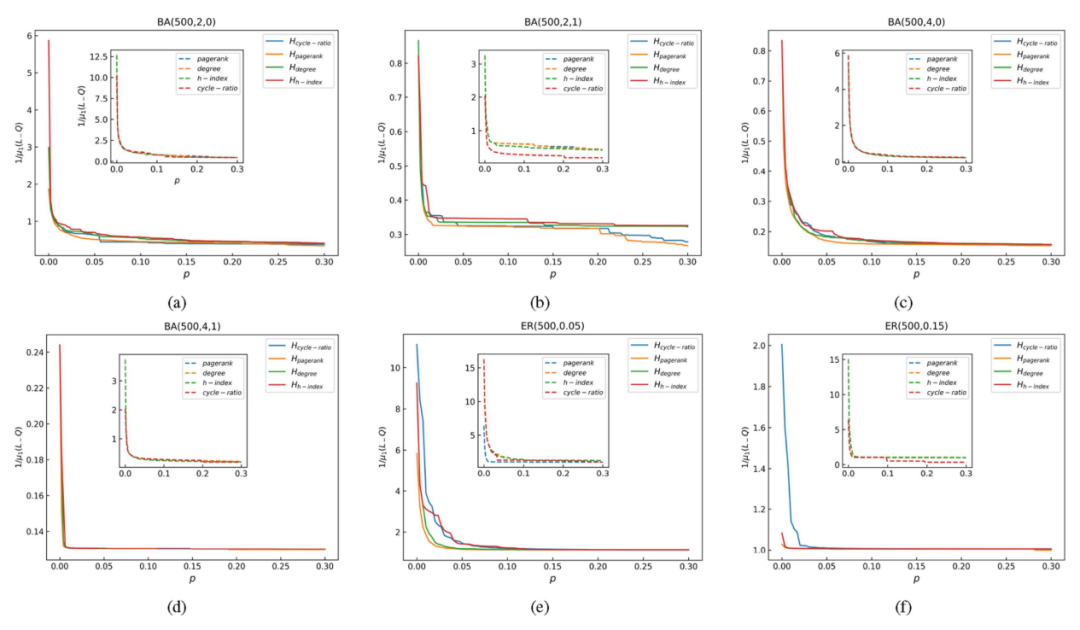
图7. 八个指标在生成网络中的同步性能。y轴表示钉住一小部分团(节点)后的网络同步，x轴表示钉住的团(节点)的比例。

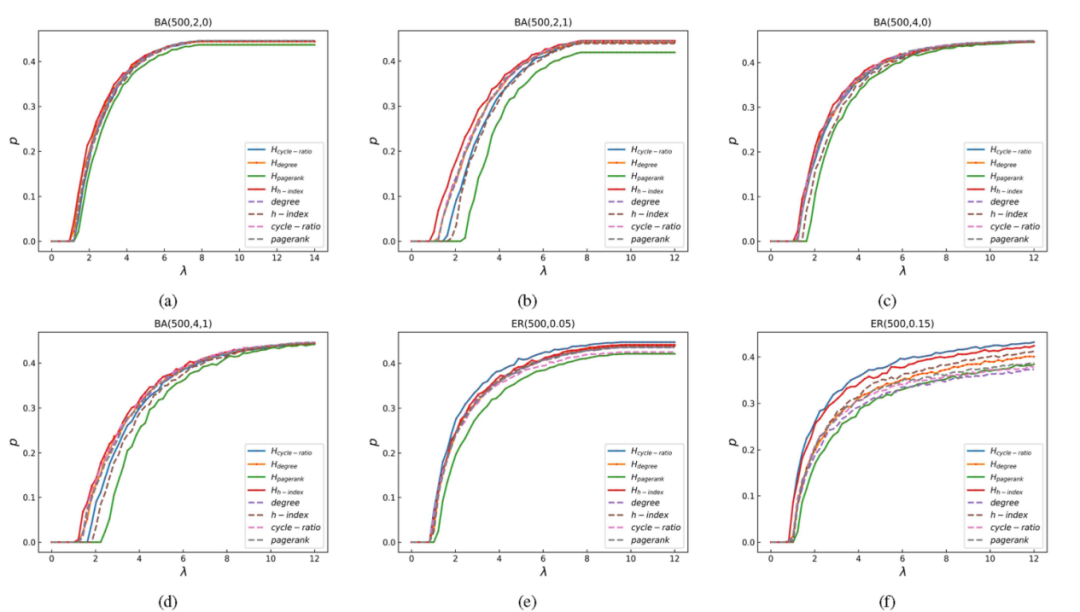
图8. 每一衡量标准对传染病在生成网络中传播的影响。y轴表示节点免疫后处于稳态的感染节点比例，x轴表示感染概率的缩放。

高阶网络社区

随着对现实世界探索的不断深入，人们发现在许多真实的复杂系统中，组成系统的个体之间不仅存在二元交互关系，也广泛存在多个体同时（或以特定顺序）进行交互，即高阶交互现象。为此，研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型，为复杂网络分析和研究提供了新的思路。

由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学（北京）管青老师在集智俱乐部联合发起了【高阶网络读书会】。读书会围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨，按照「基础理论」+「深入理论」+「案例研讨」的模式展开。读书会第一季已经圆满结束，第二季正在筹备中。现在报名加入可以解锁第一季全部录播视频并加入社群交流。