Nature计算科学最新:统计物理x机器学习用于求解组合优化问题
导语
组合优化问题(COPs)在科学和工业领域无处不在,从物流调度到芯片设计,从社交网络分析到人工智能算法,其高效求解一直是研究热点。然而,传统方法往往受限于问题的复杂性和计算资源。近日,中国科学院理论物理研究所的张潘研究员及其博士生沈子松,新加坡科技设计大学助理教授潘峰、国科大杭州高等研究院博士生门一丁、硕士生徐闻彪与合作者们在《Nature Computational Science》发表了一项突破性研究,该研究将统计物理学中的自由能最小化方法原理、平均场理论、模拟退火思想与机器学习中的自动微分与梯度优化技术相结合,提出了一种名为“自由能机器”(Free-Energy Machine, FEM)的新方法,FEM支持在GPU/FPGA等大规模并行计算设备运行,通过自由能最小化、自动微分和梯度下降三个步骤,实现了组合优化问题的统一高效求解。实验结果表明,FEM在最大割问题、平衡最小割问题和最大K-SAT问题等多个问题上表现优异,在速度和性能上超越了多个针对单一问题定制的最先进算法,同时结果也展示了其在处理组合优化领域的多值状态和多体相互作用问题上的优越性能。该研究充分证明,统计物理学与机器学习的跨学科融合,为开发具有广泛科学影响和工业应用前景的尖端方法论开启了新的可能。
关键词:组合优化、统计物理、机器学习、高性能计算
曾利丨作者
蒲天乐丨译者

论文题目:Free-energy machine for combinatorial optimization
论文链接:https://www.nature.com/articles/s43588-025-00782-0
代码链接:https://github.com/Fanerst/FEM
一、组合优化:数字时代的“高精尖”难题
一、组合优化:数字时代的“高精尖”难题
组合优化问题(COPs)普遍存在于统计物理、运筹学和人工智能等多个领域,也被公认为数字时代的“高精尖”难题。由于大多数COPs属于NP-hard问题,带来了巨大的计算挑战。除非NP=P的假设成立,否则精确算法难以提供高效解决方案。因此,模拟退火和各种局部搜索算法等经典近似算法在实践中被广泛采用。值得注意的是,这些算法主要基于串行计算,专为CPU设计。虽然某些具有特殊结构的问题可以高效求解,但大多数实际难题仍难以用标准工具解决。
近年来,随着GPU和FPGA等大规模并行计算能力的显著提升,人们对创新方法的期待与日俱增,已有许多新方法被开发出来。例如模拟相干伊辛机、噪声平均场退火和模拟分岔机等算法,这些算法最初受启发于对伊辛机硬件设备的平均场动力学模拟,其性能甚至超越了硬件原型。除了高精度优势外,这些算法的显著特点是能同步更新变量,从而有效利用GPU和FPGA加速大规模问题求解。

然而这些算法主要局限于二次无约束二值优化(QUBO)问题或伊辛模型。当处理具有非二次(如布尔k可满足性问题的高阶p自旋玻璃模型)或非二值特征(如Potts玻璃、着色问题和社区检测)的COPs时,这一局限性尤为明显。将这些复杂问题结构适配到伊辛模型需要额外的转换步骤和可观的开销,使得优化问题更加复杂难解。那么能否开发一种既保持物理模型的高效性,又能直接处理复杂约束的通用框架?
二、物理启发的创新:
自由能机器FEM的设计哲学
二、物理启发的创新:
自由能机器FEM的设计哲学
张潘老师团队所提出的Free-Energy Machine从统计物理角度出发,旨在满足组合优化问题求解在通用性、性能和速度方面的需求。该方法区别于现有技术的关键在于,无需依赖伊辛模型即可求解通用COPs。图1展示了该算法的详细流程图。
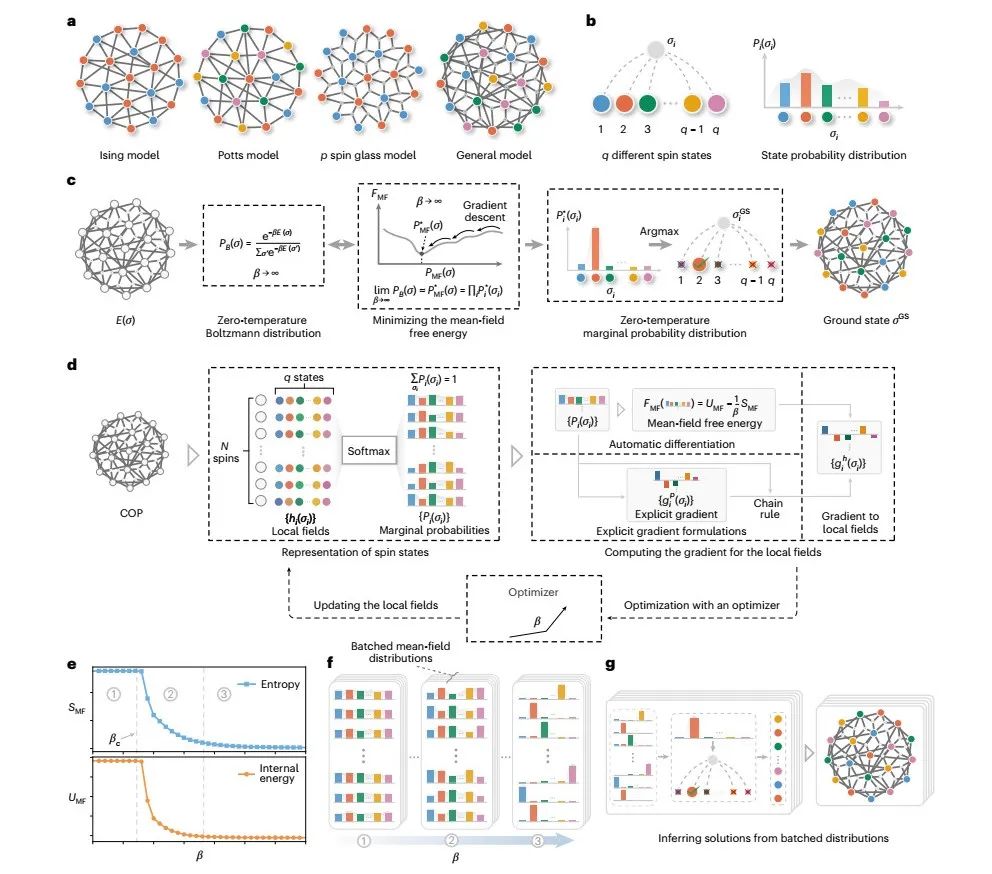
图1. FEM解决组合优化问题(COPs)的原理与框架。a图展示FEM可以解决的四种不同类型的COPs问题,即伊辛模型, 波茨模型,p-自旋玻璃模型和通用模型; b图展示,在通用COPs中,每个自旋变量σᵢ可处于q种不同状态(标记为1, 2, …, q),其状态概率由边缘概率Pᵢ(σᵢ)表示。彩色条形图直观展示各状态概率分布; c图:通过变分自由能最小化逼近基态解的过程;d图为FEM的核心计算框架,包括了局部场参数化、概率转换、梯度计算和并行优化四个步骤;e图展示了在退火过程中能量与熵的演化情况;f图展示了边缘概率{Pᵢ(σᵢ)}在退火过程中呈现出的三阶段的演化特征:①高温阶段(β较小),熵主导,概率均匀分布,②临界阶段(β≈βc)时,能量开始主导,概率分布分化, ③ 低温阶段(β→∞):收敛至基态概率分布;g图展示了获得最终问题解的方式,即从所有批量平均场分布中推断解,从中选择能量最低的配置作为最终解。
(一)理论基础:从物理系统到优化问题

图2:组合优化和自旋玻璃问题中复杂的能量景观示意图。如何跨过由能量壁垒所隔绝的能量极小点找到全局能量最低的解,是一个困难的问题。图片来源:Joshua Sortino,Unsplash
从统计物理视角看,组合优化问题在统计物理中被称为自旋玻璃的基态能量问题,变量赋值映射为自旋构型,求解目标函数最小的变量赋值即为求解系统零温下的玻尔兹曼分布。而求解自旋玻璃基态问题的困难之处在于系统的能量景观非常复杂,存在各种由能量壁垒所隔绝的能量极小值。在自旋玻璃理论中,这一现象用副本对称破缺(RSB)理论描述,该理论通过平均场解的不动点来刻画能量景观的崎岖特征。
受RSB理论启发,该研究提出了一种基于变分自由能最小化的通用方法。自由能是批处理(即独立副本)变分平均场分布的函数,通过机器学习中的梯度优化器进行最小化。该方法具有两大特征:
(1)自由能梯度可通过机器学习中的自动微分计算,使其具有通用性并能直接应用于各类COPs;
(2)变分自由能采用深度学习社区开发的成熟优化技术(如Adam)进行最小化。
值得注意的是,所有批处理中的平均场概率都并行更新,从而充分利用GPU的计算能力实现高效执行,大幅加速大规模问题的求解。
(二)方法创新:四步突破
(1)变分近似:平均场分布逼近玻尔兹曼分布
对于组合优化问题,其目标函数E(σ)可映射为物理系统的能量模型,其零温玻尔兹曼分布:
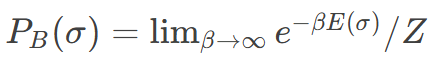
则对应着的基态对应最优解。而计算上述公式属于#P难问题,在统计物理中,变分平均场方法通过假设系统各自由度相互独立来简化复杂概率分布的描述,即用可分解的乘积分布,因此FEM采用如下所示的平均场变分分布来逼近原始的玻尔兹曼分布:
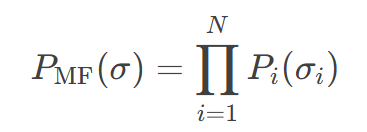
其中Pᵢ(σᵢ)为第i个自旋的边缘概率,通过优化上述两个分布之间的KL距离来实现对问题的求解,而这一目标函数等价于优化以下变分自由能函数:

其中内能公式为:
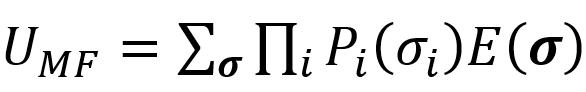
熵的公式为:
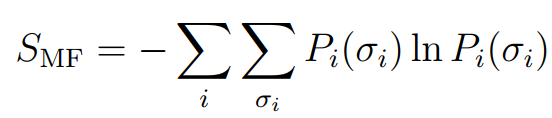
按照上述公式,可以将推导出各个组合优化问题(COPs)对应的自由能函数,从而可以对齐进行可微分求解,该研究工作中推导了以三类典型问题的自由能公式,分别是:
①最大割问题(对应图1中的Ising问题):
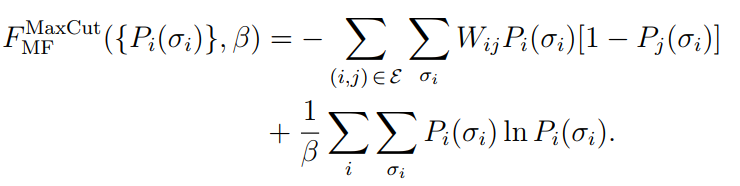
②平衡最小割问题(bMinCut问题,对应图1中的多值问题):
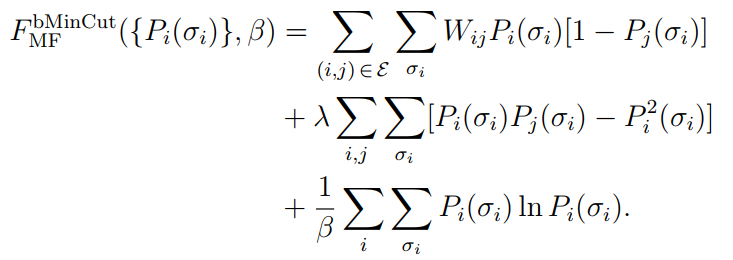
③ 最大可满足性问题(MaxSAT问题,对应图1中的多体交互问题):
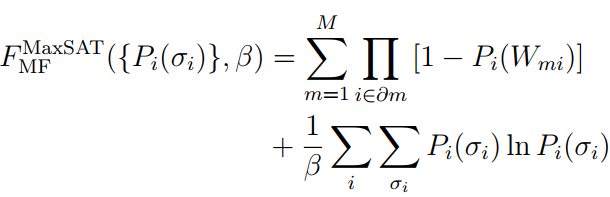
(2)自由能优化:能量-熵平衡的泛函最小化
通过将边缘概率Pᵢ(σᵢ)参数化为局部场的hᵢ(σᵢ)softmax函数:
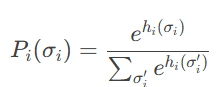
最终上述自由能最小化问题可以转换对自由能关于hᵢ(σᵢ)的泛函最小化问题,其梯度的形式如下所示:
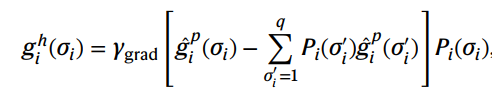
(3)自动微分:基于梯度的反向传播
基于上述问题转换后可以直接通过PyTorch/TensorFlow自动微分技术对各个问题通过反向传播算法进行求解,同时该研究还手工推导了各个问题的梯度的具体形式。
(4)退温策略:温度调制的渐进优化
由于温度对于自由能的计算影响较大,该研究采用常见的两种退温策略进行训练:
①指数退温方式
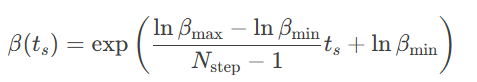
②逆线性退温策略
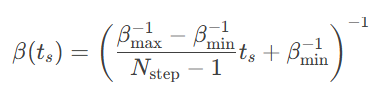
除了上述技巧,该研究还充分考虑问题本身的特性,基于副本方法对所有批处理中的平均场概率都并行更新,从而充分利用GPU的计算能力实现高效执行,大幅加速大规模问题的求解。
三、性能验证:全面超越现有技术
三、性能验证:全面超越现有技术
为了验证FEM算法的效果,该工作重点考虑了三类组合优化问题:
在最大割问题(MaxCut)测试中,FEM在2000节点全连接图K_{2000}上仅用1000次退火步骤即达到已知最优解(33,337),并在G-set基准测试的54个实例中,有33个实例的求解速度超越当前最优算法dSBM:
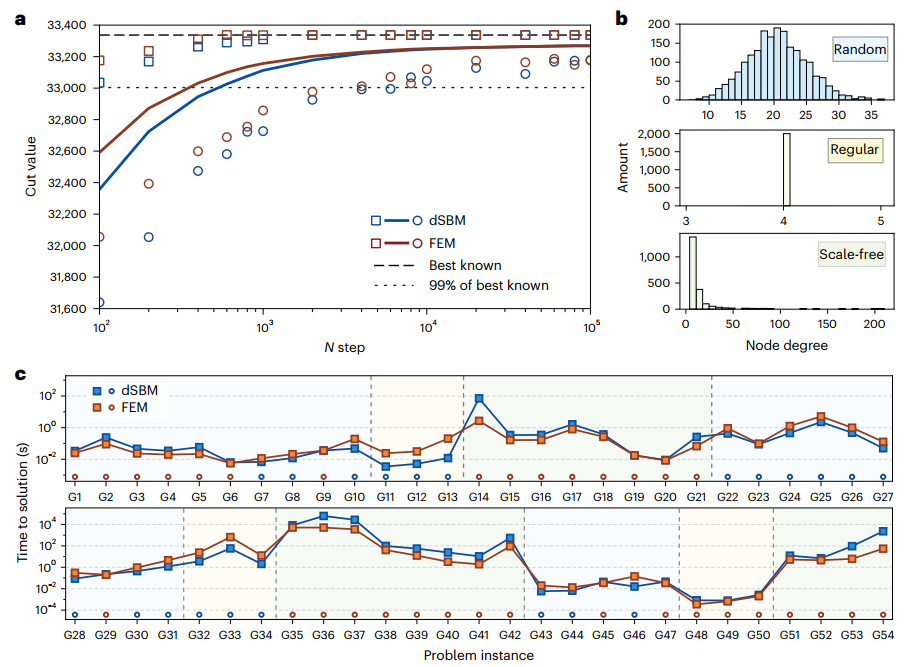
图3:FEM算法在MaxCut问题上的表现
针对平衡最小割问题(bMinCut),FEM在Chris Walshaw存档的真实世界图(如add20、3elt)上全面优于METIS,尤其在32分组时显著超越竞赛优胜算法KaFFPaE:
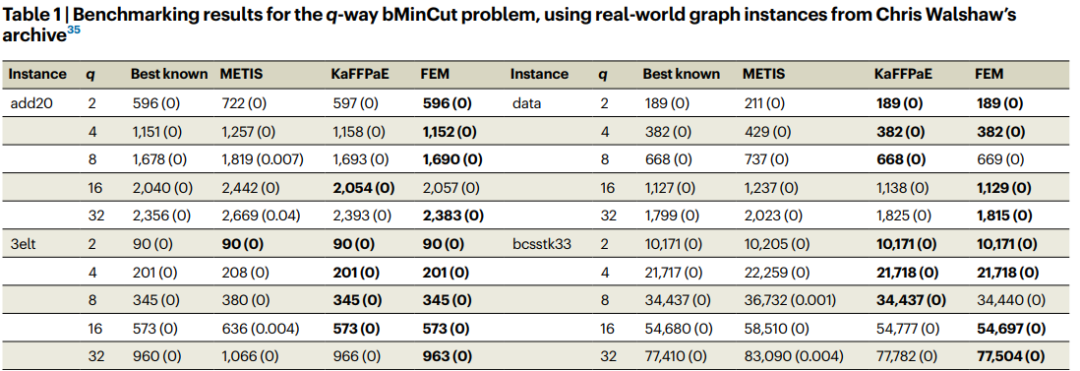
表1:FEM算法在bMinCut问题上的表现
在百万节点随机图在bMinCut问题上的测试中,FEM的归一化割值比METIS低22-26%(图4):
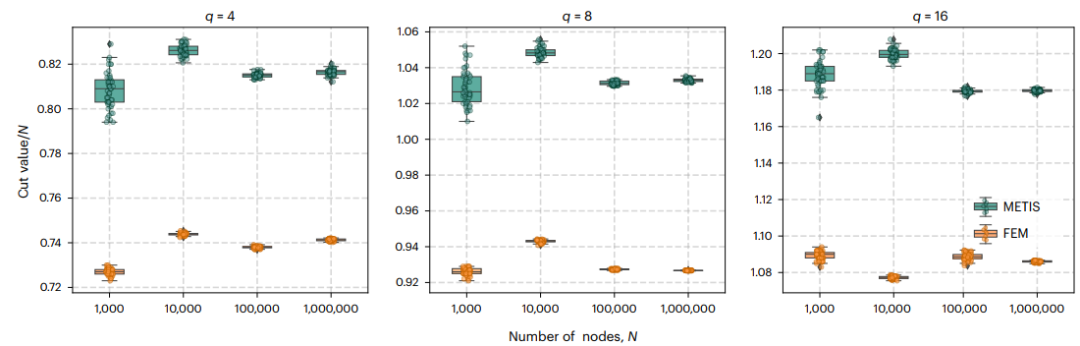
图4:FEM算法在百万规模随机图的bMinCut问题上的表现
同时该研究还在FPGA芯片验证任务进行了实验,结果表明FEM算法可以实现22.5-26.6%的通信量优化(图5)。
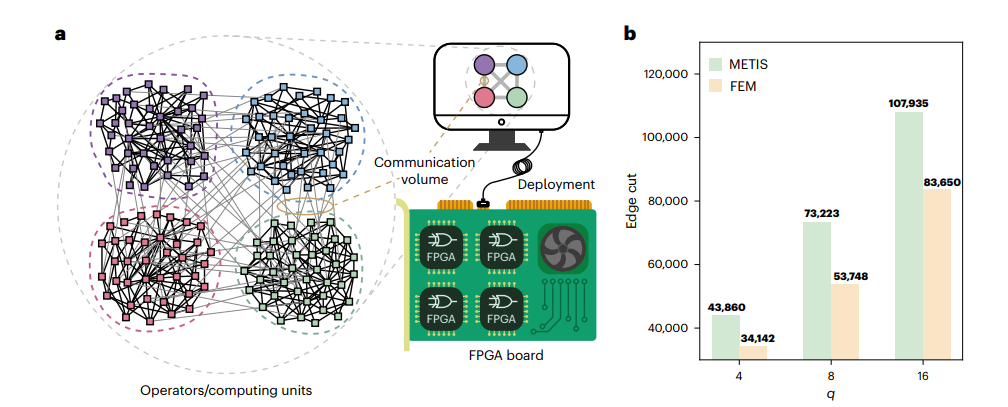
图5:FEM算法在FPGA芯片验证任务上的表现
对于高阶交互的最大可满足性问题(Max k-SAT),FEM在MaxSAT 2016竞赛的454个实例中,对标了SsMonteCarlo, Ramp, borealis, SC2016, CCLS, CnC-LS, Swcca-ms, HS-Greedy和CCEHC等多个求解器,其中FEM在448个问题上找到最优解,其余6个仅差1个子句,全面领先Max-CTDS算法(图6a),且GPU加速显著提升求解效率(图6b)。
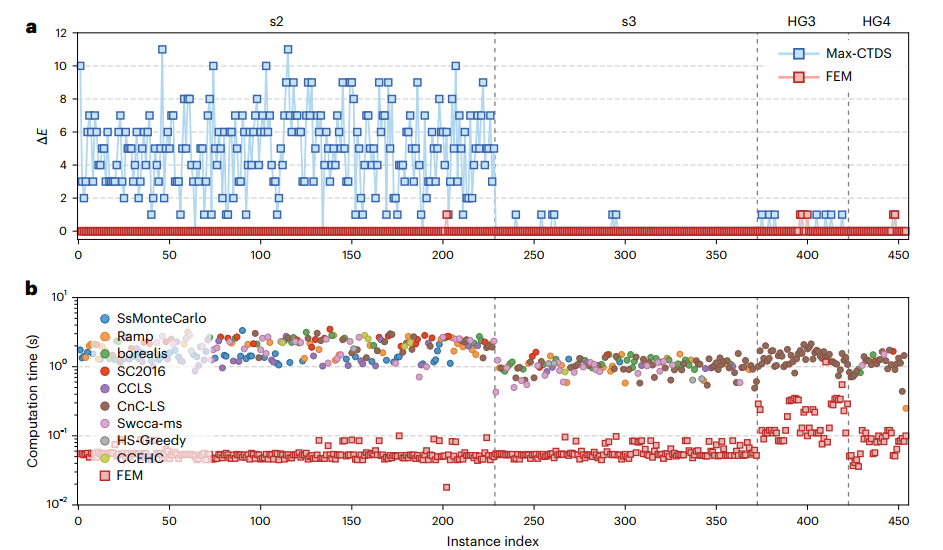
图6:FEM算法在MaxSAT问题上的表现和时间对比
四、学科融合的范式突破:
从物理理论到智能计算的跨越
四、学科融合的范式突破:
从物理理论到智能计算的跨越
该工作提出了自由能机器(FEM)这一通用框架用于求解组合优化问题。大量基准测试证明了该方法的优越性,凸显了统计物理与机器学习融合的巨大潜力。这一创新方法在科学与工业领域具有广泛应用前景。然而,作者认为当前方法仍存在以下改进空间:首先,参数调优依赖人工且受限于现有优化器性能,未来需开发自动化超参数调节机制;其次,虽然FEM在随机图上的平衡最小割问题已显著优于METIS,但简单的平均场假设在副本对称破缺(RSB)场景下可能陷入局部最优,需引入更复杂的分布表示,如基于消息传递的微正则系综方法可能更具理论优势。针对完全RSB问题,现有框架的效能可能受限,但通过改进退火策略和优化器设计有望提升性能。未来我们将探索将更高级的理论(如Thouless-Anderson-Palmer方程、置信传播等)融入FEM框架。这项研究最深刻的启示在于:19世纪提出的自由能概念通过学科交叉在现代计算领域焕发新生,这既印证了基础科学的长期价值,也揭示了学科边界融合催生创新的规律,更表明物理建模思想仍是推动计算变革的重要指引。
参考文献
[1] Shen, ZS., Pan, F., Wang, Y. et al. Free-energy machine for combinatorial optimization. Nat Comput Sci (2025). https://doi.org/10.1038/s43588-025-00782-0
[2] 中国科学院理论物理研究所.Free Energy Machine: 结合统计物理与机器学习的组合优化新方法[EB/OL].https://itp.cas.cn/kxyj/kydt/202503/t20250328_7571836.html, 2025–03–28/2025–04–03.
[3]Huang, Haiping. Statistical mechanics of neural networks. Vol. 310. Singapore: Springer, 2021.

审校

非平衡统计物理读书会启动!
2024年诺贝尔物理学奖授予人工神经网络,这是一场统计物理引发的机器学习革命。统计物理学不仅能解释热学现象,还能帮助我们理解从微观粒子到宏观宇宙的各个层级如何联系起来,复杂现象如何涌现。它通过研究大量粒子的集体行为,成功地将微观世界的随机性与宏观世界的确定性联系起来,为我们理解自然界提供了强大的工具,也为机器学习和人工智能领域的发展提供了重要推动力。
为了深入探索统计物理前沿进展,集智俱乐部联合西湖大学理学院及交叉科学中心讲席教授汤雷翰、纽约州立大学石溪分校化学和物理学系教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学物理系助理教授唐乾元,以及多位国内外知名学者共同发起「非平衡统计物理」读书会。读书会旨在探讨统计物理学的最新理论突破,统计物理在复杂系统和生命科学中的应用,以及与机器学习等前沿领域的交叉研究。读书会从12月12日开始,每周四晚20:00-22:00进行,持续时间预计12周。我们诚挚邀请各位朋友参与讨论交流,一起探索爱因斯坦眼中的普适理论!
详情请见:从热力学、生命到人工智能的统计物理之路:非平衡统计物理读书会启动!
6. 探索者计划 | 集智俱乐部2025内容团队招募(全职&兼职)










