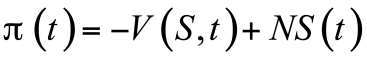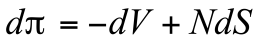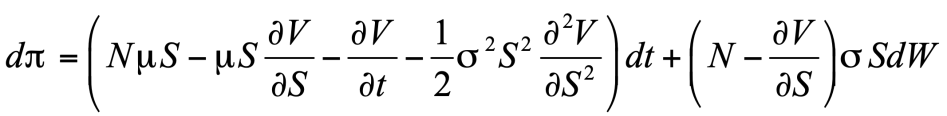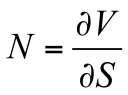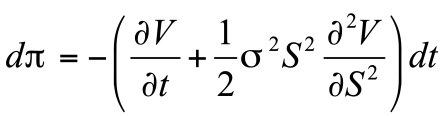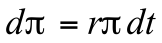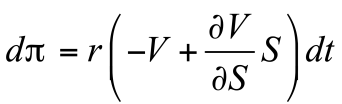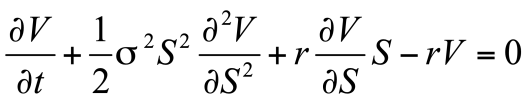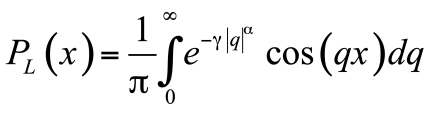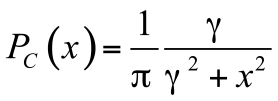列维分布最重要的特点是在大数值时具有幂律尾部。例如,α=1时列维分布的特例是正值x的柯西分布,其公式为
在大数值时会随着x-(α+1)而下降。柯西分布是可归一化的(概率积分为一),其特征尺度由γ设定,但它的均值是发散的,违反了中心极限定理[3]。对于满足中心极限定理的分布,增加分布的样本数可使均值收敛于一个有限值,然而,对于柯西分布来说,增加样本数会增加出现黑天鹅的几率,黑天鹅会使均值偏斜,在样本数无限多的情况下,均值会发散到无穷大。这就是为什么说柯西分布有一个“沉重的尾部”,它包含罕见但振幅较大的离群事件,这些事件会不断移动平均值。
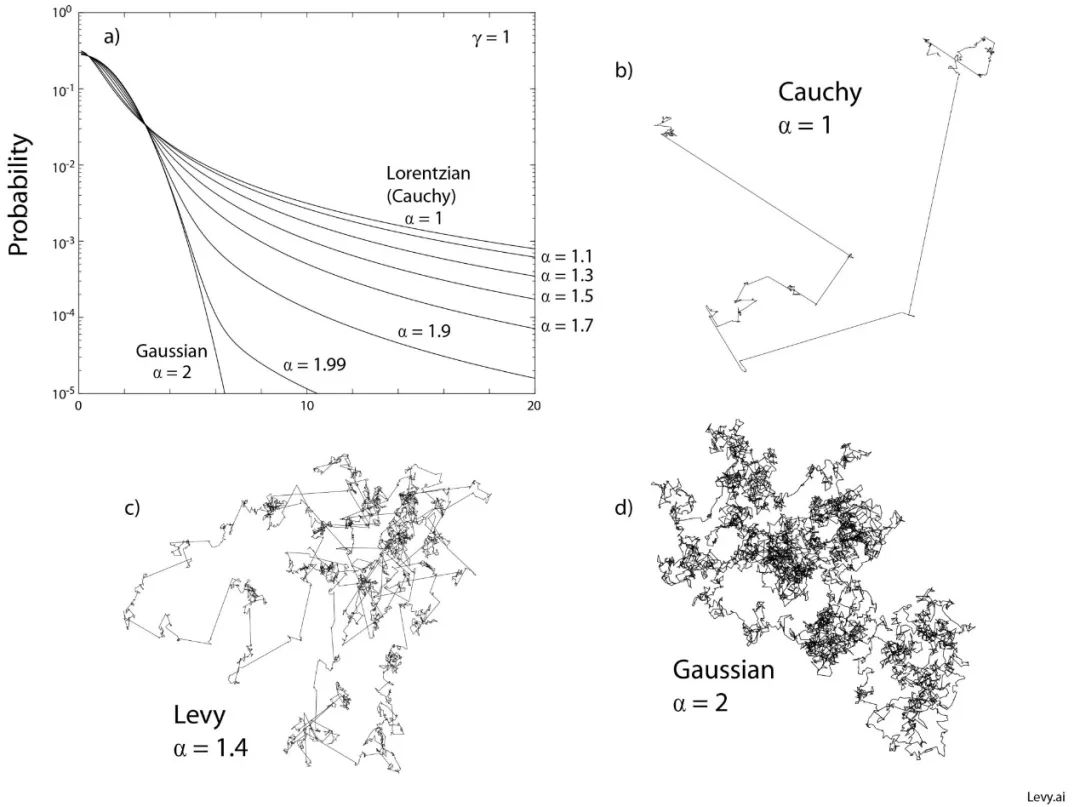
下图显示了在α=1(柯西分布)和α=2(高斯分布)之间的列维稳定概率分布函数示例。即使在非常接近高斯分布的α=1.99的情况下,也可以看到严重的重尾现象。图中显示了α=1、α=1.4和α=2的二维列维随机游走的例子。在高斯分布的情况下,均方位移表现良好且有限,然而,所有其他情况下,均方位移都是发散的,这是因为当α接近1时,路径长度变大的可能性增大。
从α=1(柯西)到α=2(高斯)参数范围内的对称列维分布函数。α<2时的列维飞行具有细菌运动中经常出现的奔跑和翻滚行为。
列维概率分布函数的惊人之处在于,它们在自然现象中十分常见,几乎所有具有尺度不变性(scale invariance)的过程中都会出现严重的列维尾。然而,作为学生,我们几乎对它们视而不见,似乎泊松和高斯统计就是我们需要知道的一切,但无知并不是幸福。正是高斯统计假设导致了 Black-Scholes 模型的失败。
尺度不变过程通常是质量或能量自然级联的结果,因此作为中性现象出现。然而,在一些有偏现象中,列维过程会导致某种形式的优化,生物背景下的列维随机游走就是这种情况。
随机游走是统计物理学的基石之一,也是布朗运动的基础。爱因斯坦利用布朗运动推导出著名的扩散统计力学方程,证明分子物质的存在;让·佩林(Jean Perrin)因其对爱因斯坦理论的实验证明而获得诺贝尔奖;朗之万(Paul Langevin)利用布朗运动将随机微分方程引入统计物理学;而列维则利用布朗运动来说明数学概率论的应用,并写下了他最后一本颇具影响力的著作。
对随机游走的大多数研究都假定步长或速率为高斯或泊松统计,但当步长取自列维分布时,就会出现一种特殊形式的随机游走。这就是列维随机游走,贝努瓦·曼德布洛特(Benoit Mandelbrot)(列维的学生)将其命名为“列维飞行”(Lévy Flight),并对其分形特征进行研究。
列维随机游走最初是作为理想数学模型来研究的,但近年来对其有许多发现,在动物觅食行为中观察到列维随机游走,甚至在细菌的奔跑和翻滚行为中也观察到列维随机游走,据推测,这种觅食策略能让动物对随机分布的食物来源进行最佳采样。有证据表明,分子在细胞内运输中存在列维行走,这可能源于拥挤的细胞内邻域内的随机运动。人们还观察到一种中间状态[4],即细胞内的细胞器和囊泡在沿着细胞骨架附着、迁移和脱离驱动它们的分子马达时,可能具有列维行走的特征。
原文链接:
https://galileo-unbound.blog/2023/02/08/paul-levys-black-swan-the-physics-of-outliers/
Paul Lévy, Calcul des probabilités (Gauthier-Villars, Paris, 1925).
Paul Lévy, Théorie de l’addition des variables aléatoires (Gauthier-Villars, Paris, 1937).
Paul Lévy, Processus stochastique et mouvement brownien (Gauthier-Villars, Paris, 1948).
R. Metzler, J. Klafter, The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Physics Reports-Review Section Of Physics Letters 339, 1-77 (2000).
J. Klafter, I. M. Sokolov, First Steps in Random Walks : From Tools to Applications. (Oxford University Press, 2011).
F. Hoefling, T. Franosch, Anomalous transport in the crowded world of biological cells. Reports on Progress in Physics 76, (2013).
V. Zaburdaev, S. Denisov, J. Klafter, Levy walks. Reviews of Modern Physics 87, 483-530 (2015).
[1] Black, Fischer; Scholes, Myron (1973). “The Pricing of Options and Corporate Liabilities”. Journal of Political Economy. 81 (3): 637–654.
[2] P. Lévy, Théorie de l’addition des variables aléatoire (1937)
[3] The central limit theorem holds if the mean value of a number of N samples converges to a stable value as the number of samples increases to infinity.
[4] H. Choi, K. Jeong, J. Zuponcic, E. Ximenes, J. Turek, M. Ladisch, D. D. Nolte, Phase-Sensitive Intracellular Doppler Fluctuation Spectroscopy. Physical Review Applied 15, 024043 (2021).
经济学理论的发展与社会环境变化密切相关。一方面,伴随计算机的发展,相应的研究技术日渐成熟,例如非线性动力学、复杂网络、ABM等,为研究者提供了更强大的分析工具;另一个方面,对“均衡”的经济学的研究,不能够解释实际的经济现象,例如金融危机、创新产生的新的发展模式等,研究者开始重视经济学的“非均衡”现象,把经济系统看做复杂系统,并力图做出更能反映现实的研究。经济学内慢慢出现了一种基于更加现实的假设的研究进路,复杂经济学一个新的经济学框架正在形成。为了促进此领域的交流与合作,我们发起了复杂经济学读书会。
复杂经济学读书会第二季由北京师范大学李红刚、王有贵、张江、陈清华老师以及中山大学袁先智老师联合发起,围绕复杂经济学的内涵、基本方法、普适规律、应用场景四个方面进行探讨,并计划组织三次圆桌讨论,与国内外学者进行深入探讨。热诚欢迎对复杂系统研究和经济学感兴趣的学生和学者加入这个读书会,一起探索和探讨经济复杂系统的真谛!