关键词:脑网络,神经网络活动,混沌系统,非线性动力学,动力学平均场论
Dimension of Activity in Random Neural Networks
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.118401
神经网络是高维非线性动力系统,通过许多连接单元的协调活动来处理信息。要理解生物和机器学习网络如何行使功能和学习,需要了解这种协调活动的结构,例如单元之间的交叉协方差中所包含的信息。
自洽动力学平均场论(Self-consistent dynamical mean field theory,DMFT)已经阐明了随机神经网络的一些特征,特别是它们可以产生混沌活动,然而,使用这种方法计算交叉协方差尚未实现。
这项研究通过双位点空腔动力学平均场论(two-site cavity DMFT)方法自洽地计算交叉协方差。研究者利用这个理论来探讨一个具有独立同分布(i.i.d.)耦合的经典随机网络模型中的活动协调的时空特征。该方法适用于广泛的单个单元动力学,并可推广到非独立同分布耦合。作为后者的一个示例,研究中分析了部分对称耦合的情况。
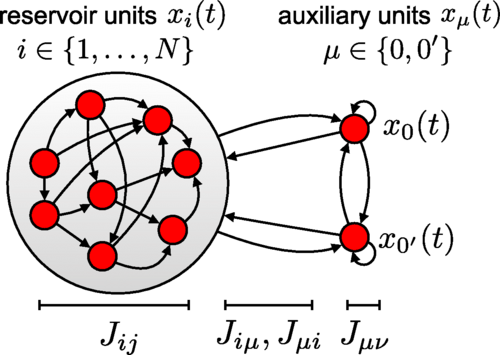
图1. 双位点空腔动力学平均场论(two-site cavity DMFT)概览。两个辅助单元(auxiliary units)的位点(称为空腔单元)创造了一个空腔,与此同时,网络的其余部分(储备池,reservoir)产生混沌活动。然后引入空腔单元,它们会对储备池产生扰动。空腔单元的动力学方程产生一对扰动耦合平均场方程,表示一对单元。注意到空腔对在统计上等价于任何储备池对,可以构造自洽条件。
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「我的集智」推送论文信息。扫描下方二维码即可一键订阅:

推荐阅读