PRL速递：麦克斯韦妖进入华尔街：随机热力学遇见预期效用理论

关键词：随机热力学，信息论，预期效用理论

论文题目：

Maxwell’s Demon Walks into Wall Street: Stochastic Thermodynamics Meets Expected Utility Theory

论文地址：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.197103

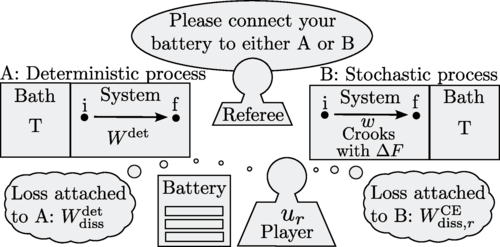
在标准热力学的自上而下方法中，第二定律规定自然界固有的不可逆性。相比之下，在统计力学的自下而上方法中，动力学是可逆的。随机热力学（tochastic thermodynamics）在这两种方法之间建立了一种联系：虽然短暂违反第二定律是允许的，但平均而言，该定律仍然成立。

热力学与信息论之间的相互作用有着悠久的历史，但其定量表现仍在不断探索中。这项研究将经济学中的预期效用理论（expected utility theory）引入随机热力学中。研究证明，在遵循 Crooks 涨落关系的过程中，对于风险厌恶为 r=α−1 的玩家，正向过程与其逆过程之间的每个 α Rényi 散度都具有与耗散功（或更广泛地说，熵产生）“确定等价”的操作意义。已知的两种情况被重新解释，其中 α=1 与风险中性玩家相关联，α=∞ 与极端风险厌恶玩家相关联。在新结果中，α=0 这一条件描述了一个风险追求型玩家的行为，愿意押注于短暂违反热力学第二定律的事件。该方法还导致了广义的Jarzynski 等式，并可推广到更广泛的统计散度类。

图. 功耗散游戏的示意图。用CARA效用函数模拟的玩家面临的选择。玩家需要使用其电池来执行以下两种过程之一：(A) 确定性过程：将需要固定量的工作；(B) 随机过程：在这个过程中，工作遵循 Crooks 涨落关系，其自由能差为ΔF。风险厌恶型玩家（r > 0）会选择确定性过程，除非 W^det 太大；风险追求型玩家（r < 0）会选择随机过程，除非W^det 足够低。“确定等价”决定了玩家在随机过程和确定性过程之间切换的数值。

编译｜梁金

复杂经济学读书会第二季