1970年,数学家约翰·康威(John Conway)发明了一个著名的”游戏,名为“生命游戏”(Conway’s Game of Life)。
生命游戏模拟的是自然界的生命演化,它在一个简单的世界中,设置了一个细胞自动机。这个世界是由一个无限的正方形网格细胞平面构成的,细胞可以有两种状态:“生”或“死”。它们会在离散的时间里迭代演化。
1、如果一个死亡细胞周围有3个(等于3)活的相邻细胞,那么在下一个时间步骤里,这个细胞就会变成活细胞;
2、如果一个活细胞周围只有0个或1个(小于2)活的相邻细胞,那么在下一个时间步骤里,它就会因为“孤独”而死;
3、如果一个活细胞周围有4个或4个以上(大于3)活的相邻细胞,那么在下一个时间步骤里,它就会因“拥挤”而死;
4、如果一个活细胞周围有2个或3个活的相邻细胞,那么在下一个时间步骤里,它仍然可以存活。
这几条简单的规则产生了复杂的行为,它显示了生命游戏中的细胞可以从一个简单的初始状态,随时间演化出高度复杂的特征。
在这个模拟生命演化的游戏中,一些细胞组成的图样可以在经历有限的时间步骤后回到它们的初始状态。这种图样通常按其周期进行分类的,即图样在出现重复状态之前所经历的步骤数。
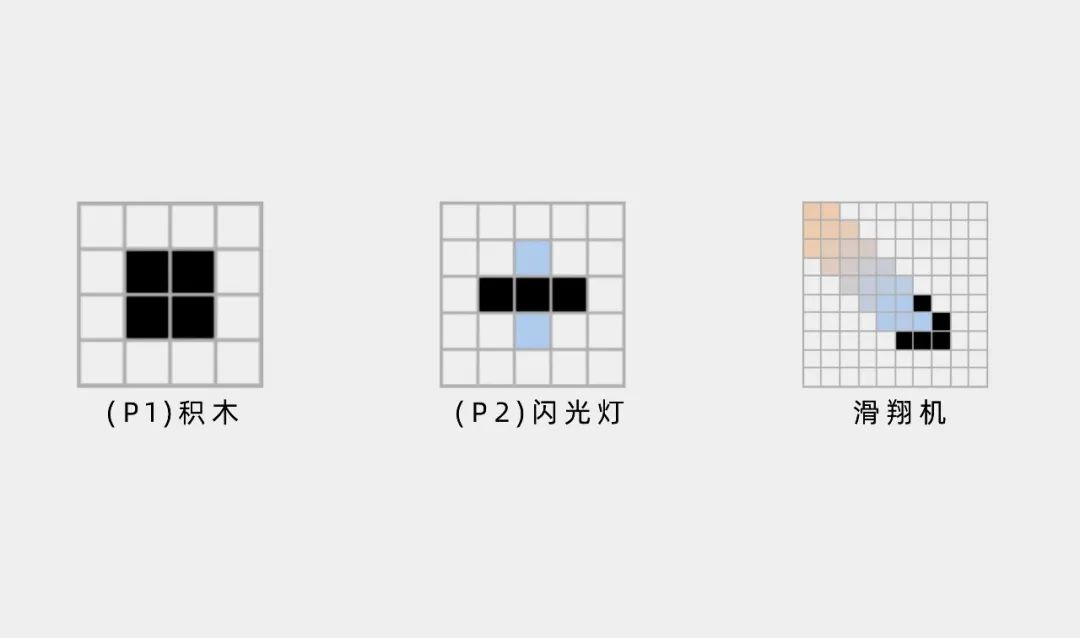
比如,一个2×2的活细胞组合(也被称为“积木”),就是一个周期为1的图样例子,这种图样也被称为静物。有些图样具有2个或更多的周期,这些图样被称为振荡器,比如一个1×3的活细胞组合(也被称为“闪光灯”)。还有一些图样可以复现它们的初始状态,但会在网格平面上发生平移,这种图样被称为太空船,比如下图中最右边的被称为“滑翔机”的图样的周期为4,但它在经过4次迭代后,会沿着对角线移动一格。
一个网格所代表的细胞周围有8个相邻的网格,通常用黑和白两种颜色来分别代表网格上的细胞的生和死。(图/Brown et al. via arxiv.org)
事实上,没有人确切知道生命游戏的极限在哪里,计算机科学家仍在努力解决许多与之有关的未解难题,其中一个问题就与周期有关:在生命游戏中,是否对于所有周期,都存在对应的振荡器?换句话说,生命游戏是全周期的吗?
上世纪90年代中,数学家David Buckingham设计了一种技术,可以创建周期大于61(p≥61)的振荡器。在千禧年之交,只剩下12个周期仍需寻找,它们是19、23、27、31、34、37、38、39、41、43、51、53。事实证明,缺失的“中间周期”(15 < p < 43)的振荡器更加难以寻找,尤其是那些素数周期。
不过,在过去的一二十年里,随着计算机速度的提高和更优的搜索技术的出现,这些缺失的周期开始被慢慢填补,只剩下最后两个:19和41。
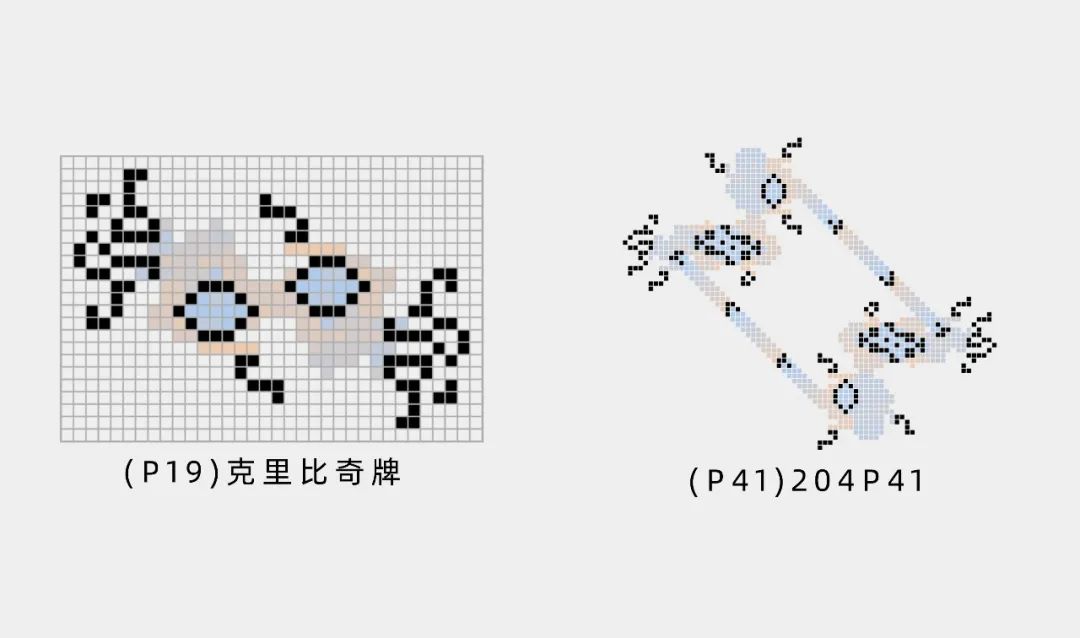
12月5日,一组“生命游戏”爱好者在论文预印网站arXiv上提交了一篇新的论文,表明他们已经发现了最后两个周期的振荡器,证明了:生命游戏是全周期的。
新研究称找到了生命游戏中,周期为19和41的振荡器。(图/Brown et al. via arxiv.org)
研究人员表示,虽然这一成果目前没有任何实际应用,但它满足了痴迷于生命游戏的所有爱好者的好奇心,并且这项工作展示了一些非常富有创意的技术。
现在问题解决了,那么下一步该做什么呢?研究人员指出,还存在许多尚未解决的问题,比如太空船的速度问题,以及为给定周期找到最小的振荡器等。还有很多有趣的问题,正如研究人员所说的:“生命游戏的工作永远不会有完成的一天!”
https://arxiv.org/abs/2312.02799
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「我的集智」推送论文信息。扫描下方二维码即可一键订阅: