Theoretical foundations of studying criticality in the brain
https://direct.mit.edu/netn/article/6/4/1148/112392/Theoretical-foundations-of-studying-criticality-in
1. 为什么研究大脑临界性的理论基础
2. 大脑临界性的基本分类
3. 神经元雪崩和大脑临界性
4. 大脑临界性的平均场和随机场论
5. 神经雪崩指数和统计技术
6. 总结
在过去几十年中,作为大脑中高效转换大脑皮层状态[1]、神经响应动态范围的最大化[2]、信息传输和表征的优化[2-4]等性质的可能解释,临界大脑假说得到了越来越多的关注。到目前为止,大脑临界状态的普适特性,如发散的相干长度、具有幂律行为的神经雪崩活动和微观尺度上的长程相关性,已经在数学模型和实验数据中得到广泛的观察[5-9]。
尽管如此,大脑临界性的理论基础研究最初被认为是不可理解的并且与神经科学无关。但实践表明,忽略这些物理和数学背景并不能显着提高大脑临界性研究的可及性。相反,缺乏对理论基础的详细解释经常误导神经科学家,导致人们对大脑临界性的精确含义、识别标准和生物学推论产生各种困惑。
为了解决这个问题,清华大学心理学系&脑与智能实验室、交叉信息研究院、钱学森力学班、法国巴黎城市大学数学科学中心、中科院自动化研究所的研究团队使用神经科学的术语提出了一个独立的大脑临界性框架,回顾并重新表述了(1)分析推导大脑临界性的物理理论和(2)根据经验数据计算估计大脑临界性的统计技术。鉴于对神经雪崩的频繁误解,作者的讨论主要集中在大脑微观尺度上的大脑临界性分析。指导该综述的目标有三部分:
1. 解释为什么临界性对大脑很重要
2.了解什么是大脑临界性以及它传达的有关大脑的信息
3. 确认如何识别潜在的大脑临界性并确保分析的有效性
大脑临界性经常让神经科学家感到困惑,因为有太多不同的现象以这个名称进行研究,而没有被正确分类。在本文中,大脑临界性指神经动力学中的一类临界性过程,其中不稳定的波动似乎会降低动态稳定性。为了提出一个系统的分类框架,我们讨论了与大脑临界性相关的三个研究维度。表1提供了所有必要的概念以便理解。
|
|
|
|
|
系统在同时最大化熵的保守能量的情况。处于平衡状态的系统状态的稳定概率分布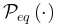 是玻尔兹曼分布。平衡态下,系统状态和之间的转换满足细致平衡条件 是玻尔兹曼分布。平衡态下,系统状态和之间的转换满足细致平衡条件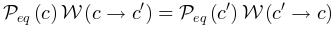 ,其中 ,其中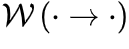 表示转移概率。 表示转移概率。
|
|
|
由于系统状态之间的转换打破了细致平衡条件而导致系统失衡的情况。换句话说,状态之间的转换变为方向性而非对称性。
|
|
|
一个系统没有被任何外部机制调整下内部复杂性增加的过程。所有潜在的涌现属性都是由系统内部的内生反馈过程或其他内部因素创建的。
|
|
|
系统通常接近于分隔多个系统状态之间的特定临界点。微小的扰动足以使系统在状态之间经历急剧的转变。
|
|
|
临界所需的所有统计物理关系都被系统遵守,但特征变量的实际值与完美临界性存在轻微且不稳定的偏差。这些偏差存在且通常与数据噪声无关。
|
非平衡态 首先,与其他生物系统类似,大脑通常表现出远离平衡状态的时间演化[10,11]。这些偏离平衡的现象是由于多种内生原因而产生的[10,12],打破了支持意识、感知和适应的细致平衡[11,12]。因此,至少在大多数神经动力学模型和经验数据集中,神经动力学潜在的临界现象基本上是非平衡的,不能用平衡统计力学来表征。在图1A中,我们说明了平衡动力学和非平衡动力学之间的差异。
微调与自组织 其次,大脑临界性存在两种机制解释。一种机制是源于外部对大脑的操控[13,14],或自上而下的生物学过程从大脑全局影响神经动力学[1]。通过这些外生机制,神经动力学被动地微调(fine-tuning)来靠近或远离普通临界性(OC, ordinary criticality)。另一种机制包括所有神经动力学的内源性因素[15]。这些机制在神经动力学上局部作用,形成反馈控制环来支持神经动力学向临界点的自组织行为。这种自发出现的大脑临界性被推测为一种自组织临界性(SOC, self-organized criticality)[16]。在图1B中,我们展示了大脑中普通临界性和准临界性的概念图示。
图1 大脑临界性的概念图。(A)平衡和非平衡动力学之间的差异。大脑状态由三个系统组成部分来表征。我们举例说明了这些状态之间的非平衡动力学实例。(B)外源机制的微调使大脑从非临界状态(左上)进化到临界状态(右上)。内源性机制使大脑能够自组织从非临界状态(左下)到临界状态(右下)。(C)增加刺激强度会扩大准临界系统中完美临界点周围的准临界区域。(D)自组织准临界系统逼近临界点的过程由两个阶段组成。在第一阶段,大脑基于某些内源机制从非临界状态自组织到准临界区域。在第二阶段,需要额外的外源机制将大脑微调到临界点。否则,大脑只会在准临界区内徘徊。(E)从敏感性角度看四种大脑临界性的差异。对于标准的大脑临界性(例如,普通临界性和自组织临界性),敏感性在临界点变得发散(即无限)。对于非标准的大脑临界性(例如,准临界性和自组织准临界性),敏感性始终是非发散的(即有限的)。准临界区定义为敏感性值不小于特定阈值(例如半最大值)的所有控制参数的集合。(F)四种大脑临界性的共性和差异。
标准临界与准临界 第三,由于刺激驱动或内源性因素,大脑临界状态经常以非标准形式发生。在特征变量的实际值上可以看到与完美大脑临界性的轻微且不稳定的偏差,同时这些实际特征变量依然在标准临界性所需的统计物理关系附近,因此准临界性与非临界性区分开来[7]。
对于普通临界性(OC),其非标准形式被称为准临界性(qC,Quasi-criticality)[7,17]。多种机制可以迫使大脑偏离OC并表现出qC神经动力学,其中刺激导致的准临界可能是最常见的一种。一般来说,足够强的刺激驱动可以捕获甚至控制神经动力学。与外部输入抑制不规则神经动力学的情况类似,太强的刺激可能会引起强烈但不易变化的神经动力学,使大脑偏离完美的临界点。由刺激强度ν、不应期长度τ、分支比κ描述大脑在Widom线附近的qC就是一个很好的例子,在Widom线上神经元动力学的敏感性最大化,靠近Widom线表明大脑中存在qC,同时与Widom线的显着偏差表明非临界性[7,17]。在图1C中,我们从概念上说明了刺激如何在大脑中暗示qC。在图2D中,详细展示了Widom线上的qC。
关于SOC,它的非标准形式是根据统计物理学标准定义的。完美的SOC只存在于保守的神经动力学中,其中系统能量(即神经活动)要么在系统内保持不变,只在系统边界上消散,要么在系统内部消散(即体积耗散),其耗散率在系统尺寸极限下逐渐消失[18]。在神经动力学不是保守的更一般情况下,任何体积耗散率都可以破坏完美的SOC[19]。更强的体积耗散意味着更大的偏离完美的SOC。因此,与标准SOC不同,非保守的神经动力学的自组织过程只能使大脑徘徊在临界点附近。任何进一步接近临界点都需要通过额外的外源机制对秩序参数进行精细调整。这个非保守的自组织过程被称为自组织准临界性(SOqC,Self-organized quasi-criticality)[20]。与保守动力学中的SOC类似,神经可塑性[21]、Hebbian规则[22]、短期突触抑制和与尖峰相关阈值增加[23]或与网络拓扑相关的抑制性可塑性[24]可以作为SOqC的潜在自组织机制。由于在实证数据中纯粹的保守型神经动力学相对较少[15,19],我们认为SOqC在大脑中比SOC更为常见。在图1D中,我们提供了一个概念性的例子,描述了大脑在SOqC的作用下向临界点接近的两个阶段。
大脑临界性的分类 上述讨论已经给出了大脑临界性的分类框架,即普通临界性(OC)、准临界性(qC)、自组织临界性(SOC)和自组织准临界性(SOqC)。在图1E中,我们从敏感性的角度比较了这四种类型的大脑临界性。一般来说,在标准临界性的大脑(例如OC和SOC)中,敏感性在临界点发散,而在非标准临界性的大脑(例如 qC 和 SOqC)的准临界性区域中,敏感性不会发散。在图1F中,我们总结了我们评述中讨论的这四种大脑临界性之间的共性和差异。
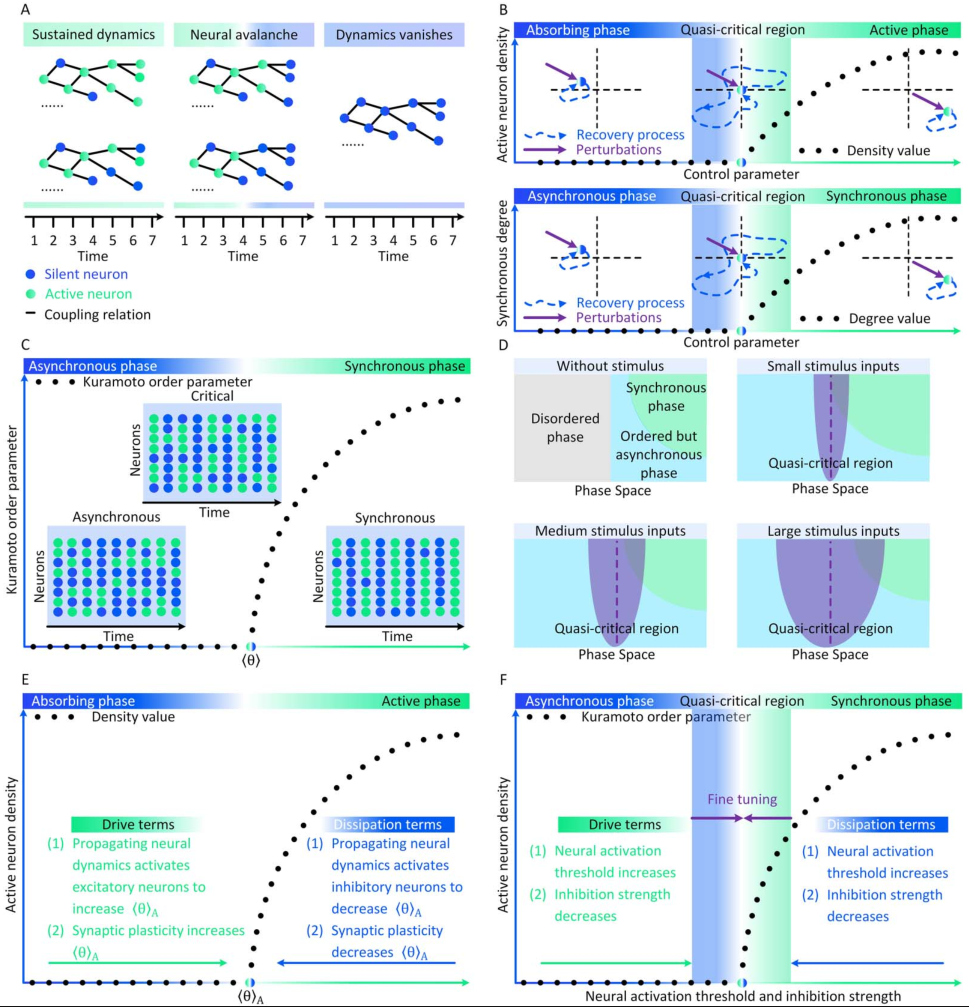
图2 神经雪崩和大脑临界性之间关系的概念图。(A)神经雪崩、自我维持的神经动力学和消失的神经动力学实例。(B)吸收相和活跃相空间、同步相和异步相空间相同扰动后脑状态的恢复过程。当大脑远离临界点或准临界区时,扰动后的恢复过程相对较快;当大脑接近临界点或准临界区时,这些恢复过程减慢。(C)大脑状态异步、同步或处于普通临界性时神经动力学的概念图。(D)在没有刺激的情况下,大脑相空间中最初存在无序(灰色)、有序但异步(浅蓝色)、同步(绿色)相。刺激输入意味着大脑的准临界性。刺激强度的增加会扩大Widom线(紫色虚线)周围的准临界区域(紫色)。(E)保守神经动力学中的内源机制如何作为驱动或耗散项发挥作用,以在大脑的吸收相和活跃相之间创建自组织临界性的概念说明。(F)在自组织准临界大脑中,非保守神经动力学中的内生机制仅支持自组织朝向异步和同步相之间的准临界区域。需要额外的外源机制来将大脑微调到临界点。
为了识别大脑中潜在的临界点,研究人员实际上将神经动力学描述为具有吸收状态和雪崩行为的物理系统。一般来说,需要考虑神经动力学的传播,其中神经元要么被激活(“开启”状态),要么保持沉默(“关闭”状态)。沉默神经元可以按照由激活的突触前神经元的数量和神经元之间的耦合强度θ定义的概率被激活。激活的神经元会以恒定的速率自发地变得沉默。这些定义自然支持区分神经动力学的不同相。在这里,我们回顾了神经科学中常见的两种相变过程。
吸收相和活跃相(absorbing vs. active)。吸收相是指神经元之间的耦合较弱并且所有神经元最终变得沉默的情况[25]。一旦神经动力学过程消失,它就无法自行重新出现。大脑需要新的驱动来触发新的神经动力学。另一方面,活跃相对应于“开启”状态在具有强耦合的神经元之间传播的情况,从而导致稳定的自我维持神经动力学(例如,大脑中活跃神经元的非零时间和整体平均密度)。在图2A中,我们展示了神经雪崩、自我维持的神经动力学和消失的神经动力学的概念实例。将ρ(t)表示为t时刻活跃神经元的密度,我们可以简单地将0时刻活跃神经元触发的神经动力学过程的吸收和活跃相表示为
同步相和异步相(synchronous vs. asynchronous)。顾名思义,这两个相分别对应于神经活动中同步出现或消失的情况[26]。同步是指“开启”状态以振荡(尽管不是严格周期性)方式出现的情况。为了量化其潜在存在,我们可以使用变异系数(CV)[26]或Kuramoto序参量[27]来测量神经动力学的变异性。CV可以从不同的角度定义,但最常见的定义是标准差与峰间间隔长度平均值之间的比率。CV值越高意味着同步性越差。对于大多数神经动力学数据,区分同步和异步相的CV阈值的经验选择可能是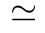 1或
1或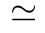 3/2[1]。Kuramoto序参量ω∈[0, 1]基于Kuramoto振荡器模型测量神经动力学的相干程度。当ω=1时,完美同步出现;当ω=0时,完美同步消失[27]。
上述两组相的边界就是临界点,此时大脑处于表现出自我维持(对于吸收和活跃相)或同步(对于同步和异步相)神经动力学的边缘。对吸收或异步相的扰动(例如,神经元之间“开启”状态的传播)没有特征寿命和大小。这些扰动(称为神经雪崩)预计在其生命周期中表现出幂律特性(完全沉默时期之间神经元第一次和最后一次激活之间的时间差)和大小(活动神经元的数量以及偏移)分布。一般来说,神经雪崩的出现意味着神经动力学的减慢,即波动从快(指数)到慢(幂律)变化后大脑状态向基线状态恢复的过程。神经动力学的动态稳定性受到缓慢恢复的限制,因此不能稳健地抵消扰动。因此,在微观尺度上引发的小扰动仍然可能使大脑在宏观尺度上发生急剧变化[28]。在图2B中,我们概念性地说明了当大脑接近临界点或准临界区域时恢复过程如何减慢。
神经雪崩和大脑临界性之间的关系经常被忽视或误解。单独的神经雪崩数据不足以确定大脑临界性的具体类型(即 OC、qC、SOC 和 SOqC),除非提供有关神经雪崩出现机制的附加信息(例如,如果神经动力学是守恒的或自组织)。为了探索具体类型的大脑临界性,研究人员需要根据不同的控制参数明确地给出其定义和序参量。没有严格定义控制和序参量的大脑临界假设是没有信息的[28]。为了呈现概念实例,我们在图2中说明了四种可能的临界现象,每种现象对应于一种具体的大脑临界类型。
3/2[1]。Kuramoto序参量ω∈[0, 1]基于Kuramoto振荡器模型测量神经动力学的相干程度。当ω=1时,完美同步出现;当ω=0时,完美同步消失[27]。
上述两组相的边界就是临界点,此时大脑处于表现出自我维持(对于吸收和活跃相)或同步(对于同步和异步相)神经动力学的边缘。对吸收或异步相的扰动(例如,神经元之间“开启”状态的传播)没有特征寿命和大小。这些扰动(称为神经雪崩)预计在其生命周期中表现出幂律特性(完全沉默时期之间神经元第一次和最后一次激活之间的时间差)和大小(活动神经元的数量以及偏移)分布。一般来说,神经雪崩的出现意味着神经动力学的减慢,即波动从快(指数)到慢(幂律)变化后大脑状态向基线状态恢复的过程。神经动力学的动态稳定性受到缓慢恢复的限制,因此不能稳健地抵消扰动。因此,在微观尺度上引发的小扰动仍然可能使大脑在宏观尺度上发生急剧变化[28]。在图2B中,我们概念性地说明了当大脑接近临界点或准临界区域时恢复过程如何减慢。
神经雪崩和大脑临界性之间的关系经常被忽视或误解。单独的神经雪崩数据不足以确定大脑临界性的具体类型(即 OC、qC、SOC 和 SOqC),除非提供有关神经雪崩出现机制的附加信息(例如,如果神经动力学是守恒的或自组织)。为了探索具体类型的大脑临界性,研究人员需要根据不同的控制参数明确地给出其定义和序参量。没有严格定义控制和序参量的大脑临界假设是没有信息的[28]。为了呈现概念实例,我们在图2中说明了四种可能的临界现象,每种现象对应于一种具体的大脑临界类型。
神经科学家在研究不同临界性时面临的主要挑战之一是如何理解它们的理论关系[29]。克服这一挑战对于理解为什么我们可以使用理论工具验证不同类型的大脑临界性的存在至关重要。为了进行简洁和全面的回顾,我们首先关注吸收相和活跃相之间的大脑临界性。我们概括了[20,30]中的想法以提出一个可能的框架。
OC的Langevin方程 一般来说,吸收相和活跃相空间中的大脑临界性与定向渗透有关[6],这是一种连续相变到吸收态的普适类(普适类指具有相同标度属性的所有系统的集合)[31]。定向渗流理论最初涵盖了OC现象。我们从经典Reggeon场论的变体开始,这是吸收相变的最简单描述[32]。活动神经元场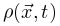 的Langevin方程可以被定义为:
其中
的Langevin方程可以被定义为:
其中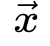 表示空间坐标,
表示空间坐标,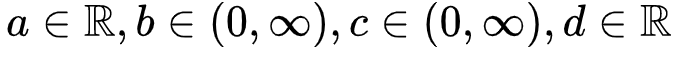 是扩散因子,
是扩散因子,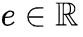 是噪声因子,
是噪声因子,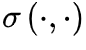 函数是时空域的噪声项。一般来说,
函数是时空域的噪声项。一般来说,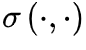 反映了神经元活动的集体扰动,这些扰动在吸收相会消失为零。
反映了神经元活动的集体扰动,这些扰动在吸收相会消失为零。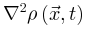 项反映了神经动力学的传播,
项反映了神经动力学的传播,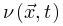 函数定义了根据
函数定义了根据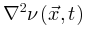 传播的能量(如膜电位),这个函数随着外部驱动
传播的能量(如膜电位),这个函数随着外部驱动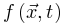 增加,随着体耗散
增加,随着体耗散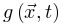 减小。这里我们要求神经元密度和能量始终非负
减小。这里我们要求神经元密度和能量始终非负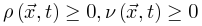 。
很显然,
。
很显然,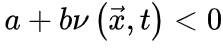 使得神经动力学最终消失(对应吸收相),而
使得神经动力学最终消失(对应吸收相),而 则相反(对应活跃相)。因此,我们可以微调控制参数
则相反(对应活跃相)。因此,我们可以微调控制参数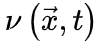 使大脑在
使大脑在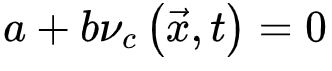 (由νc定义的临界点)处OC。微调依赖于外部机制操纵的
(由νc定义的临界点)处OC。微调依赖于外部机制操纵的 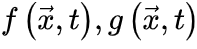 。
qC的Langevin方程 为了导出吸收相和活跃相的qC,我们考虑上述公式(3,4)的平均场近似,
。
qC的Langevin方程 为了导出吸收相和活跃相的qC,我们考虑上述公式(3,4)的平均场近似,
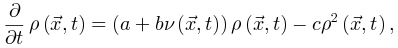 (5)
(5)
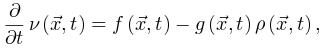 (6)
基于平均场假设,
(6)
基于平均场假设,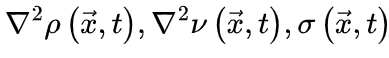 会被忽略。当没有刺激输入。即
会被忽略。当没有刺激输入。即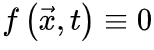 时,活跃和吸收相的临界点是。公式(5,6)的稳定解为
时,活跃和吸收相的临界点是。公式(5,6)的稳定解为
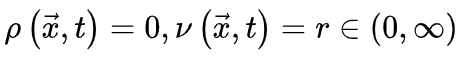
当刺激输入变强,上述稳定解不存在除非满足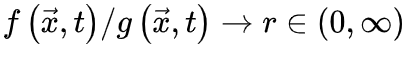 ,此时我们可以导出
此时,临界点
,此时我们可以导出
此时,临界点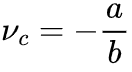 不一定是稳态。除非存在某些理想的外生机制,每当
不一定是稳态。除非存在某些理想的外生机制,每当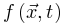 增加时,
增加时,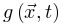 持续增大,否则神经动力学的微调无法消除
持续增大,否则神经动力学的微调无法消除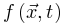 的影响。因此,微调过程可能只能使大脑到达神经动力学敏感性相对较大的准临界区域。最初的OC消失并被qC取代。
SOC的Langevin方程 为了更准确地理解SOC和OC之间的联系,我们可以考虑
的影响。因此,微调过程可能只能使大脑到达神经动力学敏感性相对较大的准临界区域。最初的OC消失并被qC取代。
SOC的Langevin方程 为了更准确地理解SOC和OC之间的联系,我们可以考虑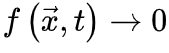 使得
使得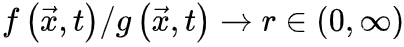 (即时间尺度的无限分离)。因此公式(5,6)的稳态解变为
自组织特性通过以下的过程反映出来:当大脑由于神经动力学消失处于吸收态,即
(即时间尺度的无限分离)。因此公式(5,6)的稳态解变为
自组织特性通过以下的过程反映出来:当大脑由于神经动力学消失处于吸收态,即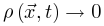 ,此时公式6变为
,此时公式6变为 使得大脑转向活跃相;当大脑处于活跃相,由于
使得大脑转向活跃相;当大脑处于活跃相,由于 公式6变为
公式6变为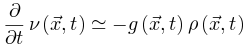 来降低神经动力学。因此这些反馈控制回路将驱使大脑到达临界点。
SOqC的Langevin方程 对于SOqC,非零体耗散打破了守恒定律,在神经动力学中产生了非马尔科夫分量[20,30]。在理想情况下,足够大的神经动力学驱动项(如刺激输入)以任意慢的时间尺度发生(即仅发生在神经雪崩之间的间隔内),大脑表现出纯粹的动态渗透行为[30]。为了理解这个属性,让我们考虑公式5和6的变体,其中耗散项
来降低神经动力学。因此这些反馈控制回路将驱使大脑到达临界点。
SOqC的Langevin方程 对于SOqC,非零体耗散打破了守恒定律,在神经动力学中产生了非马尔科夫分量[20,30]。在理想情况下,足够大的神经动力学驱动项(如刺激输入)以任意慢的时间尺度发生(即仅发生在神经雪崩之间的间隔内),大脑表现出纯粹的动态渗透行为[30]。为了理解这个属性,让我们考虑公式5和6的变体,其中耗散项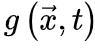 不可忽略,
该公式中的非马尔科夫项
不可忽略,
该公式中的非马尔科夫项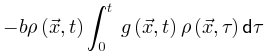 使得神经动力学已经访问过的区域更不可能被激活[20,30]。因此,纯粹的自持活动相消失并被扩展相和非扩展相取代,其中在扩展相中局部扰动可以在整个系统中瞬时传播而不会达到自持状态,而非扩展相中局部扰动永远无法跨越整个系统[20,30]。扩散相和非扩散相之间的相变和相应的临界点νd>νc属于动态渗流的普遍性类别,而不是保守的定向渗流[20,30]。初始神经动力学可以通过时刻0的随机变化来创建[20,30]
其中
使得神经动力学已经访问过的区域更不可能被激活[20,30]。因此,纯粹的自持活动相消失并被扩展相和非扩展相取代,其中在扩展相中局部扰动可以在整个系统中瞬时传播而不会达到自持状态,而非扩展相中局部扰动永远无法跨越整个系统[20,30]。扩散相和非扩散相之间的相变和相应的临界点νd>νc属于动态渗流的普遍性类别,而不是保守的定向渗流[20,30]。初始神经动力学可以通过时刻0的随机变化来创建[20,30]
其中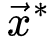 是随机选择的坐标,函数
是随机选择的坐标,函数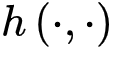 是时刻0的能量驱动函数。每次随机移位后发生神经雪崩时,强耗散项
是时刻0的能量驱动函数。每次随机移位后发生神经雪崩时,强耗散项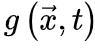 将大脑推向亚临界阶段。因此,大脑无法完全自组织到完美的临界点。相反,大脑只是在临界点νd周围徘徊,形成一个准临界区,在νd两侧表现出有限的波动。然而,在更现实的情况下,驱动项不一定发生在任意慢的时间尺度(即可以发生在任意时刻),神经动力学可能是由保守的定向渗流转变控制,并徘徊在临界点附近。让我们在方程8中添加一个驱动项,
如果我们可以理想地微调驱动项
将大脑推向亚临界阶段。因此,大脑无法完全自组织到完美的临界点。相反,大脑只是在临界点νd周围徘徊,形成一个准临界区,在νd两侧表现出有限的波动。然而,在更现实的情况下,驱动项不一定发生在任意慢的时间尺度(即可以发生在任意时刻),神经动力学可能是由保守的定向渗流转变控制,并徘徊在临界点附近。让我们在方程8中添加一个驱动项,
如果我们可以理想地微调驱动项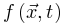 保证
保证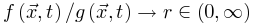 ,则稳定解为
公式10-12对应于
,则稳定解为
公式10-12对应于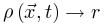 和守恒能量下的大脑稳态,这与 SOC 类似。因此,大脑可能会自组织到SOC临界点νc周围的准临界区域。达到临界点需要理想的微调。这些出现的保守定向渗透行为使科学家能够在实践中以类似于 SOC 的方式识别 SOqC[20,30]。
总而言之,神经科学家可以利用定向渗透理论中的特定工具来大致验证大脑在吸收相和活动相空间中的临界性的存在。这是因为OC、qC、SOC和SOqC在某些条件下表现出或近似表现出定向渗流行为。然而,对于异步相和同步相之间的大脑临界性,普遍性类属性变得相当难以捉摸,因为大脑中同步相变的分析和完整理论仍然不存在[26,33]。尽管在同步相变中可以观察到一些吸收相变的行为,它们之间也存在许多差异[1,23,33]。
和守恒能量下的大脑稳态,这与 SOC 类似。因此,大脑可能会自组织到SOC临界点νc周围的准临界区域。达到临界点需要理想的微调。这些出现的保守定向渗透行为使科学家能够在实践中以类似于 SOC 的方式识别 SOqC[20,30]。
总而言之,神经科学家可以利用定向渗透理论中的特定工具来大致验证大脑在吸收相和活动相空间中的临界性的存在。这是因为OC、qC、SOC和SOqC在某些条件下表现出或近似表现出定向渗流行为。然而,对于异步相和同步相之间的大脑临界性,普遍性类属性变得相当难以捉摸,因为大脑中同步相变的分析和完整理论仍然不存在[26,33]。尽管在同步相变中可以观察到一些吸收相变的行为,它们之间也存在许多差异[1,23,33]。
定向渗流理论预测的大脑临界性有许多性质,其中神经雪崩指数(寿命和尺寸分布的幂律指数)、标度关系、普适塌陷形状和自相关的缓慢衰减都适用于分析推导和根据经验数据进行统计估计(具体推导见原文和图3)。这些属性是我们的主要关注点。为了方便起见,我们在讨论理论细节之前总结了重要的术语表和符号约定(表 2)。
正如我们上面提到的,当大脑处于临界点时,神经雪崩预计会在其寿命和大小分布中表现出幂律特性[25,31,34]。现有的不同理论推导神经雪崩指数的关键思想是确认理想条件下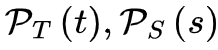 的准确形式。在实际情况中,由于大脑是一个有限系统而寿命和大小受到限制,可能会观察到与理想值的轻微偏差,但神经雪崩指数的理论推导原则上成立。
的准确形式。在实际情况中,由于大脑是一个有限系统而寿命和大小受到限制,可能会观察到与理想值的轻微偏差,但神经雪崩指数的理论推导原则上成立。
图3 大脑临界分析理论预测的神经雪崩特性的概念图 (A)神经雪崩指数的框架图示。(B)平均场假设下神经雪崩满足的缩放关系的图示。(C)神经雪崩普适塌陷形状的图示。t与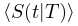 的非标度图(左上)和标度图
的非标度图(左上)和标度图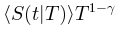 与t/T(右上)用于比较。这里1/T和T1–γ分别作为x轴和y轴上的比例因子,以创建通用的塌陷形状。同时,还给出了平均场框架下的对称塌陷形状(左下)和时间不对称性下由偏度c控制的非对称塌陷形状(右下)。(D)显示了临界(左)和非临界(右)情况下的自相关及其衰减。自相关是在随机选择
与t/T(右上)用于比较。这里1/T和T1–γ分别作为x轴和y轴上的比例因子,以创建通用的塌陷形状。同时,还给出了平均场框架下的对称塌陷形状(左下)和时间不对称性下由偏度c控制的非对称塌陷形状(右下)。(D)显示了临界(左)和非临界(右)情况下的自相关及其衰减。自相关是在随机选择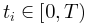 作为参考(左上和右上)后计算的。同时,对
作为参考(左上和右上)后计算的。同时,对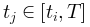 上测量的自相关衰减进行拟合,得出系数
上测量的自相关衰减进行拟合,得出系数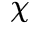 (x 轴对应于
(x 轴对应于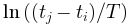 ) 和 ξ(x 轴对应于
) 和 ξ(x 轴对应于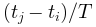 ) (左下和右下)。可以看出,临界情况下的自相关性比非临界情况下的自相关性衰减更慢(
) (左下和右下)。可以看出,临界情况下的自相关性比非临界情况下的自相关性衰减更慢(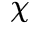 , ξ更小)。
, ξ更小)。
然而,目前雪崩指数的分析还存在以下三个问题:首先,已知的雪崩寿命和大小指数的推导只能在定向渗流的平均场下成立,在推导中如粒度、网络拓扑和神经动力学变异性都可能影响雪崩指数的数值[20,29]。其次,仅确定幂律指数不足以验证大脑临界性的存在,即使实际值与理论预测完全一致,也需要满足标度关系、普适塌陷等。同时,在实践中,幂律指数的统计估计也很容易出错。第三,除非提供额外信息,否则也无法仅根据幂律指数确认或反驳大脑临界性具体的类型。尽管四种类型的大脑临界性在某些条件下表现出(例如,OC)或近似表现出(例如,qC、SOC和SOqC)定向渗流行为,但这些先决条件在实践中很难验证。
虽然通过大脑临界物理理论分析预测的神经雪崩的大多数特性可以通过传统的统计技术来估计,但存在一些经常意味着严重有效性问题的特性,值得特别关注。首先神经雪崩指数的估计是大脑临界性分析中最容易出错的步骤,最小二乘法在拟合幂律数据时被滥用,并且经常得出非常不准确的结果[35,36]。另一个容易出错的步骤是通用塌陷形状的计算和评估。在大多数情况下,塌陷性质的优度评估是非常主观的,为了控制噪声预处理数据的阈值也对大脑临界性分析是不可忽视的影响[37]。最后,自相关缓慢衰减的分析在实践中也无法明确判断衰减是否真正缓慢的标准。
在该综述中,研究者从神经科学的术语重新建立了四种大脑临界性的理论框架并说明了目前神经雪崩研究临界性的局限和容易出错的细节。正如我们所指出的,关于临界性争议的一个不可避免的原因是通过分析得出大脑临界性的物理理论和从经验数据估计大脑临界性的统计技术的非平凡性。过度忽略这些理论基础,尤其是它们的不完善,在实践中可能会导致大脑临界性的精确含义、识别标准和生物学推论的混乱。
对于未来的研究方向,我们认为统计物理理论定义的非平衡动态过程和潜在临界性非常适用于表征大脑功能。研究者可以利用与大脑临界性相关的众多统计物理理论(如定向渗透、保守定向渗透以及动态渗流理论)来进一步区分四种临界性,并与大规模神经动力学实验数据结合。同时也有可能应用与诸如人工神经网络中的临界行为。总之,对大脑临界性进行充分验证的研究有潜力极大地加深我们对神经动力学特征及其在神经信息处理中的作用的理解。奠定扎实的理论基础是为这一蓬勃发展的研究领域做出贡献的最有效和不可或缺的途径。
[1] Fontenele, A. J., de Vasconcelos, N. A., Feliciano, T., Aguiar, L. A., Soares-Cunha, C., Coimbra, B., … Copelli, M. (2019). Criticality between cortical states. Physical Review Letters, 122(20), 208101.
[2] Antonopoulos, C. G. (2016). Dynamic range in the C. elegans brain network. Chaos: An Interdisciplinary Journal of Nonlinear Science, 26(1), 013102.
[3] Li, X., & Small, M. (2012). Neuronal avalanches of a self-organized neural network with active-neuron-dominant structure. Chaos: An Interdisciplinary Journal of Nonlinear
[4] Shew, W. L., Yang, H., Yu, S., Roy, R., & Plenz, D. (2011). Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. Journal of Neuroscience, 31(1), 55–63.
[5] Beggs, J. M., & Plenz, D. (2003). Neuronal avalanches in neocortical circuits. Journal of Neuroscience, 23(35), 11167–11177.
[6] Dalla Porta, L., & Copelli, M. (2019). Modeling neuronal avalanches and long-range temporal correlations at the emergence of collective oscillations: Continuously varying exponents mimic m/eeg results. PLoS Computational Biology, 15(4), e1006924.
[7] Fosque, L. J., Williams-García, R. V., Beggs, J. M., & Ortiz, G. (2021). Evidence for quasicritical brain dynamics. Physical Review Letters, 126(9), 098101.
[8] Fosque, L. J., Williams-García, R. V., Beggs, J. M., & Ortiz, G. (2021). Evidence for quasicritical brain dynamics. Physical Review Letters, 126(9), 098101.
[9] Tkačik, G., Mora, T., Marre, O., Amodei, D., Palmer, S. E., Berry, M. J., & Bialek, W. (2015). Thermodynamics and signatures of criticality in a network of neurons. Proceedings of the National Academy of Sciences, 112(37), 11508–11513.
[10] Gnesotto, F. S., Mura, F., Gladrow, J., & Broedersz, C. P. (2018). Broken detailed balance and non-equilibrium dynamics in living systems: A review. Reports on Progress in Physics, 81(6), 066601.
[11] Lynn, C. W., Cornblath, E. J., Papadopoulos, L., Bertolero, M. A., & Bassett, D. S. (2021). Broken detailed balance and entropy production in the human brain. Proceedings of the National Academy of Sciences, 118(47), e2109889118.
[12] Perl, Y. S., Bocaccio, H., Pallavicini, C., Pérez-Ipiña, I., Laureys, S., Laufs, H., … Tagliazucchi, E. (2021). Nonequilibrium brain dynamics as a signature of consciousness. Physical Review E, 104(1), 014411.
[13] Stewart, C. V., & Plenz, D. (2006). Inverted-U profile of dopamine–NMDA-mediated spontaneous avalanche recurrence in superficial layers of rat prefrontal cortex. Journal of Neuroscience, 26(31), 8148–8159.
[14] Stewart, C. V., & Plenz, D. (2008). Homeostasis of neuronal avalanches during postnatal cortex development in vitro. Journal of Neuroscience Methods, 169(2), 405–416.
[15] Levina, A., Herrmann, J. M., & Geisel, T. (2007). Dynamical synapses causing self-organized criticality in neural networks. Nature Physics, 3(12), 857–860.
[16] Chialvo, D. R. (2010). Emergent complex neural dynamics. Nature Physics, 6(10), 744–750.
[17] Williams-García, R. V., Moore, M., Beggs, J. M., & Ortiz, G. (2014). Quasicritical brain dynamics on a nonequilibrium Widom line.
[18] Malcai, O., Shilo, Y., & Biham, O. (2006). Dissipative sandpile models with universal exponents. Physical Review E, 73(5), 056125.
[19] Bonachela, J. A., De Franciscis, S., Torres, J. J., & Muñoz, M. A. (2010). Self-organization without conservation: Are neuronal avalanches generically critical? Journal of Statistical Mechanics: Theory and Experiment, 2010(2), P02015.
[20] Bonachela, J. A., & Muñoz, M. A. (2009). Self-organization without conservation: True or just apparent scale-invariance? Journal of Statistical Mechanics: Theory and Experiment, 2009(9), P09009.
[21] Rubinov, M., Sporns, O., Thivierge, J.-P., & Breakspear, M. (2011). Neurobiologically realistic determinants of self-organized criticality in networks of spiking neurons. PLoS Computational Biology, 7(6), e1002038.
[22] De Arcangelis, L., Perrone-Capano, C., & Herrmann, H. J. (2006). Self-organized criticality model for brain plasticity. Physical Review Letters, 96(2), 028107.
[23] Girardi-Schappo, M., Galera, E. F., Carvalho, T. T., Brochini, L., Kamiji, N. L., Roque, A. C., & Kinouchi, O. (2021). A unified theory of E/I synaptic balance, quasicritical neuronal avalanches and asynchronous irregular spiking. Journal of Physics: Complexity, 2(4), 045001.
[24] Ma, Z., Turrigiano, G. G., Wessel, R., & Hengen, K. B. (2019). Cortical circuit dynamics are homeostatically tuned to criticality in vivo. Neuron, 104(4), 655–664.
[25] Larremore, D. B., Carpenter, M. Y., Ott, E., & Restrepo, J. G. (2012). Statistical properties of avalanches in networks. Physical Review E, 85(6), 066131.
[26] di Santo, S., Villegas, P., Burioni, R., & Muñoz, M. A. (2018). Landau–Ginzburg theory of cortex dynamics: Scale-free avalanches emerge at the edge of synchronization. Proceedings of the National Academy of Sciences, 115(7), E1356–E1365.
[27] Acebrón, J. A., Bonilla, L. L., Pérez Vicente, C. J., Ritort, F., & Spigler, R. (2005). The Kuramoto model: A simple paradigm for synchronization phenomena. Reviews of Modern Physics, 77, 137–185.
[28] Cocchi, L., Gollo, L. L., Zalesky, A., & Breakspear, M. (2017). Criticality in the brain: A synthesis of neurobiology, models and cognition. Progress in Neurobiology, 158, 132–152.
[29] Girardi-Schappo, M. (2021). Brain criticality beyond avalanches: Open problems and how to approach them. Journal of Physics: Complexity, 2(3), 031003.
[30] Buendía, V., di Santo, S., Bonachela, J. A., & Muñoz, M. A. (2020a). Feedback mechanisms for self-organization to the edge of a phase transition. Frontiers in Physics, 8, 333.
[31] Hinrichsen, H. (2000). Non-equilibrium critical phenomena and phase transitions into absorbing states. Advances in Physics, 49(7), 815–958.
[32] Henkel, M., Hinrichsen, H., Lübeck, S., & Pleimling, M. (2008). Non-equilibrium phase transitions (Vol. 1). Berlin, Germany: Springer.
[33] Buendía, V., Villegas, P., Burioni, R., & Muñoz, M. A. (2021). Hybrid-type synchronization transitions: Where incipient oscillations, scale-free avalanches, and bistability live together. Physical Review Research, 3(2), 023224.
[34] Lübeck, S. (2004). Universal scaling behavior of non-equilibrium phase transitions. International Journal of Modern Physics B, 18(31n32), 3977–4118.
[35] Clauset, A., Shalizi, C. R., & Newman, M. E. (2009). Power-law distributions in empirical data. SIAM Review, 51(4), 661–703.
[36] Virkar, Y., & Clauset, A. (2014). Power-law distributions in binned empirical data. The Annals of Applied Statistics, 8(1), 89–119.
[37] Marshall, N., Timme, N. M., Bennett, N., Ripp, M., Lautzenhiser, E., & Beggs, J. M. (2016). Analysis of power laws, shape collapses, and neural complexity: New techniques and MATLAB support via the NCC toolbox. Frontiers in Physiology, 7, 250.
人类大脑是一个由数以百亿计的神经元相互连接所构成的复杂系统,被认为是「已知宇宙中最复杂的物体」。本着促进来自神经科学、系统科学、信息科学、物理学、数学以及计算机科学等不同领域,对脑科学、类脑智能与计算、人工智能感兴趣的学术工作者的交流与合作,集智俱乐部联合国内外多所知名高校的专家学者发起神经、认知、智能系列读书会第三季——「计算神经科学」读书会,涵盖复杂神经动力学、神经元建模与计算、跨尺度神经动力学、计算神经科学与AI的融合四大模块,并希望探讨计算神经科学对类脑智能和人工智能的启发。读书会从2024年2月22日开始,每周四19:00-21:00进行,持续时间预计10-15周,欢迎感兴趣的朋友报名参与,深入梳理相关文献、激发跨学科的学术火花!
详情请见:计算神经科学读书会启动:从复杂神经动力学到类脑人工智能


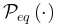 是玻尔兹曼分布。平衡态下,系统状态和之间的转换满足细致平衡条件
是玻尔兹曼分布。平衡态下,系统状态和之间的转换满足细致平衡条件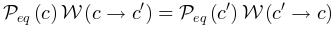 ,其中
,其中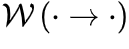 表示转移概率。
表示转移概率。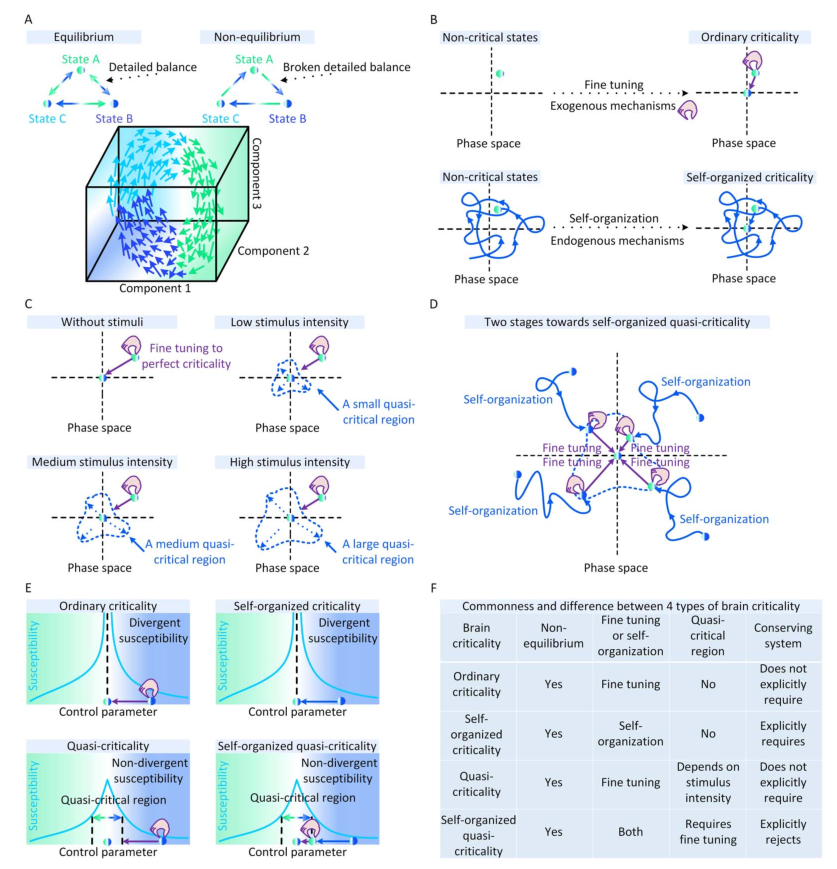
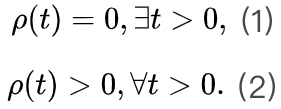
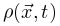 的Langevin方程可以被定义为:
的Langevin方程可以被定义为:
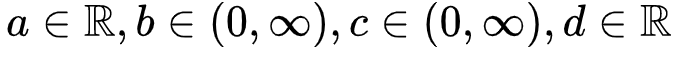 是扩散因子,
是扩散因子,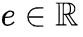 是噪声因子,
是噪声因子,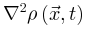 项反映了神经动力学的传播,
项反映了神经动力学的传播,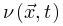 函数定义了根据
函数定义了根据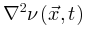 传播的能量(如膜电位),这个函数随着外部驱动
传播的能量(如膜电位),这个函数随着外部驱动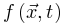 增加,随着体耗散
增加,随着体耗散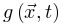 减小。这里我们要求神经元密度和能量始终非负
减小。这里我们要求神经元密度和能量始终非负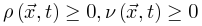 。
。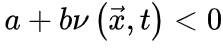 使得神经动力学最终消失(对应吸收相),而
使得神经动力学最终消失(对应吸收相),而 则相反(对应活跃相)。因此,我们可以微调控制参数
则相反(对应活跃相)。因此,我们可以微调控制参数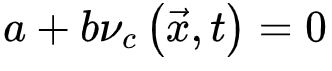 (由νc定义的临界点)处OC。微调依赖于外部机制操纵的
(由νc定义的临界点)处OC。微调依赖于外部机制操纵的 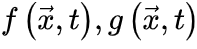 。
。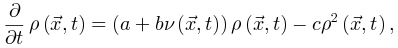 (5)
(5)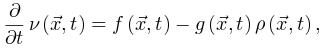 (6)
(6)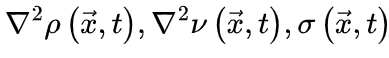 会被忽略。当没有刺激输入。即
会被忽略。当没有刺激输入。即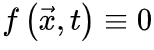 时,活跃和吸收相的临界点是。公式(5,6)的稳定解为
时,活跃和吸收相的临界点是。公式(5,6)的稳定解为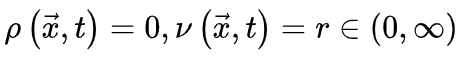
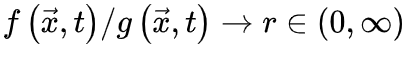 ,此时我们可以导出
,此时我们可以导出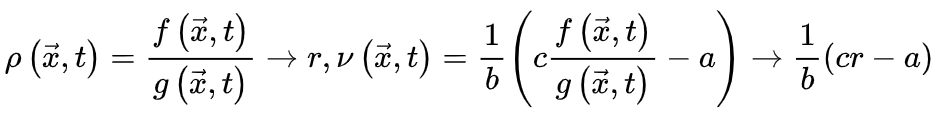
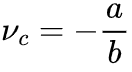 不一定是稳态。除非存在某些理想的外生机制,每当
不一定是稳态。除非存在某些理想的外生机制,每当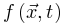 增加时,
增加时,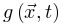 持续增大,否则神经动力学的微调无法消除
持续增大,否则神经动力学的微调无法消除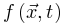 的影响。因此,微调过程可能只能使大脑到达神经动力学敏感性相对较大的准临界区域。最初的OC消失并被qC取代。
的影响。因此,微调过程可能只能使大脑到达神经动力学敏感性相对较大的准临界区域。最初的OC消失并被qC取代。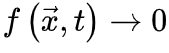 使得
使得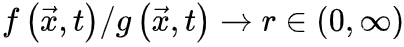 (即时间尺度的无限分离)。因此公式(5,6)的稳态解变为
(即时间尺度的无限分离)。因此公式(5,6)的稳态解变为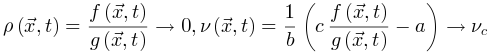
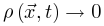 ,此时公式6变为
,此时公式6变为 使得大脑转向活跃相;当大脑处于活跃相,由于
使得大脑转向活跃相;当大脑处于活跃相,由于 公式6变为
公式6变为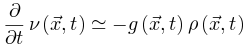 来降低神经动力学。因此这些反馈控制回路将驱使大脑到达临界点。
来降低神经动力学。因此这些反馈控制回路将驱使大脑到达临界点。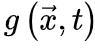 不可忽略,
不可忽略,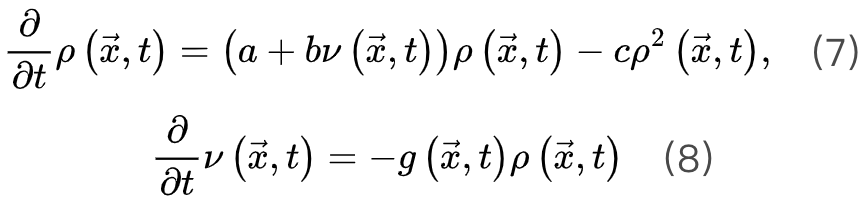
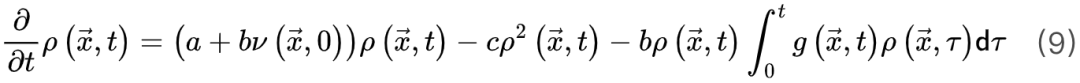
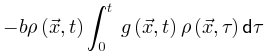 使得神经动力学已经访问过的区域更不可能被激活[20,30]。因此,纯粹的自持活动相消失并被扩展相和非扩展相取代,其中在扩展相中局部扰动可以在整个系统中瞬时传播而不会达到自持状态,而非扩展相中局部扰动永远无法跨越整个系统[20,30]。扩散相和非扩散相之间的相变和相应的临界点νd>νc属于动态渗流的普遍性类别,而不是保守的定向渗流[20,30]。初始神经动力学可以通过时刻0的随机变化来创建[20,30]
使得神经动力学已经访问过的区域更不可能被激活[20,30]。因此,纯粹的自持活动相消失并被扩展相和非扩展相取代,其中在扩展相中局部扰动可以在整个系统中瞬时传播而不会达到自持状态,而非扩展相中局部扰动永远无法跨越整个系统[20,30]。扩散相和非扩散相之间的相变和相应的临界点νd>νc属于动态渗流的普遍性类别,而不是保守的定向渗流[20,30]。初始神经动力学可以通过时刻0的随机变化来创建[20,30]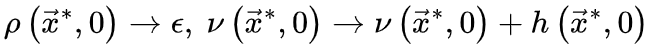
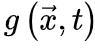 将大脑推向亚临界阶段。因此,大脑无法完全自组织到完美的临界点。相反,大脑只是在临界点νd周围徘徊,形成一个准临界区,在νd两侧表现出有限的波动。然而,在更现实的情况下,驱动项不一定发生在任意慢的时间尺度(即可以发生在任意时刻),神经动力学可能是由保守的定向渗流转变控制,并徘徊在临界点附近。让我们在方程8中添加一个驱动项,
将大脑推向亚临界阶段。因此,大脑无法完全自组织到完美的临界点。相反,大脑只是在临界点νd周围徘徊,形成一个准临界区,在νd两侧表现出有限的波动。然而,在更现实的情况下,驱动项不一定发生在任意慢的时间尺度(即可以发生在任意时刻),神经动力学可能是由保守的定向渗流转变控制,并徘徊在临界点附近。让我们在方程8中添加一个驱动项,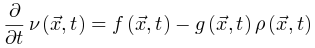
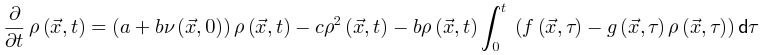
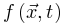 保证
保证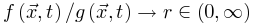 ,则稳定解为
,则稳定解为
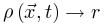 和守恒能量下的大脑稳态,这与 SOC 类似。因此,大脑可能会自组织到SOC临界点νc周围的准临界区域。达到临界点需要理想的微调。这些出现的保守定向渗透行为使科学家能够在实践中以类似于 SOC 的方式识别 SOqC[20,30]。
和守恒能量下的大脑稳态,这与 SOC 类似。因此,大脑可能会自组织到SOC临界点νc周围的准临界区域。达到临界点需要理想的微调。这些出现的保守定向渗透行为使科学家能够在实践中以类似于 SOC 的方式识别 SOqC[20,30]。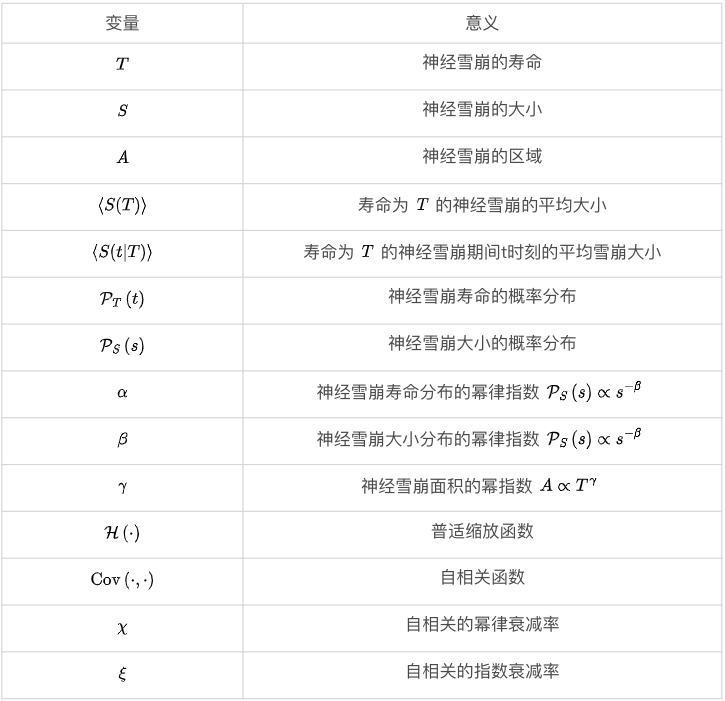
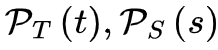 的准确形式。在实际情况中,由于大脑是一个有限系统而寿命和大小受到限制,可能会观察到与理想值的轻微偏差,但神经雪崩指数的理论推导原则上成立。
的准确形式。在实际情况中,由于大脑是一个有限系统而寿命和大小受到限制,可能会观察到与理想值的轻微偏差,但神经雪崩指数的理论推导原则上成立。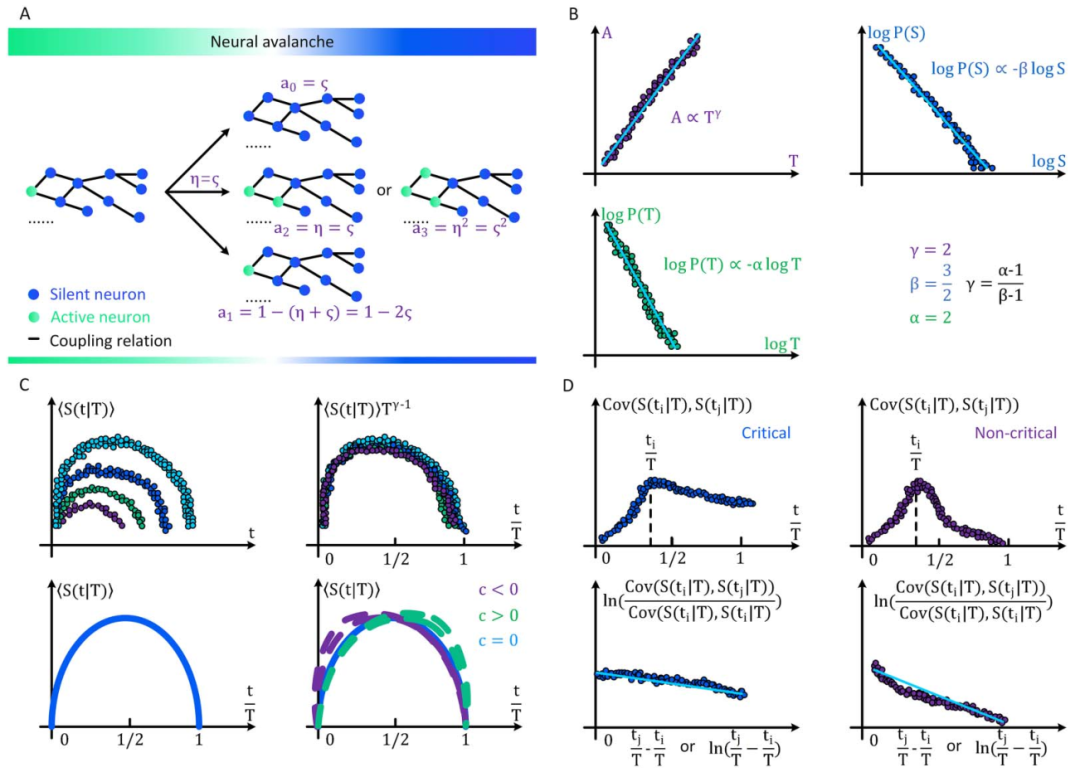
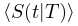 的非标度图(左上)和标度图
的非标度图(左上)和标度图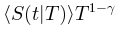 与t/T(右上)用于比较。这里1/T和T1–γ分别作为x轴和y轴上的比例因子,以创建通用的塌陷形状。同时,还给出了平均场框架下的对称塌陷形状(左下)和时间不对称性下由偏度c控制的非对称塌陷形状(右下)。(D)显示了临界(左)和非临界(右)情况下的自相关及其衰减。自相关是在随机选择
与t/T(右上)用于比较。这里1/T和T1–γ分别作为x轴和y轴上的比例因子,以创建通用的塌陷形状。同时,还给出了平均场框架下的对称塌陷形状(左下)和时间不对称性下由偏度c控制的非对称塌陷形状(右下)。(D)显示了临界(左)和非临界(右)情况下的自相关及其衰减。自相关是在随机选择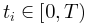 作为参考(左上和右上)后计算的。同时,对
作为参考(左上和右上)后计算的。同时,对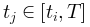 上测量的自相关衰减进行拟合,得出系数
上测量的自相关衰减进行拟合,得出系数![]() (x 轴对应于
(x 轴对应于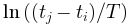 ) 和 ξ(x 轴对应于
) 和 ξ(x 轴对应于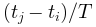 ) (左下和右下)。可以看出,临界情况下的自相关性比非临界情况下的自相关性衰减更慢(
) (左下和右下)。可以看出,临界情况下的自相关性比非临界情况下的自相关性衰减更慢(![]() , ξ更小)。
, ξ更小)。










