站在范畴论视角看机器学习 | 「范畴论与机器学习」系列课程上线
导语

范畴论是什么?
范畴论是什么?
机器学习中的范畴论
机器学习中的范畴论
给定一个输入空间的范畴𝓧,一个输出空间的范畴𝓨,以及一个索引范畴𝓘:
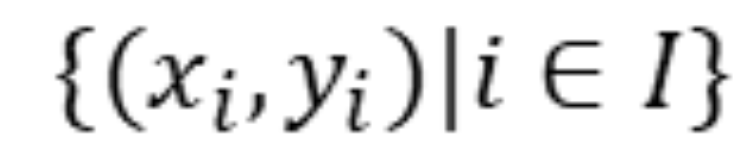 的集合。
的集合。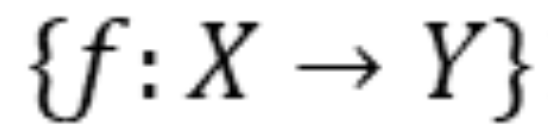 的集合。
的集合。
系列课程简介
系列课程简介
主讲老师
主讲老师


课程框架与大纲
课程框架与大纲
课程框架

课程大纲与简介
第1课:信息的传播:从序理论到范畴
课程简介:
从研究者的角度看,探索未知对象的方法包括两种,一种是把这个对象拆分成原子对象,即不可再拆分的对象,通过研究这些成为原子对象的部分来研究这个对象,这是集合论的思想;另一种是研究这个对象和其他对象之间的“关系”,从而构建出关于这个对象的种种性质的全局的架构,这是范畴论的思想。范畴中强调彰显关系的“箭头”。集合论的思想,实际上能够囊括在范畴论的思想之中。我们将所谓“原子对象”组成“分子”,再组成更大的“结构”,这一过程反映了以未知对象的各级子对象的组成的序。更广泛地,在信息科学中,信息的分解与整合构成序,信息的流动同样构成序。将序的动态过程用箭头描述,就和范畴的理论脱不开渊源。在这节课中,我们将介绍能够非常自然地描述信息科学中各种过程的序,并将这个概念延伸到更加抽象的范畴理论。
主要内容包括:
(1)序理论的基本知识:关系、预序、伽罗瓦连接等
(2)和范畴相关的概念的意义:幺半预序、对称性、预序的充实等
第2课:范畴论基本概念:箭头的学问
课程简介:
范畴广泛出现在数学,物理,以及哲学之中。研究范畴的学科称为范畴论。范畴论在数学的几乎所有分支中都发挥了重要作用,层理论等作为现代数学的重要分支,通过研究某个对象和其他对象之间的关系而研究对象,同时符合深度神经网络等中常见的以网络结构学习的思想。另一方面, 当代范畴论提出了范畴的若干推广, 包括 ∞-范畴的概念, 及由此引出了高阶同伦的思想,高阶关系的构成,提示了许多可能的机器学习的方法论。https://github.com/bgavran/Category_Theory_Machine_Learning?tab=readme-ov-file这一网页中给出了关于范畴思想的机器学习的数十篇论文。为了深入理解它们的思想,本节给出我们学习时必不可少的一些范畴中的初等概念,为大家后续理解论文做好铺垫。
主要内容包括:
(1)如何将数据的集合和数据间的关系统一视为范畴
(2)范畴、函子、自然变换的定义、理解及例子
(3)J-图、极限、余极限、神经的定义、理解及例子
第3课:机器学习理论常用范畴
课程简介:
本节总结机器学习论文中常见的范畴思想,介绍普遍适用的背景范畴,以及常用的具体的范畴,同时深入探讨为什么以这些范畴为背景进行不同机器学习方法论的研究。
主要内容包括:
(1)幺半范畴、充实范畴
(2)笛卡尔微分范畴,引入了光学及透镜的范畴
(3)马尔可夫范畴、准Borel范畴、Kleisli 范畴
第4课:基于梯度的方法的范畴化
课程简介:
本节中介绍基于梯度的机器学习方法,尤其是神经网络的范畴化理论。主要串联下列论文中的思想,比较其中定义的范畴并寻找一致性,同时提供给大家现阶段尚未解决的开放性问题。
-
Categorical Foundations of Gradient-Based Learning
-
Backprop as Functor
-
Lenses and Learners
-
Reverse Derivative Ascent
-
Dioptics
-
Learning Functors using Gradient Descent
-
Compositionality for Recursive Neural Networks
-
Deep neural networks as nested dynamical systems
-
Neural network layers as parametric spans
-
Categories of Differentiable Polynomial Circuits for Machine Learning
第5课:概率方法的范畴化
课程简介:
本节中介绍依赖概率的机器学习方法(如贝叶斯算法等)的范畴化理论。给定的固定数据集下,大多数机器学习问题可以归结为优化问题。而有效解决机器学习问题需要对数据集的来源和限制进行推理。这种机器学习模型中的随机不确定性可以由概率和贝叶斯推理所建模,从而使得监督学习从一个函数逼近问题转变为一个分布逼近问题。通过引入范畴论,可以推理一些范畴内部的随机性,帮助理解概率学习泛性质,并阐明与其他领域的联系。
本节主要串联下列论文中的思想,同时提供给大家现阶段尚未解决的开放性问题。
-
Markov Categories and Entropy
-
Infinite products and zero-one laws in categorical probability
-
A category theory framework for Bayesian Learning
-
Bimonoidal Structure of Probability Monads
-
Representable Markov Categories and Comparison of Statistical
-
Compositional Semantics for Probabilistic Programs with Exact Conditioning
第6课:不变性和等变性学习的范畴化
课程简介:
本节中介绍机器学习的不变性和等变性学习方法的范畴化理论。这一方向的研究集中于机器学习算法的保持对称性的特性。可以使用多种工具来探索数据集的变换与在这些数据集上运行的机器学习模型的输出之间的关系。而许多工具中的范畴论思想非常鲜明,如函子和自然变换。
本节主要串联下列论文中的思想,同时提供给大家现阶段尚未解决的开放性问题。
-
On Characterizing the Capacity of Neural Networks using Algebraic Topology
-
Persistent-Homology-based Machine Learning and its Applications – A Survey
-
Topological Expressiveness of Neural Networks
-
Functorial Manifold Learning
-
Isomorphism, Normalizing Flows, and Density Estimation: Preserving Relationships Between Data
第7课:层,拓扑斯与机器学习
课程简介:
除了定义具体的范畴来研究具体的机器学习方法论之外,也可以泛化地将机器学习中蕴含的思想与现代数学中的前沿代数几何、高阶拓扑及逻辑等联系起来。这一方向深入探讨了数学角度的机器学习中一些网络的基础架构(主要是深度神经网络)与思想,并可能启发基础方法的革新。
课程推荐阅读材料
课程推荐阅读材料
-
第1-3课重点参考:Seven Sketches in Compositionality: An Invitation to Applied Category Theory https://math.mit.edu/~dspivak/teaching/sp18/7Sketches.pdf
-
第4-6课重点参考:Shiebler, Dan, Bruno Gavranović, and Paul Wilson. “Category theory in machine learning.” arXiv preprint arXiv:2106.07032 (2021). https://arxiv.org/abs/2106.07032
-
第7课重点参考:https://www.laurentlafforgue.org/Expose_Lafforgue_topos_AI_ETH_sept_2022.pdf
-
第8课重点参考:Belfiore, Jean-Claude, and Daniel Bennequin. “Topos and stacks of deep neural networks.” arXiv preprint arXiv:2106.14587 (2021). https://arxiv.org/pdf/2106.14587.pdf https://arxiv.org/abs/2106.14587
-
[黎景辉2014] 高等线性代数学。本书以线性代数的思维主线,从矩阵的具体运算发展到抽象代数中的模和模范畴,引入同调代数的方法,最后以范畴论结束。本书以较高的视角重新审视基础的线性代数,需要读者对线性代数、抽象代数有所温习。

-
[李文威2019] 代数学方法(卷一:基础架构)。本书是中文出版观点较为现代的代数学教程,全书贯穿了范畴论的思维方式。对于初学者本书有一定难度,可配合市面上常见的大学代数教材一起学习。

-
学习工具推荐nLab:https://ncatlab.org/nlab/show/HomePage,这是一个关于数学、物理和哲学领域的维基百科,从更高层次的观点来看待问题,包括对同伦论/代数拓扑、同伦类型论、高阶范畴论和高阶范畴代数等工具和视角。
-
学习工具推荐香蕉空间:https://www.bananaspace.org/wiki/%E9%A6%96%E9%A1%B5,一个正在成长的中文数学社区。包括数学百科与数学讲义的网站,但采用更广泛的数学观点,区别于nLab着重范畴论观点。
课程信息
课程信息
课程目的
课程适用对象
-
机器学习领域并且希望深入到理论思想层面;
-
身在数学领域想要利用人工智能解决问题的;
-
希望了解一些范畴论应用前景(例如和人工智能、量子计算融合的可能)。
对学员基础要求
报名须知

加入VIP,解锁集智课程&读书会
集智长期深耕复杂系统与跨学科研究,在网络科学、系统理论、混沌科学等经典领域持续策划精品课程,同时也追踪因果科学、深度学习、复杂经济学、生命复杂性、社会计算、AI+Science、大模型、神经科学、城市科学等交叉前沿。汇集了大量的探索者,包括教授、硕博、工程师、创业者等等。
为了帮助有学习需求的朋友夯实学科基础,帮有科研需求的朋友深入前沿交流,我们开放了1年制和2年制的集智学园VIP计划。VIP用户可以深度参与集智俱乐部社区,并在会员期内解锁集智学园全站课程权限。

推荐阅读:










