上世纪90年代初,朗顿创造了“在混沌边缘计算”这个术语,并开始思考一个难题:系统的复杂性来源于何处。他的文字已经暗示这一迷思与信息理论的紧密关联。Joseph T. Lizier 在 2010 年从悉尼大学获得计算机科学博士学位,在他的博士论文《复杂系统中分布式计算的局部信息动力学》(The Local Information Dynamics of Distributed Computation in Complex Systems)中,接过朗顿提出的挑战,深入信息理论的基础,继续探讨分布式计算与系统复杂性的关系,真正用定量的指标来刻画复杂系统的涌现特征。在这若干年后,人们发现传统信息指标处理多元变量关系的力不从心,于是有了「因果涌现读书会第四季」提到的整合信息分解框架。它继承了 Lizier 的概念和思想,所以回过头来解读这篇博士论文会帮助我们对整合信息分解有更加深刻地理解。
Joseph T. Lizier 的工作在 CORE 博士论文奖中获得了荣誉提名,并被 Springer Theses 收录。该系列论文精选世界各地在相关领域具有重要影响的博士论文,并包含博士生导师对该研究在相关领域影响的介绍(参看文末翻译版本),因而对非专业的跨领域读者也具有较高的可读性。这篇论文的目录如下:
1.引言
2.复杂系统中的计算
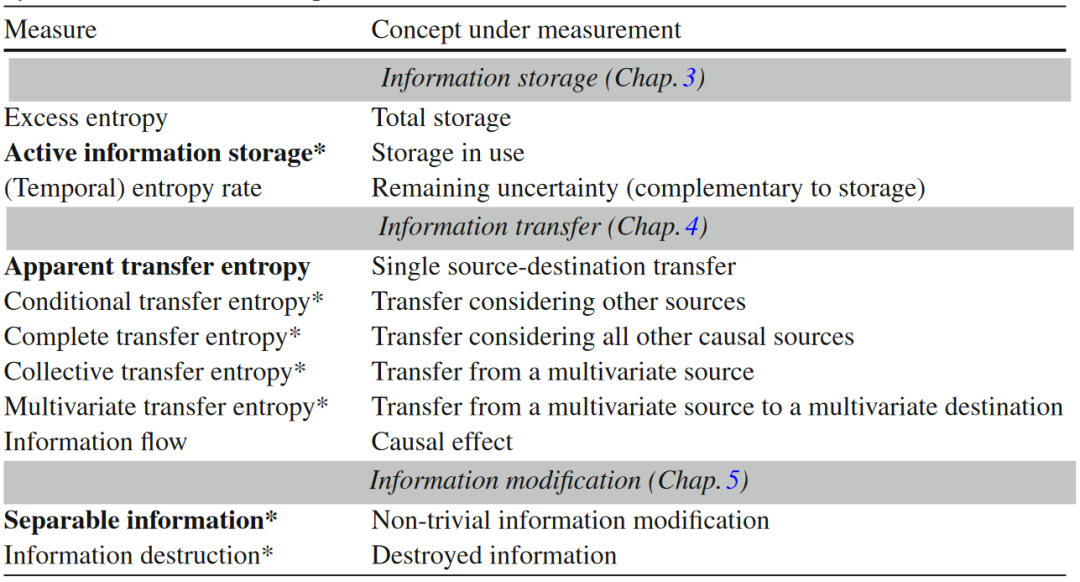
3.信息存储
4.信息转移
5.信息修正
6.网络和相变中的信息动力学
7.复杂计算中的连贯信息结构
8.生物系统中的信息转移
9.总结
我们可以将其分为三大部分,本文主要解读前两章,聚焦问题背景以及复杂系统和信息论的结合;下一期推文将解读三到五章,这是论文最核心的概念框架;最后一期解读六到九章,进一步探讨具体的应用价值。欢迎感兴趣的读者持续关注!
研究领域:复杂系统,信息论,分布式计算,信息动力学,涌现
论文题目:The Local Information Dynamics of Distributed Computation in Complex Systems
论文地址:https://link.springer.com/book/10.1007/978-3-642-32952-4
信息论由香农最早提出,原本应用于密码学与编码领域,为什么对复杂系统的研究要关注信息论,甚至以信息论作为工具呢?
复杂系统可以认为具有两个共通的特征:由大量简单元素或主体组成;元素间存在着不平凡的关系(往往是非线性的)[2]。它描述的可以是任何领域的系统,比如大脑的神经元网络,鸟群,人类族群等等。在每一个单独领域里人类都已积累非常丰富的经验和模型,可我们仍然对一些问题感到困惑:系统的复杂性来自哪里?何以涌现?这些就不是单一学科的模型可以解释的了。于是我们需要一个工具,可以在没有模型假设的情况下,就能够定量刻画复杂系统独有的神奇特征。信息论就可以担当这一角色,绕过复杂的非线性关系,只要能够获取概率分布,就能度量系统内发生的信息变化。而系统的演化能够被各种信息论指标捕捉,正是因为一个复杂系统每时每刻都在进行分布式计算(distributed computation)。
分布式计算指的是系统中的主体们在操作和加工信息。比如蚁群中蚂蚁找到搬运食物最有效率的路径,大脑对信息的处理,鱼群或鸟群中主体对集群运动方向的“计算”,基因调控网络“计算”细胞行为等等。元胞自动机(CA)里,随着时间展开,根据规则可由当前元胞状态计算得出下一时刻所有元胞的状态,这便是一个经典的分布式计算了。由于其规则简洁,已被Wolfram等人进行规则分类,并将分布式计算的概念应用于元胞自动机的研究里,所以它会是本篇文章贯穿始终的研究对象。(不熟悉的读者可自行参阅集智百科中对“元胞自动机”的介绍)
左图:CA:90号规则;右图:CA:184号规则
Joseph T. Lizier 博士在他的博士论文《The Local Information Dynamics of Distributed Computation in Complex Systems》中指出,如果要对分布式计算分个类,可以分为以下三类:信息存储(information storage)、信息转移(information transfer)和信息修正(information modification)。这三个概念最初是由Chris Langton在1990年代早期提出的,用于研究混沌边缘[3],Langton认为,复杂行为和计算能力最大化的系统往往处于有序和混沌之间的相变边缘。后来这些概念在复杂系统研究中被广泛使用。
在后续的推文中我们会分别介绍这三个概念和它们的具体应用,下图是相关信息论指标的概览。
接下来我们来看看,目前信息论已经在复杂系统的研究中有了哪些应用。
如前文所述,信息指标可以度量系统的有序和无序,但不能直接使用香农熵,可以使用熵率来度量系统在时间演化上的不确定程度[4]。而混沌现象最典型的特征便是从底层完全确定的机理中涌现出不确定性。
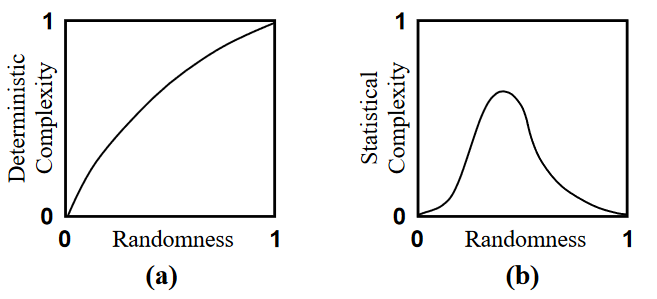
不确定性和系统的复杂程度有一定关联,所以信息论可以用来度量系统的复杂性。通常的直觉是,完全静态有序的过程(具有固定状态)和完全无序或随机的过程(具有完全不可预测的状态)具有最低复杂性。许多复杂性指标试图捕捉这一点,比如统计复杂度(statistical complexity)。这一概念来自于计算力学的研究。相比于下图(a)中的确定性复杂指标(比如柯式复杂度),统计复杂度可以透过观测数据捕捉到其背后的确定的规律。进一步的,这种复杂性度量指标可以用来量化涌现。感兴趣的读者可以参阅往期文章《计算力学:量化涌现的又一条路径》。
如果Langton的判断是对的,即系统在相变时复杂性最大,那么我们就可以使用信息论进行有序-混沌相变的定量研究。比如像沙堆模型、森林火灾等自组织临界相变现象就可以通过某些信息指标的最大化来捕获[5]。而像蚁群中的行为相变现象则由另一些信息指标所度量[6]。需要注意的是,目前没有一个普遍的指标可以度量所有的相变现象,在一些更为复杂的相变中,系统复杂程度也呈现出非单调的变化,而有时候即使没有相变发生,系统的复杂性也会上升[7]。
当复杂性指标和自组织现象高度相关的时候,我们就可以量化一个系统的自组织程度,甚至可以用来构建人工的自组织系统。统计复杂度作为一个经典的复杂性指标,已经被尝试应用在自组织量化研究上了[8]。
纵然信息论的应用已经在系统科学研究中取得很多丰硕的结果,也会存在着对使用信息论的争论。比如美国心理学家Gibson认为信息论不适合应用于自然的系统当中,因为环境不会向生命系统明确地传递信息[9]。但当前学者认为这不是问题,因为环境会隐含地传递信息,反映在系统主体状态的概率分布及其变化里。另一个值得注意的实践上的问题是,很多信息论指标需要大量的数据才能够被准确地计算出来。针对这一问题,我们也有一些计算工具辅助,通过降维来减轻对数据量的要求。核函数估计法和K近邻算法等方法不仅可以适用于有限数量观测数据的情形,还可以用来计算连续变量的信息论指标[10,11]。
信息论作为研究方法,复杂系统作为研究对象,已经形成了基本的研究范式,可以在这个框架下研究许多我们感兴趣的问题,比如涌现、相变等。在接下来的文章中我们会以元胞自动机为核心案例,陆续介绍信息存储、信息转移和信息修正等概念。
最后,我们翻译了 Joseph T. Lizier 的博士导师 Mikhail Prokopenko 为论文撰写的序言,对该研究背后的领域发展有更全面的介绍,分享给大家。我们下一篇见。
导师 Mikhail Prokopenko 的序言
在20世纪90年代初,Chris Langton创造了“在混沌边缘计算”这个术语。他不仅将计算分解为三个基本功能:信息的转移、存储和修正,而且还为在最一般形式下研究计算——信息理论打开了大门。此外,他还提出了一个挑战:如何解释动态环境中计算的涌现,以及它与系统复杂性的关系?
Joseph Lizier 博士的论文,《The Local Information Dynamics of Distributed Computation in Complex Systems》,毫不畏惧地接受了Langton的挑战,深入计算现象的核心,并分析了每个原语的信息理论基础。随后,这些部分以多种方式重新组合,揭示了连贯性和复杂性可能呈现出的不同形态。
这篇论文通过复杂、多样化和动态的领域进行引导,这些领域具有错综复杂的信息处理结构,包括元胞自动机、随机布尔网络、大脑皮层网络、睡眠呼吸暂停中的心率与呼吸频率的相互作用、模块化机器人系统、电力网络中的级联故障等。它揭示了这些系统通过其信息存储(“主动信息存储”)、通信(“信息转移”)和处理(“信息修正”)的连贯性使用,来发挥其内在的功能。
具体而言,主动信息存储(active information storage)用于量化在计算下一个过程状态时直接使用的信息。在元胞自动机中获得的局部主动信息存储的配置文件提供了证据,表明闪烁器(blinkers)和背景域(background domains)是这些系统中的主要存储过程,并且揭示了局部存储有时可能会误导观察者。值得注意的是,该工作引入了局部信息转移(local information transfer)的度量,将其应用于元胞自动机以过滤出斑图(pattern)——该度量首次提供了定量证据,证明了长期以来人们普遍认为的推测,即粒子(比如滑翔机和域壁)是元胞自动机中的主要信息传递实体。这进一步发展成一种新的方法,用于对大脑皮层进行区域间连接分析,使用多元扩展的互信息和转移熵。这种方法的特点在于使用非对称的、多元的信息理论分析,它不仅捕获方向性和非线性关系,还捕获集体交互。
将存储和转移在状态空间中结合起来,这篇论文通过局部信息动态配置文件中的连贯结构(coherent structure)来区分复杂计算,并使用状态空间图来识别复杂计算中的清晰和“隐藏”连贯结构。基于这些度量,通过研究随机布尔网络中从有序到混沌行为的著名相变,他证明在相变点两侧信息存储和信息转移(或连贯转移)均最大化,从而在内在的分布式计算角度解释了这一相变。
触及到因果(causality)这一主题,该研究对比了转移熵和信息流,分别用于量化信息转移和因果信息流,并表明因果信息流是描述系统因果结构的首要工具,而信息转移可以用于描述系统中的涌现计算。随后,该研究在系统的每个空间时间点上量化了信息修正。通过可分离信息(一种新的度量)可以局部地确定,当源变量分离后各自计算时对结果产生误导性的情况(即“整体大于部分之和”的那些点)。
总的来说,这项工作呈现了一个新的子领域——信息动力学(information dynamics)。它使能够严格地描述复杂计算过程中系统内部局部空间时间尺度上的各个组成部分,并为分布式计算和复杂系统的基本性质提供了重要的洞察。
[1] Mediano, P. A. M., Rosas, F., Carhart-Harris, R. L., Seth, A. K., & Barrett, A. B. (2019). Beyond integrated information: A taxonomy of information dynamics phenomena (arXiv:1909.02297). arXiv. http://arxiv.org/abs/1909.02297
[2] M. Prokopenko, F. Boschietti, A.J. Ryan, An information-theoretic primer on complexity, self-organization, and emergence. Complexity 15(1), 11–28 (2009)
[3] C.G. Langton, Computation at the edge of chaos: phase transitions and emergent computation. Phys. D 42(1–3), 12–37 (1990)
[4] D.P. Feldman, C.S. McTague, J.P. Crutchfield, The organization of intrinsic computation: complexity-entropy diagrams and the diversity of natural information processing. Chaos 18(4), 043106 (2008)
[5] M. Prokopenko, P. Wang, P. Valencia, D. Price, M. Foreman, A. Farmer, Self-organizing hierarchies in sensor and communication networks. Artif. Life 11(4), 407–426 (2005)
[6] O. Miramontes, Order-disorder transitions in the behavior of ant societies. Complexity 1(3), 56–60 (1995)
[7] D.P. Feldman, C.S. McTague, J.P. Crutchfield, The organization of intrinsic computation: complexity-entropy diagrams and the diversity of natural information processing. Chaos 18(4), 043106 (2008)
[8] C.R. Shalizi, K.L. Shalizi, R. Haslinger, Quantifying self-organization with optimal predictors. Phys. Rev. Lett. 93(11), 118701 (2004)
[9] J.J. Gibson, The Ecological Approach to Visual Perception (Houghton Mifflin Company, Boston, 1979)
[10] A. Kraskov, H. Stögbauer, P. Grassberger, Estimating mutual information. Phys. Rev. E 69(6), 066138 (2004)
[11] A. Kraskov, Synchronization and interdependence measures and their applications to the electroencephalogram of epilepsy patients and clustering of data, ser. Publication Series of the John von Neumann Institute for Computing. Ph.D. thesis, vol. 24, John von Neumann Institute for Computing, Jülich, 2004.
杨明哲,北京师范大学系统科学学院硕士生,张江老师因果涌现研究小组成员。研究领域是因果涌现、复杂系统自动建模。
学者主页:https://pattern.swarma.org/user/76769
新信息论:从分解到整合
因果涌现读书会第四季招募中
什么是意识?意识能否度量?机器能否产生意识?对于意识问题,人们可能即将迎来一个大的突破,各种有关意识的理论正如雨后春笋般展现出勃勃生机。其中神经科学家 Giulio Tononi 的整合信息论(IID)被认为是最有前景的意识理论之一。如果说意识是大脑神经活动的一种涌现结果,那么刻画涌现便成为理解意识过程中一个重要环节。因果涌现理论目前发展出两个派别,除了 Erik Hoel 的有效信息因果涌现框架,还有一个是 Rosas 的信息分解(PID)框架,此后 Rosas 基于此进一步提出融合整合信息论的信息分解框架 ΦID,尝试构建新的意识理论。
一边是信息整合(IIT),一边是信息分解(PID),看似分裂,实际上都是对香农经典信息论的进一步发展。因果涌现读书会第四季「新信息论:从分解到整合」由北京师范大学系统科学学院教授、集智俱乐部创始人张江老师领衔发起,旨在梳理信息论领域的发展脉络,从香农的经典信息论开始,重点关注整合信息论和信息分解这两个前沿话题,及其在交叉领域的应用。希望通过对这些“新信息论”度量指标的深入探讨,帮助我们理解什么是意识,什么是涌现,并找到不同学科,不同问题背后的统一性原理。
点击“阅读原文”,报名读书会