关键词:混沌,非线性,Lyapunov指数,深度神经网络
论文题目:Finite-Time Lyapunov Exponents of Deep Neural Networks
论文期刊:Physical Review Letters
论文地址:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.057301
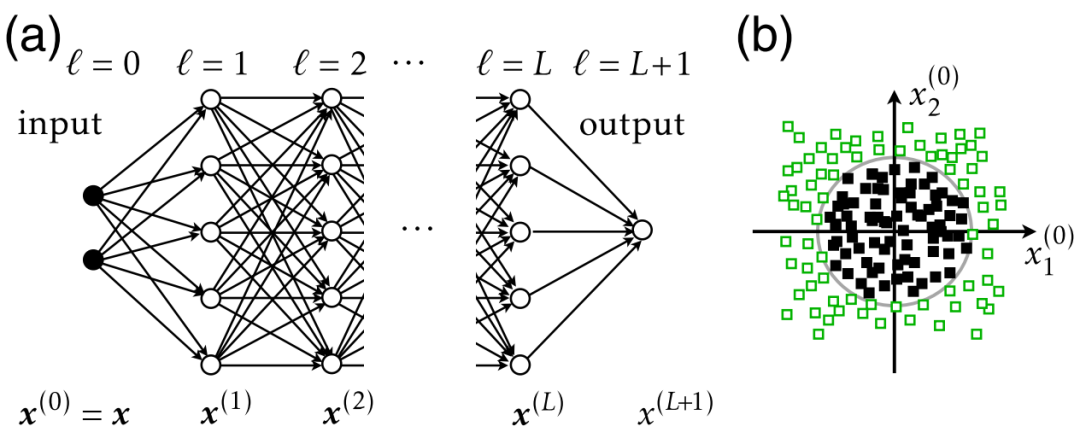
深度神经网络可以被训练用于建模复杂的函数关系。这种神经网络的表现力,即展开复杂的数据结构的能力,随着层数的增加呈指数级增长。最近神经网络的突破性应用使用了具有许多神经元层的深度前馈布局。目前已有研究在无限宽层的渐近极限下进行的数学分析揭示了深层网络如何学习解决分类任务。然而,我们还不知道有限宽度网络何时,以及如何利用其指数级的表现力来表示分类任务所需的数据特征,表示如何影响预测的准确性和不确定性,以及它如何依赖于网络布局。
近日一篇发表在 Physical Review Letters 的研究计算了小的输入扰动如何影响深度神经网络的输出,探索了深度前馈网络与动力系统之间的类比,其中局部扰动的增长或衰减由有限时间的Lyapunov指数所描述。该研究表明,最大指数在输入空间中形成几何结构,类似于动力系统中的相干结构。大正指数的脊线将输入空间分成不同的区域,网络将其与不同类别相关联。这些脊线可视化深度网络在输入空间中构建的几何形状,阐明了其学习能力的基本机制。
研究者考察了在不同分类问题上训练的深度神经网络在输入空间中的有限时间Lyapunov指数的几何结构。在流体力学中,这些拉格朗日相干结构出现为大指数的脊线,并且它们被成功地用来组织复杂时空流动模式的相空间。对于深度神经网络也是如此:FTLE脊线将输入空间划分为与不同类别相关的不同区域。研究者的分析显示了网络如何利用其指数表达能力来形成这些脊线。脊线的锐度决定了离开脊线后分类错误和预测不确定性下降的速度。随着网络宽度的增加,脊线与背景之间的对比消失,导致了一种不同的学习机制,即随机嵌入,其在分类错误和预测不确定性方面具有定性差异。向这种懒惰学习模式的过渡发生在非常宽的网络上,其宽度约为exp(L)。该过渡可能解释了为什么更宽的网络对抗性攻击更加鲁棒:脊线对于表示相关数据结构的重要性越低,实现对抗性攻击就越困难。这里介绍的几何方法可能适用于其他网络架构,如ResNet或Transformer,并且可以帮助可视化和理解这些神经网络学习的机制,但这仍然是一个未来的问题。
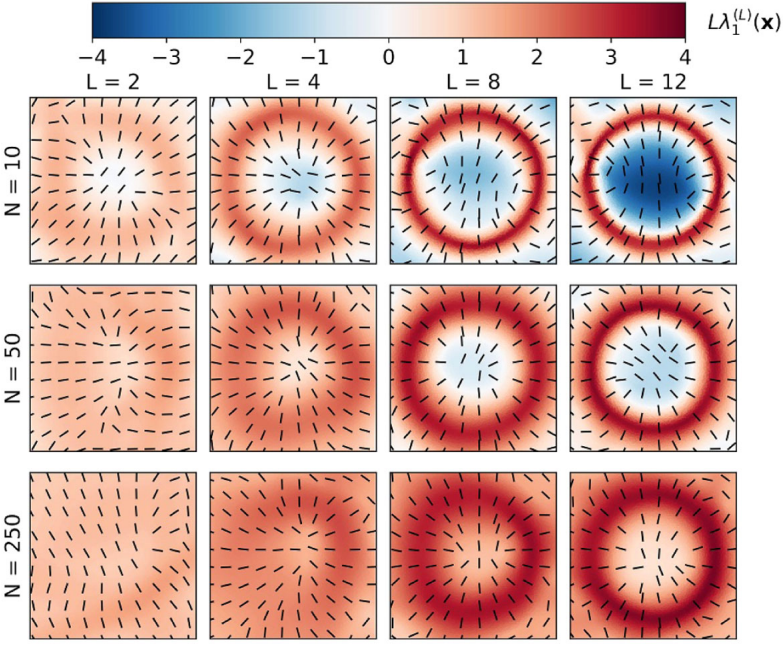
图2 在不同宽度N和深度L的全连接前馈神经网络中,输入空间中的几何 FTLE 结构,这些网络是在图1(b)的数据集上进行训练的。显示了 的大小以及最大的拉伸方向(黑线)。
的大小以及最大的拉伸方向(黑线)。
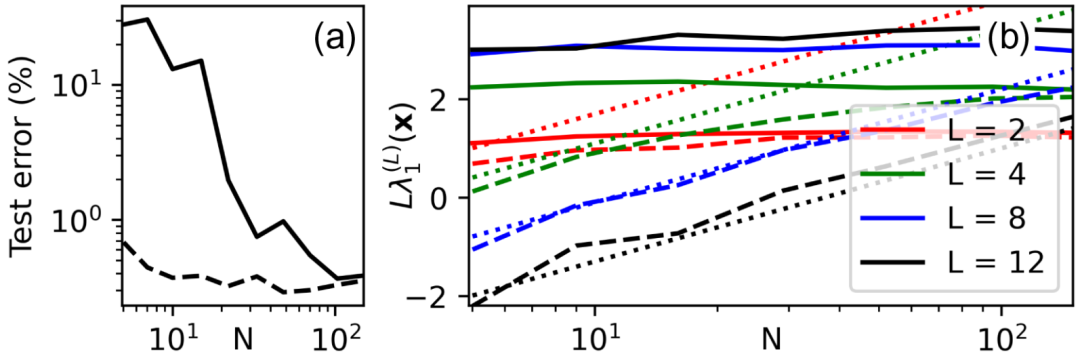
图3 (a) 具有未训练的、随机隐藏权重和经过训练的输出权重的两个隐藏层 L=2 的全连接前馈神经网络在 N 的函数下的分类误差(实线)。同时显示了经过完全训练的网络的分类误差(虚线)。这两条曲线都是对图1中示意的数据集获得的。(b) 对于完全训练的网络,量化在图2中看到的交叉点。显示的是平均值 (实线)和
(实线)和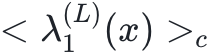 (虚线),详见正文。该数据是通过对独立初始重量实现进行平均获得的。同时,还显示了
(虚线),详见正文。该数据是通过对独立初始重量实现进行平均获得的。同时,还显示了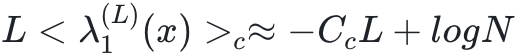 的拟合曲线(点线)。
的拟合曲线(点线)。
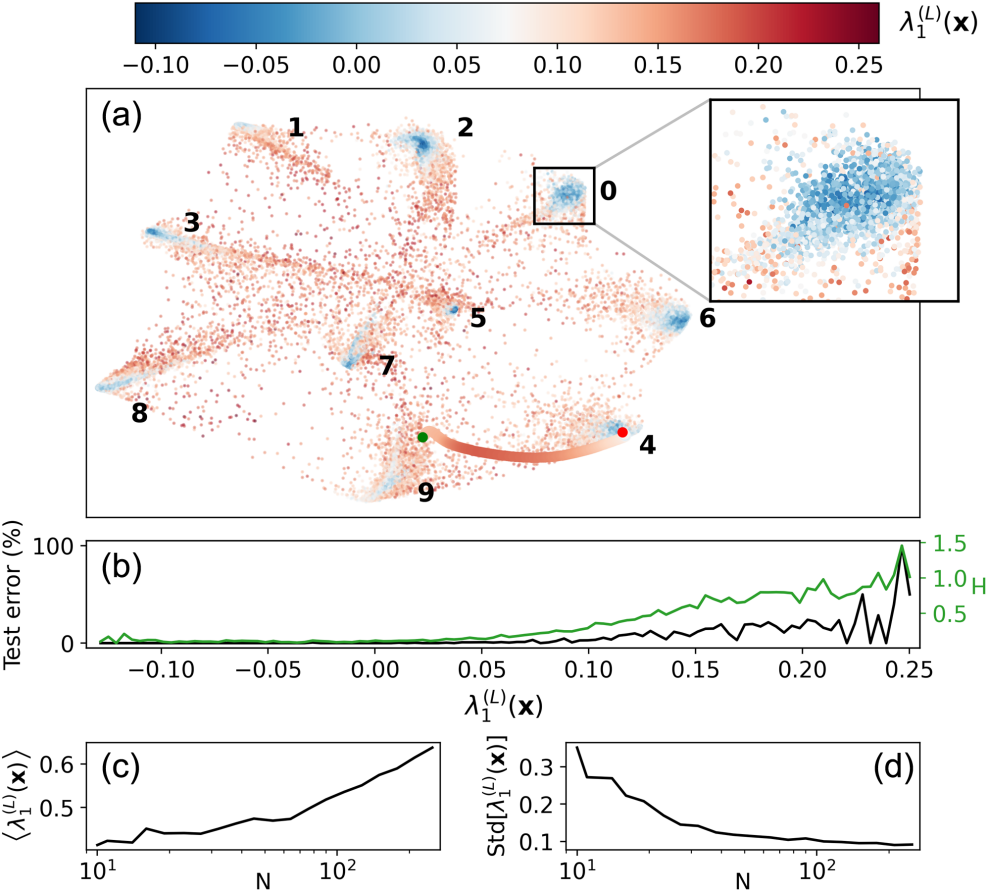
图4 MNIST的最大FTLE场。一个具有每个隐藏层N=20个神经元,L=16个隐藏层和具有十个输出的softmax层的全连接前馈网络被训练到98.88%的分类准确率。对于每个282维输入,计算了最大FTLE并投影到两个维度。(a) 非线性投影中的训练数据。对于每个输入,显示了最大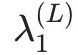 的颜色编码。方框内包含93%的被识别为数字0的样本。还展示了该方框的3倍放大图。彩色线表示从数字9到数字4的对抗攻击,其中以
的颜色编码。方框内包含93%的被识别为数字0的样本。还展示了该方框的3倍放大图。彩色线表示从数字9到数字4的对抗攻击,其中以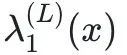 颜色编码。(b) 测试集上的分类错误和预测的不确定性H作为
颜色编码。(b) 测试集上的分类错误和预测的不确定性H作为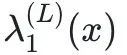 的函数。(c),(d) 最大FTLE分布的均值和标准差与N的变化关系。
的函数。(c),(d) 最大FTLE分布的均值和标准差与N的变化关系。

点击“阅读原文”,报名读书会



 的大小以及最大的拉伸方向(黑线)。
的大小以及最大的拉伸方向(黑线)。
 (实线)和
(实线)和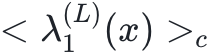 (虚线),详见正文。该数据是通过对独立初始重量实现进行平均获得的。同时,还显示了
(虚线),详见正文。该数据是通过对独立初始重量实现进行平均获得的。同时,还显示了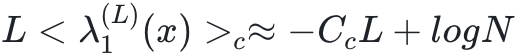 的拟合曲线(点线)。
的拟合曲线(点线)。
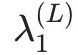 的颜色编码。方框内包含93%的被识别为数字0的样本。还展示了该方框的3倍放大图。彩色线表示从数字9到数字4的对抗攻击,其中以
的颜色编码。方框内包含93%的被识别为数字0的样本。还展示了该方框的3倍放大图。彩色线表示从数字9到数字4的对抗攻击,其中以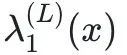 颜色编码。(b) 测试集上的分类错误和预测的不确定性H作为
颜色编码。(b) 测试集上的分类错误和预测的不确定性H作为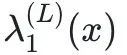 的函数。(c),(d) 最大FTLE分布的均值和标准差与N的变化关系。
的函数。(c),(d) 最大FTLE分布的均值和标准差与N的变化关系。










