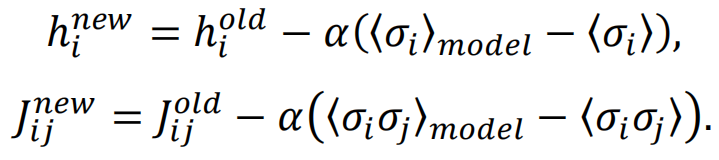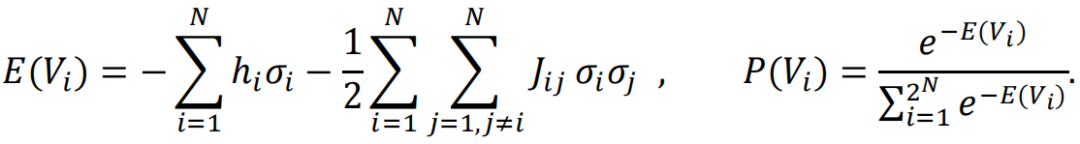复杂系统不仅在变量空间有着极高的自由度,其在参数空间同样也有非常高的自由度。在大量参数不确定的情况下,我们是否仍然可以对系统的动力学情况进行预测?如果错误地估计了某个参数,我们所预测的动力学会跟原来的动力学产生怎样的差异?有趣的是,许多复杂系统的工作状态似乎不会由于部分参数的改变而发生剧烈的变化。例如一个深度学习网络,其中可能包含上千万个参数,但一个能够有较好泛化能力的网络,往往不会因为参数的扰动影响其表现。Sloppy 模型所描述的就是这样一类多参数模型,这类模型的行为只取决于几个参数的严格组合,而参数的其它组合方式对模型预测来说并不重要。这样的模型在生命科学、物理学和人工智能等领域中无处不在。
此次读书会从理论物理的角度出发,结合生物学和信息论的知识,来分析和理解复杂系统背后的数学原理和生物学规律,目的不仅是揭示复杂系统在宏观层面上的简化描述,更是探索这种简化背后的科学原理。读书会中讨论了如何通过Sloppy模型识别系统中的关键参数,量化动力学与稳定性。这样我们可以更好地理解复杂系统的工作机理,以及如何在不同环境和条件下维持其功能。此外还讨论了如何利用这些知识设计更有效的神经科学研究方法,并将这些原理应用于人工智能和其他技术领域。
在物理学中,理想气体的微观粒子虽然自由度高,但宏观上我们可以用温度、压强和体积等简单的量来描述。同样,在生物学中,细菌群体的生长和进化虽然复杂,却也遵循一定的宏观规律。这些现象让我们思考:对于复杂系统,我们能否在宏观层面上用较少的参数来捕捉其主要特征和秩序?
这一问题的答案,或许可以从我们对现实世界的观察中得到启示。例如,当我们观察一幅由随机像素组成的图像时,很难从单个像素推断出周围像素的信息。然而,当我们面对自然界中的图像时,如手写数字或自然风景,却能够轻易地根据一部分信息预测整体的模式。这种能力源自于自然界中的物体和现象之间存在着某种内在的关联性。正是这种关联性,使得我们的世界变得有序,也使得科学探索成为可能。这些观察结果向我们展示了一个关键的事实:尽管世界复杂多变,但它并非随机无序,而是遵循着某种可理解的规律。因此,我们能用宏观上的低自由度来描述高自由度的复杂系统,即只有少数自由度是关键的。这正是Sloppy方法的理论基础。
具体来说,对于像理想气体这样的独立粒子系统,其联合分布可以通过各个独立分布的乘积来表示,例如,描述气体分子运动速率的麦克斯韦-玻尔兹曼分布可以被描述为具有3个自由度的χ分布。而对于非独立粒子系统,它们在宏观层面上的简化主要归因于三个因素。首先,系统本身受到物理和几何约束。其次,复杂系统在形成过程中必须抵抗噪声,并且为了保持其任务表现的泛化能力,不能对每个参数都过于敏感。最后,复杂系统的演化过程中可能出现路径依赖,一些简单的结构一旦出现,就更容易被选择(例如智能手机形态的“趋同进化”)。
为了模拟我们之前讨论的这些特性,一个经典的选择是Ising模型。这个模型最初是为了描述磁性材料的特性而提出的。其数学表达式如下:
其中,σj表示第j个位置处的自旋方向,Jij与μ均为参数。
Ising模型中, 表示相互作用,
表示相互作用,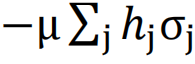 表示个体特征。而神经动力学同样由两个方面的因素所决定,一方面是由神经元本身的某种性质,另一方面是由神经元与神经元之间的某种影响。因此,我们可以使用类似的Ising模型来模拟神经动力学。
表示个体特征。而神经动力学同样由两个方面的因素所决定,一方面是由神经元本身的某种性质,另一方面是由神经元与神经元之间的某种影响。因此,我们可以使用类似的Ising模型来模拟神经动力学。

图片来源:Szekely, P., Sheftel, H., Mayo, A., & Alon, U. (2013). PLoS Comp Biol, 9(8), e1003163.
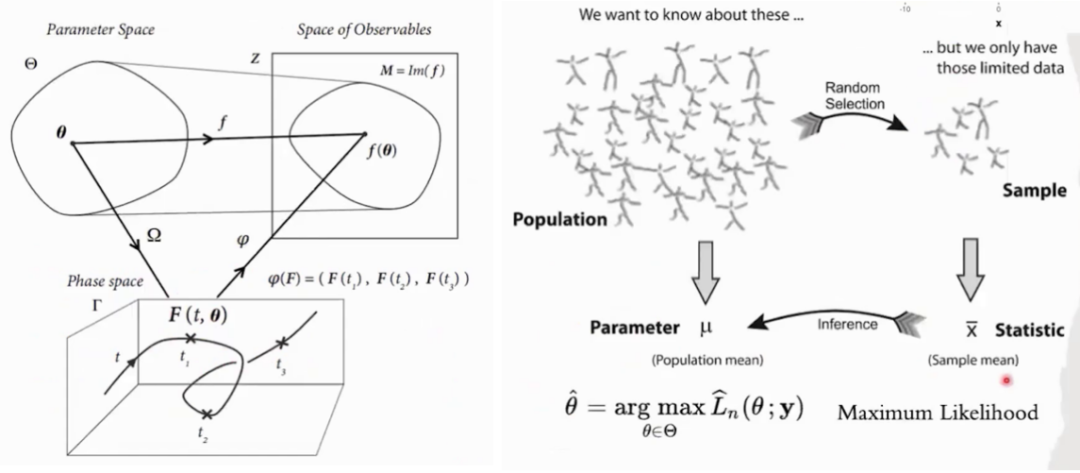
通常我们认为,参数决定了模型的演化,即参数决定动力学。在文献[1]中提到的基因调控网络中,尽管有许多参数,但即使不完全了解这些参数,我们也能把握整个系统的动力学。文中分析了两个参数的取值关系,如果参数取值是无关的,那就应该如上图中d所示,但是实际得到的却是图e,这意味着参数之间有着某种约束。那么为什么会有这种约束呢?因为生物体表现出的动力学并非随机,因此对动力学有特定要求的参数也会受到限制,使得参数的选择最终落在一个更低维的子空间内。
上面的现象使得我们想进一步探讨参数与动力学的关系。在物理学中,参数的不同取值会导致系统随时间演化的差异,进而影响我们观测到的现象。以大脑为例,采用Ising模型建模,它的参数主要描述了大脑不同区域的活跃性以及它们之间的连接情况。而这些参数发生改变,大脑动力学也将对应发生改变。在统计学的视角下,一旦参数确定了,随机变量的分布也就随之确定。例如,只要我们知道均值和方差,就能定义一个高斯分布。这种关系使我们能够通过观测数据来推断参数,这就是参数估计方法的基础。
更一般地,我们考虑参数空间(参数所构成的空间)与行为空间(变量所构成的空间)的关系,如下表。在诸多领域我们都可以发现参数决定了行为,但同时进化又反过来通过选择行为确定了一些参数之间的约束。
这种相互作用促使我们进一步研究参数变化与行为变化之间的关系。我们发现一些参数的改变几乎不会影响动力学,而另外一些参数一旦扰动,动力学将发生巨大改变。于是我们将前者称为Sloppy的参数,而后者敏感性的参数被称为Stiff的。
为了更严格地衡量这种动力学的变化,Sethna提出了一种度量方式[2],公式如下:
该公式计算了在时间t内,系统由θ*变为θ,动力学发生的改变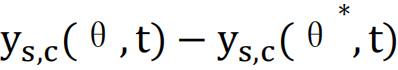 ,并进行归一化处理。
,并进行归一化处理。
基于这些想法,Sethna对多种系统进行了深入研究,提出了Sloppy模型的概念(如下图所示)。大量研究表明,在绝大多数生物系统中,大部分参数都具有Sloppy特性,而只有少数参数扮演着关键角色。
为了定量描述参数的稳定性,我们引入了Fisher信息矩阵,它由参数的二阶导数构成,反映了概率分布的凹凸性(注:这里的讨论简化了问题,严格来说,这种由二阶导数所定义的Fisher信息矩阵为“观测Fisher信息”,即 Observed fisher information)。一个分布的凹凸性越大,表明其越不稳定,蕴含的信息量越大,而这个分布的形状正是由参数决定的。故可以用Fisher信息矩阵描述模型对参数的稳定性。
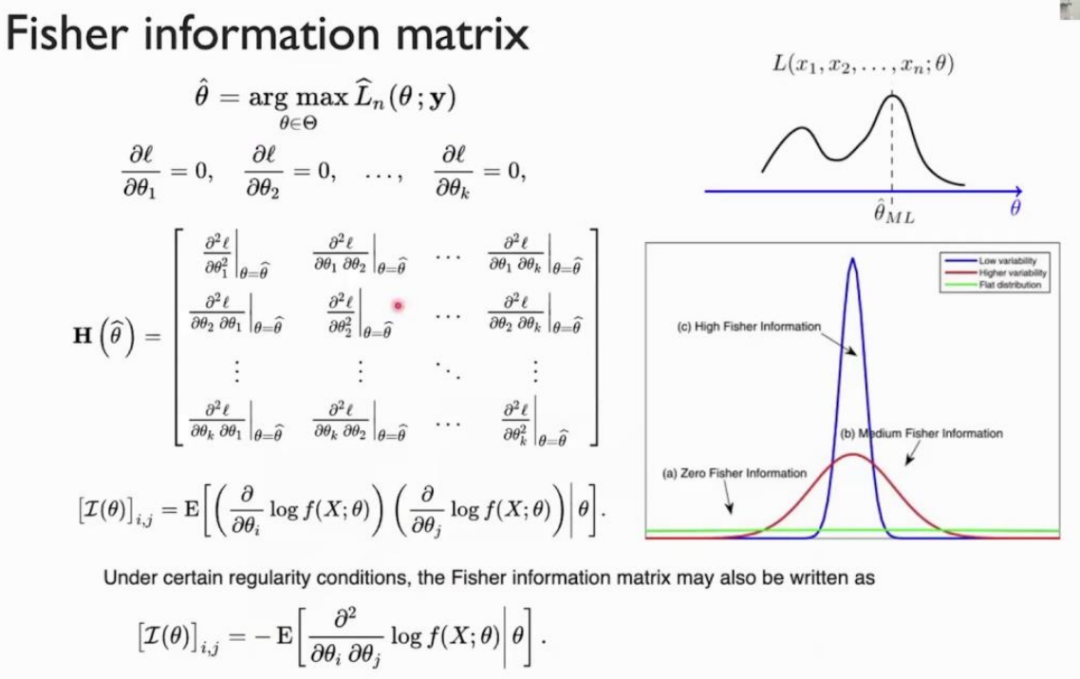
下面我们更直观地来理解Sloppy和Stiff。我们说Sloppy或Stiff的维度或方向,可以不仅仅是某个具体的参数,也可以是参数的组合。数学上的理解就是,对Fisher信息矩阵求特征值和特征向量,其中对应最大特征值的特征向量就是Fisher信息下降最快的方向,相应的参数组合因此对应于能最大程度改变系统动力学的Stiff方向。在大量真实的复杂系统中,Stiff的维度往往远远小于系统的自由度数,这些方向上的扰动将严重影响系统的动力学行为,在相应方向上概率分布函数的投影形状更尖锐,有更小的方差。对于大多数的Sloppy的维度,这些维度上参数的扰动对系统的动力学影响较小,相应方向上概率分布函数的投影更宽扁、更大方差。
这一套基于Fisher信息的语言构成了一个新的学科——信息几何。信息几何背后的理论基础将有助于我们对稳定性进行更深入的数学分析,如我们发现Fisher信息度量可以由KL散度的二阶导导出,这就建立了参数稳定性与KL散度之间的联系。
Sethna在研究Sloppy模型的时候也提出了类似的想法。他采用动力学的变化关于参数对数的二阶导,来描述参数的稳定性[2],计算如下:
以上就是Sloppy模型基本思想的数学描述,唐乾元老师课题组将这套思想用到蛋白质的进化问题的研究上[3],以蛋白质进化过程中的突变作为参数,蛋白质的动力学作为变量,发现了蛋白质动力学与进化之间存在一种对应关系。想要更具体地了解论文的详细内容,请阅读文献[3]。
我们常常依赖于模型来解释观察到的现象。然而,在实际的建模过程中,往往需要从现象出发,反向推导出模型参数。例如,AlphaFold预测蛋白质结构,它通过分析同家族蛋白质序列不同位点间突变的关联性来推断氨基酸的相对位置。同样,在构建脑网络时,我们也需要通过分析不同脑区信号的关联性来推断网络的结构。
在这个过程中,求解逆问题——即从现象倒推参数——是至关重要的一步。为了实现这一目标,一种常用的方法是最大熵模型。最大熵模型的核心思想是在最大不确定性(亦即最少假设)的前提下估计参数,同时,如果系统本身带有约束,我们可以通过拉格朗日乘子在数学上引入这些约束。例如,如果我们已知一个系统的均值和方差,那么利用最大熵原理,我们可以得出该系统遵循高斯分布。对于其他常见的概率分布及其对应的最大熵约束,可以参考维基百科的相关条目 (Maximum entropy probability distribution) [7]。
在具体的实验中,研究者们使用了基于大脑的BOLD信号[4]和神经信号发放[5]的数据。通过最大熵模型,能够计算出模型预测的均值和方差,并与实际数据的均值和方差进行比较。并通过下面的规则进行迭代,最终学习到相应的参数:
在这个学习过程中,模型学习了两个关键的元素:与节点活跃度相关的hi和与连边强度相关的Jij。此外,文献还发现:如果模型忽略了连边Jij,其效果会有所下降;而当同时考虑hi和Jij时,即得到了所谓的pairwise最大熵模型(MEM),模型的表现得到了显著提升。pairwise最大熵模型的数学表示如下:
对该模型进一步进行简化的假设,就可以得到Ising模型。此外,得到参数之后可以使用蒙特卡洛方法来模拟Ising模型,以验证模型的有效性。
在《eLife》发表的一篇文章中[6],研究者使用老鼠听觉皮层A1区域的信号发放数据,也对比了pairwise MEM与独立模型(independent model)。而在《Nature Communications》的另一篇文章中[4],研究者还对比了另外两种方法:直接求逆的高斯模型(inverse Gaussian model)和求逆后进行归一化的偏相关方法(Partial correlation method)。他们在默认模式网络(DMN)和额顶网络(FPN)上,采用了pairwise MEM、inverse Gaussian model、Partial correlation method以及互信息方法,通过与解剖连接、功能连接的比较,进行了相关的分析,验证了pairwise MEM在构建脑网络模型中的优越性。
在《Journal of Neuroscience》发表的一篇文章中[5],研究者们对离体培养的神经组织进行了深入研究。他们的工作集中在两个主要方面:首先,他们检验了模型拟合参数的准确性;其次,他们利用Fisher信息来评估参数的稳定性,即判断参数是Sloppy还是Stiff。
Fisher信息的高低直接关联到参数的稳定性,信息越高,参数越Stiff,系统越不稳定。研究者们特别关注了与此相关的特征向量,因为它们在理解系统行为中扮演着重要角色。通过选择具有最大Fisher信息的几个特征向量,他们能够识别出对系统影响最大的参数。
为了进一步分析参数的分布特性,研究者们引入了Gini系数,这是一个衡量公平性的指标,也可以用来刻画Fisher信息矩阵的稀疏程度。Gini系数越大,意味着Stiff参数越少,Sloppy参数越多,这为理解系统的稳定性提供了新的视角。此外,通过研究网络参数在Fisher信息矩阵特征向量上的投影,他们验证了模型参数在特定方向的Sloppy和Stiff特性,并基于LIF神经元模型从理论的角度进一步验证了其理论。
在另一篇文章中[6],研究者们发现,尽管参数和参数的变化量可能不稳定,但Fisher信息矩阵的特征向量却是相对稳定的。通过对Fisher信息的矩阵元统计、特征值统计、参数变化在Fisher信息矩阵特征向量上的投影等进行分析,他们揭示出不同小鼠的实验结果中的一致性结论。主要包含下面两个重要的结论:
-
首先,沿着Stiff方向的改变主要与皮层状态的切换有关;
-
其次,系统在保持原始工作状态下对刺激信号做出的响应与Sloppy方向有关。
此外,他们还发现,网络中经常作为枢纽的节点与敏感性的Stiff参数相对应。唐老师在报告中指出,这种现象非常类似于各种自组装现象中,整体系统的熵增与局部的熵减之间的统一。他认为,随着复杂系统的演化,系统作为一个整体可能会在学习、适应、进化等演化过程中获得更多的Sloppiness,与此同时,系统的“核心”部分则有可能会出现更高度的Stiffness。
最后,唐老师总结了参数空间与行为空间之间敏感性与稳定性之间的对应关系。在许多实例中,参数空间的敏感性往往与行为空间的稳定性相对应;而参数空间的稳定性(即sloppiness)往往与行为空间中的敏感性相关。基于这些理论,他对蛋白质突变的稳定性和功能的敏感性进行了一些研究,对这些研究感兴趣的朋友们,可以进一步查阅文献资料[8][9]。
参考文献
[1] Szekely P, Sheftel H, Mayo A, et al. Evolutionary tradeoffs between economy and effectiveness in biological homeostasis systems[J]. PLoS computational biology, 2013, 9(8): e1003163.
[2] Gutenkunst R N, Waterfall J J, Casey F P, et al. Universally sloppy parameter sensitivities in systems biology models[J]. PLoS computational biology, 2007, 3(10): e189.
[3] Tang Q Y, Kaneko K. Dynamics-evolution correspondence in protein structures[J]. Physical review letters, 2021, 127(9): 098103.
[4] Watanabe T, Hirose S, Wada H, et al. A pairwise maximum entropy model accurately describes resting-state human brain networks[J]. Nature communications, 2013, 4(1): 1370.
[5] Panas D, Amin H, Maccione A, et al. Sloppiness in spontaneously active neuronal networks[J]. Journal of Neuroscience, 2015, 35(22): 8480-8492.
[6] Ponce-Alvarez A, Mochol G, Hermoso-Mendizabal A, et al. Cortical state transitions and stimulus response evolve along stiff and sloppy parameter dimensions, respectively[J]. Elife, 2020, 9: e53268.
[7] https://en.wikipedia.org/wiki/Maximum_entropy_probability_distribution
[8] Tang Q Y, Hatakeyama T S, Kaneko K. Functional sensitivity and mutational robustness of proteins[J]. Physical Review Research, 2020, 2(3): 033452.
[9] Tang Q Y, Kaneko K. Dynamics-evolution correspondence in protein structures[J]. Physical review letters, 2021, 127(9): 098103.


相关工作报道
参看在因果涌现与生命复杂性读书会的更多分享:
-
Sloppy Model:复杂系统中稳定的宏观规则的涌现
https://pattern.swarma.org/study_group_issue/139
https://pattern.swarma.org/study_group_issue/68
人类大脑是一个由数以百亿计的神经元相互连接所构成的复杂系统,被认为是「已知宇宙中最复杂的物体」。本着促进来自神经科学、系统科学、信息科学、物理学、数学以及计算机科学等不同领域,对脑科学、类脑智能与计算、人工智能感兴趣的学术工作者的交流与合作,集智俱乐部联合国内外多所知名高校的专家学者发起神经、认知、智能系列读书会第三季——「计算神经科学」读书会,涵盖复杂神经动力学、神经元建模与计算、跨尺度神经动力学、计算神经科学与AI的融合四大模块,并希望探讨计算神经科学对类脑智能和人工智能的启发。读书会从2024年2月22日开始,每周四19:00-21:00进行,持续时间预计10-15周,欢迎感兴趣的朋友报名参与,深入梳理相关文献、激发跨学科的学术火花!
详情请见:计算神经科学读书会启动:从复杂神经动力学到类脑人工智能




 表示相互作用,
表示相互作用,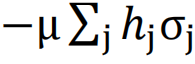 表示个体特征。而神经动力学同样由两个方面的因素所决定,一方面是由神经元本身的某种性质,另一方面是由神经元与神经元之间的某种影响。因此,我们可以使用类似的Ising模型来模拟神经动力学。
表示个体特征。而神经动力学同样由两个方面的因素所决定,一方面是由神经元本身的某种性质,另一方面是由神经元与神经元之间的某种影响。因此,我们可以使用类似的Ising模型来模拟神经动力学。



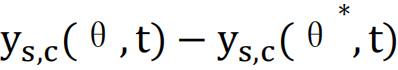 ,并进行归一化处理。
,并进行归一化处理。