热力学与量子力学在21世纪重新相遇

导语

1. 引言
1. 引言
四大力学都有其经典与量子相对应。经典力学对应量子力学,经典电动力学对应量子电动力学,经典统计力学对应量子统计力学,经典场论对应量子场论。唯一的例外就是经典热力学,目前通常的物理专业课程中还没有量子热力学。
在国际单位制中有7个基本单位,其中6个已经可以在微观的原子层面定义。唯一的例外是温度,定义它所采用的玻尔兹曼常数,或者水的相变点,是相对宏观的。我们还无法采用一个更加微观的实验手段来定义温度。
按照热力学的语言,温度反映的是分子的平均动能,而那些难以定义动能的系统,比如自旋系统,它的温度依赖性在这个定义下显得非常晦涩。又或者按照能均分定理,每一个自由度贡献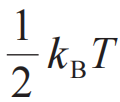 ,对于较为复杂的大分子,这个定义也是失效的。系综理论将系统的温度归结为由环境来决定,但环境本身是一个相对模糊的概念,环境的温度由谁来提供,没有解释。
,对于较为复杂的大分子,这个定义也是失效的。系综理论将系统的温度归结为由环境来决定,但环境本身是一个相对模糊的概念,环境的温度由谁来提供,没有解释。
归根结底,熵难以被实验测定是根本原因。因为强度量一般难以向微观推广,除了温度,压强、化学势的测定方法也相对宏观唯象。作为与温度相对应的广延量,如若熵能在微观层面被准确测定,我们就可以利用能量对熵求导来获得温度。然而经典统计力学利用状态数来定义熵,令这一想法难以实施。
近年来,伴随着量子信息的迅速发展,测量纠缠熵已经不存在原则性的技术障碍。是否能够利用这一新技术来重新诠释热力学中的温熵关系呢?这就涉及如何在量子力学框架内重新定义热,量子热力学这一古老命题因此重焕生机。
2. 自由能与温度
2. 自由能与温度
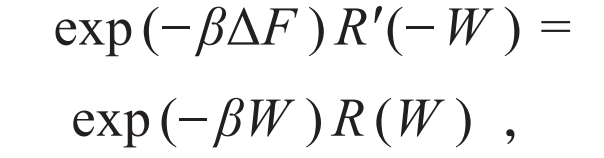
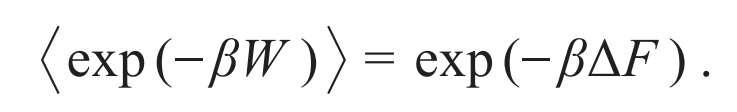
3. 量子混沌
3. 量子混沌
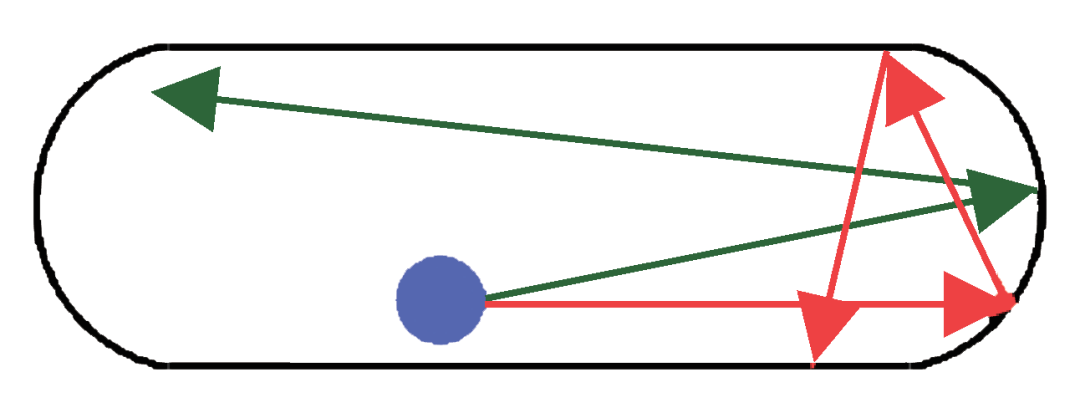
关于混沌的定义,一般应满足如下三个条件:
(1)有界性 (boundedness):其运动范围存在一个确定的边界;
(2)回归性 (recurrence):无论从哪个起点出发,总能不断回到该起点;
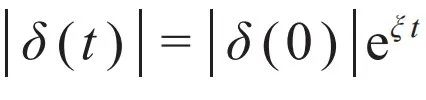 ,其中δ(t)是两条起点相互接近的运动轨迹之差,ξ是Liapunov指数,它为正时就是混沌的。由于运动轨迹有界,所以δ(t)随着时间演化并不会无限增加,而是会逐渐趋于饱和,所以为了真实反映指数敏感性,在实际计算时往往要映射到正切空间,也就是运动轨迹的导数所张成的空间。
,其中δ(t)是两条起点相互接近的运动轨迹之差,ξ是Liapunov指数,它为正时就是混沌的。由于运动轨迹有界,所以δ(t)随着时间演化并不会无限增加,而是会逐渐趋于饱和,所以为了真实反映指数敏感性,在实际计算时往往要映射到正切空间,也就是运动轨迹的导数所张成的空间。
4. 量子热化理论
4. 量子热化理论
 ,第一条是指,它在微正则系综中的平均值,等于其在哈密顿量不同本征态上平均值的等权重求和,即
,第一条是指,它在微正则系综中的平均值,等于其在哈密顿量不同本征态上平均值的等权重求和,即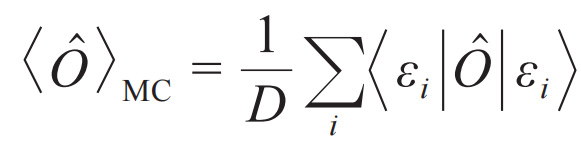 ,其中εi 的取值范围是给定的能量范围[E, E+δ],D代表相应能量范围内量子态的个数。第二条是指,
,其中εi 的取值范围是给定的能量范围[E, E+δ],D代表相应能量范围内量子态的个数。第二条是指, 的非对角元
的非对角元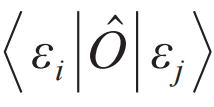 随着εi 和εj 的能量差随机变化并快速衰减至0。
随着εi 和εj 的能量差随机变化并快速衰减至0。 是哈密顿量的某个特定泛函,就自动不满足第一条。或者令
是哈密顿量的某个特定泛函,就自动不满足第一条。或者令 是某个算符的平方,就一定不满足第二条。所以在实际操作时,
是某个算符的平方,就一定不满足第二条。所以在实际操作时, 的选取并不任意,而是要选择自由度较小的局域算符,一般是某个对称性不可约的产生子,从而尽量避免上述问题。
的选取并不任意,而是要选择自由度较小的局域算符,一般是某个对称性不可约的产生子,从而尽量避免上述问题。
5. 局域化
5. 局域化
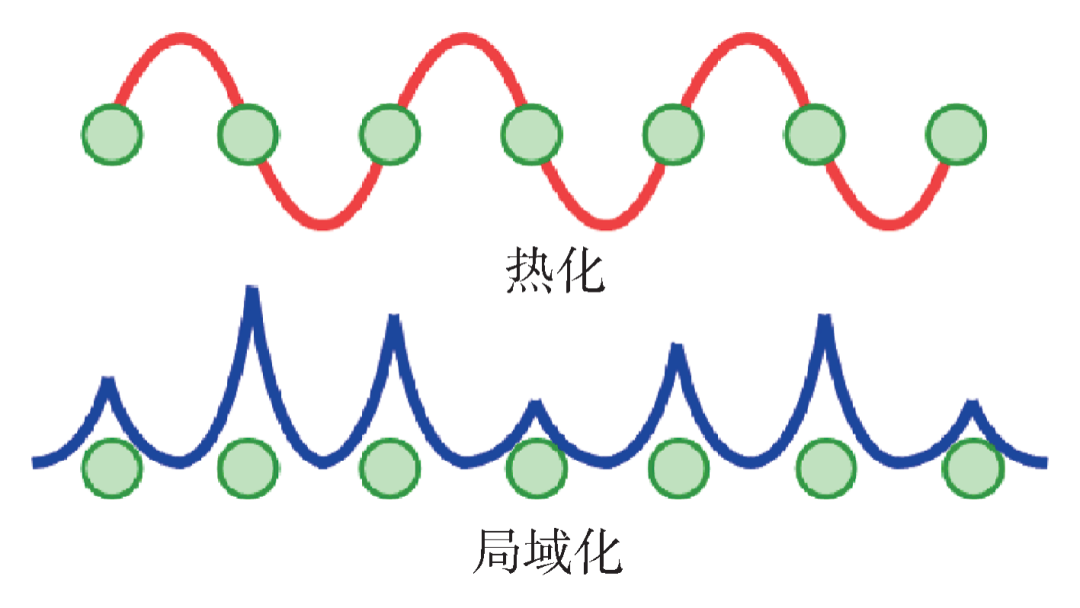
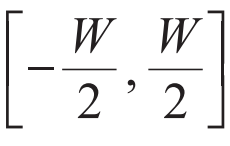 ,若紧束缚模型的带宽是B,当W>B时,就会有无序的能级跑到能带外面形成孤立的局域能级。
,若紧束缚模型的带宽是B,当W>B时,就会有无序的能级跑到能带外面形成孤立的局域能级。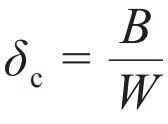 是一个临界指标,它在1以下是局域相,在1以上是热化相。
是一个临界指标,它在1以下是局域相,在1以上是热化相。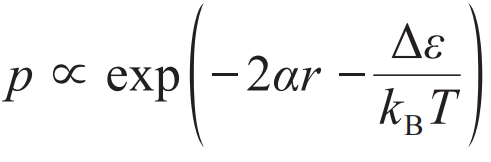 ,其中r 和Δε 分别是跃迁初末态间的空间距离和能量差,α是刻画距离无序度的参数。如果我们进一步假定无序能级的能量差与体积成反比,即Δε=cr-3,c是比例系数,则最大的跃迁概率为
,其中r 和Δε 分别是跃迁初末态间的空间距离和能量差,α是刻画距离无序度的参数。如果我们进一步假定无序能级的能量差与体积成反比,即Δε=cr-3,c是比例系数,则最大的跃迁概率为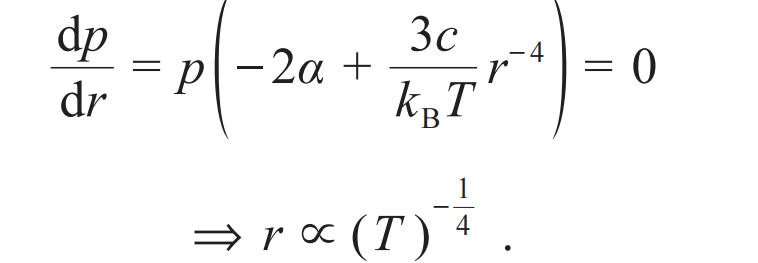
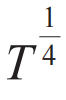 律,与实验定性吻合。
律,与实验定性吻合。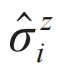 就是局域运动积分,初始状态一旦确定为它的本征态,就无法被改变。一般的,假设某个多体局域化系统的局域比特为
就是局域运动积分,初始状态一旦确定为它的本征态,就无法被改变。一般的,假设某个多体局域化系统的局域比特为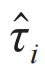 ,它的哈密顿量总可以写为如下形式:
,它的哈密顿量总可以写为如下形式: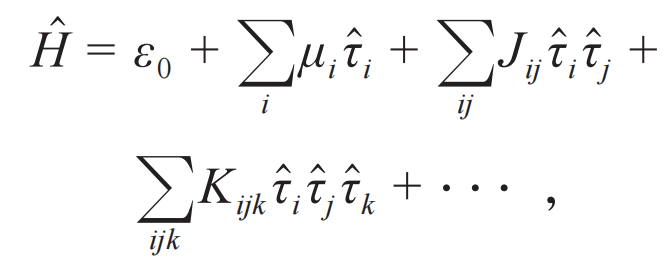
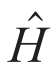 中双算符相互作用能
中双算符相互作用能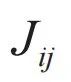 应随空间距离e指数衰减,即
应随空间距离e指数衰减,即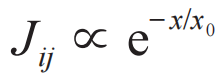 。根据测不准原理,相应的时间不确定性为
。根据测不准原理,相应的时间不确定性为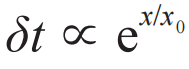 ,也就是距离越远,两个局域比特退相干的时间越长。若假定纠缠熵在x范围内各态历经、均匀分布,即S∝x,立即得到S ∝ ln δt,正是纠缠熵的对数传播律。
,也就是距离越远,两个局域比特退相干的时间越长。若假定纠缠熵在x范围内各态历经、均匀分布,即S∝x,立即得到S ∝ ln δt,正是纠缠熵的对数传播律。
6. 量子热机
6. 量子热机
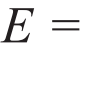
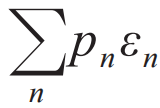 ,其中pn和εn分别是第n个本征态上的布居数和本征能量。两边求微分,立即得到:
,其中pn和εn分别是第n个本征态上的布居数和本征能量。两边求微分,立即得到: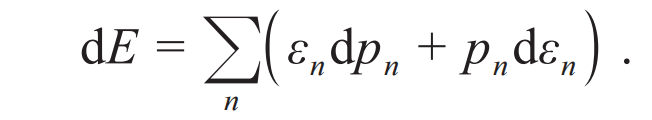
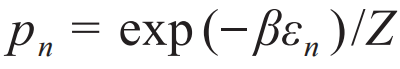 ,易得:
,易得: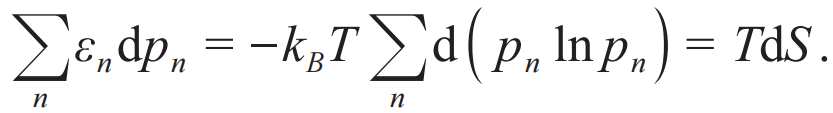
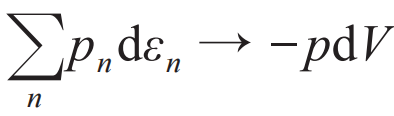 ,形式上就与第一定律一致了。
,形式上就与第一定律一致了。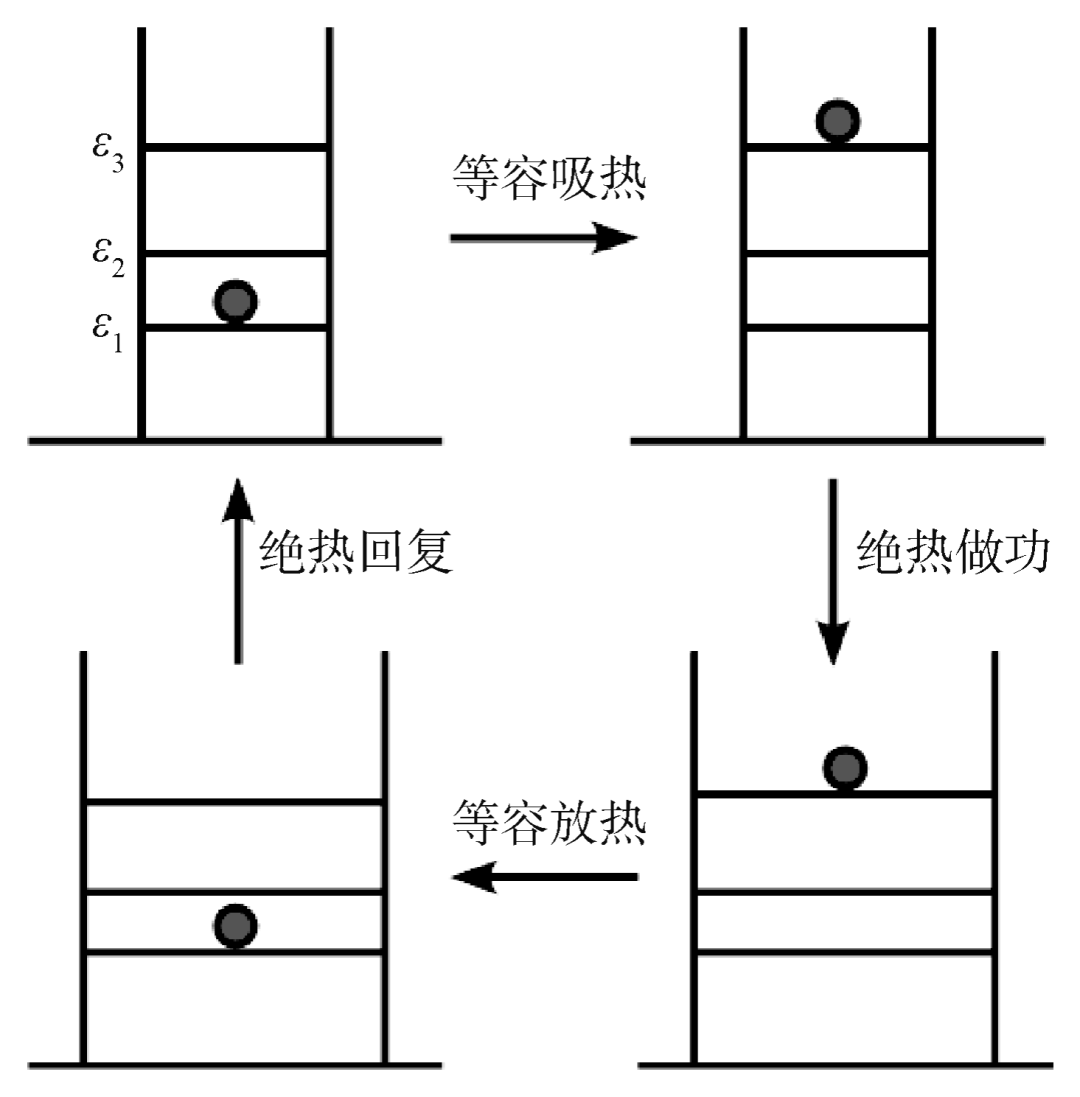
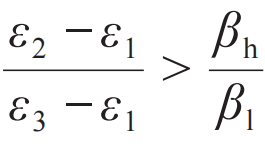 ,形式上与卡诺效率类似。
,形式上与卡诺效率类似。
7. 量子资源论
7. 量子资源论
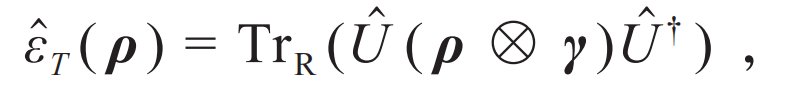
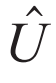 是幺正操作,且初末时刻满足
是幺正操作,且初末时刻满足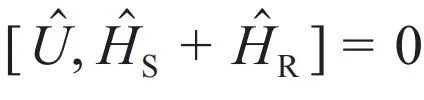 。这个超算符称为热操作 (thermal operation),它只包含量子力学中定义最良好的幺正变换和求迹操作,可以在实际物理体系中实现。热操作是完全正定保迹映射,它满足时间平移不变性并保持热平衡状态不变,这正是热力学第一和第二定律。
。这个超算符称为热操作 (thermal operation),它只包含量子力学中定义最良好的幺正变换和求迹操作,可以在实际物理体系中实现。热操作是完全正定保迹映射,它满足时间平移不变性并保持热平衡状态不变,这正是热力学第一和第二定律。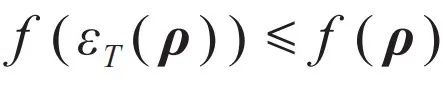 ,其中f是任意可能的函数,则热操作就是一个单向操作,它在量子热力学的框架下重新定义自然演化方向。在量子资源论中用得最为广泛的函数是迹范数和相对熵。迹范数是指
,其中f是任意可能的函数,则热操作就是一个单向操作,它在量子热力学的框架下重新定义自然演化方向。在量子资源论中用得最为广泛的函数是迹范数和相对熵。迹范数是指 ,它是一个在完全正定保迹映射下单调下降的函数。相对熵则是指
,它是一个在完全正定保迹映射下单调下降的函数。相对熵则是指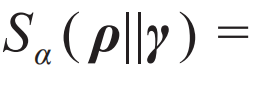
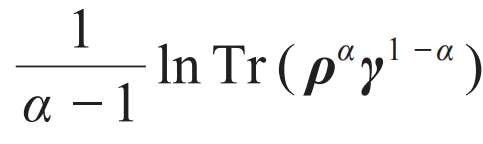 ,也叫量子Rényi相对熵,其中α代表熵的阶数,当0≤α≤2时,它是单调下降的。与标准的Rényi熵一样,当α→1时就是冯·诺伊曼相对熵
,也叫量子Rényi相对熵,其中α代表熵的阶数,当0≤α≤2时,它是单调下降的。与标准的Rényi熵一样,当α→1时就是冯·诺伊曼相对熵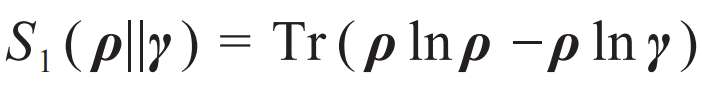 ,它反映两个密度矩阵之间的差异。
,它反映两个密度矩阵之间的差异。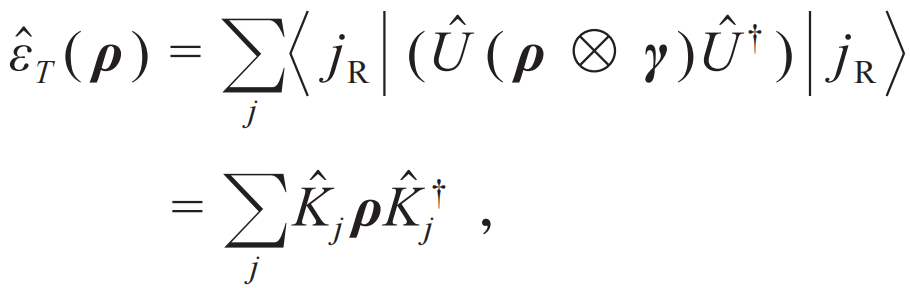
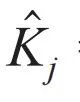 是环境部分随时间演化后再被求迹所产生的对系统的操作,称为Kraus算符。不失一般性,
是环境部分随时间演化后再被求迹所产生的对系统的操作,称为Kraus算符。不失一般性,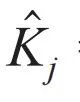 总可以分为两部分,即
总可以分为两部分,即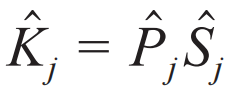 ,其中
,其中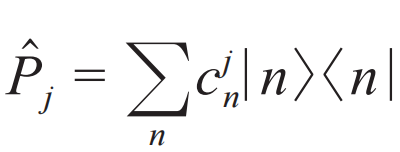 是投影算符,改变系统在不同能量本征态上的分布,
是投影算符,改变系统在不同能量本征态上的分布,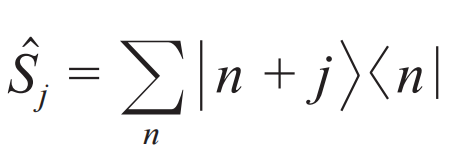 称为滑移算符,相当于把系统的所有状态向某个能量方向移动。很显然,滑移算符由环境的某个能量状态提供或是吸收了系统的能量所导致,
称为滑移算符,相当于把系统的所有状态向某个能量方向移动。很显然,滑移算符由环境的某个能量状态提供或是吸收了系统的能量所导致,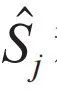 和
和 联合作用可以保持环境的状态不变,所以在这个操作下环境是一个催化剂。
联合作用可以保持环境的状态不变,所以在这个操作下环境是一个催化剂。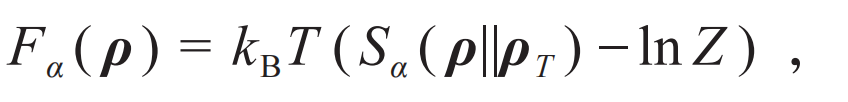
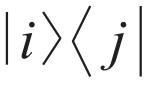 这样的在某个对称表象下的非对角元,也就是叠加态。最常见的当然就是时间平移不变性所对应的能量表象,对角元在时间演化算符作用下完全保持不变,所以叫对称态,对称态可以是纯态也可以是混态。而非对角元在时间演化时会增加一个相位,所以是破坏平移不变性的非对称态。根据热操作的单调性可以发现,最均匀的叠加态通常只能作为热操作的初态,而很难作为末态。这种难以被热操作自然演化而制备得到的非对称态,就是“昂贵的”资源,与之相反,不均匀的叠加态则是“廉价的”,能量本征态则是“免费的”。非对称性理论,可以帮助我们回答一个基础但悬而未决的量子力学问题:能量本征态的线性叠加态究竟是如何产生,又应如何被利用。此外,在非对称性理论的帮助下,我们还可以将纠缠的提纯与形成过程组成一个量子热机的循环,从而研究如何将量子相干性作为资源加以循环利用。
这样的在某个对称表象下的非对角元,也就是叠加态。最常见的当然就是时间平移不变性所对应的能量表象,对角元在时间演化算符作用下完全保持不变,所以叫对称态,对称态可以是纯态也可以是混态。而非对角元在时间演化时会增加一个相位,所以是破坏平移不变性的非对称态。根据热操作的单调性可以发现,最均匀的叠加态通常只能作为热操作的初态,而很难作为末态。这种难以被热操作自然演化而制备得到的非对称态,就是“昂贵的”资源,与之相反,不均匀的叠加态则是“廉价的”,能量本征态则是“免费的”。非对称性理论,可以帮助我们回答一个基础但悬而未决的量子力学问题:能量本征态的线性叠加态究竟是如何产生,又应如何被利用。此外,在非对称性理论的帮助下,我们还可以将纠缠的提纯与形成过程组成一个量子热机的循环,从而研究如何将量子相干性作为资源加以循环利用。
8. 通向万物理论之路
8. 通向万物理论之路
参考文献
(参考文献可上下滑动查看)
加大圣迭戈分校:量子力学

推荐阅读










