自适应控制描述了一系列技术,通过使用测量信号来改变控制行为,在不确定性条件下实现高控制性能。自适应控制的理论和实践在许多领域已经成熟。本文是《系统与控制百科全书》(Encyclopedia of Systems and Control)的“自适应控制”条目,提供了自适应控制的概述。
https://link.springer.com/referenceworkentry/10.1007/978-3-030-44184-5_110
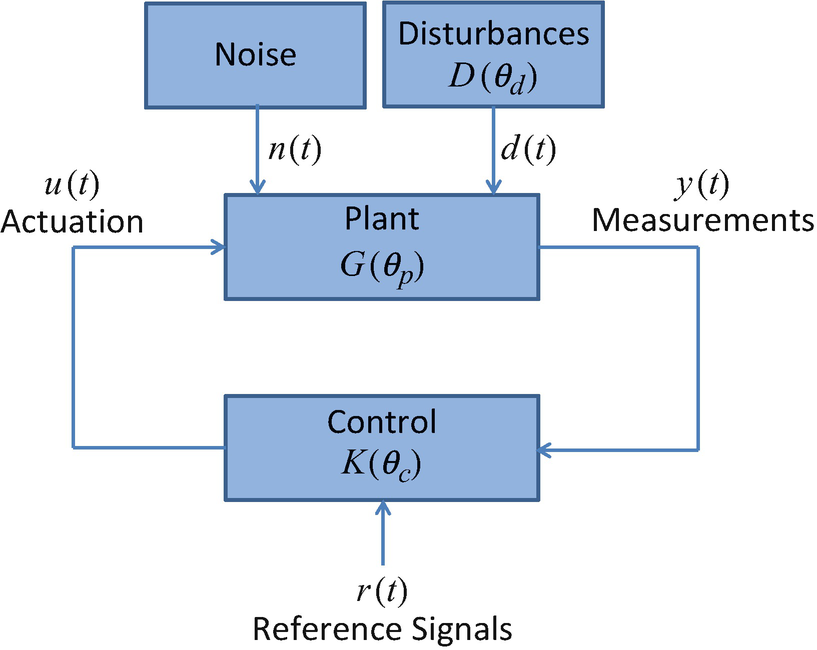
反馈控制有着悠久的历史,它使用感测、决策和执行元件来实现总体目标。控制系统的一般结构可以在图1中说明。人们早已知道,高保真度控制依赖于对被控系统的了解。例如,在大多数情况下,了解受控体(plant)增益和/或时间常数(图1中用θp 表示)对于反馈控制设计很重要。此外,干扰特性(例如,正弦干扰的频率),图1中的θd ,在反馈补偿器设计中也很重要。
许多控制设计和综合技术是基于模型的,使用模型结构和参数的先验知识。在其他情况下,使用固定的控制器结构,并且在控制系统调试期间经验性地调整控制器参数,图1中的θ。然而,如果受控体参数随时间变化幅度大或者有很大的不确定性,这些方法可能不足以实现高性能控制。
有两种主要方法来处理未知受控体和干扰特性的高性能控制:
1. 鲁棒控制(基于优化的鲁棒控制),其中控制器被设计为尽管存在不确定性,也能够适当地执行任务。变结构控制在某些情况下可能具有非常高的鲁棒性,因此是鲁棒非线性控制的一种特殊类别。
2. 自适应控制是指控制器基于测量数据学习并调整其策略。这通常采取控制器参数θ随时间变化的形式,这些参数依赖于可用数据(y(t)、u(t)和r(t))。自适应控制与智能控制(包括神经控制、最优控制和动态规划原理)有着密切联系,在其中考虑了特定类型的学习,并且也与随机自适应控制有关。
当存在大量未建模的动力学(即结构不确定性)、相对较高的噪声水平或快速且不可预测的参数变化时,鲁棒控制是最有用的。相反,对于缓慢或大部分可预测的参数变化,具有相对良好的模型结构和有限噪声水平的情况下,自适应控制可能是实现高性能控制的非常有用的工具(Åström and Wittenmark 2008)。
自适应控制的一种实用变种是控制器自动调谐。自动调谐特别适用于比例-积分-微分控制器(PID)及类似控制器,其中包括一个特定的信号注入阶段,随后进行分析、PID增益计算和实施。这些技术是分布式控制系统调试和维护的重要辅助手段。
还有许多大类的自适应控制器,它们不断监控受控体的输入输出信号以调整策略。这些调整通常由相对较少数量的系数θ进行参数化。这些方案包括直接使用可测量数据调整控制器参数的方法(也称为“隐式”,因为没有生成显式的受控体模型)。早期的例子通常包括模型参考自适应控制。其他方案(Middleto et al. 1988)显式估计受控体模型θ;之后,进行在线控制设计,因此,控制器参数θ的调整是间接的。这随后引发出一系列适用于线性系统的其他自适应控制技术(线性时不变系统的自适应控制)。
一些自适应控制算法在针对未建模的动力学、时变系统和噪声的敏感性上,存在重大问题(Ioannou and Kokotovic 1984; Rohrs et al. 1985)。这开启了一段非常活跃的研究时期,旨在分析和重新设计自适应控制以提供适当的鲁棒性(鲁棒自适应控制)(Anderson et al. 1986; Ioannou & Sun 2012)和对时变系统的参数跟踪(Kreisselmeier 1986; Middleton & Goodwin 1988)。
在这个领域的工作进一步扩展到了非参数方法,例如切换自适应控制,或监督自适应控制(Fu & Barmish 1986; Morse et al. 1992)。此外,对于非线性系统的自适应控制这个更加困难的问题,也展开了大量研究。
另一种自适应控制技术是极值搜索控制。在极值搜索(或自优化)控制中,系统的期望参考值是未知的,而我们希望在系统中最大化(或最小化)某个变量(Ariyur & Krstic 2003)。这些技术具有相当独特的操作模式,在各种应用中被证明非常重要。
迭代学习控制是一种具有非参数特性的最终控制算法(Amann et al. 1996; Moore 1993)。这种控制方案适用于具有高度结构化、重复有限运行的控制问题的系统。通过利用先前运行信息的非参数方法,在许多情况下,可以实现近乎完美的渐近跟踪。
自适应控制拥有悠久的历史,并已成为某些类型控制问题的重要工具。
线性时不变系统的自适应控制
https://doi.org/10.1007/978-3-030-44184-5_111
自动调谐
https://doi.org/10.1007/978-3-030-44184-5_113
极值搜索控制
https://doi.org/10.1007/978-3-030-44184-5_114
自适应控制历史
https://doi.org/10.1007/978-3-030-44184-5_120
迭代学习控制
https://doi.org/10.1007/978-3-030-44184-5_115
模型参考自适应控制
https://doi.org/10.1007/978-3-030-44184-5_116
非线性自适应控制
https://doi.org/10.1007/978-3-030-44184-5_117
最优控制与动态规划原理
https://doi.org/10.1007/978-3-030-44184-5_209
基于优化的鲁棒控制
https://doi.org/10.1007/978-3-030-44184-5_159
鲁棒自适应控制
https://doi.org/10.1007/978-3-030-44184-5_118
随机自适应控制
https://doi.org/10.1007/978-3-030-44184-5_231
切换自适应控制
https://doi.org/10.1007/978-3-030-44184-5_119
Amann N, Owens DH, Rogers E (1996) Iterative learning control using optimal feedback and feedforward actions. Int J Control 65(2):277–293
Anderson BDO, Bitmead RR, Johnson CR, Kokotovic PV, Kosut RL, Mareels IMY, Praly L, Riedle BD (1986) Stability of adaptive systems: passivity and averaging analysis. MIT, Cambridge
Ariyur KB, Krstic M (2003) Real-time optimization by extremum-seeking control. Wiley, New Jersey
Åström KJ, Wittenmark B (2008) Adaptive control. Courier Dover Publications, Mineola
Fu M, Barmish BR (1986) Adaptive stabilization of linear systems via switching control. IEEE Trans Autom Control 31(12):1097–1103
Ioannou PA, Kokotovic PV (1984) Instability analysis and improvement of robustness of adaptive control. Automatica 20(5):583–594
Ioannou PA, Sun J (2012) Robust adaptive control. Dover Publications, Mineola/New York
Kreisselmeier G (1986) Adaptive control of a class of slowly time-varying plants. Syst Control Lett 8(2):97–103
Middleton RH, Goodwin GC (1988) Adaptive control of time-varying linear systems. IEEE Trans Autom Control 33(2):150–155
Middleton RH, Goodwin GC, Hill DJ, Mayne DQ (1988) Design issues in adaptive control. IEEE Trans Autom Control 33(1):50–58
Moore KL (1993) Iterative learning control for deterministic systems. Advances in industrial control series. Springer, London/New York
Morse AS, Mayne DQ, Goodwin GC (1992) Applications of hysteresis switching in parameter adaptive control. IEEE Trans Autom Control 37(9):1343–1354
Rohrs C, Valavani L, Athans M, Stein G (1985) Robustness of continuous-time adaptive control algorithms in the presence of unmodeled dynamics. IEEE Trans Autom Control 30(9):881–889
对复杂动态系统的定量认识与科学调控,系统学与控制论是关键基础。集智学园联合中科院数学与系统科学研究院多位控制科学与工程领域专家共同开设了《控制科学前沿理论与方法》系列课程,为面向控制专业领域学生以及跨领域的学习者做深度科普,帮助学习控制论的核心思想、框架与方法。通过学习这些课程,学生将了解控制论的发展历程,掌握经典和现代控制方法,探索控制系统的美妙之处。此系列课程共计10节,从2024年4月2日起,每周二晚19:00-21:00线上上课。欢迎感兴趣的朋友报名参与!