神经网络是复杂的生物系统,其行为受到突触可塑性的影响。突触可以分为电突触(Electric Synapse)和化学突触(Chemical Synapse)。突触可塑性是指神经元之间突触连接强度的可变性,对于学习、记忆和神经功能的塑造至关重要。在集智俱乐部「计算神经科学」读书会,香港城市大学神经科学系助理教授冯志聪(Alan Fung)介绍了突触动力学,短期突触可塑性如何调节长期突触可塑性,以及关于突触竞争的研究。本文是社区成员对此次读书会分享的整理。
研究领域:计算神经科学,神经网络,突触动力学,突触可塑性,突触竞争,连续吸引子神经网络
这次的分享是关于突触动力学对神经网络的启发。需要了解长期突触可塑性,才能了解记忆的形成,但不能一直依赖长期可塑性,需要一个调节机制,而短期可塑性是个方案。短期突触可塑性可能调节长期突触可塑性。此次分享还介绍了作者最近的一篇关于突触竞争的文章,以及怎么在机器学习中实现类似的机制。
大脑如何产生电流?化学突触是两个神经元之间的连接,其中信息通过释放和接收被称为神经递质的化学物质来传递。神经递质可以与相应类型的受体结合,而这些受体包含离子通道。神经递质的结合可导致离子通道的打开,允许离子电流进出细胞,继而改变细胞的膜电位。突触还分为突触前端和突触后端,动作电位传递过来的时候,神经递质就会释放到受体,从而打开离子通道,造成去极化(depolarization),即把电位提高,或者是超极化(hyperpolarization),即把电位降低。
神经递质里,谷氨酸(glutamate)是兴奋性的,对应受体是AMPA和NMDA,可以引起钠离子进入细胞引起去极化。另外一个主要的神经递质是GABA受体,释放它的细胞通常称为抑制性细胞,因为它会打开抑制性受体让氯离子进入细胞,把细胞的电位压得更低,让它比较难去激发。
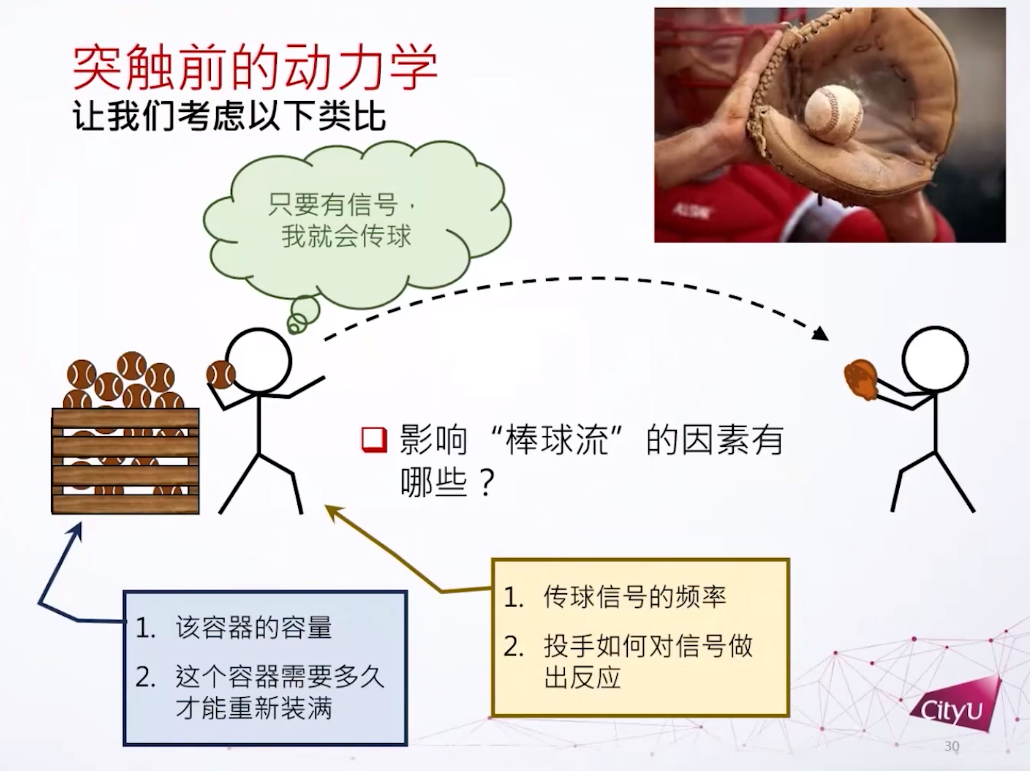
用棒球类比突触信息传递,棒球当作神经递质。这里关注的问题是,有多少库存的棒球?每次投两个还是三个?如果棒球用光了要多长时间可以重新装满?
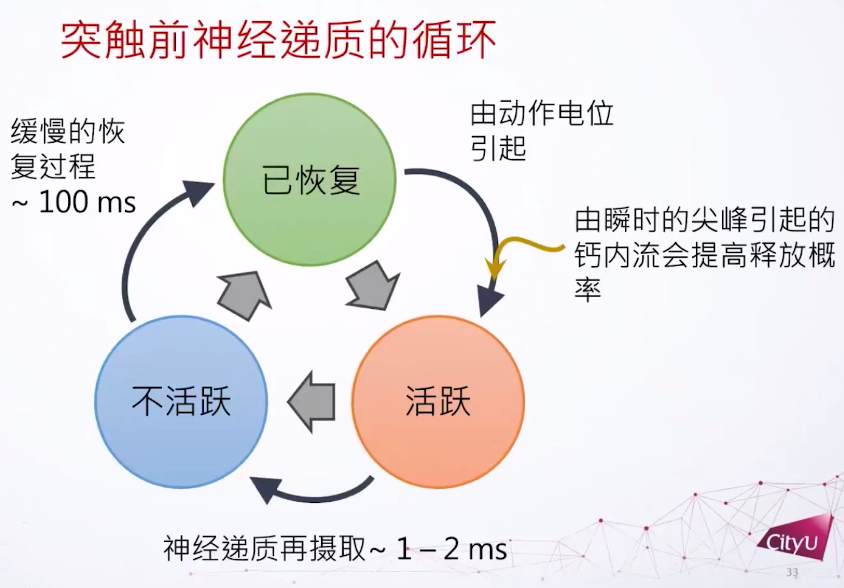
在实验中也观察到类似现象,连续的突触激发会导致突触电流的下降。神经递质发出后还有个回收的过程,神经递质不能在突触前和突触后之间存在太久,不然受体会受到过分刺激。所以只需要一瞬间打开,一两个毫秒之后就回收。神经递质定义了三个主要的态:已恢复,活跃,不活跃,它们形成一个循环。如果很久没有动作电位引起神经递质激发,就成为活跃,激发后1到2个毫秒后转为不活跃。在这个过程之后有一个比较慢的恢复过程,大概100毫秒,然后可以再激发。每次激发可以有一些钙离子的内流,可以提高释放的概率。基本上这个循环就是形容神经递质的动力学。
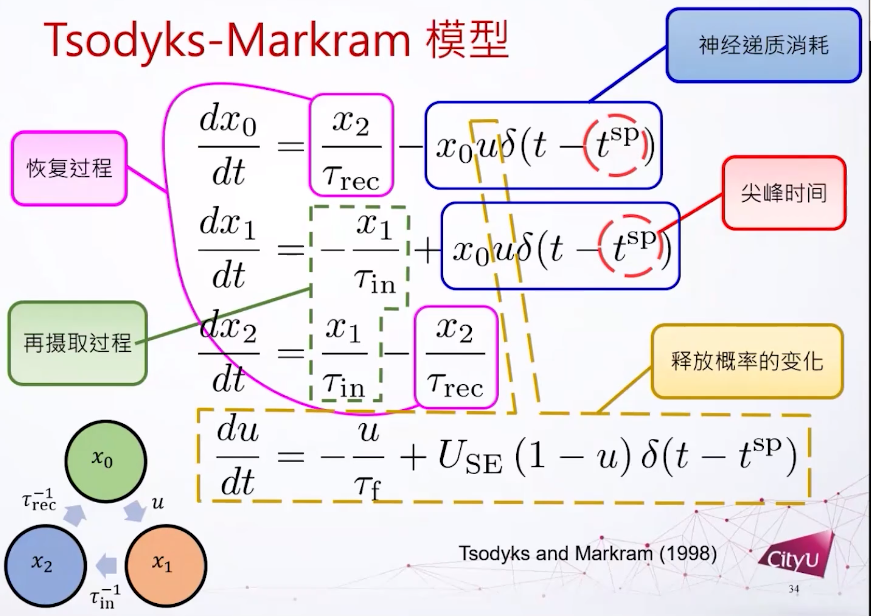
下图是突触的Tsodyks-Markram模型,下面图中框起来的6个项加起来就是0。如果我们把前三个微分方程加起来也是0,代表x0加x1加x2是一个常数。所以这里假设神经递质的总数量是一个常数。
突触的Tsodyks-Markram模型
Neural Networks with Dynamic Synapses. Misha Tsodyks, Klaus Pawelzik, Henry Markram. Neural Computation (1998).
然而,短期突触可塑性对连续吸引子网络(CANN)有什么启示呢?在上世纪70年代,日本理化学研究所的甘利俊一教授已经开始提出用二元神经元(binary neuron)去模拟连续吸引子。
神经科学教科书里面一个比较著名的实验,猴子被训练在桌子上对不同方向做反应,做反应的运动皮层(motor cortex)要做一些编码去计划它的下一个动作。发现细胞发放率和计划的方向有关联,是一个调谐曲线,说明神经细胞有一个特定方向的偏好。
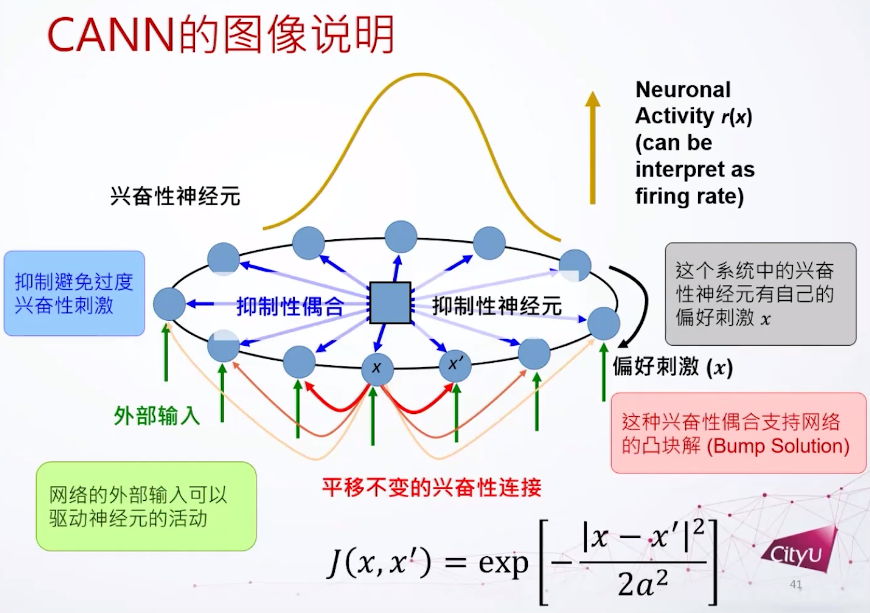
如何建模呢,假设每个细胞有自己的偏好,我们把细胞根据偏好放在环里面。兴奋性连接用高斯函数给出,还定义了抑制性的耦合和神经元,这些东西加起来可以支持一个凸块解(bump solution)。这个网络就是有了平移不变的兴奋性连接,加上一个抑制性的偶合,再加上一些外部连接,然后就可以支持这个凸块解。
我们再看连续吸引子网络的动力学。首先有个变量u,有两个参数x和t,Relaxation 项表示衰减,还有所有权重的加和,以及外部输入。
Computing with Continuous Attractors: Stability and Online Aspects. Si Wu, Shun-ichi Amari. Neural Computation
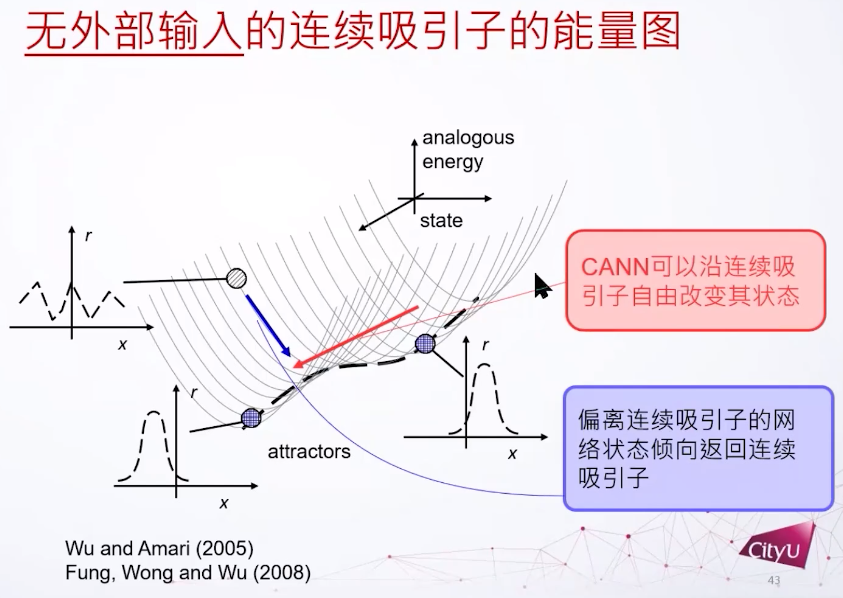
下图标出了两个稳定的态,对应的是凸块解这个解的不同位置。连续吸引子每一点都是吸引子,这个系统的态可以跑来跑去,如果偏离了这个连续吸引子的底部就会被吸回。
Dynamics of neural networks with continuous attractors. CC Alan Fung, KY Michael Wong, Si Wu. Europhysics letters.
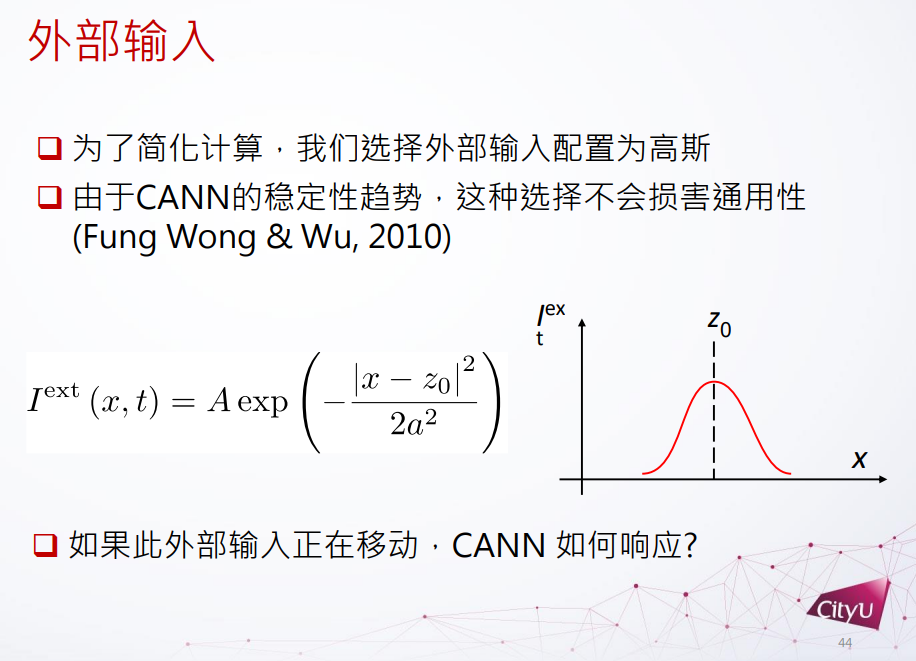
外部的输入可以有很多不同的可能性,这里简化分析外部函数为高斯函数。研究发现给高斯函数输入时连续吸引子一般不会被破坏,但是如果外部输入函数在移动,连续吸引子网络怎么反应?
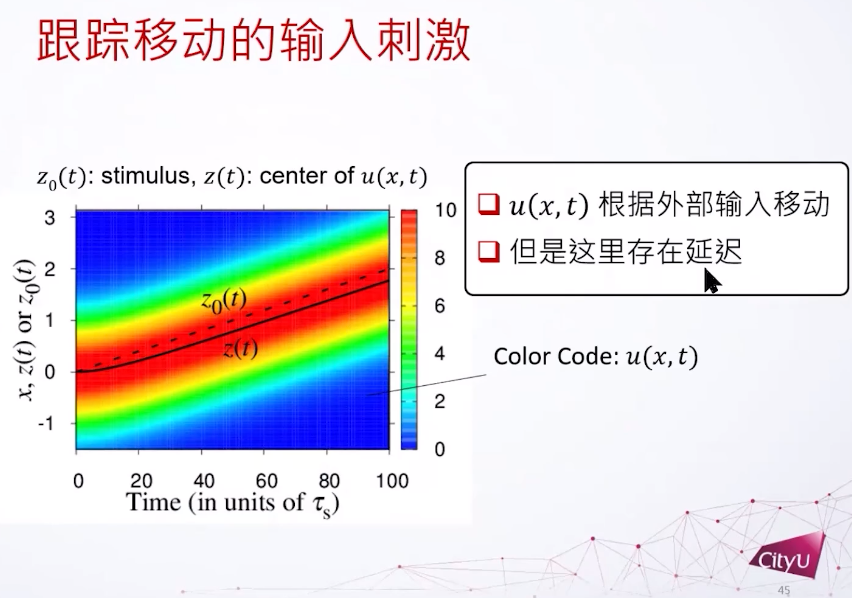
Z0是外部输入的位置,纵轴是不同输入的位置,横轴是时间。发现u会根据外部输入移动,并且有延迟。但是在大脑中,如果延迟累加以后,很可能就不能做即时的反应。
然后我们先把短期的突触动力学放进去,短期突触动力学有两个部分,一个部分是短程抑制(short term depression,STD),另外一个就是短程增强 (short term facilitation,STF)。现在我们再把这个短期的衰减放进这个方程里面,本来没有p这一项,p模拟突触抑制。p这个函数会倾向于回到1这个状态,会被神经激发减小,所以结果就是如果这个神经细胞被激发,p会下降。而如果神经的活动没有减少,p会回到1。而这个τ_d这个数字它的意义就跟神经递质恢复的时间差不多,β和释放的概率差不多。这个模型和Tsodyks-Markram模型是差不多的。
Delay compensation with dynamical synapses. Chi Fung, K Wong, Si Wu. Advances in Neural Information Processing Systems.
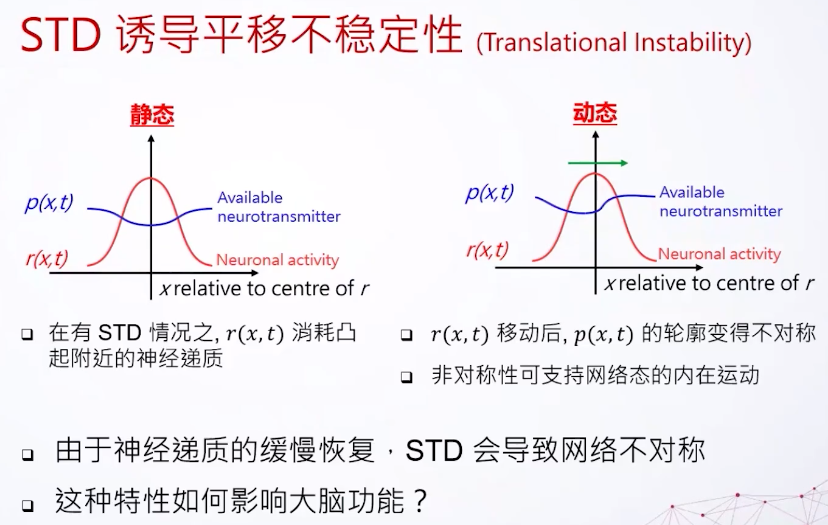
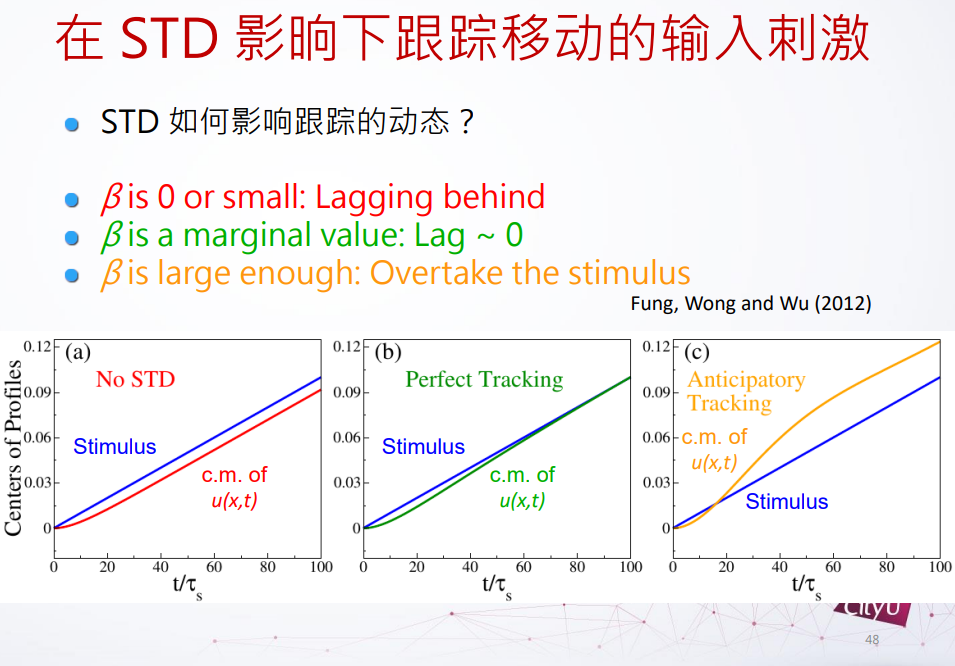
最后我们看看这个东西会怎么影响连续吸引子网络,我们只需要看它的动态跟静态。静态,比方说我们现在有一个神经的激发,他们拥有的可以激发的神经递质会减少。因为神经递质还来不及恢复,所以我们看到这里的曲线会比较小一点。动态的就不一样了,因为想象一下如果这东西在这里跑,其实是可以用到比较新的还没被完全激发的细胞,所以这里的神经递质会多一点。但是这里好像有一个尾巴,因为这是以前在上一个瞬间神经细胞活跃的区域,所以看到是变成不对称的样子。其实这是连续支持网络的动态,所以我们如果把短期的衰减加上连续吸引子网络,会有一种不稳定性,我们叫它平移不稳定性(translational instability)。是一个内在的动态,原因就是神经递质的缓慢恢复,但是这个东西怎么影响我们大脑?其实可以用来做延迟的补偿。
在没有短期抑制的时候,u在网络的态是落后外部刺激的,但是如果我们增加β,短期抑制力度的时候,发现延迟减少,如果再增加多一点点的时候,这个网络的态跑到移动的外部刺激的未来位置,这个东西叫它做预期跟踪(anticipatory tracking),是抵消延迟的一种可能的方案。
但是这个预期跟踪是不是真的存在?其实在我们大脑里面真的有这个。在1998年,在大鼠里面看到一些头部方向细胞指向的不是现在的头部位置,而是未来的头部位置。他们在实验当中把老鼠固定在可以转动的板子上面,之后他们转动老鼠,观察头部方向细胞的激发。现在就可以控制预期,因为得知道速率的快慢。预期性跟踪可以解释和实验上差不多的时间尺度。
Modeling Attractor Deformation in the Rodent Head-Direction System. Jeremy P. Goodridge and David S. Touretzky. Journal of Neurophysiology.
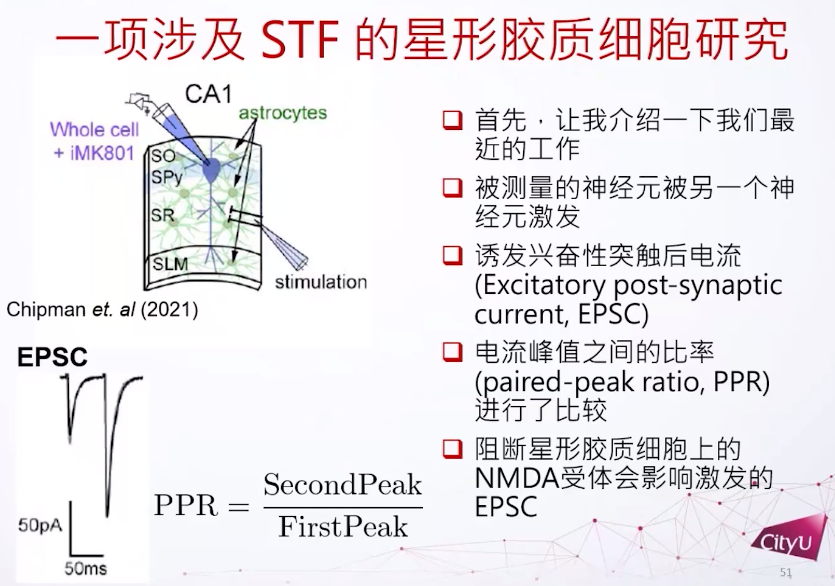
那么短期的突触可塑性和长期的突触可塑性有什么调节的关系呢?这涉及到之前的一个工作,跟星形胶质细胞有关,它是细胞旁边的胶质细胞,但是它的形状是星形的。这里有个皮层组织的切片,里面包含星形细胞和其他的神经细胞。但不是直接激发了CA1锥体细胞,而是激发另外的细胞,再间接激发CA1锥体细胞。因为想看如果影响了星形细胞的活动,这个被激发的细胞有什么影响,所以这里关注的是一个比较新的领域,就是看星形胶质细胞上面 NMDA 受体对突触后或突触前的细胞有什么影响。最主要的方法是看它的两个尖峰,因为他们每一次激发都会在突触后神经元有个尖峰。而这两个峰值的比例——PPR,是用来衡量神经元的短期可塑性有什么变化。
PPR是用衡量它的短期可塑性有多强的指标。比方说在这里看到第一个激发跟第二个激发其实有明显的差别,第二个激发比较强一点,所以这两个细胞是做了短期增强。如果在星形胶质细胞上再加一些NMDA受体的阻断就发现PPR比例的方差会减小,用不同的NMDA受体也是达到同样的结果。
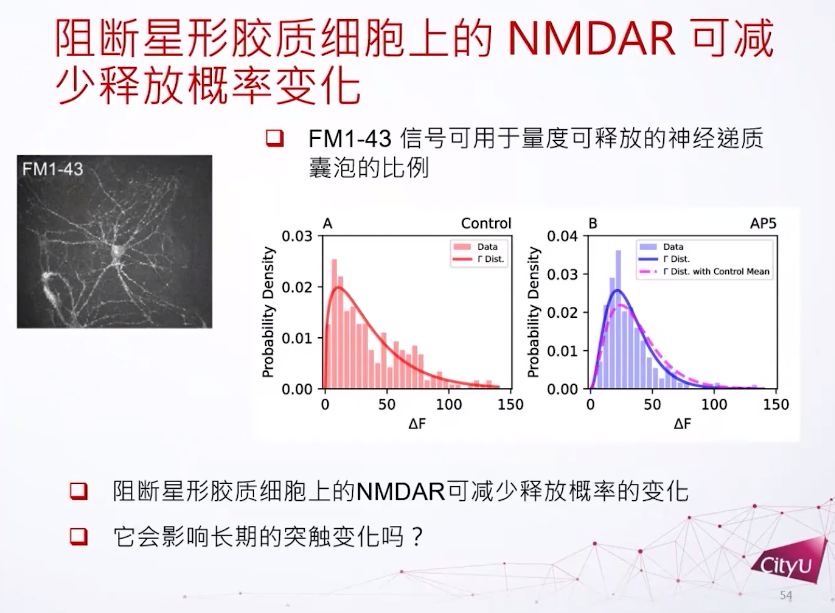
如果我们阻断NMDA受体,在突触前其实也观察到激发概率的变化。神经递质的释放概率其实是一个伽玛分布,没有被阻断情况下,激发概率更偏向于0但是会比较长尾一点。但是如果NMDA受体被阻断,比较小的激发概率会上升,但是比较高的激发概率会减少很多。简单来说就是平均没有大的改变,但是释放概率会改变很多。
我们现在知道星形胶质细胞会影响突触后STF的变化,也会影响突触前神经递质释放概率的变化。
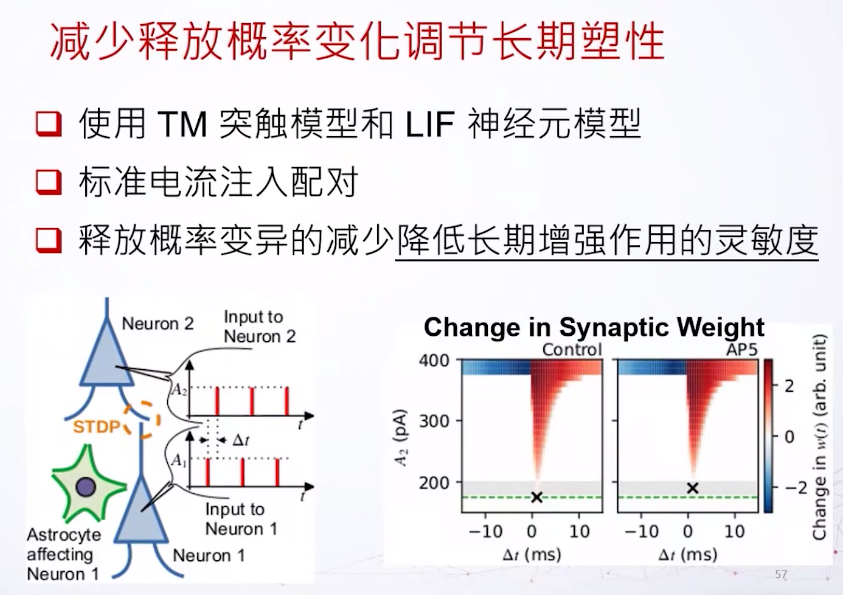
想象我们现在有两个细胞,一个突触前一个突触后。如果他的动作电位的时间有一个时间差,他们之间的耦合就会有一个变化,我们叫它突触权重,突触权重的变化是基于这个时间差到底有多大,或者是正还是负。如果突触后的发放晚于突触前,这个连接会被增强,反过来就会减弱。由于这个改变的时间持续期比较长一点,所以这个变化也称为长期可塑性。
减少释放概率的变化可以调节长期突触可塑性。可以用数值模拟做出来,我们用两个LIF(leaky integrate and fire)模型,我们先把它注入一些简单的电流。还有一个时间差,让突触前电流足够大去让它激发,但是突触后神经元输入的电流有一个不同的大小,之后我们用这个大小来判断长期可塑性的敏感灵敏度。我们知道如果突触前神经元被星形胶质细胞影响的话,它的释放概率的方差会减小,以这个观察为模型的基础,在不同的激发时间差,还有不同的突触后神经元的电流输入。可以看到如果这个星形细胞的NMDA受体被阻断,突触后神经元的敏感度会降低,因为需要更大的电流才可以激发长期突触可塑性。
使用更现实一点的泊松尖峰输入,模拟里面也是发现平均来说星形细胞的NMDA受体阻断可以调控长期突触可塑性的能力。
比较小的总结:化学突触的动力学可以重塑神经元系统的行为,首先可以破坏连续吸引子网络平移的稳定性,另外会影响长期突触可塑性。
最后这个是最近的研究,突触间的竞争到底有什么用。因为在一些生物学的过程中突触其实在竞争。其中一个重要的功能就是做模式分离(pattern separation),突触的竞争提高了模式分离的能力。数据科学里经常看到不同的数据在特征空间里有重叠,在比较好的特征空间里可以把它们清晰的分开来,这是一个模式分离的过程,用简单的支持向量机就可以很好的解决。然后是成体的神经生成,这个是很大争议的问题,其实每一年都有很多人发不同文章在争论到底有没有这个事情。
比如在内嗅皮层是不是真的有神经细胞生成呢?做运动的时候,有些新细胞的反应可以观察到。不成熟的细胞在长得大一点的时候他会尝试连接不同的细胞。当成熟的时候,连接就会变得比较稳定,或者是比较有选择的连接。成熟的细胞会跟未成熟的细胞做竞争,因为成熟的细胞已经拿到连接了,新的细胞还没拿到连接,拿到稳定的位置才能继续生存下去。他们发现如果加一些药物去加强竞争,其实可以提高记忆的精度。
还没成熟细胞的突触可塑性比较强一些,在成熟之后比较弱一点。老的细胞只对一些特定的很强烈的激发有比较明显的改变。
Enhanced synaptic plasticity in newly generated granule cells of the adult hippocampus. Christoph Schmidt-Hieber, Peter Jonas & Josef Bischofberger. Nature.
他们还去干扰新的细胞的生成,看这个还能不能分开互相干扰的记忆。当然这个能力会消失,但是这样做其实不太会伤害神经细胞,因为神经细胞还有能力去对非常不同的记忆进行区分。但如果我们没有成体神经生成,我们区别类似事物的能力会被破坏。我们关注这个问题因为这个问题对模式分离是很重要的。
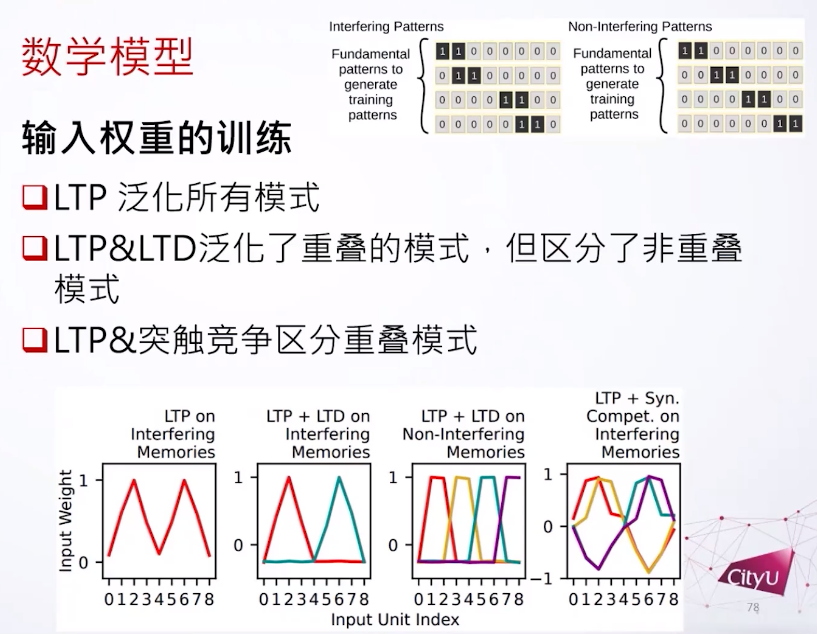
接下来做的东西有点像机器学习,首先有两种模式的数据。首先一个是干扰模式(interfering patterns),模拟一些很类似的记忆,模式之间有重叠。另外一个不干扰的模式(non interfering patterns)就是记忆之间没有关系。这个是我们用来训练的基本模式数据,再加上一个随机向量,然后生成的。他们分别训练,用来模拟不同的场景。
Competition on presynaptic resources enhances the discrimination of interfering memories. Chi Chung Alan Fung, Tomoki Fukai. PNAS Nexus 2023.
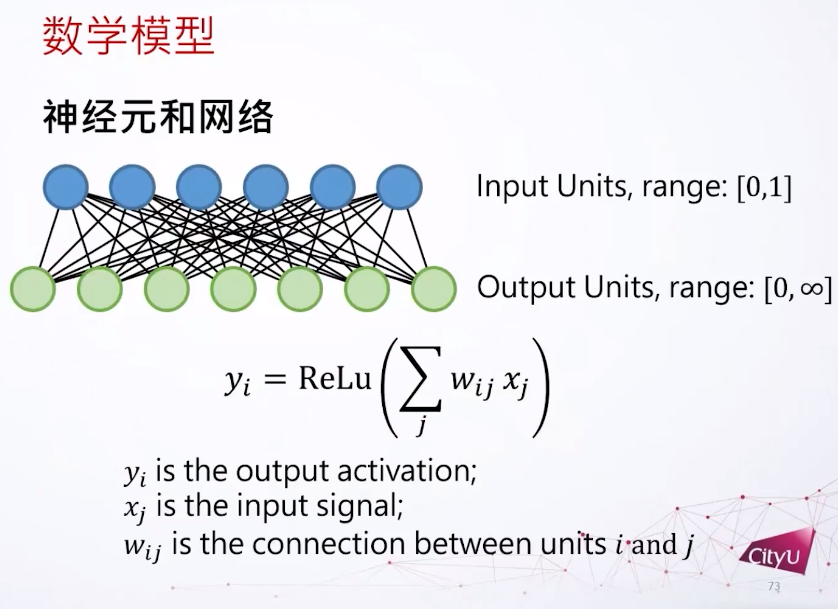
输入单元是0-10的数字。我们现在要学的就是到底什么样的权重帮可以模式识别。
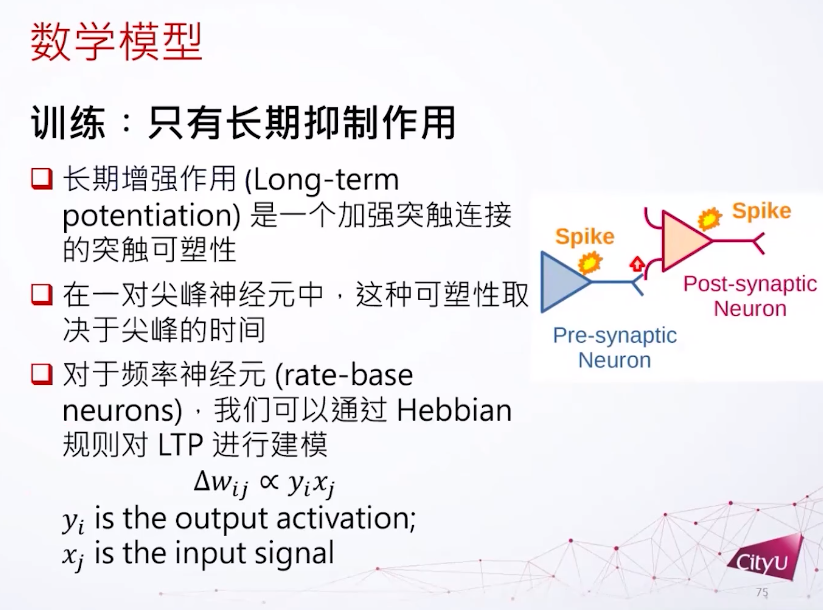
我们现在是模拟的不是尖峰神经元,用的是基于发放频率的神经元,所以我们用赫布学习来模拟LTP。
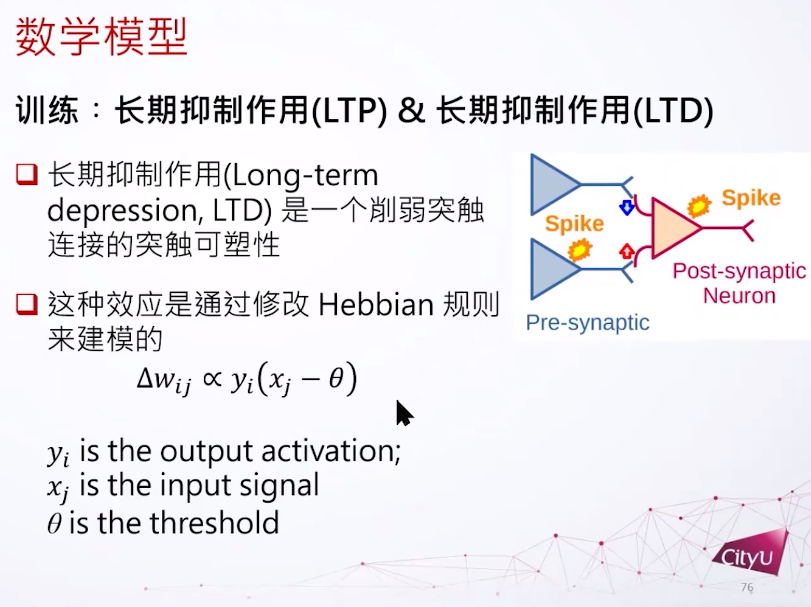
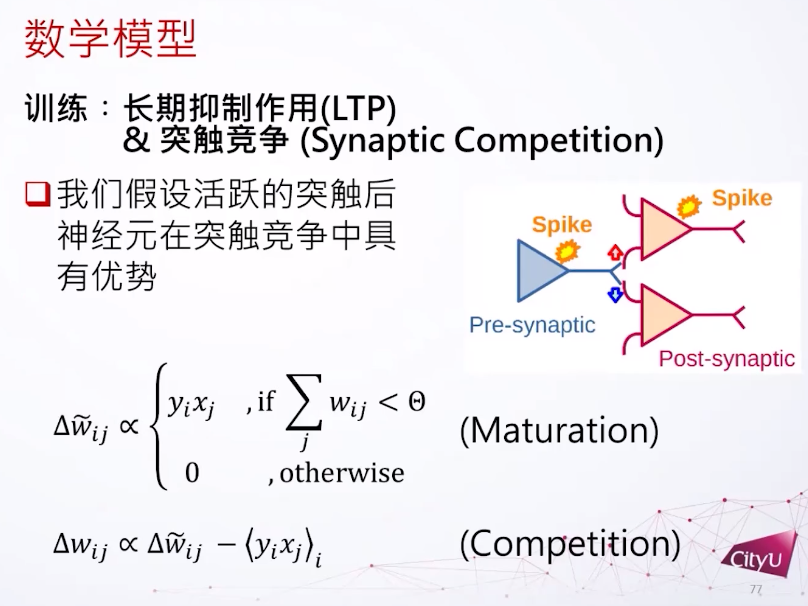
如果我们用LTP来训练,我们发现神经细胞会对所有的模式都有反应,我们说它泛化了所有的模式。如果LTP加LTD,看到神经细胞分成两组,但是它还是不能分别重叠的模式。但是LTP加上突触竞争,很奇怪的是他们可以区别所有模式了。
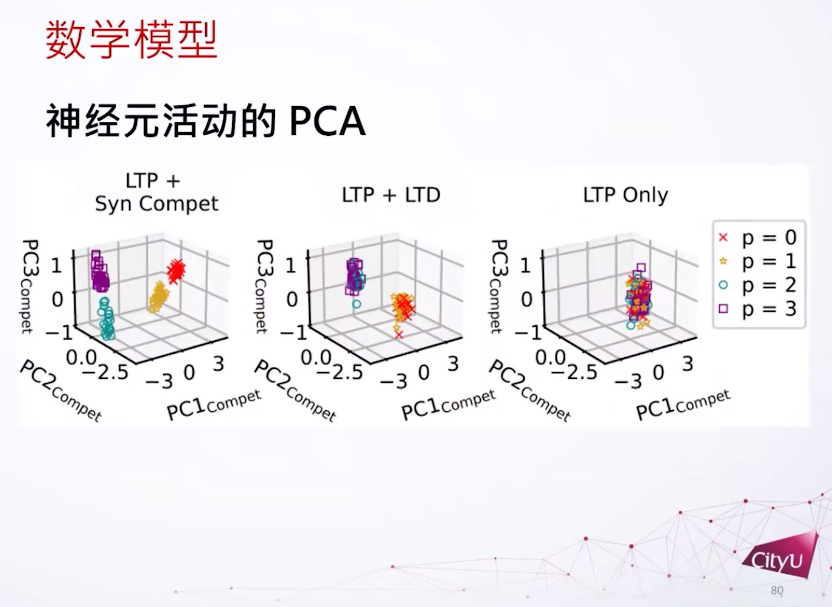
把这个输入权重用PCA分类。如果我们只看这个LTP,所有特征都会重叠,因为倾向于把所有东西都泛化,但是LTP加上突触竞争可以分离所有模式。
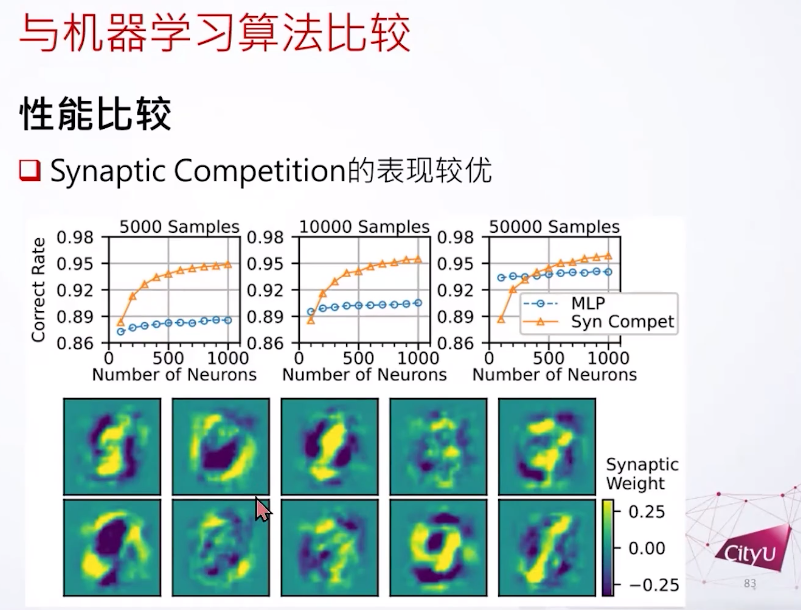
之后我们在MNIST数据集里测试。我们发现如果用很少的样例,还有短一些的训练时间,突触竞争是可以做到比较好的结果。比如突触竞争只学了一次,但结果是让人意外的好。学一次就能泛化出这些很奇怪的输入权重,好像是把溶解的数字放进他们的输入权重,或者是自动把这个突触竞争搞成一个特征,把不同特征放在不同的神经元一样。
这个是第二个总结就是这是基于竞争的学习规则,来自成体神经生成,但在我们的不同场景。比较少资源的时候其实这个这个突触竞争比反向传播要好一点。很奇怪的是这个输入的权重会看起来像溶解的数字一样,好像把不同特征分叉开来。在这个应用上我们看到突触竞争可以支持模式分离。
冯志聪(Alan Fung),2006 年开始研究连续吸引子神经网络(CANN)模型。
研究方向:专注在计算神经科学领域,基于数学工具和数值方法的基础脑科学的计算模型、神经现象的机器学习实现、数据驱动的神经数据分析,希望能够促进神经科学和人工智能的相互启发。
人类大脑是一个由数以百亿计的神经元相互连接所构成的复杂系统,被认为是「已知宇宙中最复杂的物体」。本着促进来自神经科学、系统科学、信息科学、物理学、数学以及计算机科学等不同领域,对脑科学、类脑智能与计算、人工智能感兴趣的学术工作者的交流与合作,集智俱乐部联合国内外多所知名高校的专家学者发起神经、认知、智能系列读书会第三季——「计算神经科学」读书会,涵盖复杂神经动力学、神经元建模与计算、跨尺度神经动力学、计算神经科学与AI的融合四大模块,并希望探讨计算神经科学对类脑智能和人工智能的启发。读书会从2024年2月22日开始,每周四19:00-21:00进行,持续时间预计10-15周,欢迎感兴趣的朋友报名参与,深入梳理相关文献、激发跨学科的学术火花!
详情请见:计算神经科学读书会启动:从复杂神经动力学到类脑人工智能