噪声通常被认为会影响从时间序列中提取有效的动力学模型,因此传统方法通常需要减轻噪声对学习动力学的影响。另一方面,噪声有驱动稳定态之间随机转移的作用。为了从数据中捕捉和预测噪音诱导的随机转移,在最近发表于 Nature Communications 的一项研究中,来自电子科技大学和北京师范大学的研究者首先尝试应用当下流行的机器学习方法 SINDy、FORCE,但发现即使对于最简单的白噪音双稳态系统这些方法也不准确。因此,作者推广了另一类机器学习模型——储备池计算,并通过重点关注一个控制时间尺度的超参数,设计了可以学习随机转移的新方法。这种方法在一系列例子中展现出良好效果,比如对蛋白质折叠的实验,从仅含有几次状态转移的数据中便能学习到准确的转变动力学。这项研究表明预测噪声诱导的现象还有广泛的探索空间,需要系统地推广主流的机器学习方法。
研究领域:机器学习,储备池计算,转变动力学,噪声诱导转变
林泽群 | 作者

论文题目:Learning noise-induced transitions by multi-scaling reservoir computing
https://www.nature.com/articles/s41467-024-50905-w
噪声诱导的转变在自然界中普遍存在,并且发生在具有多稳态的各种系统中。例如,电路中不同电压和电流状态之间的切换、噪声驱动的基因开关、噪声诱导的早期生命自我复制体的生物手性、蛋白质折叠态转变[1]、以及具有多稳态概率分布的化学反应。学习噪声诱导的转变对于理解这些系统的关键现象至关重要。在许多情况下,只有时间序列可用,而事先并不知道数学方程。为了有效地从时间序列中学习和预测噪声诱导的转变,有必要区分慢时间尺度和快时间尺度:在不同稳定状态周围的快速弛豫和它们之间的慢速转变,其中快速时间尺度的信号通常被视为噪声。因此,从时间序列中学习随机转移仍然是一个难题。
近年来,有许多机器学习方法致力于从数据中学习动力学。一种方法使用稀疏识别非线性动力学(SINDy)来识别非线性动力学、对时间序列数据去噪并从数据中参数化噪声概率分布。由于优化问题的非凸性,该方法可能难以稳健地处理大型函数库的回归。另一类方法则采用物理启发神经网络进行数据驱动的偏微分方程求解和发现,或从数据中提取Koopman特征函数。然而,这些方法需要大量的数据来训练深度神经网络,并对网络进行精细调整。
此外尽管上述方法具有广泛的应用,但它们尚未被用于研究噪声诱导的转变。为了学习噪声诱导的转变,作者首先利用SINDy [2, 3] 和循环神经网络 (RNN) [4] 对含有噪声的数据进行处理。作者发现,即使在具有高斯白噪声的一维双稳系统中,SINDy和RNN也无法准确预测随机转移。作者还对数据应用了滤波器 [5, 6],获得平滑的时间序列,然后使用SINDy 处理滤波后的数据,但这种方法仍未能准确捕捉噪声诱导的转变。同样,First-Order, Reduced, and Controlled Error (FORCE) 学习方法 [7],包括其各种版本如full-FORCE和尖峰神经元模型 [8],在实验数据中也未能完全捕捉随机转移,并且需要相对较高的计算成本。这些尝试表明,这些传统方法主要设计用于对噪声数据进行去噪,以学习确定性动力学,而非捕捉噪声诱导的现象。因此,需要开发一种新方法来预测随机转移。
作者注意到一种机器学习架构——储备池计算 (RC) [9-11] 可能适合这一任务。储备池计算的训练只需要线性回归,这比需要反向传播的神经网络在计算上更为快速。研究发现,储备池计算在学习动力系统方面效果显著,包括混沌系统。此前曾有一个工作尝试使用RC来处理噪声诱导的转变 [12],但依赖于事先知道确定性动力学方程的假设,这在实际问题中过强。实际上,确定性动力学的先验知识往往缺乏,有时甚至无法通过方程直接描述。那么能否仅基于数据,在没有任何确定性方程的先验知识的情况下预测噪声诱导的转变呢?
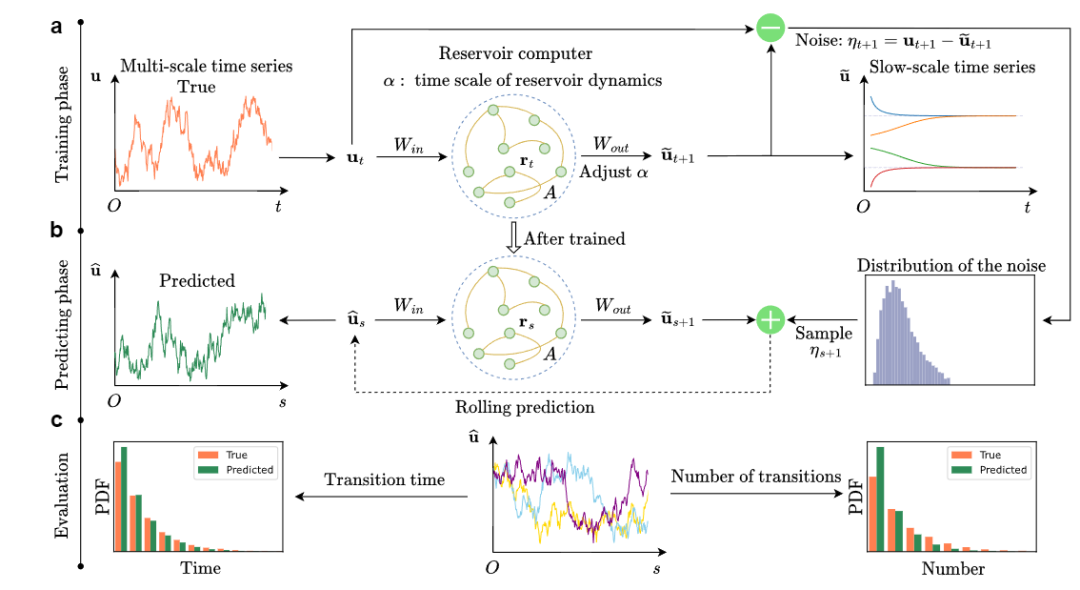
图1:多尺度化储备池计算的框架。(a) 快慢尺度混合的随机时间序列,其中快尺度的部分可以被视为噪声,导致稳定状态之间的噪声诱导转换。在训练阶段,输出矩阵Wout被训练。调整超参数α可以改变输出的时间尺度,适当选择的α可以使输出与慢尺度动力学相匹配。然后将快速时间尺度信号η分离为噪声时间序列或分布。(b) 在预测阶段,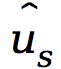 输入到训练好的储备池中以生成
输入到训练好的储备池中以生成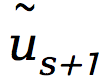 。在下一个时间步s+1,输入
。在下一个时间步s+1,输入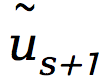 是
是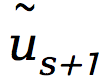 加上从分离出的噪声分布中采样的噪声ηs+1。这个过程称为滚动预测迭代进行,以生成预测时间序列
加上从分离出的噪声分布中采样的噪声ηs+1。这个过程称为滚动预测迭代进行,以生成预测时间序列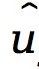 。(c) 对预测转换统计的评估。中间处
。(c) 对预测转换统计的评估。中间处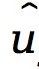 的不同颜色线条代表重复多次的预测。通过转换时间和转换次数的统计量来评估准确性。PDF:概率密度函数。
的不同颜色线条代表重复多次的预测。通过转换时间和转换次数的统计量来评估准确性。PDF:概率密度函数。
在本研究中,作者开发了一种多尺度储备池计算框架,用于在无模型的情况下学习噪声诱导的转变。该方法的灵感来自于研究发现储备池中的超参数决定了储备池动力学的时间尺度 [13]。鉴于多尺度时间序列,可以调节超参数以匹配慢时间尺度的动力学。当储备池通过拟合输出层矩阵捕捉到慢时间尺度的动力学后,可以将快时间尺度的序列分离为一个噪声分布。在预测阶段,作者利用训练好的储备池计算机来模拟慢时间尺度的动力学,然后将从分离的噪声分布中采样的噪声(对于白噪声)或从第二个储备池中学习的噪声(对于彩色噪声)加回。整个过程在时间点上迭代,称为滚动预测。值得注意的是,当前方法与之前将噪声仅视为干扰因素的方法有所不同。
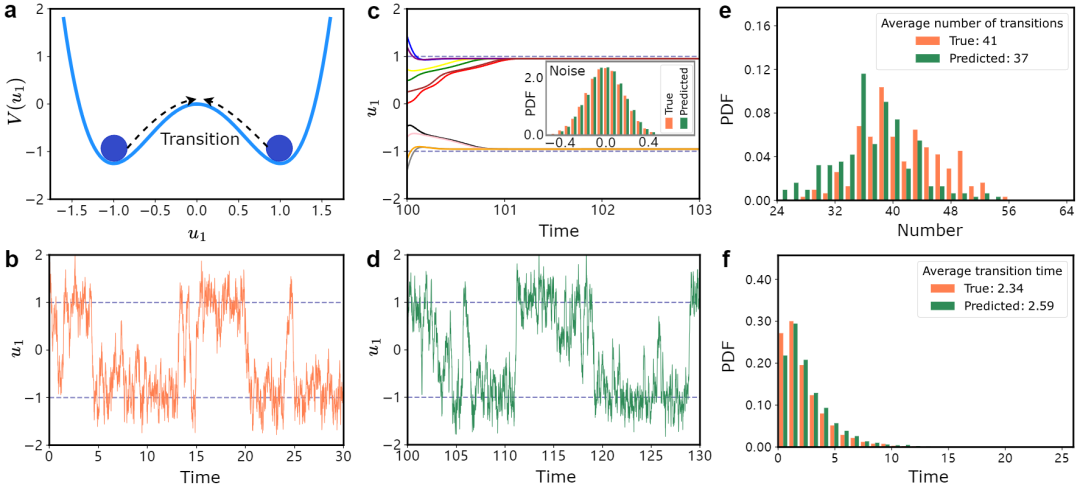
图2:从一个含白噪音的一维双稳系统中提取随机转移 (a) 含有白噪音的一维双稳系统中随机转移的示意图。(b) 从正文中Eq. (9) (b=5, c=0, ε=0.3, u1(0)=1.5, δt=0.01) 生成的训练数据,此处长为 t=30. (c) 训练得到的慢时间尺度模型将10个不同起点转换为十条不同的时间序列(彩色线)收敛到对应的稳态并且分离出噪音分布。(d) 在t∈[100, 130]的预测数据。(e) 测试和预测数据中的转移次数匹配。转移代表从u1=-1到u1=1的转换,反之亦然。预测的长度是10000δt (f) 测试和预测数据转移时间的直方图,转移时间代表两次连续转移之间的间隔。
为了证明当前方法的有效性,作者将其应用于两类场景。第一类场景的数据来自于随机微分方程 (SDE),用于测试该方法;第二类场景的数据则是实验数据 [6]。对于第一类场景中的白噪声,包含一维(1D0双稳梯度系统、二维 (2D) 双稳梯度和非梯度系统、具有倾斜势的一维和二维梯度系统、二维倾斜非梯度系统以及二维三稳系统。该方法能够捕捉转变时间的统计特征和转变次数。对于第一类场景中的彩色噪声,作者研究了具有Lorenz噪声(Lorenz-63模型和Lorenz-96模型 [12])的双稳梯度系统,能够在不假设知道动力学确定性部分的前提下准确预测特定的转变时间,这区别于 [12] 中的要求。对于第二类场景,作者将该方法应用于蛋白质折叠数据,并探索了准确训练所需的最少数据量,这有助于减少实验中对广泛测量的需求。
这里展示了该方法在部分例子中的结果,包括含白噪音的一维双稳态系统(图2)和实验上的蛋白质端到端长度数据(图3)的结果。
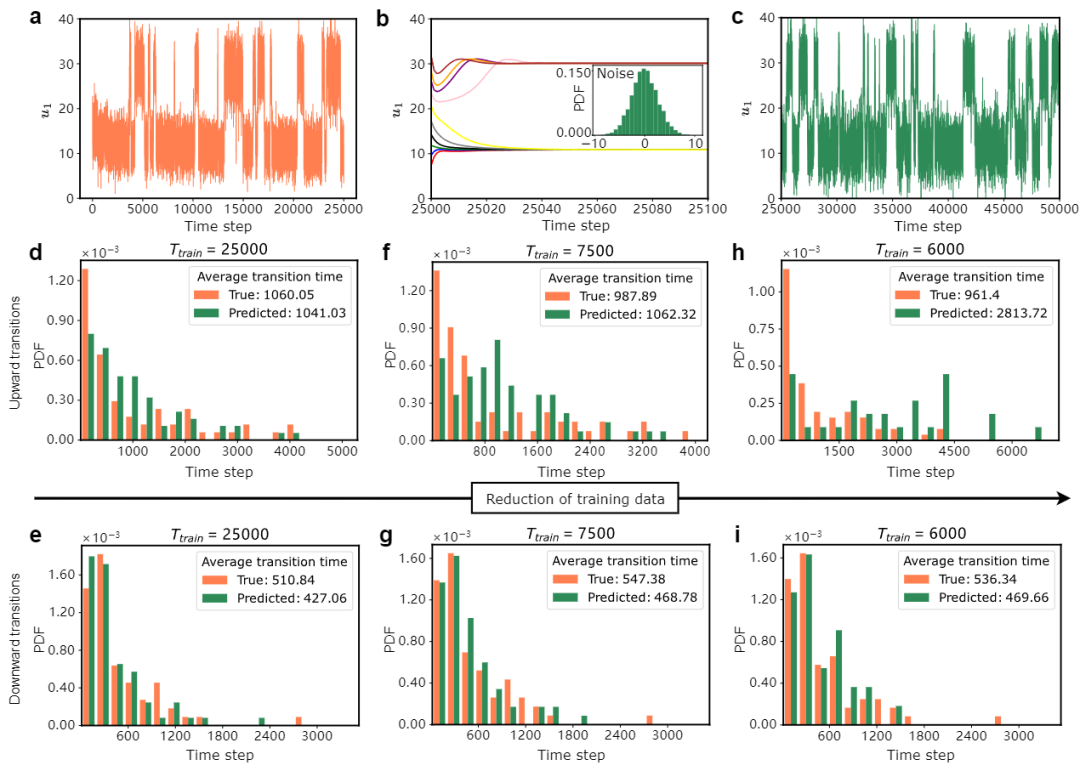
图3:从蛋白质折叠的实验数据中学习噪音诱导的随机转移。u1代表了此蛋白质的端到端长度。不同的长度对应了不同的折叠态。我们将从u1=15转移到u1=30定义为向上的转移,反之则定义为向下的转移。向右指的箭头:减少训练数据的数量。(a) 训练数据的时间序列(0-25000个时间步). (b) 这个训练后慢尺度模型生成了慢尺度的时间序列(彩色线),并且分离得到了噪音的分布。(c) 25000-50000步的预测结果。(d, e)预测数据和测试数据的向上以及向下转移时间的直方图,训练长度(Ttrain)为25000个时间步。转移时间代表连续两次转移之间的时间间隔。(f-i) 相似的关于向上以及向下转移时间的直方图,对于(f, g)训练长度为7500个时间步;对于(h, i)训练长度为6000个时间步。此方法能够准确预测,即使训练长度减少到7500个时间步。
总的来说,作者提供了一个基于随机时间序列数据的通用框架,用于学习噪声诱导的随机转换。作者将这种方法应用于随机微分方程和实验数据的例子中,该方法能够从小规模的训练集中准确学习转换统计量。例如,通过拓展SINDy算法和FORCE学习方法的框架,深化对噪声诱导现象的认识和应用。
https://github.com/Machine-learning-and-complex-systems/NIT-RC
[1] R. Tapia-Rojo, M. Mora, S. Board, J. Walker, R. Boujemaa-Paterski, O. Medalia, and S. Garcia-Manyes, Enhanced statistical sampling reveals microscopic complexity in the talin mechanosensor folding energy landscape, Nat. Phys. 19, 52 (2023).
[2] S. L. Brunton, J. L. Proctor, and J. N. Kutz, Discovering governing equations from data by sparse identification of nonlinear dynamical systems, Proc. Natl. Acad. Sci. 113, 3932 (2016).
[3] K. Kaheman, S. L. Brunton, and J. N. Kutz, Automatic differentiation to simultaneously identify nonlinear dynamics and extract noise probability distributions from data, Mach. Learn.: Sci. Technol. 3, 015031 (2022).
[4] S. Hochreiter and J. Schmidhuber, Long short-term memory, Neural Comput. 9, 1735 (1997). [5] R. R. Labbe, Filterpy documentation (2018).
[6] P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, et al., Scipy 1.0: fundamental algorithms for scientific computing in python, Nat. Methods 17, 261 (2020).
[7] D. Sussillo and L. F. Abbott, Generating coherent patterns of activity from chaotic neural networks, Neuron 63, 544 (2009).
[8] L. B. Liu, A. Losonczy, and Z. Liao, tension: A python package for force learning, PLOS Comput. Biol. 18, e1010722 (2022).
[9] H. Jaeger, The “echo state” approach to analysing and training recurrent neural networks-with an erratum note, Bonn, Germany: German National Research Center for Information Technology GMD Technical Report 148, 13 (2001).
[10] J. Pathak, B. Hunt, M. Girvan, Z. Lu, and E. Ott, Model-free prediction of large spatiotemporally chaotic systems from data: A reservoir computing approach, Phys. Rev. Lett. 120, 024102 (2018).
[11] T. L. Carroll, Using reservoir computers to distinguish chaotic signals, Phys. Rev. E 98, 052209 (2018).
[12] S. H. Lim, L. Theo Giorgini, W. Moon, and J. S. Wettlaufer, Predicting critical transitions in multiscale dynamical systems using reservoir computing, Chaos 30, 123126 (2020).
[13] G. Tanaka, T. Matsumori, H. Yoshida, and K. Aihara, Reservoir computing with diverse timescales for prediction of multiscale dynamics, Phys. Rev. Res. 4, L032014 (2022).
“复杂世界,简单规则”。
集智俱乐部联合复旦大学智能复杂体系实验室青年研究员朱群喜、浙江大学百人计划研究员李樵风、清华大学电子工程系数据科学与智能实验室博士后研究员丁璟韬、美国东北大学物理系Albert-László Barabási指导的博士后高婷婷、北京大学博雅博士后曹文祺、复旦大学数学科学学院应用数学方向博士研究生赵伯林、北京师范大学系统科学学院博士研究生牟牧云,共同发起「复杂系统自动建模」读书会第二季。
读书会将于9月7日每周六晚上20:00-22:00进行,探讨四个核心模块:数据驱动的复杂系统建模、复杂网络结构推断、具有可解释性的复杂系统推断(动力学+网络结构)、应用-超材料设计和城市系统,通过重点讨论75篇经典、前沿的重要文献,从黑盒(数据驱动)到白盒(可解释性),逐步捕捉系统的“本质”规律,帮助大家更好的认识、理解、预测、控制、设计复杂系统,为相关领域的研究和应用提供洞见。欢迎感兴趣的朋友报名参与!

复杂系统自动建模读书会:从数据驱动到可解释性,探索系统内在规律|内附75篇领域必读文献
6. 加入集智,一起复杂!


![]() 输入到训练好的储备池中以生成
输入到训练好的储备池中以生成![]() 。在下一个时间步s+1,输入
。在下一个时间步s+1,输入![]() 是
是![]() 加上从分离出的噪声分布中采样的噪声ηs+1。这个过程称为滚动预测迭代进行,以生成预测时间序列
加上从分离出的噪声分布中采样的噪声ηs+1。这个过程称为滚动预测迭代进行,以生成预测时间序列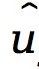 。(c) 对预测转换统计的评估。中间处
。(c) 对预测转换统计的评估。中间处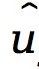 的不同颜色线条代表重复多次的预测。通过转换时间和转换次数的统计量来评估准确性。PDF:概率密度函数。
的不同颜色线条代表重复多次的预测。通过转换时间和转换次数的统计量来评估准确性。PDF:概率密度函数。