许多自然和人为的复杂系统都会出现临界转变,即环境条件的缓慢变化引发系统的突变。这些转变往往会带来严重后果,因此必须提前预测临界转变的发生。7月15日,《物理评论X》(Physical Review X)发表了同济大学物理科学与工程学院、上海自主智能无人系统科学中心严钢教授团队研究提出的“早期定量预测复杂系统中临界点的方法框架”,该方法在各种不同系统上进行验证,并对噪声和不完整数据等具有鲁棒性,且成功预测了真实非洲植被生态系统中森林向稀树草原的临界转变,为预测大型复杂系统临界点应用于真实世界系统提供了重要基础和算法支撑。针对该项成果,美国物理学会《物理杂志》(Physics Magazine)邀请领域知名学者Naoki Masuda教授撰写了题为“Predicting Tipping Points in Complex Systems”的Viewpoint文章。论文第一作者刘子嘉撰文对这项工作进行了深度解读。
研究领域:复杂系统,非线性动力学,网络相变,早期预警,时间序列分析
刘子嘉 | 作者

论文题目:Early Predictor for the Onset of Critical Transitions in Networked Dynamical Systems
论文地址:
https://journals.aps.org/prx/abstract/10.1103/PhysRevX.14.031009
在自然界、技术领域和社会中的复杂系统中,参数的平滑变化可能导致系统状态之间出现显著不同行为的突变[1,2],比如冰期结束时快速全球变暖、沙漠化、动物或细菌物种灭绝事件、停电事件、激光阈值的触发等等。临界转变有可能将系统转移到具有严重不良特性的新状态, 如果没有及时采取纠正措施,就会导致环境破坏、经济损失和公共卫生问题 [3]。因此,如何在早期就对临界转变的具体位置进行定量预测,对预防或避免这些损害至关重要。
针对这一研究领域,学术界始终不断探索前进。传统的早期预警信号(EWS),比如滞后自相关和方差的上升等,多基于临界慢化(CSD)现象,包括一些最新的深度学习方法[4],都可以对临界转变进行预警,但都不能对其发生的具体条件给出定量预测,这无疑降低了方法的实际应用价值。近期提出的一些方法,比如[5]引入贝叶斯线性分段拟合,以及[6]利用储藏池模型来估计转变条件,却都只能应用在低维系统,甚至引入了其他环境信息,大大限制了在真实复杂系统中的应用。
因此,如何仅通过节点状态的时间序列在早期就实现定量预测各种复杂系统中的临界转折点,是一个很重要的挑战。为了应对这个挑战,作者提出了一个全新的深度学习算法,将两种类型的神经网络相结合,构造了GIN-GRU架构。
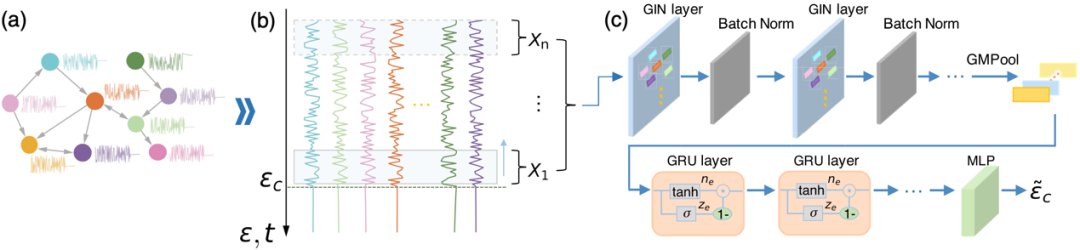
首先需要足够体量的数据,涵盖尽可能多的参数范围,使训练的神经网络足够强大。同时为了实现定量预测临界具体发生条件,数据标签需要足够准确。目前已有很多方法,比如作为耦合振子同步判据的序参量[7],以及更普适的针对连续系统,计算每一个条件下,雅可比矩阵的最大特征值,当临界发生时,其值将会趋近于0。在确定了数据标签后,作者通过一个滑动窗口来构建数据集,如图2(b)所示,每一条数据仅包含所有节点的20个时间步,窗口从临界即将发生一直滑动到系统最开始响应环境变化。
图2. 定量临界预测的方法概述。(a)观测到的时间序列数据以及背后基于的网络拓扑结构。(b)利用滑动窗口构建数据集。(c)GIN-GRU机器学习预测框架。
在构建了海量的训练样本后,数据将被输入到GIN-GRU机器学习架构。首先是GIN(图同构网络)层,读取每个节点的时间序列,识别和提取各个节点的特征,随后经过池化将其整合成整个系统的集体信息。接着GRU(门控循环单元)层读取GIN的输出并解释这些特征,通过自我循环生成记忆,并识别出重要的特征。最后,经过MLP,算法就得到了预测的临界具体条件。得益于在图形模式识别和序列预测方面的卓越性能,在对比和消融实验中,GIN-GRU组合取得了最佳的预测效果。
论文中分别举了一阶相变和二阶相变的三个例子来论证方法的有效性,这里以较难的神经科学领域的一阶相变进行具体介绍。Wilson-Cowan系统描述了神经元群体的放电率活动,如图3(a)所示,当横坐标神经元间连边强度降低比例逐渐增加,神经元的平均活性发生了一次显著的突变,与此同时,如绿线所示最大特征值也趋近于0,即发生了临界转变。
图3. Wilson-Cowan神经系统的定量临界预测。(a)系统变化规律及表征临界的指标展示。(b)不同Lead Distance的预测结果展示。(c)全部测试数据集的预测平均相对误差随Lead Distance的变化规律。
图3(a)和图3(b)是从Wilson-Cowan系统测试集中随机选择的一个样例,图3(b)展示了从不同环境控制变量开始预测的结果,不同的红点表示着定量预测的临界条件,从颜色条可以看出对应的预测相对误差很小。图3(c)统计了随着开始预测时环境控制变量与临界条件之间的距离(Lead Distance)减小,平均相对误差的变化规律,可以看出不仅在临界转变附近表现出高预测准确性,而且随着Lead Distance逐渐增加,预测平均相对误差趋于平稳,并保持在合理水平以下。
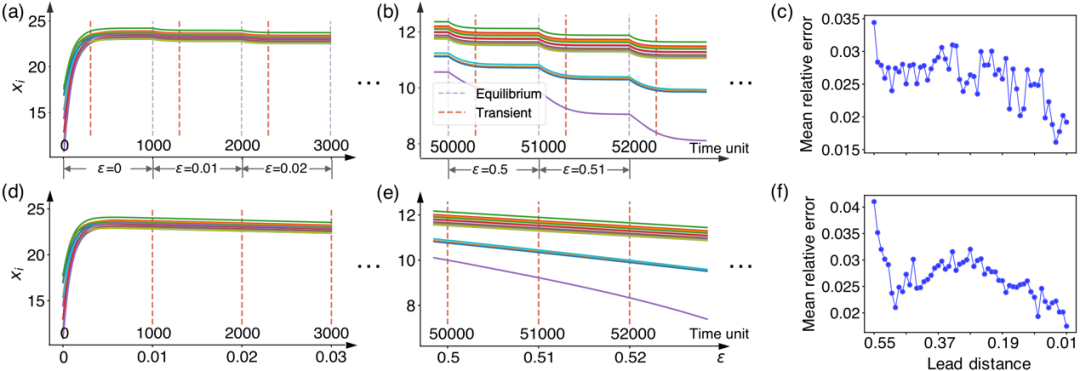
在实践中,观测噪声是普遍存在的,很难观察到所有变量的时间序列,并且系统不一定在所有环境变量下都响应到平衡状态。因此,文中验证了GIN-GRU方法对于不完整数据、观测噪声和瞬态数据的鲁棒性。
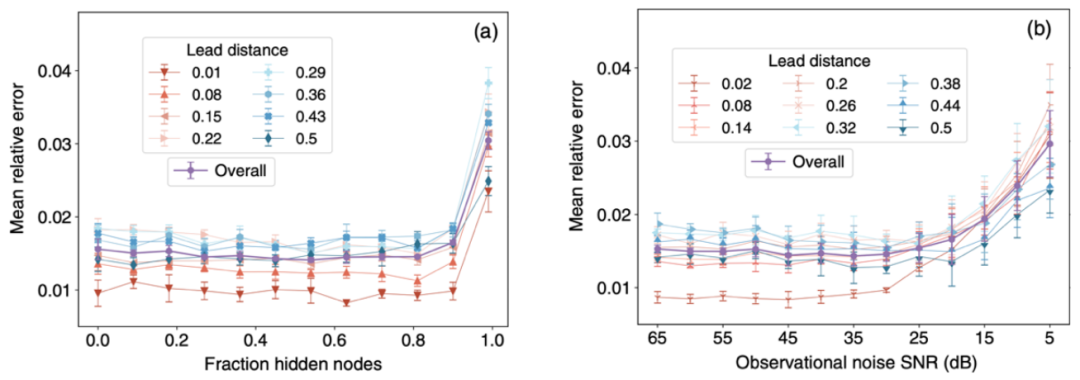
图4. GIN-GRU方法对于数据不完整以及观测噪声的鲁棒性验证。
从图4看出即使81%的节点被隐藏或者观测噪声的信噪比达到35dB,GIN-GRU方法依然保持着与完整不加噪声的数据相当的预测准确度。
图5. GIN-GRU方法对于瞬态数据的鲁棒性验证。(a)、(b)缩短系统演化时间。(d)、(e)系统对环境变化的实时响应。(c)、(f)预测平均相对误差随Lead Distance的变化规律。
图5揭示了对于瞬态数据,甚至对环境变化实时响应,GIN-GRU方法依然保持了相当的鲁棒性。
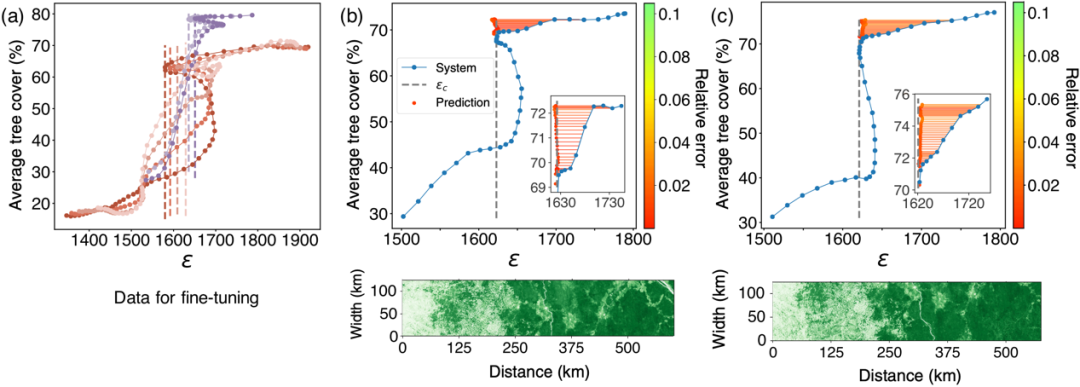
真实系统往往具有数据量极少和数据间差异性大的特点,文章接着以非洲植被生态系统为例展示了方法对于真实系统的临界预测的迁移与应用。在半干旱地区,生态系统可能经历从森林到稀树草原的突然转变。图6(a)展示了两个地区(红色和紫色线)的6条平均树木覆盖率随着横坐标环境控制变量年平均降雨量的变化曲线,已经是全部用来训练和学习的数据,可以看出两个地区本身的变化规律也有很大差异。针对这些真实系统新的挑战,作者采用了类似大模型的训练思路。先通过多个理论模型的庞大体量,训练出一个经验丰富的预训练模型,然后利用这6条真实数据进行模型微调,去捕捉和适应新的真实系统的底层规律。最后作者在一个全新的第三个地区的2条数据上进行测试,结果如图6(b)和图6(c)所示,可以看出即使在降雨量很充沛时开始预测临界点,预测的准确度依然很高。
图6.真实非洲植被生态系统的临界预测。(a)用来微调的两个地区真实数据。(b)、(c)第三个地区的临界预测结果以及实际树木覆盖率展示。
定量临界预测的探索还有诸多方向。首先,滑动窗口的大小目前设置为20,虽然这已经相对较小,但值得研究的是在仍能提供准确预测的情况下可以使用多小的窗口大小。其次,一些复杂系统可能会经历多次临界转变[8],仅基于临界转变前的数据来预测所有转变的发生是一个具有挑战性但很有价值的目标。第三,在复杂系统中,节点可以具有高阶相互作用,并且这种相互作用可能会影响网络系统的转变[9]。因此,将方法扩展到预测更高阶网络的临界点是一个有趣的方向。最后,关于在理论数据进行预训练以预测实际系统临界转变的框架,将更多理论系统整合以增加预训练模型的适用性是值得未来考虑和努力实现的事情。
[1] M. Scheffer, S. Carpenter, J. A. Foley, C. Folke, and B. Walker, Catastrophic shifts in ecosystems, Nature (London) 413, 591 (2001).
[2] M. Scheffer, Critical Transitions in Nature and Society (Princeton University Press, Princeton, NJ, 2020), Vol. 16.
[3] D. Eroglu, M. Tanzi, S. van Strien, and T. Pereira, Revealing dynamics, communities, and criticality from data, Phys. Rev. X 10, 021047 (2020).
[4] T. M. Bury, R. Sujith, I. Pavithran, M. Scheffer, T. M. Lenton, M. Anand, and C.T. Bauch, Deep learning for early warning signals of tipping points, Proc. Natl. Acad. Sci. U.S.A. 118, e2106140118 (2021).
[5] M. Heßler and O. Kamps, Bayesian on-line anticipation of critical transitions, New J. Phys. 24, 063021 (2022).
[6] H. Fan, L.-W. Kong, Y.-C. Lai, and X. Wang, Anticipating synchronization with machine learning, Phys. Rev. Res. 3, 023237 (2021).
[7] M. Schröder, M. Timme, and D. Witthaut, A universal order parameter for synchrony in networks of limit cycle oscillators, Chaos 27, 073119 (2017).
[8] J. J. Lever, I. A. van de Leemput, E. Weinans, R. Quax, V. Dakos, E.H. van Nes, J. Bascompte, and M. Scheffer, Foreseeing the future of mutualistic communities beyond collapse, Ecol. Lett. 23, 2 (2020).
[9] F. Battiston, E. Amico, A. Barrat, G. Bianconi, G. Ferraz de Arruda, B. Franceschiello, I. Iacopini, S. Ke ́fi, V. Latora, Y. Moreno et al., The physics of higher-order interactions in complex systems, Nat. Phys. 17, 1093 (2021).
“复杂世界,简单规则”。
集智俱乐部联合复旦大学智能复杂体系实验室青年研究员朱群喜、浙江大学百人计划研究员李樵风、清华大学电子工程系数据科学与智能实验室博士后研究员丁璟韬、美国东北大学物理系Albert-László Barabási指导的博士后高婷婷、北京大学博雅博士后曹文祺、复旦大学数学科学学院应用数学方向博士研究生赵伯林、北京师范大学系统科学学院博士研究生牟牧云,共同发起「复杂系统自动建模」读书会第二季。
读书会将于9月7日每周六晚上20:00-22:00进行,探讨四个核心模块:数据驱动的复杂系统建模、复杂网络结构推断、具有可解释性的复杂系统推断(动力学+网络结构)、应用-超材料设计和城市系统,通过重点讨论75篇经典、前沿的重要文献,从黑盒(数据驱动)到白盒(可解释性),逐步捕捉系统的“本质”规律,帮助大家更好的认识、理解、预测、控制、设计复杂系统,为相关领域的研究和应用提供洞见。欢迎感兴趣的朋友报名参与!
![]()
复杂系统自动建模读书会:从数据驱动到可解释性,探索系统内在规律|内附75篇领域必读文献
6. 加入集智,一起复杂!