最近,北京师范大学珠海校区-复杂系统国际科学中心副教授刘宇等人在 Nature 旗下子刊 npj Complexity 杂志发表最新研究,用梯径(Ladderpath)方法研究神经网络的结构复杂度,并指出其结构复杂度与功能表现之间的关系。这为我们提供了一个看待神经网络的新视角。
刘宇老师是集智俱乐部「AI By Complexity」读书会的发起人之一。「AI By Complexity」读书会探究如何度量复杂系统的“好坏”?如何理解复杂系统的机制?这些理解是否可以启发我们设计更好的AI模型?在本质上帮助我们设计更好的AI系统。读书会于6月10日开始,每周一晚上20:00-22:00举办。欢迎从事相关领域研究、对AI+Complexity感兴趣的朋友们报名读书会交流!
研究领域:神经网络,算法复杂性,算法信息论,梯径理论
张章、刘宇 | 作者
ecsLab | 来源

论文题目:Correlating measures of hierarchical structures in artificial neural networks with their performance
论文地址:https://www.nature.com/articles/s44260-024-00015-x
我们最近在Nature旗下的《npj Complexity》杂志发表了一篇题为《Correlating measures of hierarchical structures in artificial neural networks with their performance》的研究论文,讲述如何用梯径(Ladderpath)方法来研究神经网络的结构复杂度,并指出其结构复杂度与功能表现之间的关系。
这是梯径(Ladderpath)方法的第4篇已发表的研究论文(还有一篇正在返修中):
-
第1篇发表在《Science Advances》—— Exploring and mapping chemical space with molecular assembly trees(主要是前序视角和观点)
-
第2篇发表在《Entropy》—— Ladderpath approach: How tinkering and reuse increase complexity and information (提出梯径的概念、基本方法和算法)
-
第3篇发表在《Physical Review Research》—— Evolutionary tinkering enriches the hierarchical and nested structures in amino acid sequences(将梯径用在蛋白序列上)
-
第4篇即这篇,发表在《npj Complexity》(将梯径概念扩充并用在蛋白序列上)
-
第5篇关于多肽药物的设计,目前正在第二轮返修中
非常感谢北京师范大学的张章同学(北师大张江老师的博士生,集智俱乐部资深成员)为这篇文章做了一个讲解视频(微信视频号“张章2050”)。我觉得讲得非常好,这里就直接借用他的一部分稿子对本文进行介绍。
这篇文章讲了这样一个故事,说机器学习中神经网络的训练,在某种程度上与生命的演化过程是高度相似的。不严格地讲,生命在演化过程中,是由简单的元素逐渐组合,形成越来越复杂的个体和结构。由随机碰撞的有机分子直接组成生物体的概率实在是太低,那么简单的有机分子可能组成相对简单的氨基酸,这个就容易一点,氨基酸在作为基本单位去碰撞,组合形成蛋白质,蛋白质再作为基本单位去形成更高级,更复杂的组织。所以我们去看一个复杂的生物体,实际上是一级一级组合出来的,每一级的组件都在高度复用。而我们去看神经网络的结构,发现也是这样,虽然我们开始训练神经网络的时候没这么想,但是我们去看训练完成的神经网络,会发现它里面存在着一层一层,层级化的,高度复用的基本组件。换句话说,好的神经网络不仅loss低,它的结构本身也存在高度的复杂性。
在研究生命演化的过程中,我们之前提出了梯径
(Ladderpath)方法,来度量一个系统的复杂度,本篇文章是梯径方法在神经网络上的应用。我们接下来会首先介绍梯径方法的基本思路,然后介绍如何把这个方法应用到神经网络上,最后看看有哪些结论。
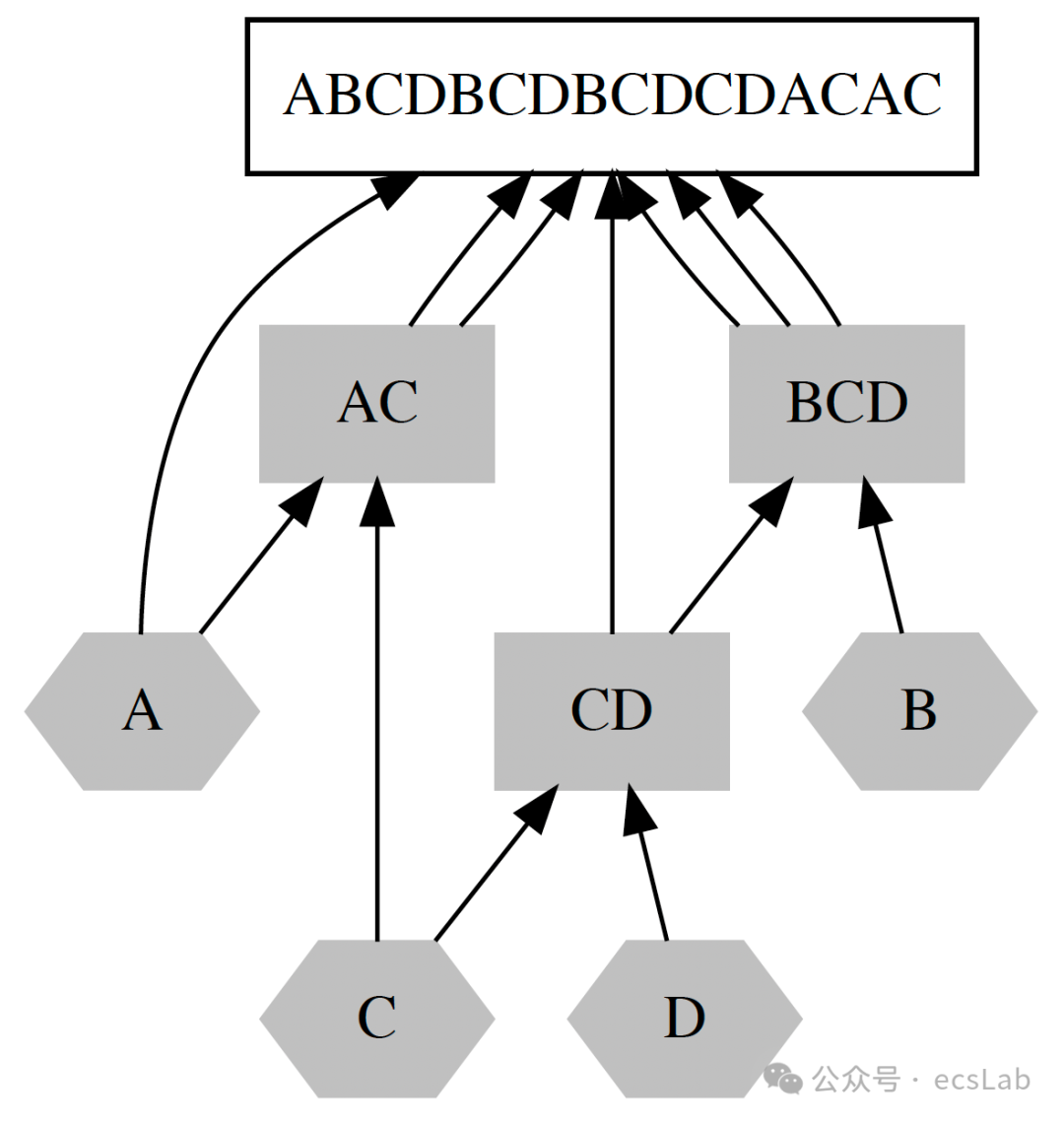
梯径方法是用来衡量一个系统复杂度的方法,这种复杂度可以被理解为有序程度和随机程度的综合。让我们用一个最简单的例子来理解梯径方法如何工作,假设有一个序列,“ABCDBCDBCDCDACAC”,我们可以怎样组合出这个序列呢?
首先我们有ABCD这四个基本元素,然后我们第1步用已有元素C和D组成CD,第2步用A和C组成AC。这时候我们就有了六个基本元素,第3步我们用B和CD组成BCD,这时候我们有了7个基本元素,然后我们就可以去组合最终字符串了,第四步我们用A和BCD组合成ABCD,这是最终字符串的前四个字符,第五步我们再用前四个字符组合一个BCD,就得到了前7个字符,这样我们每一步,把两个元素组合,最后用九步组合出完整字符串,第十步,我们输出目标字符串。这个字符串有16个字符,我们用10步把它组合并输出出来。这是因为有些元素被重复利用了,例如BCD就被重复利用了三次。这里的10,我们把它叫做梯径度,用16-10等于6,这个6我们叫它有序度。
让我们设想,假设这个序列16个字母全都是A,那么组合出来就会很容易,两个A组合成AA,然后两个AA组合成AAAA,四步就能搞出来这个序列,第五步输出,那么梯径度就是5,所以有序度就是16-5=11,非常有序。如果这个序列非常混乱,比如“ABCDEFGHIJKLMNOP”,也没有什么可以重复用的,那么组合这个序列就很麻烦,第一步你组合A和B,第二步你组合AB和C,以此类推,你就得用15步才能把这个序列组合出来,第十六步输出,所以梯径度就是16,有序度那自然就是0。
给定一个序列长度,再规定好基本元素数量,有序度就会有一个范围。这个例子中是0到11,我们利用这个长度下梯径度的最大值和最小值,将这个序列的梯径度值进行归一化,即得到该序列的有序率η;也就是说完全随机的序列其η为0,完全有序的序列其η为1。这个量就是与系统尺度无关的系统复杂度的度量,因为任何一个尺寸的系统,都可以用这样一个0-1之间的数来衡量。
然后让我们来考虑这个问题,一个系统有多大的η才算比较“好”呢?从直观出发,如果η特别大,系统就始终只由一类重复元素构成,那么这个系统很可能没什么复杂的功能,如果η特别小呢,这个系统的构成就没什么规律,每个元素只出现一次,没有元素重复,这样这个系统就没什么复用的模块,很松散。“好”的系统,可能是有一定程度的复用,但是每次复用又会有一些变化和多样性,所以η可能不大不小,可能会在0.5左右。
接下来我们把这些理论基础应用到神经网络结构的度量上。你可能会好奇,就是前面说的梯径方法,是度量序列的,但是神经网络,比如多层感知机,他是一个网络结构,不是序列。所以我们需要把神经网络序列化,而序列化的基本思路,因为神经网络中有不同的信息传输路径,每个路径就是一个序列,所以我们可以自然的用一些序列来表示神经网络结构。
现在我们来考虑神经网络如何拆成信息传输路径组成的序列,第一步是离散化,把连续的网络权重变成离散的几个。然后把所有由前到后的路径遍历出来,例如在这张图上,离散化后有三个权重,xyz,那么信息经过第一层的第一个神经元到第二层的第一个神经元,再到第三层的第一个神经元就用路径,AxBzC来表示。这里要注意的一点是,神经网络的一切要素都在权重,所以我们给权重离散化并且编号xyz ,而神经元只代表层数,第一层的第一个神经元和第二个神经元没有什么本质的不同,他们的不同是所连接的权重的不同带来的,而他们上面的运算都是一样的,都是加权求和,激活函数。所以神经元不需要编号,他只代表层数。这样我们就把这个神经网络遍历一遍,得到很多字符串,有了这些字符串,我们就可以计算神经网络的复杂度η了。
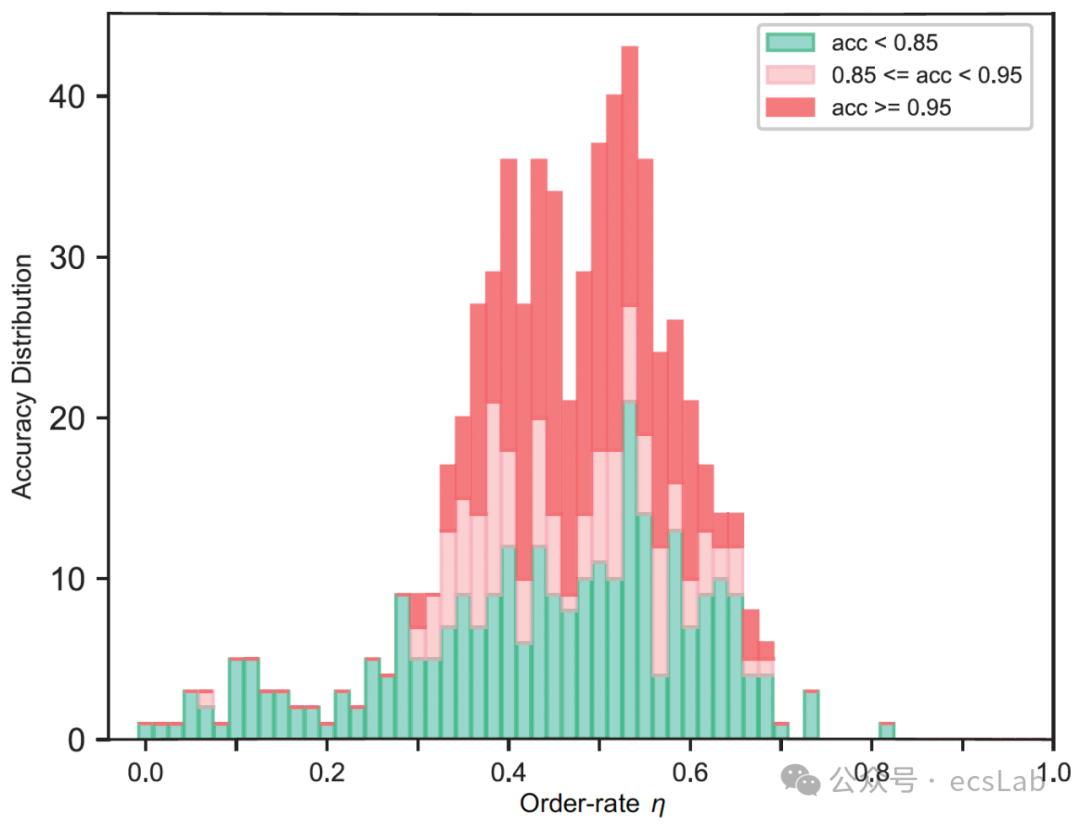
实验结果证明了我们的期待,复杂度η和神经网络的表现密切相关,下面这个图可以证明,在很多神经网络上,η越接近0.5左右的那些网络,就是红色的那些柱子,解决任务的准确率越高。
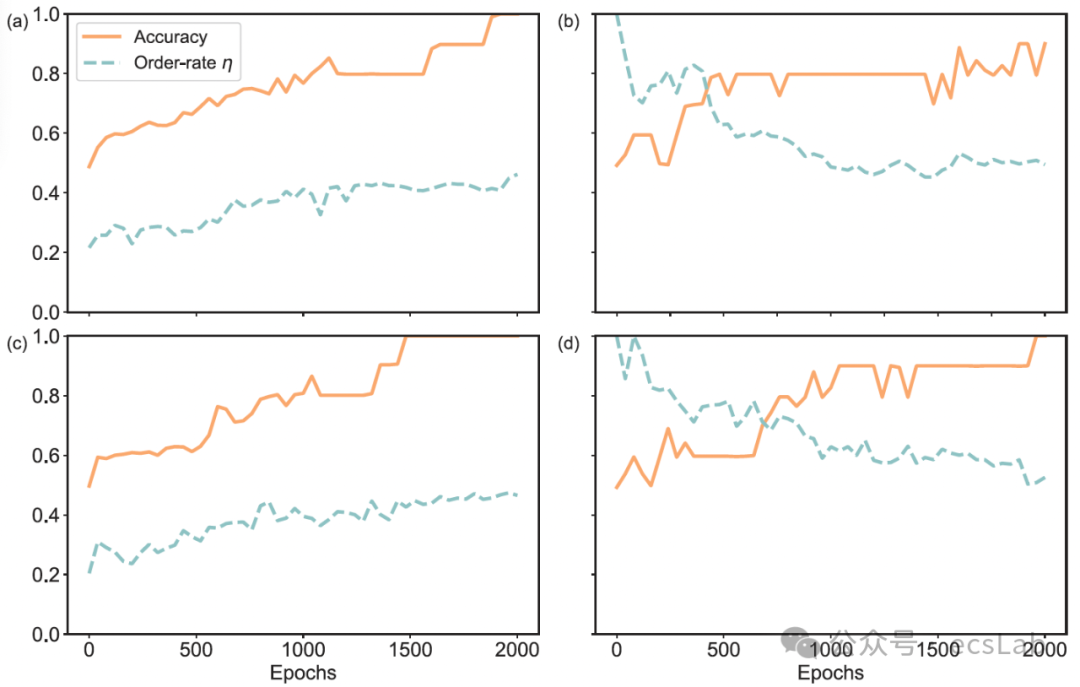
接下来这张图,横坐标是训练轮数,这张图有两条线,橙色线表示神经网络准确率随训练过程的变化,蓝色线标表示η随训练过程的变化。我们可以看到,一开始我们随机初始化神经网络,它的η可以在任何地方,但是随着训练的进行准确率越来越高,这个η也会越来越趋向于0.5。这说明神经网络训练的过程不是一个完全的黑箱。从内部结构来看,是一个内部组件丰富度越来越高,组件复用度也越来越高,从而逐渐趋向最高复杂度的过程。
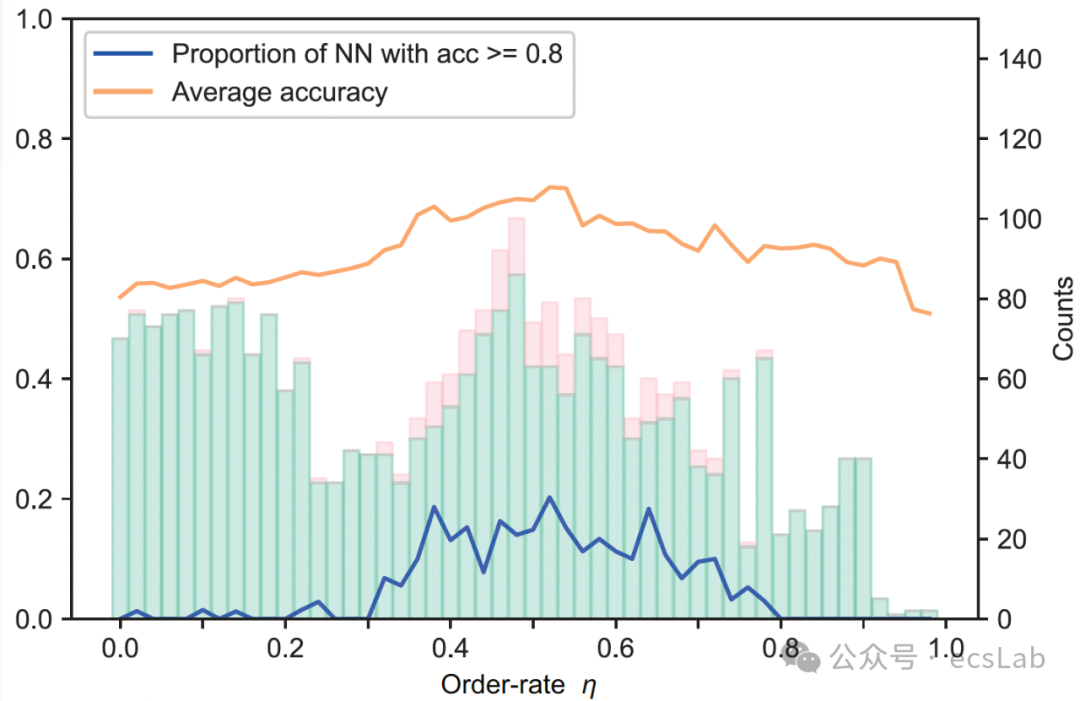
那么这个方法有什么用呢,有一个直观的作用就是神经网络的权重初始化。我们可以说,既然η在0.5左右比较好,那么能不能直接把权重的初始分布设置为0.5左右,这样训练起来会不会更容易呢,这个结果也说明的确是这样的(下图)。这里的横坐标是初始化时的神经网络的η,纵坐标是模型的准确率,黄线是平均准确率,蓝线是准确率大于80%的神经网络占比,可以看到这些线都在横坐标是0.5左右达到最高,说明好的初始化的确可以让神经网络的训练更高效。
这篇文章另外的一个点在于它给我们提供了一个看待神经网络的另一个视角,除了紧紧盯着loss之外,我们还可以从结构本身看出神经网络的好坏,而这种结构的度量背后又有深刻的复杂性理论,和算法信息论息息相关。
目前这个工作是通过将一个神经网络序列化来表征它的结构的;但事实上,这只是一个权宜之计,原则上,梯径方法也是直接适用于Graph的,可以直接去寻找Graph中重复使用的subgraphs,这是后续的研究方向。
最后说明一点,虽然这个工作中做的神经网络的参数并不是很多,这是因为(当时的)梯径算法能处理的序列长度有限。事实上,最近梯径算法有了突破,能处理长度在千万级的序列了,所以算法的应用场景扩大了很多。
感谢合作者厦门大学数学学院周达教授以及许卓莹、朱应俊两位同学的付出,和北师大珠海校区物理学院洪斌斌副研究员,以及吴鑫霖、张竞文、蔡沐峰三位本科同学的帮助。
刘宇,副教授,北京师范大学珠海校区-复杂系统国际科学中心-Evolving Complex Systems Lab。物理、数学背景(瑞典Uppsala大学应用数学与统计博士),先后在英国Glasgow大学化学系、荷兰Groningen大学化学生物系、瑞典Mittag-Leffler数学研究所任研究职位。目前研究方向:用算法信息论研究生命的起源与演化,即,把生命系统定量刻画成软件系统。微信公众号:【ecsLab】。
大模型、多模态、多智能体层出不穷,各种各样的神经网络变体在AI大舞台各显身手。复杂系统领域对于涌现、层级、鲁棒性、非线性、演化等问题的探索也在持续推进。而优秀的AI系统、创新性的神经网络,往往在一定程度上具备优秀复杂系统的特征。因此,发展中的复杂系统理论方法如何指导未来AI的设计,正在成为备受关注的问题。
集智俱乐部联合加利福尼亚大学圣迭戈分校助理教授尤亦庄、北京师范大学副教授刘宇、北京师范大学系统科学学院在读博士张章、牟牧云和在读硕士杨明哲、清华大学在读博士田洋共同发起「AI By Complexity」读书会,探究如何度量复杂系统的“好坏”?如何理解复杂系统的机制?这些理解是否可以启发我们设计更好的AI模型?在本质上帮助我们设计更好的AI系统。读书会于6月10日开始,每周一晚上20:00-22:00举办。欢迎从事相关领域研究、对AI+Complexity感兴趣的朋友们报名读书会交流!
![]()
6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会