关键词:复杂网络,人类网络,Kuramoto模型,同步,全局最优
![]()
论文名称:How synchronized human networks escape local minima
论文地址:https://www.nature.com/articles/s41467-024-53540-7
期刊名称:Nature Communications
寻找全局最小值同时避免局部最小值是许多复杂网络的挑战。这对于人类网络来说也是至关重要的,我们需要适应冲突、气候和灾害等不断变化的外界条件,并寻找新的稳定状态,而这一过程的实现机制尚不清楚。近期发表在Nature Communications 上的一篇研究,揭示了人类网络是通过改变耦合强度或节奏的方式,以抵抗外界干扰实现稳健状态。
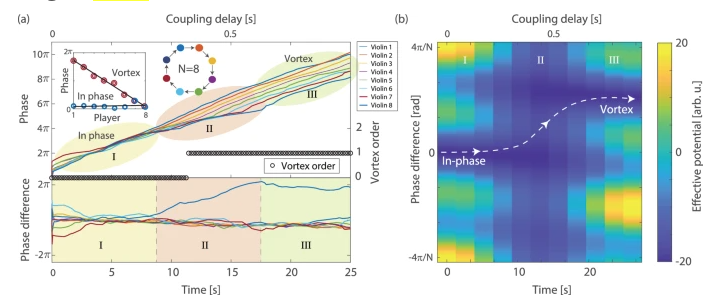
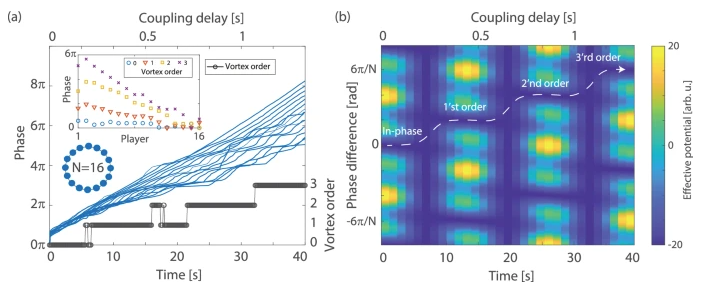
研究者使用小提琴演奏者形成的单向闭环拓扑结构和时延耦合的人类网络开展研究,网络具有明确定义的局部和全局最小值。每次实验开始时,所有演奏者之间的时延为零 Δt = 0,耦合强度足够高,所有演奏者处于同相状态,同时还演奏同一音符。然后,研究者将Δt随时间线性增加为Δt = t/30。当Δt超过 nT/N(其中N为整数)时,同相状态变为局部最小值,全局最小解为旋涡状态,其中每个演奏者和相邻者之间有相同的延迟。演奏者必须离开他们的同相状态并找到旋涡状态。参数 n 表示稳定涡的阶数。当涡阶为零时,n = 0,系统处于同步同相状态,n = 1 处于第一个漩涡阶,演奏者之间的延迟相加等于2π。对于更高的漩涡顺序,增加演奏者的延迟等于2π的更高倍数。
通过Kuramoto模型分析耦合演奏周期性节奏的动力学发现,演奏者可以通过自动调整网络的局部属性,如速度、振幅和演奏者之间的耦合强度,来避开局部最小值。进一步地,研究者提出并分析了人类网络中的四种动态过程,以解释该现象:
第一个动态过程中,一些演奏者忽略了接收到的信号,从而降低了与相邻者的有效耦合强度。然后,他们可以自由地扩散它们的相位以达到旋涡状态。第二个动态过程中,演奏者放慢了他们的节奏,所以同步状态对于任意大的延迟都保持全局最小值。第三个动态过程中,演奏者们进一步放慢节奏,直到每个人都无限期地演奏同一个音符。这种状态被称为振荡死亡,是一种稳定的同步方案,与时间延迟无关。然后演奏者会自发地从振荡死亡状态直接进入全局稳定的漩涡状态。第四个动态过程中,一些演奏者停止演奏(即将其振幅降低到接近零)。在这种被称为振幅死亡的状态下,网络拓扑变为开环,其中局部极小值及其势垒消失。因此,让其他演奏者都能够找到旋涡状态。
图1. 单向耦合闭环网络上的小提琴演奏者,其中每个演奏者只能听到其右侧的演奏者。(a) N=6的耦合示意图。(b) 周期性重复的乐句说明了两种可能的同步状态:同相状态,即所有演奏者同时演奏同一个音符;旋涡状态,即由于时间延迟,每个演奏者都在演奏不同的音符。(c) 对于两个延迟值Δt,系统的有效电位是演奏者之间相位差的函数。当Δt = 0时,电势最小相位差为零,处于同步同相状态。当Δt = T/N时,最小电位在2π/N处,表明处于旋涡状态,同相态在势垒的保护下成为局部最小值。(d) 有效电位图是演奏者之间相位差和延迟耦合的函数。
图 2. N = 8个演奏者位于一个单向耦合的环上,从同步的同相状态出发,找到涡旋状态的过程。
图 3. N = 16个演奏者位于一个单向耦合的环上,相位扩散,并达到高阶漩涡状态。
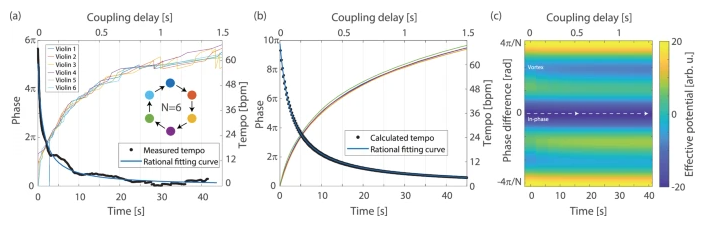
图4. N = 6个演奏者位于一个单向耦合的环上,节奏减慢。
彭晨 | 编译
6. 加入集智,一起复杂!