重整化群方法如何应用在网络科学中?Nat. Rev. Phys. 综述
摘要
重整化群(RG)是一种强大的理论框架。它被用于具有多自由度的系统,以在不同分辨率水平上转换其配置描述,以及相关的模型参数和耦合常数。重整化群还提供了一种识别相变临界点并研究其周围系统行为的方法。在传统的物理应用中,重整化群主要基于同质性、对称性、几何和局部性的概念来定义度量距离、尺度变换和自相似的粗粒化方案。最近,人们努力将重整化群的概念扩展到复杂网络。然而,在这类系统中,明确的几何坐标不一定存在,不同的节点和子图可能具有不同的统计特性,而且不存在均匀的晶格对称性——所有这些特征都使得定义一致的重整化程序变得复杂。在这篇技术综述中,我们讨论了网络重整化的主要方法、重要进展以及仍然存在的开放性挑战。

论文题目:Network renormalization
发表时间:2025年3月26日
论文地址:https://doi.org/10.1038/s42254-025-00817-5
期刊名称:Nature Reviews Physics
集智社区对重整化群方法的导读,以及重整化群与机器学习的碰撞:重整化遇见机器学习:多尺度视角探索复杂系统内在的统一性
重整化群(Renormalization Group,RG)是物理学中研究多体系统相变和普适性现象的核心工具。它通过逐层“粗粒化”微观自由度,揭示系统在不同尺度下的有效行为。然而,传统RG依赖均匀性、对称性和几何局域性等假设,难以直接应用于复杂网络——这类系统通常缺乏显式几何嵌入、节点异质性强,且具有小世界性(Small-World Property)和模块化结构。近年来,研究者试图将RG思想拓展至复杂网络,以解析其跨尺度的统计规律和动力学行为。Nature Reviews Physics最新技术综述系统梳理了这一领域的方法进展、关键挑战与未来方向。
复杂网络重整化的核心挑战
复杂网络重整化的核心挑战
复杂网络(如社交网络、生物网络、经济网络)的拓扑异质性和结构不规则性,使得传统RG的三大步骤:定义粗粒变量、平均微观涨落、重整化耦合参数,面临根本上的困难。例如,在均匀晶格中,通过划分相同尺寸的“块节点”即可实现粗粒化,但复杂网络的节点度分布宽泛、路径长度短且聚类系数高,无法直接定义一致的粗粒化单元。此外,网络动力学(如流行病传播、金融冲击传导)与拓扑结构的耦合,要求粗粒化过程必须保持动力学的一致性,而非仅关注静态结构。
作者指出,复杂网络的重整化需解决传统RG提出的三大问题:
1. 如何定义粗粒变量:在无几何坐标的网络中,需依赖拓扑特征(如最短路径、模块化社区)或动力学等效性(如扩散过程)划分块节点。
2. 如何保留跨尺度相关性:小世界性使得长程连接普遍存在,局域涨落的平均化可能破坏关键的长程关联。
3. 如何重整化参数:若网络本身是随机图模型(Random Graph),需将微观参数分布映射到粗粒尺度,并追踪其流方程(Flow Equation)。
网络粗粒化的五大路径
网络粗粒化的五大路径
1. 基于最短路径的几何方法
早期尝试借鉴分形几何的“盒子覆盖法”(Box-Covering Method),将网络节点按最短路径距离分组,生成自相似的重整化序列。尽管该方法能揭示某些网络(如分形网络)的标度行为,但小世界性导致路径距离无法有效区分不同尺度,聚类系数(Clustering Coefficient)等关键性质在粗粒化后可能丢失。
2. 谱方法(Spectral Methods)
以网络拉普拉斯矩阵(Laplacian Matrix)的谱分解为基础,保留主导特征值和特征向量以粗粒化网络。例如,随机游走(Random Walk)的扩散过程可通过截断高频模态(Fast Modes)实现动力学等效的粗粒化。谱方法在同步(Synchronization)和可控性(Controllability)研究中表现突出,但其计算复杂度高,且依赖特定动力学假设。
3. 拓扑方法(Topological Methods)
基于节点中心性(如度值)、结构等价性(Structurally Equivalent Nodes)或社区结构划分块节点。典型方法包括度阈值化(移除低度节点)和k核分解(保留高度互连的子图)。此类方法能揭示网络的层次自相似性,但依赖于预设的拓扑模式,无法普适应用于无显著社区结构的网络。
4. 对称性方法(Symmetry-Based Methods)
利用网络的动力学对称性(如输入树等价性)定义粗粒分区。例如,纤维着色(Fibration Coloring)通过节点输入树的同构性合并等效节点,保留动力学同步性。然而,对称性方法通常仅能识别单一分区,且无法迭代应用于非对称网络。
5. 工程与机器学习驱动的方法
为降低计算成本,图神经网络(Graph Neural Networks)采用启发式粗粒化策略(如边权重聚合、节点嵌入求和)。尽管实用性强,这类方法缺乏对网络多尺度本质的理论解释,属于“任务导向”而非“原理导向”。
三大前沿重整化框架
三大前沿重整化框架
几何重整化(Geometric Renormalization)
复杂网络中的空间局域性可以在几何框架下得到恢复。通过将现实世界中结构异质性和非局域性的网络嵌入到双曲空间中,恢复结构的几何局域性,进而实现尺度变换。每个节点被赋予“流行度”(Popularity,对应径向坐标)和“相似度”(Similarity,对应角坐标)唯独,连接概率由双曲距离决定。粗粒化时,将相邻节点合并为超节点,并重新计算坐标与耦合参数。该方法成功预测了人脑连接组(Connectome)的多尺度自相似性,并可通过逆向的“几何分支生长”(Geometric Branching Growth)生成统计等效的细粒度网络。
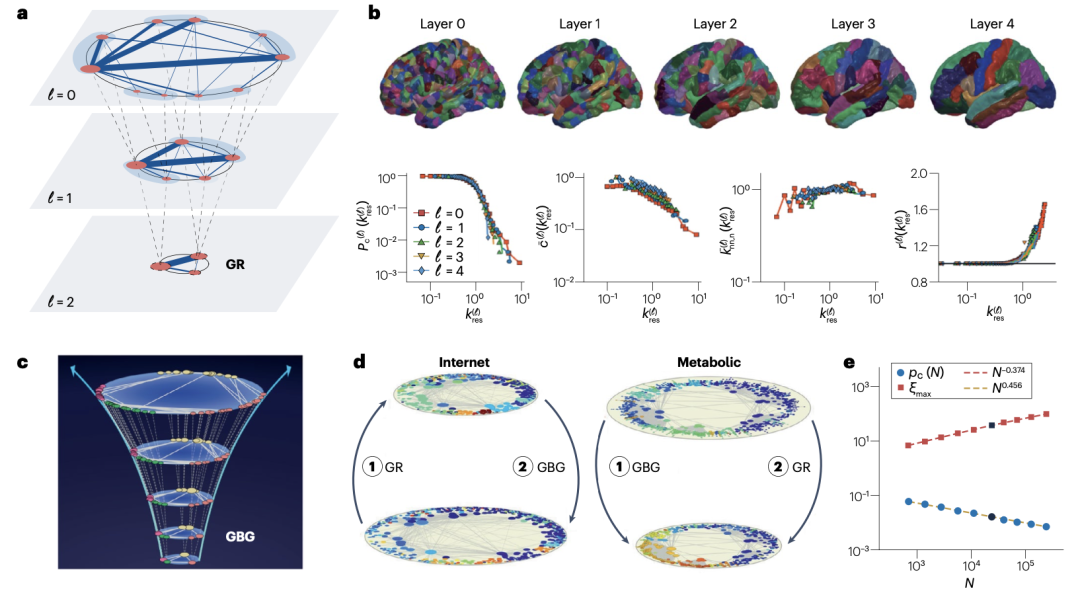
图 1. 真实网络上几何网络重整化的直接方法(Directed)和逆方法(inverse)与结果。
拉普拉斯重整化(Laplacian Renormalization)
另一种用于复杂网络重整化的通用方法,采用节点间的Laplacian扩散概念检测多尺度结构,从而对一般网络的顶点和边进行粗粒化,最终实现对网络动力学进行重整化。这一方法类似于前一节中描述的几何方法,也可以在直观且具有物理意义的实空间中加以表述,与统计物理中的Migdal–Kadanoff重整化群方法高度相似。这种重整化方法的独特之处在于,它以对偶或k空间表示的形式进行了严格表述,在这两种情形下,该方法都引入了一种迭代的网络粗粒化方案,能够在不断扩大的时空尺度上保留其扩散动力学特征。该方法的实空间版本类似Kadanoff的块自旋重整化,而k空间版本则类比Wilson的连续场论RG,能解析网络的谱维度(Spectral Dimension)和拓扑相变。例如,随机块模型(Stochastic Block Model)的社区结构可通过扩散容量(Diffusive Capacity)的峰值检测。
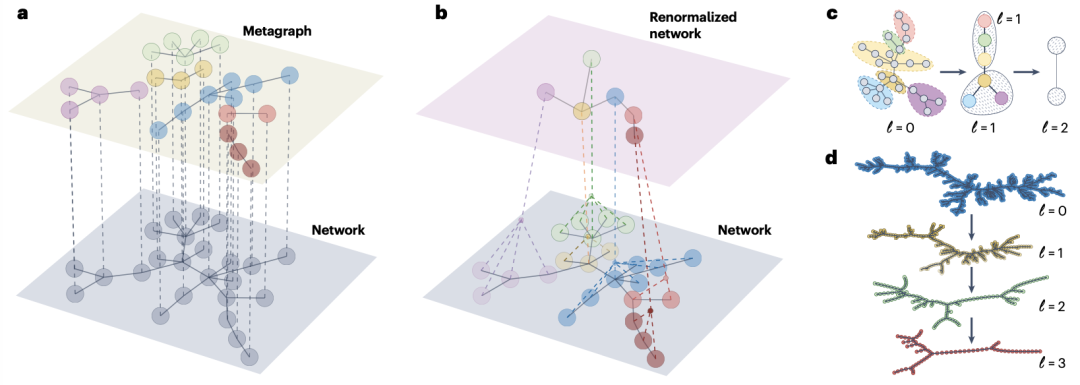
图 2. 拉普拉斯重整化中的实空间构造。
多尺度重整化(Multiscale Renormalization)
提出了一种“聚合不变”的随机图模型,其随机变量在节点划分后仍然在统计分布上保持一致。模型假设连接概率由节点的适应度(Fitness)和对偶效应(Dyadic Effects)共同决定,粗粒化后参数按加和或最大似然规则重整化。该方法成功复现了国际贸易网络的多尺度特性,且能通过逆向细粒化(Fine-Graining)生成无限可分(Infinitely Divisible)的微观网络。其“淬火”版本(Quenched Variant)利用实际经济数据(如GDP)作为适应度,而“退火”版本(Annealed Variant)则通过稳定分布(Stable Distribution)生成无标度(Scale-Free)网络。
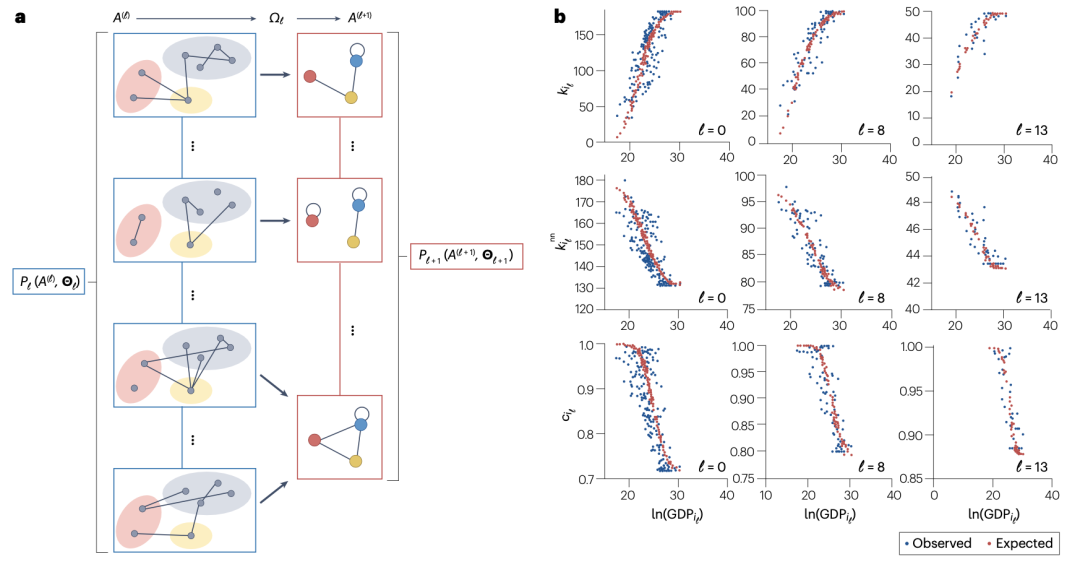
图 3. 多尺度网络重整化方法。
未来挑战与跨学科启示
未来挑战与跨学科启示
1. 分辨率的本质性:需区分网络内在尺度与数据观测限制。例如,金融网络的微观链接因隐私问题不可见,而流行病接触网络仅部分已知。
2. 动力学与结构的协同重整化:现有方法多关注静态拓扑,而实际网络(如神经活动、舆论传播)的动力学粗粒化需与结构变换耦合。
3. 广义临界性(Generalized Criticality):异质性和长程连接可能导致多重相变或扩展的Griffiths相(Griffiths Phase),需重新定义临界指数(Critical Exponents)。
4. 信息几何与参数流:通过Fisher信息矩阵(Fisher Information Matrix)识别“相关参数”,构建数据驱动的重整化框架,已在化学网络和神经网络中初见成效。
复杂网络的重整化标志着统计物理与数据科学的深度交叉。从双曲嵌入的几何直观,到拉普拉斯谱的动力学本质,再到多尺度随机图的聚合不变性,这些方法为解析社交、生物、技术网络的普适规律提供了新范式。未来,结合信息论、机器学习与非平衡物理的跨学科工具,或将催生一套“网络场论”,统一描述从微观互动到宏观涌现的跨尺度规律。
彭晨 | 编译
复杂网络动力学读书会
6. 加入集智,一起复杂!










